Волков В.Я. и др. Курс начертательной геометрии на основе геометрического моделирования

Подождите немного. Документ загружается.

Федеральное агентство по образованию

Сибирская государственная автомобильно-дорожная академия

(СибЛДИ)

В.Я. Волков, В.Ю. Юрков, K.JI. Панчук,

Н.В. Кайгородцева

КУРС НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

НА ОСНОВЕ ГЕОМЕТРИЧЕСКОГО

МОДЕЛИРОВАНИЯ

Учебник

Допущено Научно-методическим советом по начертательной

геометрии, инженерной и компьютерной графике Минобрнауки РФ

в качестве учебного пособия для аспирантов, магистрантов и

студентов вузов инженерно—технических специальностей

Омск

Издательство СибАДИ

2010

УДК 514.18(075)

ББК 22.151 _3я73

К 93

Рецензенты:

Доктор технических наук, профессор, заслуженный

деятель науки Российской Федерации, Г.С. Пианов

(Московский государственный упниерситет леса);

Доктор технических наук, профессор, М.Д. Вертинская

(Иркутский государственный технический университет)

Работа создана на основе аналитической программы "Развитие научного

потенциала высшей школы (2009 2010 годы)"; мероприятие 2 "Проведение фун-

даментальных исследований и области естественных, технических и гуманитар-

ных паук. Научно методическое обеспечение развития инфраструктуры вузов-

ской науки"; проект "Синтетическое моделирование технических изделий и мно-

гокомпонентных, многофак торных процессов".

К 93

Курс

пачерчUICIMIOH

геометрии

на

основе геометрического моделирова-

ния: хчебннк ' В.Я. Волкон, В.Ю. Юрков, К.Л. Панчук, Н.В. Кайгородцсва. -

Омск: Изд-но С'ибЛДИ. 20)0. 253 с,

ISKN 47S-5

>05174-01-8

Киша возникла ш лекционных курсов, прочитанных авторами в универси-

тетах юрода Омска и содержавших основы современной начертательной гео-

метрии. Она охватываем почти все традиционные разделы начертательной гео-

метрии, но imaiaci их е более общей точки зрения.

Киша расечныма на студентов университетов, магистрантов, аспирантов, а

также на мрепо тншелей начертательной геометрии и научных работников в

смежных облас nix.

1абл. 3. Мл.

liiiOjiHoip.'.

назв.

ISBN 978-5-905I7-1-OI-8

.10. Юрков, К.Л. Панчук,

ВВЕДЕНИЕ

Предлагаемая книга предназначена служить пособием по курсу

начертательной геометрии. Задача, которую она должна решать, со-

стоит в том, чтобы в наибольшей степени приблизить курс начерта-

тельной геометрии к курсу высшей математики и её разделам. Авторы

исходили из следующего методического положения: доступно, мак-

симально наглядно, конструктивно, на достаточно хорошем научном

уровне изложить основные разделы начертательной геометрии, необ-

ходимые студентам, магистрантам, аспирантам университетов, пре-

подавателям вузов и инженерно-техническим работникам, желающим

повысить свои знания в области начертательной геометрии. Авторы

считают начертательную геометрию разделом математики, изу-

чающим теорию конструктивных методов отображения про-

странств различной конечной размерности и различной структу-

ры друг на друга.

Написанием этой книги авторы выражают свою озабоченность

проявившейся в последнее время тенденцией принижать значение ма-

тематических основ и конструктивных методов начертательной гео-

метрии и усиливающимся стремлением подменить изучение геомет-

рии как математической науки изучением компьютерных реализаций

частных методов начертательной геометрии. Поэтому эта книга явля-

ется, прежде всего, учебником, с помощью которого студенты, маги-

странты, аспиранты и преподаватели должны иметь возможность оз-

накомиться с основными принципиальными вопросами и спецификой

теории и методов начертательной геометрии.

Авторы не видят принципиальных трудностей и препятствий для

изложения методов построения конструктивных моделей конечно-

мерных линейных пространств, и поэтому не стали ограничивать ма-

териал учебника только моделью Монжа трехмерного пространства.

Естественно связывать наглядные представления с моделями одно-

мерных, двумерных и трехмерных пространств. Но такой подход к

теории начертательной геометрии, излагаемый в многочисленных,

издающихся в настоящее время, пособиях, на взгляд авторов, являет-

ся устаревшим. Теория построения конструктивных моделей, обоб-

щающих модель Монжа, сохраняет свой геометрический характер

при переходе к многомерным (конечномерным) пространствам. Авто-

ры стремились подчеркнуть тесную связь теории множеств, линейной

алгебры, аналитической и дифференциальной геометрий, некоторых

разделов алгебраической геометрии и конструктивной (начертатель-

ной) геометрии.

С этой целью некоторые главы книги содержат более глубокий и

широкий материал, по сравнению с традиционными учебниками.

Особое внимание в книге уделено конструктивной теории плоских и

пространственных кривых. В имеющихся учебниках но начертатель-

ной геометрии этому вопросу уделяется очень мало внимания. Тради-

ционно считается, что теория кривых второго порядка - это предмет

изучения аналитической геометрии, теория плоских и пространствен-

ных кривых высшего порядка предмет изучения алгебраической

геометрии, изучение дифференциальных окрестностей кривых -

предмет изучения дифференциальной геометрии. Поэтому, в лучшем

случае, в курсах начертательной геометрии излагаются некоторые

общие проекционные свойства кривых линий, что явно не удовлетво-

ряет современным требованиям к высшему образованию. Кроме того,

теория кривых играет огромную роль в приложениях геометрии, на-

пример, н вычислительной геометрии при проектировании различных

технических объектов, в кинематической геометрии при разработке

плоских и пространственных схем различных кинематических меха-

низмов и других приложениях.

Такой раздел, как теория поверхностей изложена в книге, наобо-

poi, очень кратко. Это объясняется отсутствием достаточно полной

теоретической основы построения конструктивных моделей поверх-

ностей. Поэтому авторы принципиально отказались от описания кон-

сфуктивных свойств таких элементарных поверхностей, как поверх-

ности второго порядка, полагая, что они достаточно полно описыва-

ются в традиционных курсах аналитической и начертательной гео-

метрии. В предлагаемой книге поверхности рассматриваются как од-

номерные множества линий, определенные необходимым множест-

вом условий.

В книге достаточно подробно рассмотрена тема "Позиционные

ыдачи". В отличие от традиционного изложения этой темы авторами

предлагается единый подход к ее конструктивному рассмотрению,

основанный на теоретико-множественном представлении множества

пересечения в евклидовом пространстве. Известные в учебной, мето-

дической и научно-методической литературе методы решения пози-

ционных задач укладываются в логическую схему того или иного

конструктивного алгоритма, вытекающего из предложенного в учеб-

нике общего подхода.

Изложение некоторых вопросов носит информативный характер

и имеет целью привлечь внимание читателей к этим вопросам, ука-

зать на возможность их применения, дать стимул к дальнейшему изу-

чению. К таким вопросам относятся, например, анализ и синтез гео-

метрических условий при построении моделей конечномерного гео-

метрического множества, теория построения конструктивных моде-

лей конечномерных аффинных и проективных пространств, связь

дифференциальных и конструктивных инвариантов кривых и поверх-

ностей, теория построения аналитических моделей линейчатых и

циклических поверхностей и гиперповерхностей.

Развитие теории и методов начертательной геометрии, как разде-

ла математики, авторы видят в создании двух различных курсов -

курса элементарной начертательной геометрии, включающего в

себя те разделы, которые в настоящее время принято относить к на-

чертательной геометрии, и курса высшей начертательной геомет-

рии, некоторые элементы которого нашли своё отражение в этой кни-

ге.

'Авторы несут коллективную ответственность за книгу и хотят

указать, что каждый из них в большей или меньшей степени прини-

мал участие при написании каждой ее главы.

ГЛАВА 1. ЭЛЕМЕНТЫ ГЕОМЕТРИИ

ЕВКЛИДОВА ПРОСТРАНСТВА

1.1. Множества (основные понятии)

Под множеством понимается объединение по какому-либо при-

знаку в единое целое совокупности объектов произвольной природы.

Объединенные объекты называются элементами множеств. Если эле-

ментами множеств являются точки, прямые или кривые линии, плос-

кости или поверхности, гиперплоскости или гиперповерхности, то

есть объекты, изучаемые в геометрии, то такие множества называют-

ся геометрическими. Поскольку мы будем рассматривать только гео-

метрические множества, то для удобства будем впредь называть их

просто множествами. Множество может быть конечным, если число-

его элементов конечно, то есть может быть задано натуральным чис-

лом, или бесконечным, если число его элементов бесконечно, то есть

не может быть посчитано. Множество, не содержащее ни одного эле-

мента, называется пустым и обозначается знаком 0 Если А - неко-

торое множество и Р - некоторое утверждение, то запись {.т t А : Р}

означает: множество элементов из А , для которых справедливо ут-

верждение Р. Например, множество А = \(х,у) е R

:х~ + у' < 4}

представляет собой совокупность всех точек (х,у), принадлежащих

закрытому кругу радиуса 2 с центром в начале системы декартовых

координат числовой плоскости R

. Различают множества дискретные,

например, множество точек числовой прямой, соответствующие це-

лым числам, и множества непрерывные, например, множество точек

той же прямой, соответствующие действительным числам. В послед-

нем случае действительное число является параметром непрерывного

множества точек прямой. Непрерывности множества значений пара-

метра соответствует непрерывность множества точек прямой и на-

оборот. Параметром непрерывного множества называется действи-

тельное число а или наборы действительных чисел (а,,о,,...,а

служащие для выделения элемента множества. Если каждый элемент

множества Л принадлежит множеству 5, то А является подмноже-

ством множества В .

Геометрическое пространство представляет собой множество с

элементами, между которыми действует определенная структура от-

ношений (система аксиом). Та или иная структура отношений опре-

деляст ту или иную геометрию данного пространства. Например, евк-

лидову, аффинную, проективную геометрии [1, 10, 37]. В последую-

щем изложении понятия "геометрическое пространство" и просто

"пространство" будем считать тождественными. Если элементом про-

странства является точка, то пространство называется точечным, если

прямая, то - линейчатым. Важной числовой характеристикой геомет-

рических множеств является размерность, то есть число независимых

параметров, выделяющих элемент из множества элементов.

Над множеством могут быть выполнены различные операции

[30J: объединение, разность, пересечение, декартово произведение,

разбиение на подмножества, расширение [31] и др.

Декартовым произведением двух множеств называется множест-

во элементов, составленных из всех пар элементов, по одному при-

надлежащих разным исходным множествам, то есть АхВ-

- {{а,Ь):а е A,b е В}. В общем случае АхВ^ВхА. Декарто-

во произведение множеств точек координатных осей X и У

составляет множество точек евклидовой плоскости:

X х Y = {{х, у): х, у е] - =о,+оо[}.

Для множества X можно выполнить операцию разбиения:

XIX; = {X, : X, *0, Х;Г\Х, = 0, \JX, = X). При этом подмножест-

ва Х

,Х

,...,Х

есть непересекающиеся классы разбиения, например,

пучок концентрических окружностей в евклидовой плоскости.

Линейным расширением двух различных точек х и у будет пря-

мая, содержащая эти точки [31], что обозначается символом <х,у>.

Линейным расширением двух множеств X и У является объединение

линейных расширений всевозможных пар точек (х,у), то есть

< X, У >= < Xj, y

>, x

• е X, у,: е У. С помощью операции линейного

расширения можно подойти к понятию линейных множеств [31].

Множество считается линейным, если с любыми своими двумя точ-

ками оно содержит прямую, через них проходящую. Точка считается

нульмерным линейным множеством, прямая - одномерным линей-

ным, плоскость - двумерным линейным, пространство Е

- трехмер-

ным линейным множеством, пространство Е„ - «-мерным линейным

множеством. Таким образом, множество считается линейным, если

оно совпадает со своим линейным расширением, то есть X =< X >.

Если оно не совпадает со своим линейным расширением, то оно счи-

тается нелинейным. Кривая линия — одномерное, поверхность — дву-

мерное нелинейные множества.

множество Y. Элемент у = F(x) называется образом элемента х. а х

- прообразом элемента у в отображении F.

Рассмотрим частные случаи отображения. Если х

Ф х

F(x,) Ф F(x

) для Ух

g X , то F называется взаимно однозначным

отображением А" в Y или инъекцией (разным прообразом соответст-

вуют разные образы).

Пусть F(X) - образ множества X в отображении F. Если

F(X)-Y, то называется сюръекцией (все множество прообразов

отображается на все множество образов).

Если отображение одновременно инъективно и сюръективно, то

оно называется взамнооднозначным отображением множества А' на

множество Y или биекцией. Множества X и Y в этом случае назы-

ваются эквивалентными.

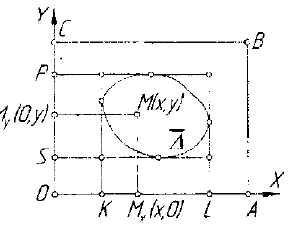
Рассмотрим пример. Пусть зада-

ны окружность к и прямая Ь, прохо-

дящая через ее центр О (рис. 1.2).

Установим соответствие между ок-

ружностью к и прямой b проециро-

ванием по направлению прямой а.

Очевидно, \ckxb и А есть график

соответствия -- (A,k,h), устанавли-

ваемого проецированием в направлс-

Р Рис. 1.2. Интерпретация

нии прямой а. Соответствие отображения

является отображением, поскольку

F(k) - | .ifl] с h . Это отображение не является инъекцией, так как

/'( М ) F(N ) ^ Т, то есть разным точкам М и N окружности к соот-

ветствует одна точка Т прямой Ь. Это отображение пе является

сюръекцией, поскольку F{k) - [АВ] Ф Ъ , то есть все множество точек

окружное [и А пе отображается проецированием по направлению

прямо)') с/ на всю прямую Ъ.

Рассмотрим соответствие F = {А,РМЕ,Ь) между дугой РМЕ ок-

ружности к и прямой А, где АсРМЕхЬ и А есть график соответст-

вия, устанавливаемого те же направлением проецирования. Очевидно,

соответствие РМЕ—>Ь является отображением. Это отображение

инъективно, так как при произвольных разных точках Р и М получа-

ем F(P) - К; F(M) = Т, К ФТ . Однако оно не является сюръекцией,

поскольку F(PME~) = \КЕ\ Ф Ь.

Для биективного отображения F существует отображение F~

обратное к F: F' \у) = х. Если в отображении имеет место F(x) = х,

то х называется инвариантным элементом отображения. Если для

подмножества Х\ с X выполняется F{X

{

) = Х

, то подмножество Х

инвариантно в отображении F. Для первого вышерассмотренного

примера точки L и Е являются инвариантными, для второго - точка

Е. Известны свойства отображений [30], из которых отметим ниже-

следующие.

1. Для любых двух подмножеств Х

и Х

множества X образ

пересечения содержится в пересечении их образов, то есть

F(X

л!,)с Е(Х

)(Л F{X

)• Образ пересечения в общем случае не

равен пересечению образов.

2. Для любых двух подмножеств Y

и У

множества Y прообраз

пересечения равен пересечению их прообразов, то есть

F '(Г, nY

) = F '(^)nF-4K

Преобразованием множества X Ф 0 называется всякая биекция

F этого множества на себя: Х-*Х. При этом всякое подмножество

а X переходит в некоторое подмножество Х

с X, то есть

F(X

) - Х

. Элемент х е X или подмножество Х

cr X называются

инвариантным элементом F(x) = х или инвариантным подмножест-

вом F(X

]

) = X

в преобразовании F.

Декартово

произведение

Соответ-

ствие

Функция >

Отобра-

жение

Инъсюшя

Сюр-ьекция

Биекция

Преобра-

зование

Рис. 1.3. Виды соответствий

Применение различных видов преобразований плоскости и про-

странства приводит к различным решениям задач начертательной

геометрии и к упрощению этих решений [15, 16, 22, 36].

Последовательное образование различных видов соответствий

между двумя множествами можно представить схематично следую-

щим образом (рис. 1.3).

1.3. Операция проецирования

Пусть <2" - множество, элементу а которого соответствует набор

п параметров (a

,—,a

). Пусть, например, а„ =-t, где / -фиксиро-

вание число. Тогда во множестве Q

выделяется подмножество Ф"~

]

элемент которого определяется набором из п-\ параметров. Напри-

мер, в пространстве i?

каждая точка определена тройкой чисел

(х,у,г), я если z - t, то Ф

есть плоскость, каждая точка которой оп-

ределяется набором из двух параметров. Существует непрерывное

однопараметрическое множество изменяющихся значений параметра

а„, а, следовательно, и непрерывное однопараметрическое множество

(и-I)-мерных подмножеств, каждому из которых соответствует оп-

ределенное значение этого параметра. При этом никакие два подмно-

жества не пересекаются, и объединение всех подмножеств есть мно-

жество Q". Эти подмножества представляют собой классы эквива-

лентности. Два элемента a cz Q" и Ь с Q" с соответствующими набо-

рами (а-

,а

,—,а„) и (b

]

,...Ji

) будут принадлежать некоторому

подмножеству Ф"~' множества Q*

, если a

=t, где / - фиксиро-

ванное действительное число. Можно показать, что введенное таким

образом условие инцидентности элементов одному (и - 1)-мерному

подмножеству есть отношение эквивалентности, а само подмножест-

во - (н U-мсрпый класс эквивалентности.

F.CJIH фиксируются два параметра из набора (а

1ь

,...,а

), то из

{У

выделяется подмножество Ф"

. При непрерывном изменении

значений этих двух параметров получаем непрерывное двухпарамет-

рическое множество (л-2)—мерных подмножеств - классов эквива-

лент нос ги, попарно не пересекающихся и заполняющих все множест-

во Q". Обобщая рассуждения, приходим к выводу, что при фиксиро-

вании т параметров из набора (а

1я

,а

) множество Q

разбива-

ется на т -параметрическое множество классов, в каждом из которых

содержится (п — т)--параметрическое множество элементов. Имеет

место тождество т + {п -т)-п. Обозначив (п~т) = 1, приходим к

следующей условной записи, разбиения множества Q

на классы эк-

вивалентности: Q

=ф

т(1

\(jn + /) = «, где Ф"^ - фактормножество

размерности т, состоящее из классов эквивалентности ф', каждый из

которых представляет собой /-параметрическое множество элемен-

тов. Таким образом, можно записать: Q" - ф

^ = [}<р'.

Основываясь на вышеизложенном, рассмотрим сущность опера-

ции проецирования. Между множествами X и Y пространства Е„

можно установить различные соответствия, сопоставляя с элементом

х € X один или несколько элементов

у е Y (рис. 1.4). Сопоставление элементов

может быть выполнено конструктивно.

Для этого необходимо выполнить разбие-

ние пространства Е

на классы эквива-

лентности: Е

=ф'"

(/)

=[J(p

^ т + 1 — п и

Рис. 1.4. Операция

проецирования

отнести образ у и прообраз х к одному

классу эквивалентности q), который на-

зовем проецирующим классом. При вы-

боре способа проецирования, то есть раз-

биения пространства Е„ на проецирую-

щие классы, необходимо учитывать ни-

жеследующее.

1. Через каждый элемент должен проходить один класс (fi.

2. Элементы пространства, через которые проходит множество

классов ф, либо не существуют, либо составляют некоторое множе-

ство ,к=0,\,2,...;к <п, которое исключается из операции нахож-

дения соответственных элементов. Класс ц/

, если он есть, называется

центром или ядром проецирования.

Приведем примеры разбиения пространства Е

на проецирующие

классы. Фактормножествами пространства Е

по отношению эквива-

лентности, представляющем собой разбиение этого пространства на

проецирующие классы, могут быть: Е

=ф"

)

= {J<p

- двухпарамет-

рические множества линий и Е

~ф

^ ~{}(р

- однопараметриче-

ские множества поверхностей. Рассмотрим вначале примеры проеци-

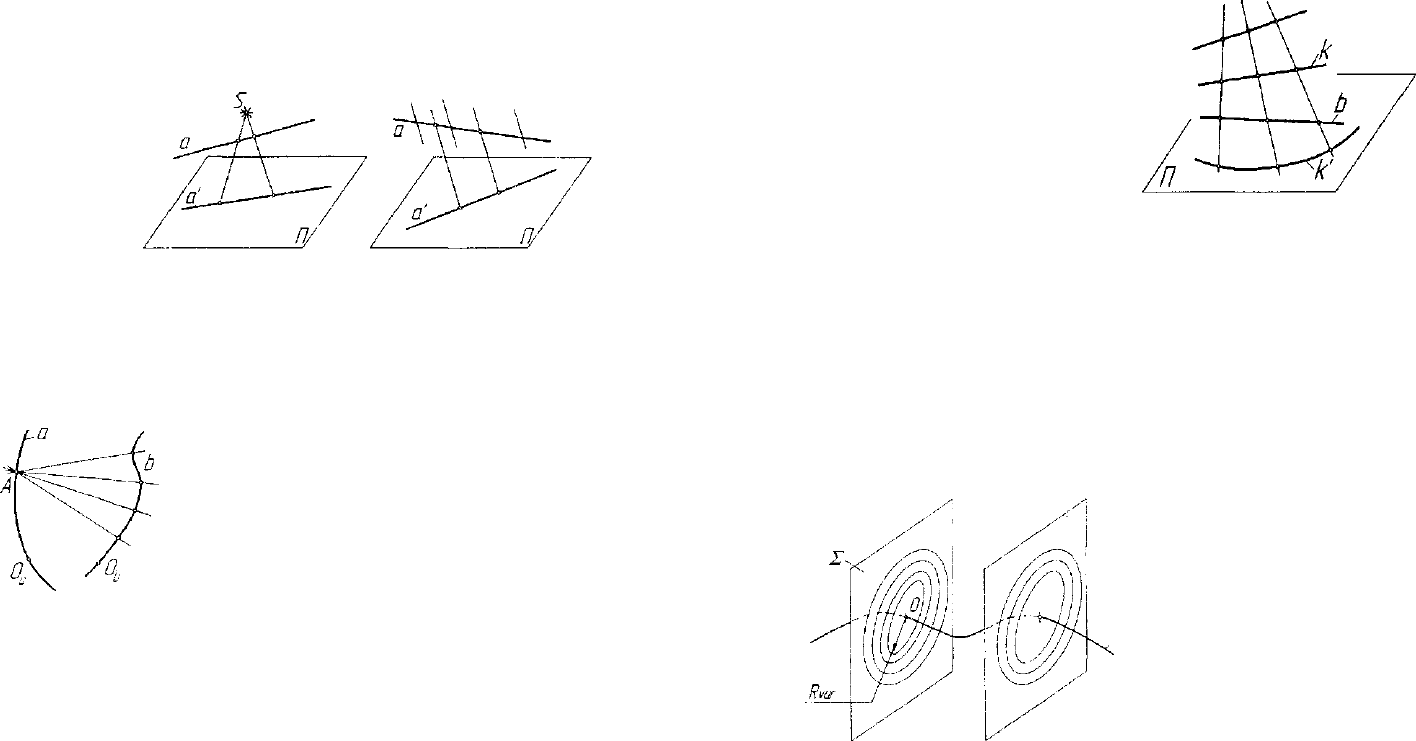
Рис. 1.5. Связка с

собственным центром

Рис. 1.6. Связка с

несобственным центром

рующих фактормножеств [j(p . Очевидно, что эти фактормножества

представляют собой множества прямых или кривых линий (плоских

или пространственных). К ним относятся известные в начертательной

геометрии нижеследующие множества.

1. Связка прямых с собственным 5 (рис. 1.5) или несобствен-

ным (рис. 1.6) центром - ядром проецирования. В обоих случаях

связка проецирующих прямых позволяет выполнить линейное ото-

бражение - про-

ецирование про-

странства Е

на

плоскость проек-

ций П, при кото-

ром проекцией

прямой а про-

странства является

прямая а' в плос-

кости проекций.

Связка прямых представляет собой конгруэнцию первого порядка

(число прямых конгруэнции, проходящих через точку пространства) и

нулевого класса (число прямых конгруэнции, принадлежащих плос-

кости пространства). Она обозначается как Ах (1,0).

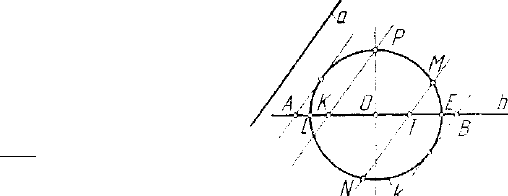
2. Кож руэнция прямых, как множество

прямых линий, пересекающих две заданные

кривые линии а и Ъ, называемые фокаль-

ными линиями (рис. 1.7). Это множество

двухпараметрично. Действительно. Поло-

жение точки А на линии определяется од-

ним параметром, например расстоянием от

некоторой фиксированной точки О

е а,

измеренным по линии а. Через точку Аеа

проходит однопарамстрическос множество

прямых, пересекающих линию b (коническая поверхность {А,Ь)) и

положение каждой прямой этого множества определяется положени-

ем ее точки пересечения с линией Ъ, определяемым расстоянием от

некоторой точки O

eb, измеренным по линии Ь. Таким образом,

множество прямых рассматриваемой конгруэнции двухпараметрично.

В начертательной геометрии для проецирования чаще всего исполь-

зуются конгруэнции прямых, фокальными линиями которых являют-

Рис. 1.7. Кош руэнция

прямых

ся прямые а и Ъ. В этом случае образуется Кг (1.1) (рис. 1.8). Мно-

жество прямых этой конгруэнции обеспечивает нелинейное проеци-

рование, у которого прямые линии а и Ъ — ядро проецирования.

Нелинейность можно объяснить сле-

странства Я

на плоскость является

квадратичным. Оно обеспечивается двупараметрическим множеством

классов эквивалентности — проецирующими линиями конгруэнции с

исключенным ядром проецирования - фокальными линиями а и b.

Очевидно, что использование в качестве проецирующих классов

(/) прямых линий недостаточно для получения линейного отображе-

ния, при котором прямая линия пространства отображается в прямую

линию плоскости проекций. Необходимо, чтобы само фактормноже-

ство Ф

2(П

= Uq>

]

, объединяющее эти классы, было линейным. В рас-

дующим образом. Задание прямой к

пространства при заданных фокаль-

ных линиях а и b конгруэнции при-

водит к образованию линейчатой по-

верхности — однополостного гипер-

болоида (а,Ь,к). Сечение этой по-

верхности плоскостью проекций П

представляет собой кривую к' вто-

рого порядка. Следовательно, рас-

сматриваемое отображение про-

Рис. 1.8. Проецирующая

конгруэнция Кг (1,1)

смотренном примере использо-

вания Кг (1,0) оно линейно, а в

примере с Кг (1,1)

нелинейно

(квадратично). Очевидно, так-

же, что для обеспечения про-

хождения, через каждую точку

,о пространства единственного

проецирующего класса (/} ~

Рис. 1.9. Циклическая

конгруэнция

прямой линии, необходимо ис-

пользование конгруэнции пер-

вого порядка.

Рассмотрим примеры ис-

пользования в качестве проеци-

рующего фактормножества Ф —\J<p двухнараметрические множе-

ства кривых линий.

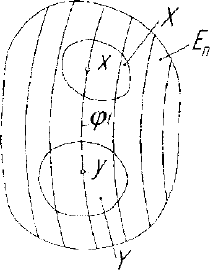
1. Циклическая конгруэнция с плоскостью параллелизма (рис.

1.9). Она представляет собой двухпараметрическое множество ок-

ружностей в пучке параллельных плоскостей и с центрами окружно-

стей на линии а, которая в частности может быть прямой. Каждой

плоскости Е этого пучка принадлежит пучок (0) концентрических

окружностей. Если плоскости пучка перпендикулярны линии а, то

циклическая конгруэнция называется нормальной. Линия а линия

центров окружностей, исключена из проецирования. Использование

циклической контруэнции в качестве проецирующего фактормноже-

ства приводит к нелинейному проецированию. Вели а - прямая ли-

ния, то прямая Ъ пространства отображается проецированием на

плоскость проекций в кривую второго порядка, поскольку является

сечением однополостного гиперболоида вращения (а,Ь) с осью вра-

щения а.

2. Винтовая конгруэнция (рис. 1.10). Может представлять собой

двухпараметрическое множество соосных цилиндрических винтовых

линий постоянного винтового шага h и одного направления. Винто-

вой проекцией прямой линии Ъ пространства на плоскость проекций

будет кривая линия, представляющая собой сечение геликоида

(a,h,h) плоскостью проекций. Линия а - ось винтовой конгруэнции,

исключена из проецирования.

Рис. 1.1(1. Винтовая Рис. 1.11. Нормальная

конгруэнция конгруэнция

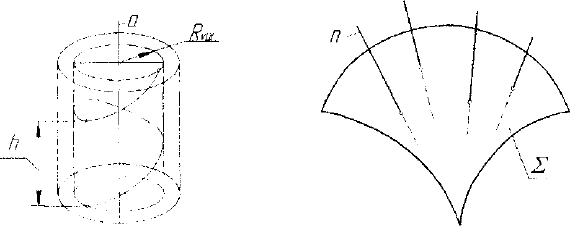
3. Нормальная конгруэнция (рис. 1.11). Представляет собой

двухпараметрическое множество нормалей некоторой поверхно-

сти Е. Отображение объектов пространства £

может быть выпол-

нено как на саму поверхность 27 (поверхность проекций), так и на

плоскость пространства (плоскость проекций). Очевидно, отображе-

ние пространства нормальной конгруэнцией является нелинейным.

В качестве проецирующего фактормножества = \}<р

могут

быть использованы: пучок плоскостей с собственной или несобствен-

ной осью, пучок сфер - концентрических или эксцентрических (если

координаты центра и радиус сферы связаны какой-либо зависимо-

стью), пучок соосных цилиндрических поверхностей вращения, пучок

соосных круговых конических поверхностей с общей или разными

вершинами и другие множества поверхностей.

1.4. Аксиоматическое построение евклидова пространства

Основным элементом евклидова пространства является точка -

неопределяемый геометрический объект, если не считать определе-

ния, данного Евклидом (330 - 275 г.г. до н.э.), что "точка есть то, что

не имеет частей". Формально, точку можно считать нульмерным про-

странством Е

. Чтобы определить одномерное пространство Е

, необ-

ходимо иметь прямую, существование которой задается первой ак-

сиомой принадлежности, выбрать на ней любую точку, которую при-

нимаем за начало отсчета, тогда любая точка прямой определится за-

данием одного числа (координаты), которое является выражением

расстояния данной точки от начала координат. Таким образом, одно-

мерное пространство Ь\ линейно по определению и эквивалентно ли-

нейному однопараметрическому множеству точек.

Двумерное пространство Е

есть плоскость, существование кото-

рой определяется четвертой аксиомой принадлежности. Поскольку

аксиомы определяют существование трех точек, принадлежащих Е

то одну из них всегда можно принять за начало отсчета координат, а

две другие точки зададут две оси координат, не обязательно между

собой перпендикулярные. Любая точка А е Е

определяется двумя

числами - координатами (х,у) = (х

,х

), геометрический смысл кото-

рых заключается в длинах отрезков, отсекаемых на соответствующих

координатных осях от начала координат прямыми, проходящими че-

рез точку А, параллельно другой оси координат. Пространство Е

линейно по определению, и представляет собой линейное двухпара-

метрическое множество точек. Очевидно, что обобщение этих рассу-

ждений приведет к пространствам Е

, £

, Е

Поэтому группа аксиом принадлежности единственным образом

расширяется от:

1) для любых грех точек, не лежащих на одной и той же прямой,

существует плоскость и притом только одна, прохо;гящая через эти

точки;

2) если две точки прямой лежат в плоскости, то всякая точка

этой прямой лежит в этой плоскости;

3) если две плоскости имеют общую точку, то они имеют еще

одну общую точку;

до:

1) для любых (к + 2) точек, не лежащих в одном и том же про-

странстве Е

, существует пространство Е

к+Х

и притом только одно,

проходящее через эти точки;

2) если (к+ 2) точек пространства Е

лежат в Е

кп

, то всякая

точка пространства Е

лежит в Е

к+]

;

3) если два пространства Е

, лежащих в E

itl

, имеют общую

точку, то они имеют, по крайней мерс, еще (к -1) общую точку.

Естественно, что для к > 3 получаются абстрактные евклидовы

пространства, для которых Е~, а Е

cz ... а Е

а ... cz Е

. Поскольку

эти пространства — линейные, то они называются соответственно 0-

плоскостью (точка), 1-плоскостью (прямая), 2-плоскостью, к-

плоскостью. (/7-1)-плоскость называется гиперплоскостью.

В Е

можно ввести координаты. Поскольку аксиомы утверждают

существование (и + 1) точек, то одну из них можно принять за начало

координат, а на остальных п точках построить координатные оси, не

обязательно перпендикулярные друг другу. Тогда между упорядочен-

ными наборами чисел (х

,...,х

) и точками пространства Е

будет ус-

тановлено взаимно однозначное соответствие. Геометрический смысл

каждого числа x

/ = 1, п будет таким же: x

выражает длину от-

резка, отсекаемого от начала координат О на числовой оси Ох

(

ги-

перплоскостью, проходящей через данную точку параллельно осталь-

ным осям координат.

На основе аксиом принадлежности пространства Е

докажем

теоремы о пересечении и линейном расширении двух подпространств

и Е . Пусть подпространства Е

с Е

и Е

а Е

определяются

соответственно (£ + 1) и (р + У) независимыми точками. Пусть

слЕ

~ 0. Тогда получим (к + р + 2) независимые точки. По ак-

сиоме принадлежности эти точки определяют (к + р + Х)—мерное под-

пространство. Следовательно, имеем теорему: для любых двух под-

пространств Е

с Е„ и Е

d Е

, для которых Е

пЕ

= 0, сущест-

вует подпространство Е

к+р+х

а Е

, которое является их линейным

расширением.

В этой теореме подразумевается, что к + р +1 < п. Предположим,

что к + р +1 >п. Тогда Е

с\Е

±- 0, то есть существует некоторое

/'-мерное подпространство Е

аЕ

, которое называется подпро-

странством пересечения пространств Е

и Е

: Е

слЕ

- E

, г <п.

Пространство Е

определяется (/" + 1) независимыми точками. Тогда

будет определяться еще к + \-г-\ = к-r независимыми точками,

а Е будет определяться р+\—г—\=р-г независимыми точками.

Поскольку общее число независимых точек не может быть больше

п +1, то имеем k-r + p-r + r + \- n + \. Или к + р = п + г. Отсюда

г — к + р — п. Следовательно, имеем теорему: для любых двух под-

пространств Е

с Е

и Е с Е

, для которых к + р + 1 > п, существу-

ет подпространство пересечения Е

а Е

, E

а Е

, размерность ко-

торого равна г = к + р — п.

1.5. Операция проецирования в пространстве Е

Рассмотрим теперь более конкретно операцию проецирования.

Для этого выберем некоторое подпространство Е

с Е

и точку

Л<£Е

. Поставим задачу отобразить точку А в точку А'е Е

одно-

значно. По теореме о пересечении подпространств точка А' должна

быть пересечением Е

и Е

, и, очевидно, что АеЕ

. Следова-

тельно, по аксиоме принадлежности Е

кроме точки А должно оп-

ределяться (п-к) точками пространства Е

. Значит, в пространстве

должно быть выбрано подпространство E

, Е

пЕ

= 0,

А £ Е

(рис.1.12). Е

называется центром или ядром операции

проецирования. Если соединить А и А' прямой АА', то АА'а Е

ААс\Е

= А". Точку А" можно рассматривать как проекцию точ-

ки А на подпространство Е

из центра Е

. Прямую АА'А" обыч- *

но называют линией связи проекций. Итак, проецирование точки на