Власов К.П., Анашкин А.С. Теория автоматического управления
Подождите немного. Документ загружается.


xbxbybxbyayayaya
mm
mm
nn
nn
1
)1(
1
)(
01
)1(
1
)(
0
. (3.8)
Умножив (3.8) на
pt
e
после интегрирования его по t в
пределах от 0 до при нулевых начальных условиях, получим это
уравнение, преобразованное по Лапласу:
)()()()(
1
1
101
1
10
pXbpbpbpbpYapapapa
mm
mm
nn
nn
.
Отсюда
)(
)(
)(
)()(
1
1
10
1
1
10
pX
pA
pB
pX
apapapa
bpbpbpb
pY
nn
nn
mm
mm
.
(3.9)
Обозначим
)()(/)( pWpApB
. Тогда (3.9) перепишется в
виде Y(p)4=4W(p)X(p), откуда
)(
)(
)(
pX
pY
pW
. (3.10)
Выражение (3.10), т.е. отношение изображения выходной
переменной системы Y(p) к изображению входной переменной X(p)
при нулевых начальных условиях, называется передаточной
функцией системы.
Поскольку при исследовании динамических свойств системы
требуется определить зависимость переменных в функции
действительного аргумента t, возникает обратная задача: как от
изображения переменной перейти к ее оригиналу.
Наиболее общим способом нахождения оригинала y(t) по
известному изображению Y(p) является применение обратного
преобразования Лапласа:
j
j
pt
dppY
j
pYLty e)(
2
1
)()(
1
. (3.11)
21

Для большинства типовых изображений обратное
преобразование Лапласа табулировано, поэтому наиболее простым
способом нахождения оригинала по изображению является
использование таблиц, в которых для наиболее распространенных
функций y(t) приведены соответствующие изображения Y(p).
Представим Y(p) дробно-рациональной функцией вида
)(
)(
)(
pA
pB
pY
,
где B(p) и A(p) – полином соответственно m-й и n-й степени,
причем;m;<;n.
Тогда оригинал y(t) находим по теореме разложения
Хевисайда – Карсона:
t
k
p
n
k
k
k
pA
pB
ty e
)(
)(
)(
1
, (3.12)
где p
k
– корни уравнения A(p)4=40;
dppdApA /)()(
.
➢;;;Приме р4 . Пусть ДУ системы имеет вид
kxyayaya
210
.
Требуется найти W(p), w(t), h(t).
Преобразуем ДУ системы по Лапласу при нулевых
начальных условиях. Получим
)()()(
21
2
0
pkXpYapapa
.
Откуда передаточная функция будет
22
w(t)
t
h(t)
t
0,5
а б
Рис.3.5

21
2
0
)(
)(
)(
apapa
k
pX
pY
pW
.
Пусть k4=41, a
0
4=41, a
1
4=43, a
2
4=42. Для нахождения функции
веса w(t) воспользуемся теоремой разложения. При этом учтем, что
L{(t)}4=41. Тогда
2
1
1
e
)(
)(
)()(
k
t
k
p
k
k
pA
pB
pWLtw
. (3.13)
Имеем A(p)4=4a
0
p
2
4+4a
1
p4+4a
2
4=4p
2
4+43p4+424=40; p
1
4=4–1;
p
2
4=4–2; A(p)4=42p4+43; B(p)4=4k4=41. Тогда, подставив B(p), A(p),
p
1
и;p
2
в выражение (3.13), получим (рис.3.5,;а)
tttt
tw
22
eee
3)2(2
1
e
3)1(2
1
)(
.
Аналогичным образом находим переходную характеристику
(рис.3.5,;б), при этом учитываем, что L{1(t)}4=41/р, тогда
A(p)4=4(p
2
4+43p4+42)р4=40; p
1
4=4–1; p
2
4=42; p
3
4=40;
A(p)4=43p
2
4+42р4+42. Воспользовавшись (3.12), найдем
tt
th
ee5,05,0)(
2
.
3.3. Частотные характеристики линейных систем
Пусть ДУ системы имеет вид
xbxbybxbyayayaya
mm
mm
nn
nn
1
)1(
1
)(
01
)1(
1
)(
0
. (3.14)
Воспользуемся прямым преобразованием Фурье, которое
можно получить из преобразования Лапласа при p4=4j:
dttfjFtf
tj
e)()()(Ф
. (3.15)
Тогда (3.14) запишется в виде
23
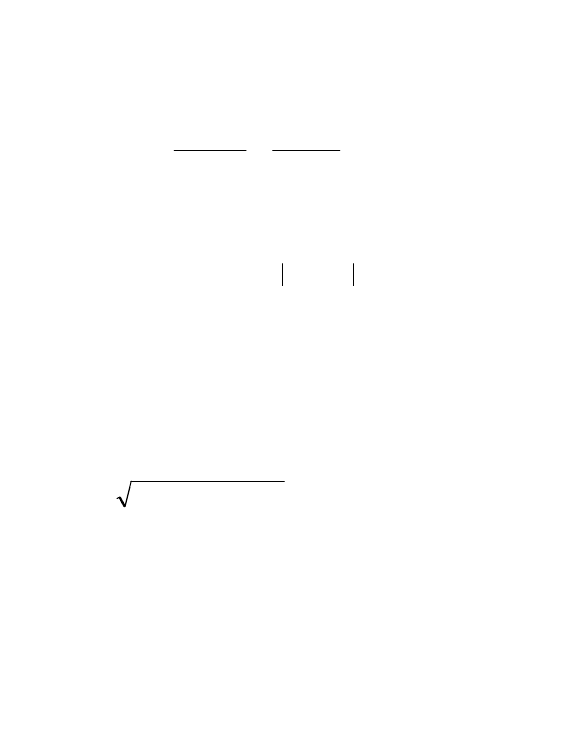
)())()((
1
1
10
jYajajaja
nn
nn
)())()((
1
1
10
jXbjbjbjb
mm
mm
.
Отсюда
)(
)(
)(
)(
)(
jW
jA
jB
jX
jY
. (3.16)
Выражение (3.16) представляет собой частотную функцию
или амплитудно-фазочастотную характеристику системы (АФЧХ),
)(arg
e)()(
jWj
jWjW
,
где W(j)4=4A() – амплитудно-частотная характеристика системы
(АЧХ), а argW(j)4=4() – фазочастотная характеристика системы
(ФЧХ).
Частотная функция системы (3.16) может быть представлена
в алгебраическом виде:
W(j)4=4A()e
j
(
)
4=4P()4+4jQ(),
где
).(/)(arctg)(;)()()(
22
PQQPA
В данном случае P() называют вещественной частотной
характеристикой, а Q() – мнимой частотной характеристикой.
Ее также можно представить в логарифмическом виде:
lgW(j);=;lgA();+;j()lge,
где lge4=40,434.
В случае подачи на вход системы гармонического сигнала
x4=4asint или
)](*Im)(;sincos[ee)(* txtxtjtatx
tjtj
, частное
решение уравнения (3.14) отыскивается в том же виде, что и
входной сигнал x(t):
y(t)4=4A
0
sin(t4+4) или y*(t)4=4A
0
e
j(
4 +4
t)
.
24

Подставив x*(t) и y*(t) в (3.14) и сократив e
j
t
, получим
A(j)A
0
e
j
4=4B(j)a,
)(
)(
)(
e
0
jW
jA
jB
a
A
j
. (3.17)
Из сопоставления уравнения (3.16) с уравнением (3.17) при
4=4const получим
25
р
А()
А(0)
0;<;;<;1
;>;1
а
2
+j
+
;=;0
1
;=;
W(j
)
n;=;4
в
Рис.3.6
()
n
2
б
n
n
a
b

)(arg;)(
0
jW
a
A
jW
.
Если – переменная величина (4=4var), то величина A
0
будет функцией частоты, тогда
),(/)(
0
AaA
где A() –
амплитудно-частотная характеристика (рис.3.6,;а), которая
характеризует усиление периодического сигнала на различных
частотах. При изменении изменяется и фаза выходного сигнала y
по отношению к входному x, т.е. имеем () – фазочастотная
характеристика (рис.3.6,;б). Здесь
р
– резонансная частота.
Геометрическое место концов вектора частотной функции на
комплексной плоскости при изменении частоты от нуля до
бесконечности называется годографом вектора W(j) (рис.3.6,;в).
Заметим, что для нахождения функции действительного
переменного t при известной функции Y(j) необходимо
воспользоваться обратным преобразованием Фурье:
djYjYty
tj
e)(
2
1
)(Ф)(
1
.
3.4. Условия однозначной связи
между частотными характеристиками
Из соотношения W(j)4=4A()e
j
(
)
4=4P()4+4jQ() следует,
что частотная характеристика полностью определена, если задана
любая из пар: A() и () или P() и Q(). Однако при
определенных условиях существует
однозначная связь между A() и (),
а;также P() и Q(). Это позволяет
упростить исследования систем,
ограничиваясь, например,
рассмотрением A() или P(). В теории
интегралов Фурье доказывается, что
условие существования однозначной
связи заключается в том, чтобы
частотная функция
26
+j
+
j
k
–
Рис.3.7
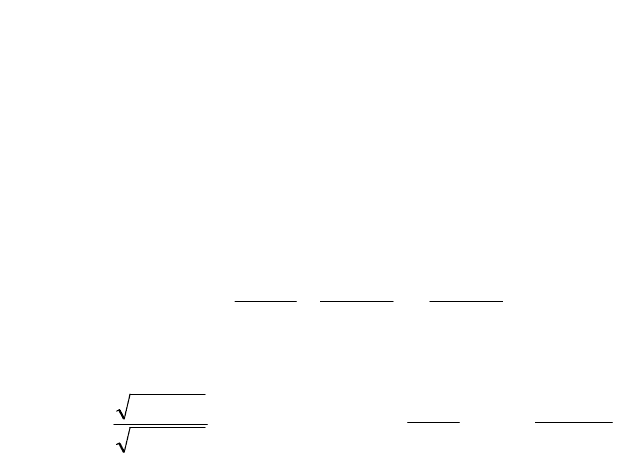
)(/)()( jAjBjW
не имела ни нулей, ни полюсов в нижней
полуплоскости корней полиномов числителя и знаменателя (нули –
корни полинома B(j)4=40, следовательно, W(j)4=40, а полюса –
корни полинома A(j)4=40, следовательно, W(j)4=4 – рис.3.7).
Системы, которые удовлетворяют этим условиям,
называются минимально фазовыми. Из всех возможных систем с
одной и той же АЧХ они дают наименьший сдвиг фаз при любой
частоте .
➢;;;Приме р5. Пусть W
1
(j)4=41 (линия передачи сигнала).
Следовательно, A
1
()4=41, а
1
()4=40. Пусть
2222
22
2
2
)(
a
a
j
a
a
aj
aj
jW
,
где a4=4const.
Тогда
1)(
22
22
2
a
a
A
;
22
2
2
arctg
)(
)(
arctg)(
a
a
P
Q
.
Поскольку корень числителя W
2
(j) лежит в нижней
полуплоскости (
1
4=4–ja), эта система принадлежит к классу
неминимально-фазовых, а
2
() отлична от нуля при ;;0 и
зависит от а.
Таким образом, системы имеют одинаковые амплитудно-
частотные характеристики A
1
()4=4A
2
()4=41, но разные фазо-
частотные. Последнее свидетельствует о неоднозначности связи
между A
2
() и
2
() и необходимости рассматривать эти
характеристики совместно.
3.5. Связь между операторами преобразования
сигналов
линейной системы
Как было сказано ранее, оператором преобразования
называется математическое выражение, связывающее входную и
выходную величины системы, т.е. y4=4A{x} (см. рис.3.1).
27

Основным оператором линейной системы является линейное
дифференциальное уравнение, в правой части которого стоит
входная величина, а в левой – выходная, например,
xbyaya
010
. (3.18)
Преобразовав уравнение (3.19) по Лапласу при нулевых
начальных условиях, найдем передаточную функцию, которая также
является оператором преобразования:
xbLyayaL
010
или
)()()(
010
pXbpYapa
,
тогда
)(
)(
)(
10
0
pX
pY
apa
b
pW
. (3.19)
Преобразовав выражение (3.18) по Фурье, получим
частотную функцию системы:
10
0
)(
)(
)(
aja
b
jX
jY
jW
. (3.20)
Сопоставив (3.19) и (3.20), найдем
jp
pWjW )()(
.
Решим ДУ (3.18) классическим методом при типовом
единичном ступенчатом возмущении x(t)4=41(t) и нулевых
начальных условиях:
t
a
a
a
b
thty
0
1
1
0
e1)()(
.
Воспользовавшись (3.19) и учтя, что
ptL /1)}(1{
,
получим:
p
pW
pXpWpHpY
)(
)()()()(
,
тогда
28

p
pW
Lth
)(
)(
1
. (3.21)
Таким образом, выражение (3.21) связывает передаточную
функцию с переходной функцией. При этом
W(p)4=4pL{h(t)}4=4pH(p).
Весовую функцию w(t) находим с учетом того, что
x(t)4=4(t)4=41(t). Так как w(t)4=4h(t), то
t
a
a
abtw
0
1
00
e)/()(
.
Воспользовавшись (3.19) и учтя, что L{(t)}4=41, получим
Y(p)4=4W(p)4=4L{w(t)}, (3.22)
тогда
w(t)4=4L
-1
{W(p)}.
4. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ АСУ
Современные АСУ состоят из элементов различной
физической природы, конструктивного исполнения, источников
энергии и т.д. Динамические свойства этих элементов часто можно
описать одним и тем же ДУ. Положив в основу классификации
динамические свойства, обычно выделяют следующие звенья:
усилительное, инерционные, колебательное, интегрирующее,
дифференцирующее.
1.;Усилительное звено. Оператор преобразования равен k:
y4=4kx.
2.;Инерционные (апериодические) звенья первого порядка,
описывается ДУ вида:
kxyyT
; второго порядка –
kxyyTyT
ξ2
2
при ;>;1, корни характеристического
уравнения вещественные отрицательные.
3.;Колебательное звено (0;<;;<;1) –
kxyyTyT
ξ2
2
при;0;<;;<;1, корни характеристического уравнения комплексные
сопряженные.
В статическом режиме (при равенстве нулю всех
производных) все приведенные звенья имеют уравнение,
аналогичное усилительному звену, что свидетельствует о наличии
связи между входной величиной x и выходной величиной y в
29

статике. Поэтому все рассмотренные звенья относятся к классу
статических.
4.;Интегрирующее звено. Описывается выражением
t
xdtky
0
или
kxy
.
Здесь выходная величина y будет изменяться до тех пор, пока x4;0.
5.;Дифференцирующее звено –
dtkdxxky /
.
Последние два звена не имеют связи между входными
и;выходными величинами в статике, поэтому относятся к классу
астатических.
Реальные звенья можно описать уравнением и выше второго
порядка, но формально это описание можно заменить системой
уравнений, каждое из которых имеет порядок не выше второго,
и;таким образом, представить реальное звено в виде звеньев 1-5.
Поэтому эти звенья называются элементарными или типовыми.
Предполагается, что все звенья являются звеньями
направленного действия (т.е. выходная величина не оказывает
влияния на входную). Каждое звено характеризуется уравнением
динамики, передаточными функциями, частотными функциями,
временными характеристиками.
4.1. Усилительное звено
Уравнение динамики (статики)
y;=;kx или Y(p);=;kX(p).
Передаточная функция
k
pX
pY
pW
)(
)(
)(
.
Частотные характеристики: АФЧХ – W(j)4=4k; АЧХ –
A()4=4k; ФЧХ – ()4=40 (рис.4.1, а, б, в).
30
