Вайнштейн Р.А. Математические модели элементов электроэнергетических систем в расчетах установившихся режимов и переходных процессов
Подождите немного. Документ загружается.


81
Как видно из (2.1.55), Е
q
пропорциональна току возбуждения. С
учетом (2.1.55) выражение (2.1.54) можно представить в виде
q q d d
U E I x
. (2.1.56)
Преобразования по оси «q». При принятых условиях по «q» учи-
тывается только контур обмотки статора.
Подставим (2.1.31) в (2.1.18
)
d q q q q
U I L I x
. (2.1.57)
где
q q
x L
– синхронное реактивное сопротивление по поперечной
оси.
Для составляющих в выражениях (2.1.56) и (2.1.57) выполним пе-
реход от координат
d, q к фазным координатам.
Например, для тока фазы А
0 0
cos( ) sin( )
A d q
i I t I t
.
Очевидно, что теперь возможно применение символического мето-
да и представление выражений (2.1.56) и (2
.1.57) в векторной форме.
При этом, чтобы сохранить направление составляющих в (2.1.56) по оси
q, а в (2.1.57) по оси d, нужно применить оператор поворота на 90
0
, как
это принято при записи комплексных чисел
q q d d
U E I jx
,
d q q
U I jx
.
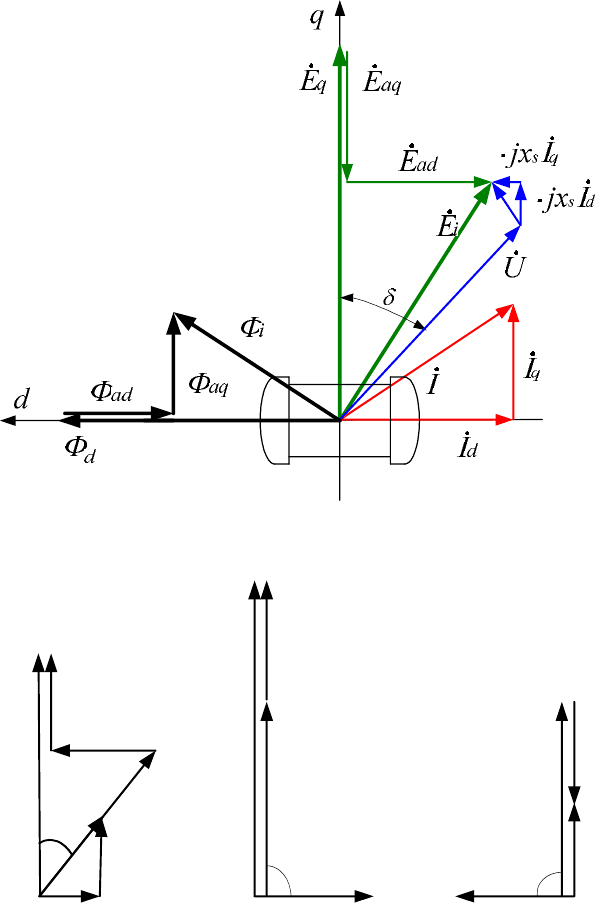
На рис. 2.1.16 показана векторная диаграмма синхронной машины
при определенной нагрузке. На рис. 2.1.16 обозначено:
Ф
d
– магнитный поток, создаваемый током возбуждения в режиме холо-
стого хода,
Ф
аd
– магнитный поток реакции статора,
Ф
аq
– магнитный поток поперечной реакции якоря,
Ф
i
– результирующий магнитный поток в воздушном зазоре генератора,
Е
q
– ЭДС холостого хода,
Е
аq
– ЭДС продольной реакции якоря,
Е
аd
– ЭДС поперечной реакции якоря,
Е
i
– внутренняя ЭДС генератора,
I, U – обобщенные векторы тока статора и напряжения генератора,
I
d
, I
q
– продольная и поперечная составляющие тока статора,
х
s
– сопротивление рассеяния.
82
Рис. 2.1.16. Векторная диаграмма синхронной машины при нагрузке
q
U U
d
I I
0
90
0
90
U
I
d d
jх I
q q
jх I
q
Е
d
I
q
I
d
I I
q
Е
q
Е
q
U U
d d
jх I
d d
jх I
а б в
Рис. 2.1.17. Векторные диаграммы при различном характере нагрузки
а – активная нагрузка,
б – индуктивная нагрузка,
в – емкостная нагрузка
Для установившихся режимов машины векторные диаграммы
обычно строятся лишь для ЭДС, токов и напряжений. На рис. 2.1.17
представлены такие векторные диаграммы для различных случаев на-
грузки генератора.
Можно несколько изменить векторную диаграмму синхронного ге-
нератора. Разлагая падение напряжения в индуктивном сопротивлении

83
рассеяния на две составляющие, соответственно продольной и попереч-
ной составляющим тока, можно падение напряжения в машине предста-
вить как геометрическую сумму падений напряжения от продольной и
поперечной составляющих тока (рис. 2.1.
18).
d
Iq
q
I
Eq
Ud
Id
Uq
U
jxad Id
jxaq Iq
jxs Id
jxs Iq
jxd Id
.
.
.
. .
.
.
.
.
.
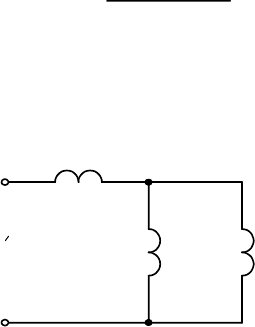
Рис. 2.1.18. Векторная диаграмма синхронной машины
в установившемся режиме
Вывод соотношений для переходной стадии процесса. Из
(2.1.30) выразим ток
f
i
f d ad
f
f
I M
i
L
. (2.1.58)
Подставим (2.1.58) в (2.1.54)
ad
q f d ad d d
f
M
U I M I L
L
.
Группируем члены, содержащие I
d
2
ad ad
q f d d
f f
M M
U I L
L L
. (2.1.59)
В (2.1.59) множитель при I
d
есть переходное реактивное сопротив-
ление, что можно показать на основе теоремы о постоянстве потокосце-

84
пления. Изменения напряжения, потокосцепления и тока при возникно-
вении какого
-либо возмущения по (2.1.59)
2
ad ad
q f d d
f f
M M
U I L
L L
. (2.1.60)
Так как потокосцепление с замкнутым контуром не может изме-
ниться скачком, то
0
f
и из (2.1.60) отношение
2
q
ad
d d
d f
U
M
x L
I L
,
где
d
x
– переходное реактивное сопротивление по продольной оси.
Первый член в выражении (2.1.59), пропорциональный потокосце-
плению обмотки возбуждения
– есть ЭДС
q
E
за переходным сопротив-
лением
ad
q f
f
M
E
L
. (2.1.61)
Выражение (2.1.59) можно представить в виде
q q d d
U E I x
. (2.1.62)
Схема замещения для
d
x
через внутренние параметры генера-
тора.
В выражении для
2
ad
d d
f
M
x L
L
учтем, что
,
d ad f ad f
L M L L M L
.
Тогда
2
2 2
( )
.
ad
d ad
ad f
ad ad f ad f ad
ad f
ad f f ad
ad f
M
x M L
M L
M L M L M L L M
M L
L M L L M
M L
85
Таким образом, окончательно
f ad
d
ad f
L M
x L
M L
. (2.1.63)
Полученной формуле (2.1.63) соответствует схема замещения на
рис. 2.1.18
x
f
x
аd
x
x
d
Рис. 2.1.18. Схема замещения для
d
x
через внутренние параметры генератора
4.2.9. Переходный процесс при КЗ на выводах генератора
(без учета демпферных контуров)
Наиболее распространенной аварией в энергосистемах является
внезапное КЗ на линии электропередачи, сопровождающееся большими
токами. Протекание этого явления во многом определяется характером
процесса в синхронных генераторах.
Длительность процесса КЗ в синхронных генераторах ограничена
временем 0,1
–0,3 с. При большей продолжительности процесса генера-
тор в большинстве случаев не смодет работать синхронно с системой
после отключения КЗ
.
Несмотря на кратковременность процесса, определение токов КЗ
в цепях статора генератора имеет важное значение. Например, знание
величины этого тока необходимо для выбора выключателей, отклю-
чающих КЗ, и трансформаторов тока, питающих цепи защиты. Вычис-
ление тока в цепи возбуждения генератора позволяет оценить надеж-
ность работы возбудителя.
Рассмотрим определение данных токов при трехфазном КЗ на вы-
водах генератора без учета демпферных контуров. Такой процесс явля-
ется некоторым идеализированным КЗ, однако такое рассмотрение по-
зволяет выявить основные характерные черты процесса и является пер-
вой ступенью для изучения более сложных случаев.
Вывод уравнения переходного процесса при КЗ на выводах ге-
нератора.
При принятых допущениях (без учета влияния демпферных

86
контуров) переходный процесс определяется только контуром обмотки
возбуждения. Дифференциальное уравнение этого контура
f
f f f
d
i r U
dt
. (2.1.64)
Умножим (2.1.64) на М
ad
ω и разделим на r
f
f f
ad
f ad ad
f f
d U
M
i M M
r dt r
. (2.1.65)
Член в правой части уравнения (2.1.65) пропорционален напряжению
возбуждения и обозначается
Е
qe
f
qe ad
f
U
E M
r
.
Также заметим, что
f ad q
i M E
, поэтому
f
ad
q qe
f
d
M
E E
r dt
. (2.1.66)
В (2.1.66) первый член умножим и разделим на L
f
.
f ad f
q qe
f f
L M d
E E
L r dt
(2.1.67)
В (2.1.67) примем, что
0
f
d
f
L
T
r
,
где
0
d
T
– переходная постоянная времени по продольной оси при ра-
зомкнутой обмотке статора.
При неучете влияния демпферных контуров
0
d
T
равна постоянной
времени обмотки возбуждения. Также заметим, что согласно (
2.1.61)
f q
ad
f
d dE
M
L dt dt
,
поэтому уравнение (2.1.67) приводится к виду
0
.
q
d q qe
dE
T E E
dt
(2.1.66)
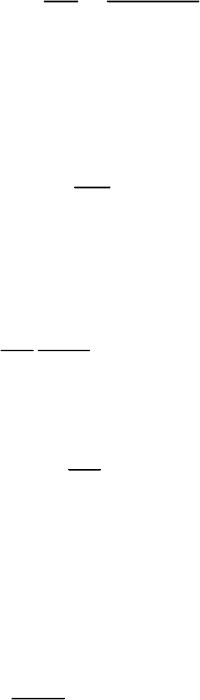
87
Для приведения уравнения (2.1.66) к одной переменной, например E
q
,
рассмотрим совместно выражения (2.1.56), (2.1.62) приведенные выше
,
.
q q d d
q q d d
U E I x
U E I x
(2.1.67)
В уравнениях (2.1.67) исключим ток I
d
и выразим
q
E
.
d d d
q q q
d d
x x x
E E U
x x
При трехфазном коротком замыкании на выводах генератора, работаю-
щего в режиме холостого хода, напряжение
0
q
U
, поэтому
.
d
q q
d
x
E E
x
(2.1.68)
Подставим (2.1.68) в (2.1.66)
0
.
q
d
d q qe
d
dE
x
T E E
x dt
Величина
0
d
d d
d
x
T T
x
есть постоянная времени по продольной оси при замкнутой накоротко
обмотке статора.
Далее решаем уравнение
.
q
d q qe
dE
T E E
dt
(2.1.69)
Решение уравнения (2.1.69) имеет вид
,
pt
q q
E E Ae
(2.1.70)
где Е
q∞
– установившееся значение Е
q
после переходного процесса.
В исходном установившемся режиме (в данном случае при холо-
стом ходе)
U
f
= U
f0
, i
f
= i
f0
и соответственно
0 0q f ad
E i M
,

88
0
0 0
f
qe ad f ad
f
U
E M i M
r
.
Важно обратить внимание на то, что в установившемся режиме в
уравнениях в форме ЭДС E
q
= E
q0
.
Примем, что регулирование возбуждения (форсировка возбужде-
ния) не производится, то есть
U
f
= U
f0
= const и, следовательно,
0
const
qe qe
E E
.
При таких условиях после окончания переходного процесса уста-
новившееся значение
Е
q
будет равно ее значению в предшествующем
установившемся режиме, то есть
0
q q
E E
.
Коэффициент А в (2.1.70) найдем из начальных условий при t = 0. В
соответствии с (
2.1.68) в момент короткого замыкания
(0) (0)
d
q q
d
x
E E
x
,
где
(0) (0)
,
q q
E E
– значения ЭДС непосредственно после кроткого замы-
кания.
ЭДС
q
E
пропорциональна потокосцеплению обмотки возбужде-
ния (2.1.61), то есть она не может измениться мгновенно и в первый
момент остается равной своему значению в предшествующем режиме
(0) 0
q q
E E
.
Так как в предшествующем режиме (ХХ) I
d
= 0, то
f f f
i L
и по
(2.1.61)
0 0 0
ad
q f f q
f
M
E i L E
L
. (2.1.71)
Таким образом, в момент короткого замыкания ЭДС Е
q
увеличива-
ется скачком и становится равной
(0) 0
.
d
q q
d
x
E E
x
Таким образом, из (2.1.70) при t = 0
(0) 0
(0) 0
,
.
q q
q q
E E A
A E E

89
Характеристическое уравнение по (2.1.69) и его корень
1
1 0, .
d
d
T p p
T
Окончательное решение уравнения (2.1.69)
0 (0) 0
( ) .
d
t
T
q q q q
E E E E e
Далее найдем закон изменения
q
E
используя соотношение (2.1.68)
0 (0) 0
( ) .
d
t
T
d d d
q q q q
d d d
x x x
E E E E e
x x x
(2.1.72)
По причинам, изложенным выше,
q
E
не изменяется в момент ко-
роткого замыкания и поэтому ее начальное значение остается равным
Е
q0
при холостом ходе в соответствии с (2.1.71). Поэтому (2.1.72) при-
мет вид
0
( ) ,
d
t
T
q q q q
E E E E e
где
0
d
q q
d
x
E E
x
.
Изменения ЭДС генератора при трехфазном КЗ показаны на рис.
2.1.19.
q
Е
q q
Е ,Е
q
Е
d
Т
d
2Т
d
3Т
d
4Т
t
q0
Е
q
Е
0
Рис. 2.1.19. Изменение ЭДС генератора при трехфазном КЗ

90
2.1.9. Система уравнений генератора в форме ЭДС
(с учетом влияния демпферных контуров
)
Из ранее полученных соотношений для вывода уравнений генера-
тора в форме ЭДС необходимы следующие
:
-
по оси «d» (2.1.19), (2.1.28), (2.1.29), (2.1.30),
-
по оси «q» (2.1.18), (2.1.31), (2.1.32).
Преобразования по оси «d». Из (2.1.30) и (2.1.29) выразим i
f
и i
D
.
Для определения i
D
умножим (2.1.30) на M
ad
, а (2.1.29) на L
f
2 2
f ad f ad f D ad d ad
M i M L i M I M
, (2.1.73)
2
D f D D f f ad f d ad f
L i L L i M L I M L
. (2.1.74)
Вычтем (2.1.74) из (2.1.73), сгруппируем члены, содержащие i
D
и I
d
, и
выразим искомый ток
i
D
2
2
D f f ad d ad f ad
D
D f ad
L M I M L M
i
L L M
. (2.1.75)
Для определения i
f
умножим (2.1.30) на L
D
, а (2.1.29) на M
ad
f D f D f D ad D d ad D
L i L L i M L I M L
. (2.1.76)
2 2
D ad D D ad f ad d ad
M i L M i M I M
. (2.1.77)
Вычтем (2.1.77) из (2.1.76), сгруппируем члены, содержащие i
D
и I
d
, и
выразим искомый ток
i
f
2
2
f D D ad d ad D ad
f
D f ad
L M I M L M
i
L L M
. (2.1.78)
Подставим (2.1.75) и (2.1.78) в (2.1.38), а затем в (2.1.19) и после преоб-
разований получим
2
2
2
2
.
f D ad ad D f ad
q
D f ad
ad f ad D ad
d d ad
D f ad
L M M L M
U
L L M
M L M L M
I L M
L L M
(2.1.79)
