Вайнштейн Р.А. Математические модели элементов электроэнергетических систем в расчетах установившихся режимов и переходных процессов
Подождите немного. Документ загружается.


61
во-вторых, при принятых (рис. 2.1.4) характеристиках состояние равно-
весия устойчиво. Это следует из простого качественного анализа:
- при отклонении от точки равновесия в сторону увеличения час-
тоты
0, 0
T Э
d
P P
dt
, то есть происходит торможение ротора аг-
регата и частота возвращается к прежнему значению;
- при отклонении частоты в сторону уменьшения
0, 0
T Э
d
P P
dt
и имеет место ускорение ротора и возврат к ис-
ходному режиму.
При рассмотрении установившихся режимов и переходных процес-
сов изменения частоты при общем синхронном движении генераторов
системы мощность турбин, как генерирующую часть обозначают
Р
Г
, а
электромагнитную мощность генератора, которая в таких режимах оп-
ределяется нагрузкой и потерями, обозначается
Р
Н
.
2.1.2. Вспомогательные понятия к математической модели
электромагнитного момента синхронной машины
Индуктивность.
При протекании тока i по обмотке создается на-
магничивающая сила (магнитодвижущая сила МДС
)
F = iw,
где w – число витков (рис. 2.1.5).
МДС создает магнитный поток, который определяется магнитным
сопротивлением
R
М
на его пути
U
i
w
l
S
Рис. 2.1.5. Магнитная цепь
M
iw
Ф
R
. (2.1.3)
В общем случае магнитное сопротивление равно

62
M
l
R
S
. (2.1.4)
где μ – магнитная проницаемость,
l – средняя длина магнитной линии,
S – площадь поперечного сечения магнитопровода.
Магнитная проницаемость
μ – это характеристика среды. Магнит-
ная проницаемость электротехнической стали много больше магнитной
проницаемости воздуха (и вообще неферромагнитных материалов).
Подставим (2.1.4) в (2.1.3
)
iwS
Ф
l
. (2.1.5)
Умножим левую и правую часть (2.1.5) на w
2
iw S
Фw
l
.
Учтем, что потокосцепление
Фw
. Тогда
2
w S
i
l
.
Как известно, коэффициент пропорциональности между потокос-
цеплением и током есть индуктивность цепи
Li
.
Таким образом,
2
w S
L
l
.
Собственная индуктивность, взаимная индуктивность, индук-
тивность рассеяния
. Рассмотрим два индуктивно-связанных контура
(рис. 2.1.6
), один из которых разомкнут. Магнитный поток, создаваемый
током
1
i
, в реальных электромагнитных системах состоит из двух со-
ставляющих:
- поток взаимной индукции, который полностью сцепляется с витками
первого и второго контуров,
- поток рассеивания, который сцепляется только с витками одного кон-
тура.
Дифференциальное уравнение для первого контура
1 12 1
12
1 1 1 1
( )
S S
d Ф Ф dФ
d
Ф
u w w w
dt dt dt
, (2.1.6)

63
где
1 1 1 12 1 12
,
S S
w
Ф wФ
.
1
s
Ф
12
Ф
1
u
2
u
1
i
Рис. 2.1.6. Индуктивно-связанные контуры
Сопоставим с потокосцеплениями соответственно индуктивность
рассеяния
L
S1
и взаимную индуктивность М
12
. Тогда
ψ
S1
= i
1
L
S1
, ψ
12
= i
1
М
12
.
Таким образом, уравнение (2.1.6) примет вид
1 1 1
1 1 12 1S
di di di
u L M L
dt dt dt
,
где
1 1 12
S
L L M
– собственная индуктивность.
Таким образом, полную (собственную) индуктивность контура
можно представить как сумму индуктивности рассеивания и взаимной
индуктивности.
1
u
1
S
L
2
S
L
12
M
2
u
1
i
2
i
Рис. 2.1.7. Схема замещения индуктивно-связанных контуров
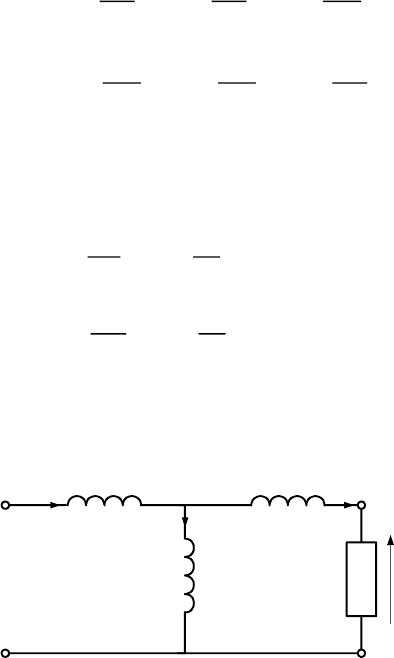
Если к зажимам второго контура подключить нагрузку (рис. 2.1.7),
то данной схеме будет соответствовать система уравнений
64
1 1 2
1 1 12 12
2 2 1
2 2 12 12
,
0.
S
S
di di di
u L M M
dt dt dt
di di di
u L M M
dt dt dt
После некоторых преобразований получим
1
1 1 12 1 2
2
2 2 12 1 2
( ),
( ) 0.
S
S
di
d
u L M i i
dt dt
di d
u L M i i
dt dt
(2.1.7)
Уравнениям (2.1.7) соответствует схема замещения рис.2.1.8.
1
u
1
S
L
2
S
L
12
M
2
u
1
i
2
i
1 2
i i
Рис. 2.1.8. Схема замещения, соответствующая уравнениям (2.1.7)
2.1.3. Индуктивные сопротивления синхронной машины
Индуктивные сопротивления синхронной машины, значения кото-
рых входят как коэффициенты в уравнения математической модели, оп-
ределяются при следующих условиях.
Сверхпереходное индуктивное сопротивление
(
d
x
) определяется в
первый момент внезапного (скачкообразного) изменения режима с уче-
том влияния демпферного контура и контура возбуждения.
Переходное сопротивление
(
d
x
) определяется расчетными усло-
виями, соответствующими первому моменту внезапного изменения ре-
жима без учета влияния демпферного контура.
Использование таких условий возможно в связи с тем, что свобод-
ные токи в демпферных контурах затухают значительно быстрее, чем в
обмотке возбуждения.

65
Для определения сопротивлений
d
x
и
d
x
;
q
x
используется теорема
о постоянстве потокосцепления с замкнутым контуром, активное сопро-
тивление которого равно нулю (сверхпроводящий контур).
Суммарное потокосцепление контура с собственной индуктивно-
стью
L, имеющего магнитную связь с другим контуром равно
K L M M
Li
,
где
M
– потокосцепление взаимоиндукции.
Дифференциальное уравнение такого контура
0
M
d L i
dt
.
Следовательно
const
M
L i
.
Последнее соотношение означает, что любое изменение потокос-
цепления взаимной индукции со сверхпроводящим контуром
M
вызы-
вает протекание тока в контуре такой величины и такого направления,
что поле этих токов компенсирует изменение
M
. Иными словами, ток
в сверхпроводящем короткозамкнутом контуре определяется из условия
сохранения потокосцепления с контуром неизменным.
Реальные контуры синхронной машины обладают, хотя и малыми,
но конечными активными сопротивлениями. Все же на некотором от-
резке времени, значительно меньшим постоянной времени контура,
можно последний рассматривать как сверхпроводящий и использовать
теорему о постоянстве потокосцепления.
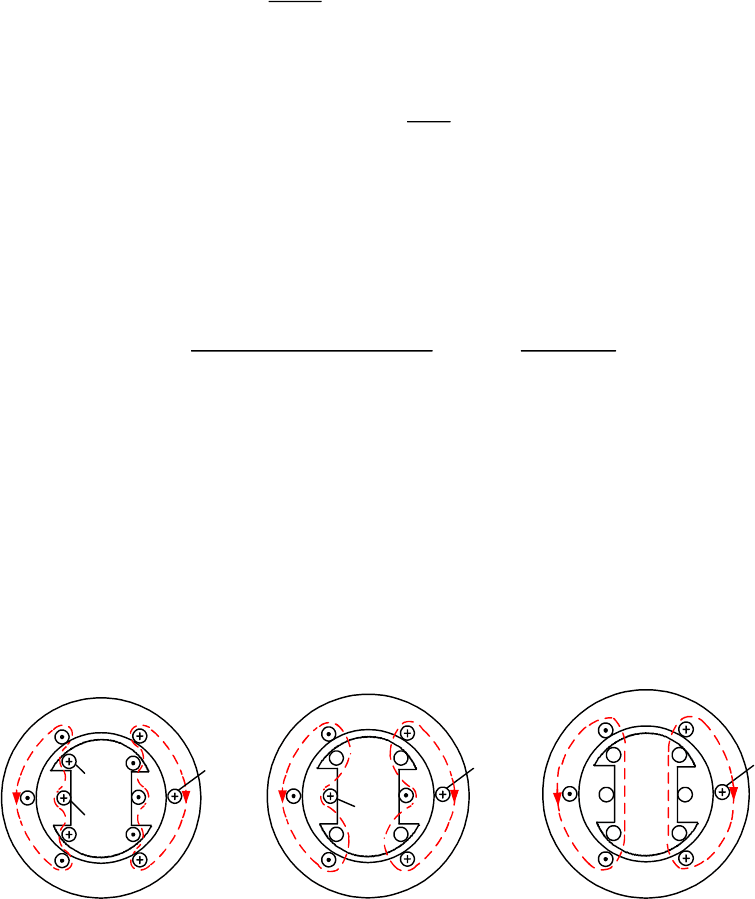
Применим теорему о постоянстве потокосцепления для магнитной
системы по рис.
2.1.9. Контур II является сверхпроводящим.
U
i
2
i
1
Ф
2
Ф
M
Ф
I
II
Рис.2.1.9. Магнитная система с двумя контурами
Уравнения для изменений потокосцеплений при изменении тока в
контуре
I
66
1 1 2 1
i L i M
, (2.1.8)
2 2 1 2
.
i L i M
(2.1.9)
Согласно теореме о постоянстве потокосцепления
2
0
. Выра-
зим при этих условиях
2
i
из уравнения (2.1.9), подставим в (2.1.8) и
выделим отношение
1
Э
L
i
, которое определяет результирующую
индуктивность контура
I
2
1
2
Э
M
L L
L
.
С учетом магнитного рассеивания контуров
1 1 2 2
,
L M L L M L
.
Тогда
2 1 1 2 2
1
2 2
Э
ML ML L L ML
L L
M L M L
.
Так как практически
2
M L
, то
1 2
Э
L L L
и это означает, что
все изменения тока
1
i
вызывают только изменения потока на пути рас-
сеивания. Магнитное сопротивление на пути рассеивания значительно
больше, поэтому индуктивность, а следовательно и индуктивное сопро-
тивление в первый момент изменения режима меньше.
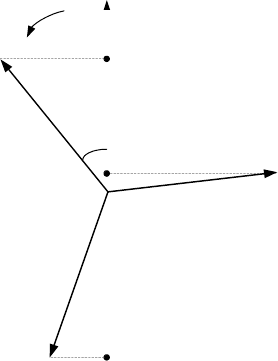
Подобная же картина имеет место в контурах синхронной машины,
что иллюстрируется на рис.2.1.10
.
А
В
С
D
i
f
i
А
I
Х
Y
Z
А
В
С
Y
Z
f
i
А
I
А
В
С
Х
Y
Z
А
I
а б в
Рис. 2.1.10. Магнитные поля периодических токов обмотки статора
а – в начальный момент внезапного КЗ, сверхпереходная стадия (
d
х
),
б – после затухания токов демпферной обмотки или при ее отсутствии (
d
х
),
в – при установившемся КЗ (
d
х
)
67
После затухания свободных токов в обмотке возбуждения и в
демпферных контурах магнитные потоки, создаваемые током обмотки
статора беспрепятственно замыкаются по наименьшему магнитному со-
противлению, которому соответствуют синхронные индуктивные со-
противления по продольной оси
– x
d
и по поперечной оси – x
q
. В син-
хронных машинах с явновыраженными полюсами на роторе магнитное
сопротивление по продольной оси значительно меньше, чем по попе-
речной и поэтому у таких машин
x
d
> x
q
.
2.1.4. Переход от трехфазной системы координат к прямоуголь-
ной системе
d-q координат, жестко связанной с ротором
(уравнения Парка
-Горева)
Переходный процесс в электрической машине любого типа может
быть описан системой дифференциальных уравнений в той или иной
системе координат. Выбор системы координат определяется конкрет-
ными условиями решаемой задачи.
При расчете переходного процесса может быть использована сис-
тема координат
d, q, 0, где оси d и q жестко связаны с ротором, причем
ось
d совмещена с продольной осью ротора и опережает ось q.
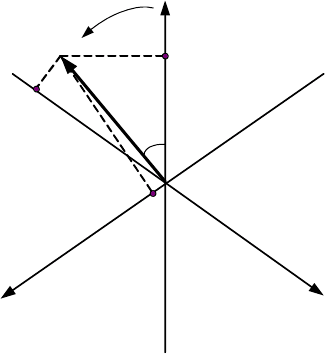
Мгновенные значения можно определить через векторы трехфазной
системы (рис. 2.1.11
).
Ось отсчета углов
A
F
B
F
С
F
А
f
В
f
С
f
Рис. 2.1.11. Определение мгновенных значений через векторы трехфазной системы
Из рис.2.1.11 очевидно
68
0
0
cos ,
cos( 120 ),
cos( 240 ).
A A
B B
C C
f F
f F
f F
Если принять для каждой фазы свои оси времени, сдвинутые отно-
сительно друг друга на 120
0
, то трехфазную симметричную систему
можно представить одним вектором
F, который называется обобщен-
ным вектором. Из рис. 2.1.12 очевидно, что проекция обобщенного век-
тора
F, вращающегося с угловой скоростью ω, на три оси времени даст
мгновенные значения трехфазных величин
0
0
cos ,
cos( 120 ),
cos( 240 ).
A
B
C
f F
f F
f F
c
b
fC
fB
fA
a
F
Рис. 2.1.12. Определение мгновенных значений через обобщенный вектор
Необходимо отметить, что чередование фаз для осей времени об-
ратно чередованию фаз, так как вращение осей времени противополож-
но вращению векторов.
Обобщенный вектор можно разложить на составляющие: продоль-
ную
F
d
, совпадающую с осью полюсов, и поперечную F
q.
(рис. 2.1.13).
Тогда мгновенные значения равны
0 0
0 0
cos sin ,
cos 120 sin 120 ,
cos 240 sin 240 .
a d q
b d q
c d q
f F F
f F F
f F F
(2.1.10)
где γ – угол между магнитной осью фазы А и осью d.
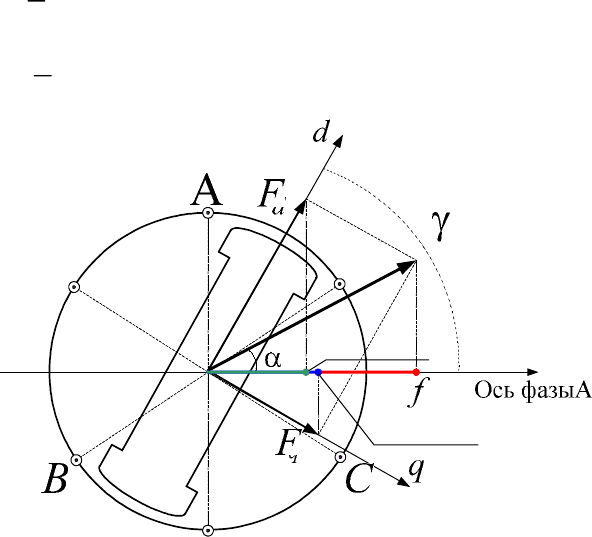
69
Из полученных уравнений можно выразить в явном виде F
d
и F
q
0 0
0 0
2
cos cos 120 cos 240 ,
3
2
sin sin 120 sin 240 .
3
d a b c
q a b c
F f f f
F f f f
(2.1.11)
cos( )
d
F
F
sin( )
q
F
Рис. 2.1.13. Обобщенный вектор F в системе координиат d-q
Для иллюстрации некоторых свойств преобразования координат
(2.1.11) рассмотрим два примера.
Пусть исходная трехфазная система токов симметрична и частота
их изменения равна частоте вращения ротора, то есть
cos
A m
i I t
,
0
cos 120
B m
i I t
,
0
cos 240
C m
i I t
.
Угол изменяется по закону γ = ωt+ γ
0
. При таких условиях по
(2.1.11) получаем
0
cos
d m
I I
,
0
sin
q m
I I
.
Как видно в данном случае составляющие I
d
и I
q
являются постоян-
ными во времени величинами. Токи
I
d
и I
q
создают соответствующие
намагничивающие силы (реакцию якоря), которые вместе с намагничи-
70
вающей силой, создаваемой током возбуждения, определяют результи-
рующий магнитный поток машины.
Угол (γ
0
– α) зависит от характера нагрузки генератора (рассматри-
вается далее с помощью векторных диаграмм).
Далее рассмотрим также симметричную трехфазную систему то-
ков, но будем считать, что частота их изменения не равна частоте вра-
щения ротора. Примем γ =
ω
1
t + γ
0
, причем ω
1
≠ ω.
В этом случае
1 0
cos
d m
I I t
,
1 0
sin
q m
I I t
.
Разность
1
S
есть частота скольжения. Таким образом, ре-
акция якоря по оси
d и q изменяется с частотой скольжения, во всех
замкнутых контурах по оси
d и по оси q наводятся токи с частотой
скольжения.
Напряжение на обмотке статора, например
, фазы А, равно
A
A A A
d
U r i
dt
,
где ψ
А
– полное потокосцепление обмотки фазы А,
i
A
, r
A
– соответственно ток фазы А и активное сопротивление обмотки.
Применим для тока и потокосцепления преобразование (2.1.10
)
cos sin
A d q
, (2.1.11)
cos sin
A d q
i I I
.
(2.1.12)
С учетом (2.1.11) и (2.1.12) получим
cos sin cos sin
A d q d A q A
d
U I r I r
dt
.
(2.1.13)
Преобразуем (2.1.13) с учетом того, что угол γ является функцией
времени
0
t
. (2.1.14)
cos sin sin
cos cos sin .
q
d
A d
q d A q A
d
d
d
U
dt dt dt
d
I r I r
dt
(2.1.15)
