Ваулина О.С., Щипицын А.Г. Комплекс для утилизации производственных отходов: математические модели и алгоритмы синтеза системы управления
Подождите немного. Документ загружается.


41
2.3.4. Линеаризация математической модели скруббера
Сначала проводится линеаризация системы. Для этого основные параметры
системы записываются в отклонениях:
);t(PP)t(P
скр
*
скрскр
δ+=
);t(PP)t(P
вод
*
водвод
δ+=
);t(PP)t(P
p
*
pp
δ+=
);t(МM)t(M
вых
*
выхвых
&&&
δ+=
);t(МM)t(M
вод
*
водвод
&&&
δ+=
).t(МM)t(M
р
*
рр
&&&
δ+=
Здесь: * – параметры на стационарном режиме (не зависят от времени).
Для магистрали преобразование уравнений проводится следующим образом.
(
)
()
;b)t(ММ
dt
)t(ММd
S
L
)t(PP)t(PP
вод
2
вод
*
вод
вод
*
вод
вод
вод
скp
*
скpвод
*
вод
&&
&&
δ++
+
δ+
=δ−−δ+
(
)
()
;
dt
)t(Мd
dt
)t(ММd
водвод
*
вод
&&&
δ
=
δ+
()
.0)t(М
2
вод
→δ
&
Так как
()
вод
2
*
вод
*
скp
*
вод
bМPP
&
=− – на стационарном режиме, то получаем:
()
(
)
()
;b)t(ММ2М
dt
)t(Мd
S
L
)t(P)t(PbМ
водвод
*
вод
2*
вод
вод
вод
вод
скpводвод
2
*
вод
&&&
&
&
δ++
+
δ
=δ−δ+
(
)
.b)t(ММ2
dt
)t(Мd
S
L
)t(P)t(P
водвод
*
вод
вод
вод
вод
скрвод
&&
&
δ+
δ
=δ−δ (2.3.11)
Преобразуем основные параметры в их безразмерные аналоги:
(
)
,
Ì
Ì
b)t(ÌÌ2
Ì
Ì
dt
)t(Ìd
S
L
P
P
)t(P
P
P
)t(P
*
âûõ
*
âûõ
âîäâîä
*
âîä
*
âûõ
*
âûõ
âîä
âîä
âîä
*
ñêp
*
ñêp
ñêp
*
ñêp
*
ñêð
âîä
&
&
&&
&
&
&
δ+
+
δ
=δ−δ
()
(
)
,Mb)t(MM2
M
dt
)t(Md
S
L
P)t(P)t(P
*
âûõâîäâîä
*
âîä
*
âûõ
âîä
âîä
âîä
*
ñêpñêpâîä
&&&
&
&
δ+
+
δ
=δ−δ

42
где
,
P
)t(P
)t(P
*
скp
вод
вод
δ
=δ
,
P
)t(P
)t(P
*
скp
скp
скp
δ
=δ
.
M
)t(M
)t(M
*
вых
вод
вод
&
&
δ
=δ
Преобразуем:
()
(
)
.M
P
b
)t(MM2
M
dt
)t(Md
PS
L
)t(P)t(P
*
вых
*
скp
вод
вод
*
вод
*
вых
вод
*
скpвод
вод
скpвод
&&&
&
&
δ+
+
δ
=δ−δ
(2.3.12)
Далее преобразуем по Лапласу:
()
.M
P
b
)s(MM2
M)s(M
PS
L
s)s(P)s(P
*
âûõ
*
ñêp
âîä
âîä
*
âîä
*
âûõâîä
*
ñêpâîä
âîä
ñêpâîä
&&&
&&
δ+
+δ=δ−δ
()
.M
P
b
M2M
PS
L
s)s(M)s(P)s(P
*
вых
*
скp
вод
*
вод
*
вых
*
скpвод
вод
водскpвод
+δ=δ−δ
&&&&
()
,1
bMS2
L
s)s(M
MbM2
P
)s(P)s(P
вод
*
водвод
вод
вод
*
выхвод
*
вод
*
скp
скpвод
+δ=δ−δ
&
&
&&
()
(
)
,1s)s(MС)s(P)s(P
водводводскpвод
+θδ=δ−δ
&
()
()
,0С)s(P)s(P)s(M1s
водскpводводвод
=δ−δ−δ+θ
&
(2.3.13)
где
,
MbM2
P
C
*
выхвод
*
вод
*
скp
вод
&&
=
.
bMS2
L
вод
*
водвод
вод
вод
&
=θ
Аналогичные преобразования произведем для выхода из реактора. В резуль-
тате чего получим систему уравнений:
()
()
()
=δ−δ−δ
=δ−δ−δ+θ
.0С)s(P)s(P)s(M
,0С)s(P)s(P)s(M1s
рскpрр
водскpводводвод
&
&
(2.3.14)
Для скруббера:

43
.
RT
)(q)t(P
SA)t(M)t(M
dt
)t(Pd
TR
скpскp
скp
выхскр3звод3зр
скp
скpскp
скp
λ
δ
−τ−δ+τ−δ=
δΩ
&&
(2.3.15)
.
RTM
P
)t(P
P)(q
SA
M
)t(M
M
)t(M
dt
P
)t(P
d
MTR
P
скpскp
*
вых
*
скp
скp
*
скp
выхскр
*
вых
3звод
*
вых
3зр
*
скp
скp
*
выхскpскp
*
скpскp
&
&
&
&
&
&
δ
λ
−
−
τ−δ
+
τ−δ
=
δ
Ω
;
RT
P)(q
SAMM
скpскp
*
скp
выхскр
*
вых
*
λ
==
&&
.
MTR
P
*
выхскpскp
*
скpскp
скp
&
Ω
=θ
).t(P
M
M
)t(M)t(M
dt
)t(Pd
скp
*
вых
*
вых
3звод3зр
скp
скp
δ−τ−δ+τ−δ=
δ
θ
&
&
&&
).t(P)t(M)t(M
dt
)t(Pd
скp3звод3зр
скp
скp
δ−τ−δ+τ−δ=
δ
θ
&&
(2.3.16)
Преобразуем (2.3.16) по Лапласу:
(
)
),s(Pe)s(M)s(M)s(Ps
скp
s
водрскpскp
3з
δ−δ+δ=δθ
τ−
&&
()
(
)
.e)s(M)s(M)s(P1s
3з
s
водрскpскp
τ−
δ+δ=δ+θ
&&
Окончательно для исследования устойчивости получаем систему уравнений:
()
()
()
()
()
=δ+δ−δ+θ
=δ−δ−δ
=δ−δ−δ+θ
τ−
.0e)s(M)s(M)s(P1s
,0Ñ)s(P)s(P)s(M
,0Ñ)s(P)s(P)s(M1s
3ç
s
âîäðñêpñêp
ðñêpðð
âîäñêpâîäâîäâîä
&&
&
&
(2.3.17)
Построим структурную схему для скруббера, используя систему уравнений
(2.3.17). Структурная схема представлена на рис. 2.6
.
δ
М
вод
.
-
τ
з3
s
e
С
вод
1 +
θ
вод
s
С
р
1
1 +
θ
скр
s
δ
P
р
δ
М
р
.
δ
М
вых
.
δ
P
скр
δ
P
вод
Рис. 2.6. Структурная схема системы (скруббер Вентури)

44
3. Параметрический синтез установки по критерию устойчивости
рабочих процессов
3.1. Анализ методов исследования устойчивости
Системы автоматического управления [51] могут содержать звенья, у которых
зависимость между входной U(t) и выходной y(t) величинами имеет вид:
),
t
(U)
t
(y τ−=
(3.1.1)
где τ
– постоянная величина, называемая временем запаздывания. Такие звенья
называют запаздывающими, так как они воспроизводят изменения входной вели-
чины без искажения, но с некоторым постоянным запаздыванием τ .
Передаточная функция запаздывающего звена:
.e)s(W
s
зап
τ−
=
(3.1.2)
Системы автоматического управления, содержащие хотя бы одно звено запаз-
дывания, называют системами с запаздыванием
. Процессы в системах с запазды-
ванием описываются дифференциально-разностными уравнениями.
Независимо от места включения запаздывающего звена характеристическое
уравнение системы с запаздыванием имеет вид:
.0e)s(R)s(Q)s(D
s
=+=
τ−
τ
(3.1.3)
Это характеристическое уравнение из-за наличия множителя
τ−s
e является не
полиномом, а трансцендентной функцией оператора s и в отличие от обыкновен-
ного алгебраического уравнения имеет бесконечное множество корней. Так как:
...,
!3
s
!2
s
s1e
3322
s
+
τ
−
τ
+τ−=
τ−
то (3.1.3) можно рассматривать как уравнение «бесконечной степени».
Необходимое и достаточное условие устойчивости: все корни уравнения
(3.1.3) должны быть левыми. Нахождение корней уравнения (3.1.3) затруднитель-
но, поэтому для исследования устойчивости систем с запаздыванием используют
критерии устойчивости.
Следует иметь в виду, что алгебраические критерии устойчивости Рауса и
Гурвица в их обычной форме для исследования систем с запаздыванием непри-
годны, причем для устойчивости линейных систем первого и второго порядков с
запаздыванием только положительности коэффициентов характеристического
уравнения уже становится недостаточно. Существуют различные алгебраические
критерии устойчивости для систем с запаздыванием, которые являются аналогами
критериев Рауса и Гурвица, однако в инженерной практике они широкого приме-
нения не нашли из-за их относительной сложности.
Для исследования устойчивости систем с запаздыванием можно применять ос-
нованные на принципе аргумента частотные критерии устойчивости Михайлова и
Найквиста либо метод D-разбиения.

45
Уравнение кривой (годографа) Михайлова системы с запаздыванием получают
после подстановки ω= js в характеристическое уравнение (3.1.3), т.е.
.0e)j(R)j(Q)e,j(D
jj
=ω+ω=ω
ωτ−ωτ−
τ
(3.1.4)
Наличие в (3.1.4) множителя
ωτ− j
e делает очертания кривой Михайлова доста-
точно сложным, и формулировка этого критерия для систем с запаздыванием ста-
новится не такой простой, как для обычных систем. Как показал Я.З. Цыпкин, для
исследования устойчивости систем с запаздыванием очень удобно применять
критерий устойчивости Найквиста.
Необходимым и достаточным условием асимптотической устойчивости ре-
шений стационарных линейных уравнений [60] является отрицательность дейст-
вительных частей всех корней характеристического квазиполинома.
Так как приближенное вычисление всех корней квазиполинома является зада-
чей весьма трудоемкой, то большое значение при исследовании на устойчивость
приобретают различные признаки отрицательности действительных частей всех
корней квазиполинома. Среди таких признаков чаще всего применяются следую-
щие:
1)
амплитудно-фазовый метод и его видоизменения;
2)
метод D-разбиений.
Ниже мы изложим основные идеи амплитудно-фазового метода, подробно раз-
работанного Я.З. Цыпкиным и метод D-разбиений.
3.1.1. Амплитудно-фазовый метод
Если функция f(z), аналитическая и отличная от нуля в точках некоторого про-
стого замкнутого контура С, внутри контура имеет лишь конечное множество
особых точек типа полюса [60], то
,PNds
)s(f
)s(f
i2
1
cc
С
'
−=
π
∫
(3.1.5)
где
c
N – сумма кратностей нулей функции f(s), расположенных внутри контура С,
а
c
P – сумма кратностей там же расположенных полюсов. Геометрическое истол-
кование этой теоремы о логарифмическом вычете приводит к «принципу аргу-
мента»:
.PN)s(Argf
2
1
ccc
−=∆
π
(3.1.6)
)s(Argf
c
∆ является полным приращением аргумента функции f(s) при одно-
кратном обходе точкой s в положительном направлении контура С. Другими сло-
вами, разность
cc
PN − равна числу полных оборотов, которые совершает в плос-
кости ω вектор, идущий из точки 0
=
ω
в точку )s(f
=
ω
. Когда точка s описывает
в положительном направлении контур С (число оборотов считается положитель-
ным, если вектор вращается против часовой стрелки, и считается отрицательным
при вращении по часовой стрелке).

46
Для получения условия отсутствия у характеристического квазиполинома )s(
ϕ
корней с положительными действительными частями применим принцип аргу-
мента к контуру
R
C
состоящему из отрезка мнимой оси [–iR, iR] и полуокружно-
сти радиуса R с центром в начале координат, лежащей в полуплоскости Re s > 0
(рис. 3.1), предварительно убедившись, что квазиполином не имеет нулей на мни-
мой оси.
Рис. 3.1. Условие отсутствия у характеристического квазиполинома )s(ϕ корней
с положительными действительными частями
Заметим, что в рассматриваемом случае Pc = 0. Воспользовавшись принципом
аргумента, находим из (3.1.6)
CR
N
и, если 0Nlim
CR
R
=
∞→
, то все корни s квазиполи-
нома удовлетворяют условию Re s < 0.
При применении этого общего метода к квазиполиному:
,e)s(Q)s(P)s(
s
1nn
τ−
−
+=ϕ
соответствующему уравнению n-го порядка (а также некоторым системам n-
уравнений первого порядка) с запаздыванием, где )s(P
n
и )s(Q
1n−
– полиномы со-
ответственно степени n и не выше n
–1, а можно несколько упростить исследова-
ние. Вместо функции )s(ϕ рассматривать функцию:
,e
)s(P
)s(Q
1
)s(P
)s(
s
n
1n
n
τ−
−
−=
ϕ
нули которой совпадают с нулями функции )s(
ϕ
(если )s(P
n
и )s(Q
1n−
не имеют
общих нулей) и имеющую полюсы в нулях многочлена
)s(P
n
.
Обозначим
.e
)s(P
)s(Q
)s(
s
n
1n
τ−
−
τ
−=ω Предельное положение при
∞
→R образа
контура
R
C при отображении )s(
τ
ω
называется амплитудно-фазовой характери-
стикой.
Так как
)s(1
)s(P
)s(
n
τ
ω−=
ϕ
, то нулями функции
)s(P
)s(
n
ϕ
соответствуют точки, в
которых
.1)s( =ω
τ
Поэтому, применяя принцип аргумента к функции
)s(
τ
ω
, надо
подсчитать число обходов амплитудно-фазовой характеристикой не точки s=0, а
точки s=1. Число обходов амплитудно-фазовой характеристикой точки s=1 равно
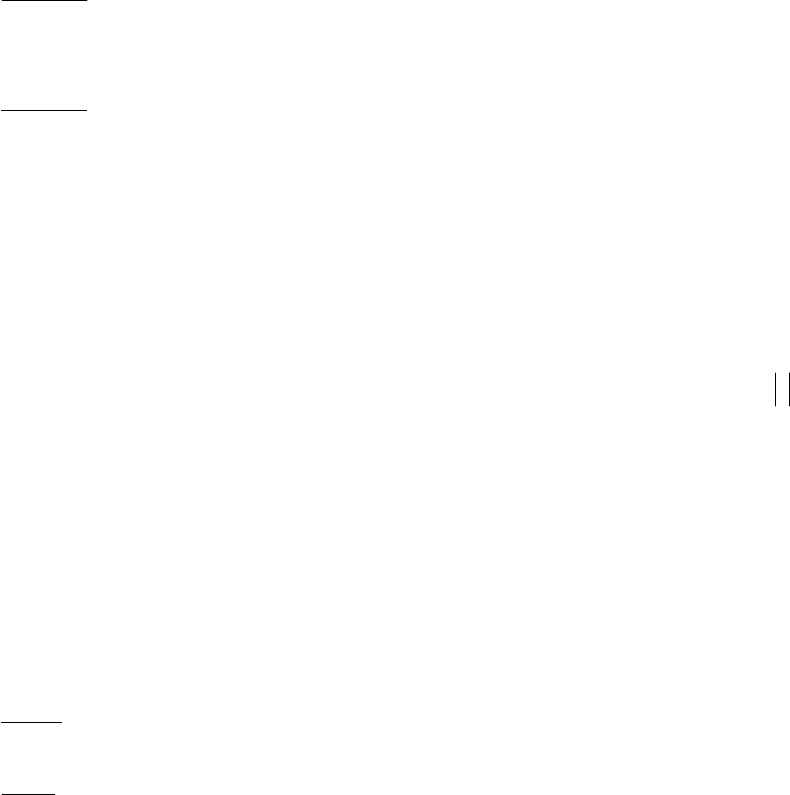
47
разности
cc
PN − и. Следовательно, для того чтобы 0N
c
=
, надо чтобы число об-
ходов амплитудно-фазовой характеристикой точки s=1 равнялось
c
P− . Еще раз
напомним, что при этом предполагается, что на мнимой оси нет нулей функции
)s(ϕ и что )s(P
n
и )s(Q
1n−
не имеют общих нулей, причем оба эти условия срав-
нительно легко проверяемы.
Заметим, что при отображении )s(
τ
ω
образ полуокружности, входящей в со-
став контура
R
C при ∞→R, стягивается в точку (так как степень )s(P
n
выше
степени
)s(Q
1n−
), и, следовательно, надо строить лишь образ мнимой оси, прохо-
димой в отрицательном направлении.
При построении амплитудно-фазовой характеристики удобно вначале найти
так называемую предельную характеристику, являющуюся предельным положе-
нием образа контура
R
C при отображении:
.
)s(P
)s(Q
)s(
n
1n
0
−
−=ω
Для построения образа мнимой оси при отображении:
τ−τ−
−
τ
ω=−=ω
s
0
s
n
1n
e)s(e
)s(P
)s(Q
)s(
или
τ−
τ
ω=ω
iy
0
e)iy()iy(,
зная уже предельную характеристику, достаточно учесть влияние множителя
τ−iy
e, поворачивающего, без изменения модуля, радиус-вектор точки предельной
характеристики, соответствующей значению y, на угол y
τ
−
.
При построении амплитудно-фазовой характеристики особое внимание сле-
дует уделить точкам предельной характеристики, лежащим на окружности
1s
=
,
так как именно эти точки при повороте на угол y
τ
−
могут попасть в точку s=1.
В качестве примера найдем область асимптотической устойчивости в про-
странстве коэффициентов a и b тривиального решения уравнения:
,0)t(b)t(ax)t(x =τ−++
&
(3.1.7)
где a, b и τ
– постоянные, 0>τ .
В рассматриваемом случае характеристическое уравнение имеет вид:
,0beas
s
=++
τ−
,
as
be
)s(
s
+
−=ω
τ−
τ
(3.1.8)
.
a
s
b
)s(
0
+
−=ω (3.1.9)
Предельной характеристикой является образ мнимой оси при дробно-
линейном отображении (3.1.9). При этом отображении мнимая ось переходит в
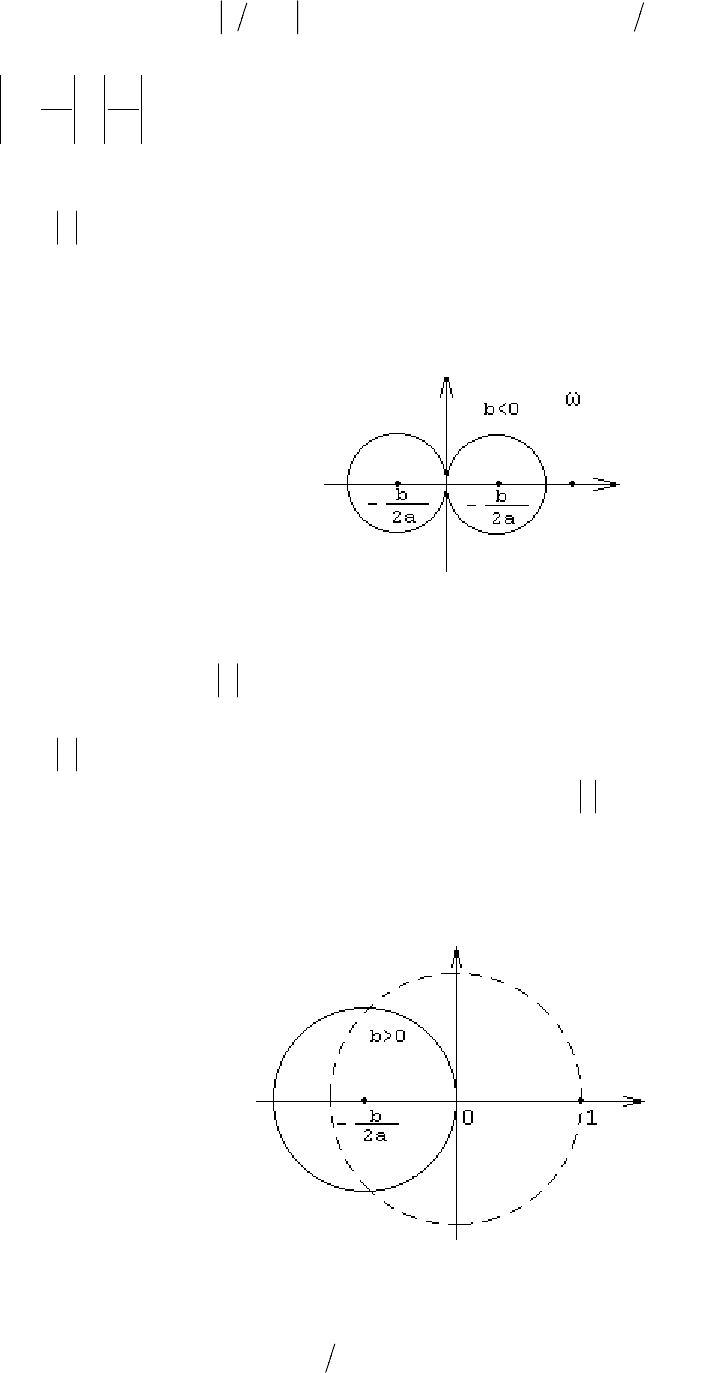
48
окружность радиуса )a2(b с центром в точке
)a2(bs
−
=
, уравнение которой
имеет вид:
.
a2
b
a2
b
s =+ (3.1.10)
Пусть 0
a
> , тогда функция )s(
τ
ω
не имеет полюсов в полуплоскости 0sRe >
и, если
ab < , то при любом повороте точек окружности (3.1.10) (рис. 3.2), вы-
званном наличием множителя
τ−iy
e в (3.1.8), амплитудно-фазовая характеристика
не будет охватывать точки s=1 и, следовательно, все нули квазиполинома
τ−
++
s
b
eas расположены в левой полуплоскости .0sRe <
Рис. 3.2. Образ мнимой оси при дробно-линейном отображении
Итак, при 0
a
> и ab < решения уравнения (3.1.7) асимптотически устойчивы
при любом 0≥τ .
При
0ab >> (рис. 3.3) для некоторых значений
τ
точки предельной характе-
ристики, лежащей одновременно и на окружности
1s
=
, изображенной на рисун-
ке пунктиром, могут перейти в точку s1=1. Наименьшее из этих значений
τ
при
заданных a и b будет значением, при переходе через которое решения уравнения
(3.1.7) теряют устойчивость, так как при переходе через это значение амплитудно-
фазовая характеристика начинает охватывать точку s=1.
Рис. 3.3. Амплитудно-фазовая характеристика и образ мнимой оси при дробно-линейном
отображении
Записав точку
(
)
aiyb)iy(
0
+
−=
ω
предельной характеристики в показатель-
ной форме, получим:
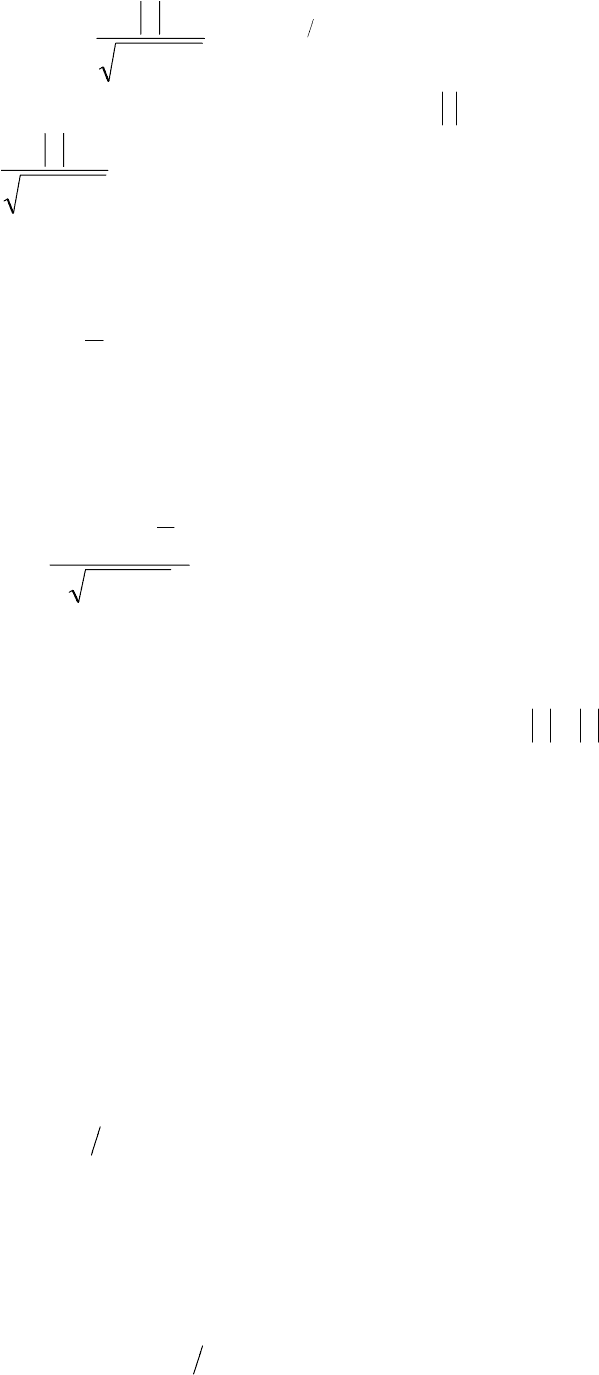
49
()
.e
ya
b
)iy(
ayarctgi
22
0
−⋅
⋅
+
=ω (3.1.11)
Если эта точка лежит на окружности
1s
=
, то:
,1
ya
b
22
=
+
(3.1.12)
а для того, чтобы после умножения на
τ−iy
e точка перешла в точку s=1, аргумент
τ−
ω
iy
0
e)iy( должен быть кратен
π
2:
.k2y
a
y
arctg π=τ−
− (3.1.13)
Наименьшее положительное значение
τ
, определяемое из (3.1.13), и является
тем критическим значением
τ
τ
=
0
, начиная с которого теряется устойчивость.
Используя (3.1.13) и (3.1.12) получаем:
.
ab
b
a
arccos
22
0
−
−
=τ
Если считать
τ
фиксированным, то, исключая из (3.1.12) и (3.1.13) параметр y,
получаем уравнение граничной кривой области устойчивости.
Аналогично проводится исследование и при 0
a
<
, надо лишь иметь в виду,
что при этом
1P
c
=
и поэтому, например, при ab
<
, когда амплитудно-фазовая
характеристика заведомо не может охватывать точки s=1, получаем неустойчи-
вость при любом
τ
, так как 0PN
cc
=
−
, откуда 1N
c
=
.
3.1.2. D-разбиение плоскости одного параметра [26]
Пусть требуется выяснить, в каких пределах можно изменять параметр
µ
, не
нарушая при этом устойчивости. Предположим, что
µ
входит в характеристиче-
ское уравнение замкнутой системы линейно и уравнение может быть приведено к
виду:
,02N1N =+⋅µ (3.1.14)
где N1 и N2 – полиномы от s.
Разрешим уравнение (3.1.14) относительно
µ
:
.1N2N−=µ (3.1.15)
Это равенство определяет зависимость параметра
µ
от значения корней харак-
теристического уравнения. Прежде всего, интересно выяснить, при каких значе-
ниях
µ система находится на границе устойчивости, т.е. какие значения
µ
соот-
ветствуют чисто мнимому корню
ω
j. Сделаем подстановку ω= js и построим на
комплексной плоскости (рис. 3.4) график функции:
,)(jY)(X)j(1N)j(2N)j(
ω
+
ω
=ω
ω
−=ωµ
(3.1.16)
при изменении
ω
от
∞−
до
∞
+ .

50
Функция )(X ω – четная функция
ω
, а )(Y
ω
– нечетная, поэтому искомая кри-
вая симметрична относительно вещественной оси и достаточно построить одну
ветвь кривой, изменяя
ω
от 0 до
∞
, а затем построить ее зеркальное отображение
относительно вещественной оси.
Рис. 3.4. Кривая D-разбиения в плоскости одного параметра
Полученную таким образом кривую называют кривой D-разбиения, она пред-
ставляет собой отображение мнимой оси плоскости корней характеристического
уравнения на плоскость параметра
µ
. Если, двигаясь по кривой от
−
∞→
ω
к
+∞→
ω
, наносить штриховку слева, то эта штриховка будет направлена в ту
часть плоскости параметра µ, которая соответствует левой полуплоскости кор-
ней.
Кривая D-разбиения разделяет плоскость параметра
µ
на несколько областей
(области 1, 2, 3 и 4 на рис. 3.4). Та из них, внутрь которой направлены штриховка
кривой, может быть областью устойчивости (область 4 на рис. 3.4). Теперь нужно
взять какую-либо точку
i
µ на оси абсцисс из этой области и, пользуясь любым
критерием устойчивости, построить устойчивость системы при
i
µ=µ . Если кри-
терий удовлетворяется, то рассматриваемая область есть область устойчивости.
Равенство (3.1.16) условно определяет параметр
µ
как комплексную величину,
На самом деле это вещественная величина и на плоскости
µ следует рассматри-
вать только точки, лежащие на вещественной оси. Поэтому значения параметра
µ, при которых система остается устойчивой, определяются отрезком положи-
тельной полуоси абсцисс, лежащим внутри области устойчивости.
3.2. Исследование устойчивости газогенератора
3.2.1. Построение областей устойчивости
Система уравнений для камеры сгорания и магистралей имеет вид:
()
()
=δ+δ−δ+θ
=δ−δ−δ+θ
=δ−δ−δ+θ
τ−
.0e))s(M)s(M()s(P)1s(
,0C))s(P)s(P()s(M1s
,0C))s(P)s(P()s(M1s
1з
s
огкскс
оксвхооо
гксвхггг
&&
&
&
(3.2.1)
