Ваулина О.С., Щипицын А.Г. Комплекс для утилизации производственных отходов: математические модели и алгоритмы синтеза системы управления
Подождите немного. Документ загружается.


31
+=−
+=−
+=−
.v
2
v
v
v
v
pv
в
2
в
в
в
в
pв
м
2
м
м
м
м
pм
b)t)(t(M
dt
)t(Md
S
L
)t(P)t(P
,b)t)(t(M
dt
)t(Md
S
L
)t(P)t(P
,b)t(M
dt
)t(Md
S
L
)t(P)t(P
&
&
&
&
&
&
(2.2.4)
2.2.2. Уравнение процессов, протекающих в реакторе
Время необходимое для дробления и смешения капель масла с воздухом и го-
рячими газами из газогенератора, смешения воды с горячим газом, нагрева ка-
пель, испарения, воспламенения и сгорания масла, характеризуется временем за-
паздывания
2з
τ
. Из-за наличия времени запаздывания будет изменяться и масса
поступающих в камеру компонентов.
Изменение массы в реакторе:
).t(M)t(M)t(M)t(M)t(M
dt
dM
р2зv2зм2зв2зкс
&&&&&
−τ−+τ−+τ−+τ−= (2.2.5)
Так как параметры процессов в реакторе считаем постоянными (кроме давле-
ния), то можно записать уравнение для массы продуктов сгорания в объеме каме-
ры (следует из уравнения состояния для абсолютного газа):
,
TR
)t(P
)t(M
pp
pp
Ω
=
где
р
Ω – объем реактора;
p
R – газовая постоянная продуктов сгорания в реакторе;
p
T – температура продуктов сгорания в реакторе.
Возьмем производную по времени данного уравнения:
.
dt
)t(dP
TRdt
)t(dM
p
pp
p
Ω
=
(2.2.6)
Массовый расход через сечение перед входом в скруббер Вентури [32]:
,
RT
)(q)t(P
SA)t(M
pp
p
скррр
λ
=
&
(2.2.7)
где
2
1
1k
1k
р
1k
2
kA
+
=
−
+
– коэффициент;

32
,
1k
1k
1
2
1k
)(q
1k
1
2
1k
1
−−
λ
+
−
−λ
+
=λ
где
k – показатель процесса;
скр
S – площадь сечения перед входом в скруббер.
Подставив в уравнение (2.2.5 ) значения
dt
)t(dM
и )t(M
р
&
, получаем:
.
RT
)(q)t(P
SA)t(M
)t(M)t(M)t(M
dt
)t(dP
TR
pp
p
kk2зv
2зм2зв2зкс
p
pp
p
λ
−τ−+
+τ−+τ−+τ−=
Ω
&
&&&
(2.2.8)
2.2.3. Уравнения движения для выхода из газогенератора
и входа в реактор
Запишем уравнение для главного входа в реактор (выход из газогенератора):
,const)t(M
êñ
=
&
(2.2.9)
так как происходит сверхзвуковое истечение продуктов сгорания из газогене-
ратора.
Обозначим:
.b)t(M
êñêñ
=
&
(2.2.10)
Таким образом, система уравнений (2.2.4), (2.2.8) и (2.2.10) описывает процес-
сы в технической системе, состоящей из реактора, трех трубопроводов и основно-
го входа в реактор из газогенератора:
λ
−τ−+τ−+
+τ−+τ−=
Ω
=
+=−
+=−
+=−
.
RT
)(q)t(P
SA)t(M)t(M
)t(M)t(M
dt
)t(dP
TR
,b)t(M
,b)t(M
dt
)t(Md
S
L
)t(P)t(P
,b)t(M
dt
)t(Md
S
L
)t(P)t(P
,b)t(M
dt
)t(Md
S
L
)t(P)t(P
pp
p
kk2çv2çì
2çâ2çêñ
p
pp
p
êñêñ
v
2
v
v
v
v
pv
â
2
â
â
â
â
pâ
ì
2
ì
ì
ì
ì
pì
&&
&&
&
&
&
&
&
&
&
(2.2.11)

33
Для моделирования переходных процессов полученную систему (2.2.11) необ-
ходимо преобразовать.
Преобразуем основные параметры в их безразмерные аналоги:
2*
ð
2*
ð
ì
2
ì
*
ð
*
ð
ì
ì
ì
*
ð
*
ð
ð
*
ð
*
ð
ì
Ì
Ì
b)t(M
Ì
Ì
dt
)t(Md
S
L
P
P
)t(P
P
P
)t(P
&
&
&
&
&
&
+=− ,
здесь: * – параметры на стационарном режиме (не зависят от времени).
Для магистралей воздуха и воды процедура нормирования основных парамет-
ров аналогична. Для процессов в реакторе:
.
P
P
RT
)(q)t(P
SA
Ì
Ì
)t(M
Ì
Ì
)t(M
Ì
Ì
)t(M
Ì
Ì
)t(M
dt
)t(dP
P
P
TR
*
ð
*
ð
pp
p
kk
*
ð
*
ð
2çv
*
ð
*
ð
2çì
*
ð
*
ð
2çâ
*
ð
*
ð
2çêñ
p
*
ð
*
ð
pp
p
λ
−τ−+τ−+
+τ−+τ−=
Ω
&
&
&
&
&
&
&
&
&
&
&
&
После некоторых преобразований получим систему уравнений для моделиро-
вания переходных процессов:
()
+++=+
=
−−=
−−=
−−=
τ−
,e)s(M)s(M)s(M)s(M)s(P1)sÀ(
,B)s(M
),s(MÂ))s(P)s(P(À)s(Ms
),s(MÂ))s(P)s(P(A)s(Ms
),s(MÂ))s(P)s(P(A)s(Ms
ç2s
êñvâìðð
êñêñ
2
vvpvvv
2
ââðâââ
2
ììðììì
&&&&
&
&&
&&
&&
(2.2.12)
где
,
P
Ì
L
S
À
*
p
*
p
i
i
i
&
= где i – магистрали масла, воздуха и воды,
,
ÌRÒ
Ð
À
*
ppp
*
pp
p
&
Ω
=
,
P
Ì
L
bS
Â
*
p
2*
p
i
ii
i
= где i – магистрали масла, воздуха и воды,
.
M
b
Â
*
p
êñ
êñ
&
=
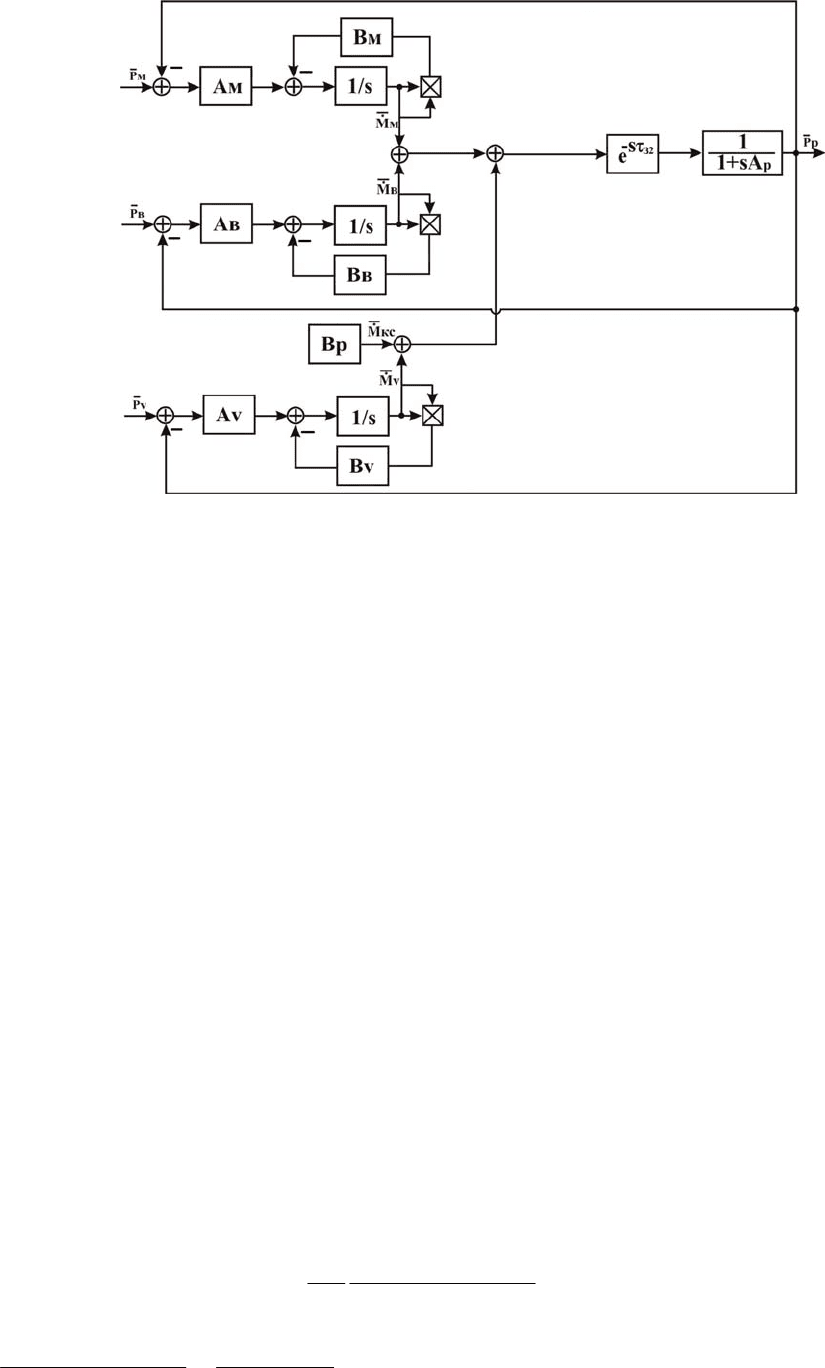
Построим структурную схему нелинейной системы, используя систему урав-
нений (2.2.12). Структурная схема представлена на рис. 2.3.
34
Рис. 2.3. Структурная схема нелинейной системы (реактор)
2.2.4. Линеаризация математической модели реактора
Сначала проводится линеаризация системы. Для этого основные параметры
системы записываются в отклонениях:
);t(PP)t(P
кс
*
кскс
δ+=
);t(PP)t(P
м
*
мм
δ+=
);t(PP)t(P
в
*
вв
δ+=
);t(PP)t(P
v
*
vv
δ+=
);t(PP)t(P
p
*
pp
δ+=
);t(MM)t(M
м
*
мм
&&&
δ+=
);t(MM)t(M
в
*
вв
&&&
δ+=
);t(MM)t(M
v
*
vv
&&&
δ+=
);t(MM)t(M
кс
*
кскс
&&&
δ+=
).t(MM)t(M
p
*
pp
&&&
δ+=
Здесь: * – параметры на стационарном режиме (не зависят от времени).
Для магистралей преобразование уравнений проводится следующим образом
(запишем только для магистрали масла, для воздуха и воды – аналогично).
(
)
()
;b)t(MM
dt
)t(MMd
S
L
)t(PP)t(PP
м
2
м
*
м
м
*
м
м
м
p
*
pм
*
м
&&
&&
δ++
δ+
=δ−−δ+
(
)
()
;
dt
)t(Md
dt
)t(MMd
мм
*
м
&&&
δ
=
δ+

35
()
.0)t(M
2
м
→δ
&
Так как
()
м
2
*
м
*
p
*
м
bMPP
&
=− – на стационарном режиме, то получаем:
()
(
)
()
;b)t(MM2M
dt
)t(Md
S
L
)t(P)t(PbM
мм
*
м
2*
м
м
м
м
pмм
2
*
м
&&&
&
&
δ++
δ
=δ−δ+
(
)
.b)t(MM2
dt
)t(Md
S
L
)t(P)t(P
мм
*
м
м
м
м
pм
&&
&
δ+
δ
=δ−δ (2.2.13)
Преобразуем основные параметры в их безразмерные аналоги:
(
)
,
M
M
b)t(MM2
M
M
dt
)t(Md
S
L
P
P
)t(P
P
P
)t(P
*
p
*
p
мм
*
м
*
p
*
p
м
м
м
*
p
*
p
p
*
p
*
p
м
&
&
&&
&
&
&
δ+
δ
=δ−δ
()
(
)
;Mb)t(MM2M
dt
)t(Md
S
L
P)t(P)t(P
*
pмм
*
м
*
p
м
м
м
*
ppм
&&&&
&
δ+
δ
=δ−δ
где
,
P
)t(P
)t(P
*
p
м
м
δ
=δ
,
P
)t(P
)t(P
*
p
p
p
δ
=δ .
M
)t(M
)t(M
*
p
м
м
&
&
δ
=δ
Преобразуем:
()
(
)
.M
P
b
)t(MM2M
dt
)t(Md
PS
L
)t(P)t(P
*
p
*
p
м
м
*
м
*
p
м
*
pм
м
pм
&&&&
&
δ+
δ
=δ−δ
(2.2.14)
Далее преобразуем по Лапласу:
()
.M
P
b
)s(MM2M)s(M
PS
L
s)s(P)s(P
*
p
*
p
м
м
*
м
*
pм
*
pм
м
pм
&&&&&
δ+δ=δ−δ
()
.M
P
b
M2M
PS
L
s)s(M)s(P)s(P
*
p
*
p
м
*
м
*
p
*
pм
м
мpм
+δ=δ−δ
&&&&
()
,1
bMS2
L
s)s(M
MbM2
P
)s(P)s(P
м
*
мм
м
м
*
pм
*
м
*
p
pм
+δ=δ−δ
&
&
&&
()
(
)
,1s)s(MС)s(P)s(P
мммpм
+θδ=δ−δ
&
()
()
,0С)s(P)s(P)s(M1s
мpммм
=δ−δ−δ+θ
&
(2.2.15)
где
,
MbM2
P
C
*
pм
*
м
*
p
м
&&
=
.
bMS2
L
м
*
мм
м
м
&
=θ
Аналогичные преобразования произведем для магистралей воздуха и воды и
для выхода из газогенератора. В результате чего получим систему уравнений:
36
()
()
()
()
()
()
=δ
=δ−δ−δ+θ
=δ−δ−δ+θ
=δ−δ−δ+θ
.C)s(M
,0Ñ)s(P)s(P)s(M1s
,0Ñ)s(P)s(P)s(M1s
,0Ñ)s(P)s(P)s(M1s
êñêñ
vpvvv
âpâââ
ìpììì
&
&
&
&
(2.2.16)
Для реактора:
.
RT
)(q)t(P
SA)t(M
)t(M)t(M)t(M
dt
)t(Pd
TR
pp
p
kk2зv
2зв2зм2зкс
p
pp
p
λδ
−τ−δ+
+τ−δ+τ−δ+τ−δ=
δΩ
&
&&&
(2.2.17)
+
τ−δ
+
τ−δ
+
τ−δ
=
δ
Ω
*
p
2çâ
*
p
2çì
*
p
2çêñ
*
p
p
*
ppp
*
pp
M
)t(M
M
)t(M
M
)t(M
dt
P
)t(P
d
MTR
P
&
&
&
&
&
&
&
.
RTM
P
)t(P
P)(q
SA
M
)t(M
pp
*
p
*
p
p
*
p
kk
*
p
2çv
&&
&
δ
λ
−
τ−δ
+
;
RT
P)(q
SAMM
pp
*
p
kk
*
р
*
λ
==
&&
.
MTR
P
*
ppp
*
pp
p
&
Ω
=θ
).t(P
M
M
)t(M)t(M)t(M)t(M
dt
)t(Pd
p
*
*
2зv2зв2зм2зкс
p
p
δ−
−τ−δ+τ−δ+τ−δ+τ−δ=
δ
θ
&
&
&&&&
).t(P)t(M
)t(M)t(M)t(M
dt
)t(Pd
p2зv
2зв2зм2зкс
p
p
δ−τ−δ+
+τ−δ+τ−δ+τ−δ=
δ
θ
&
&&&
(2.2.18)
Преобразуем (2.2.18) по Лапласу:
(
)
),s(Pe)s(M)s(M)s(M)s(M)s(Ps
p
s
vвмксpp
2з
δ−δ+δ+δ+δ=δθ
τ−
&&&&
()
(
)
.e)s(M)s(M)s(M)s(M)s(P1s
2з
s
vвмксpp
τ−
δ+δ+δ+δ=δ+θ
&&&&
(2.2.19)
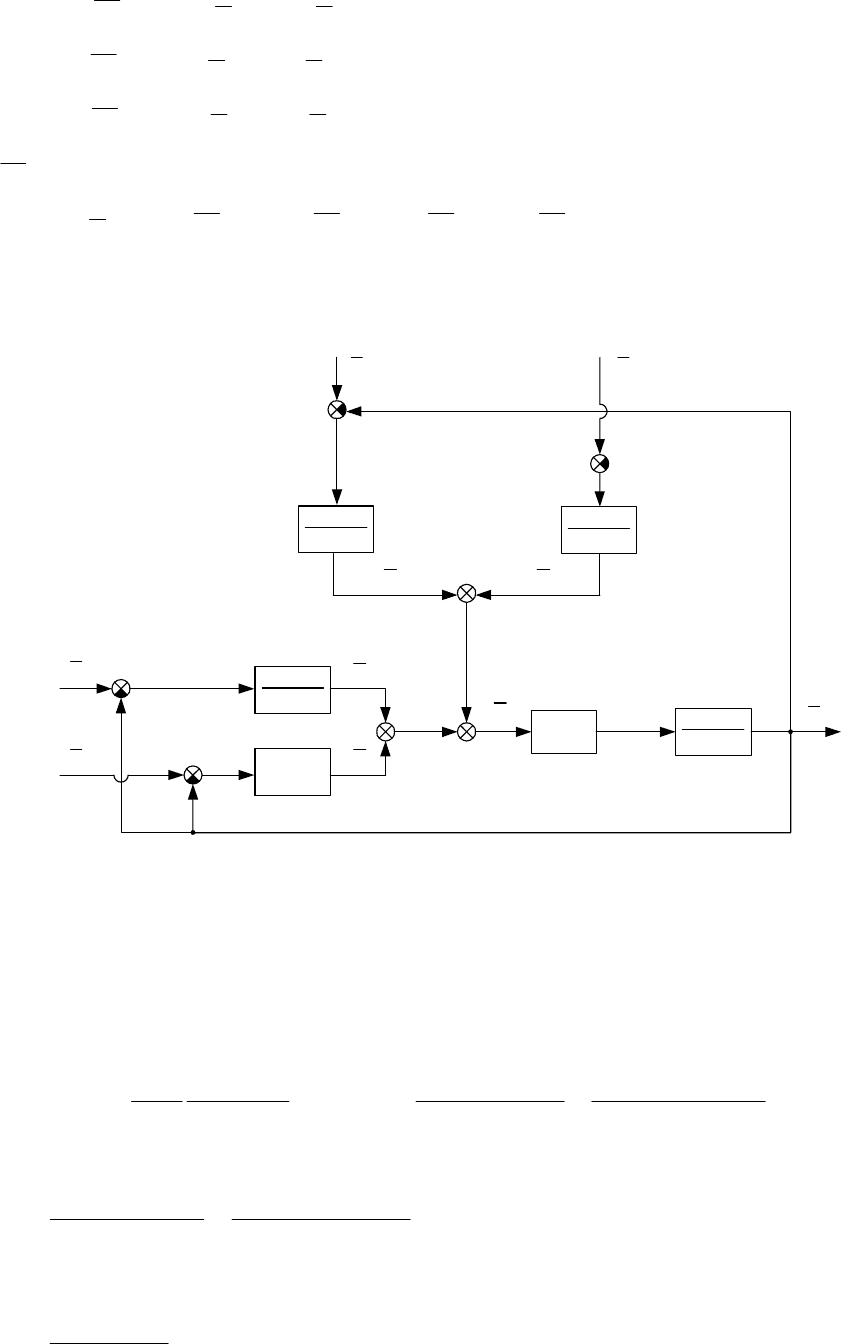
Окончательно для исследования устойчивости получаем систему уравнений:
37
()
()
()
()
()
()
()
()
=δ+δ+δ+δ−δ+θ
=δ
=δ−δ−δ+θ
=δ−δ−δ+θ
=δ−δ−δ+θ
τ−
.0e)s(M)s(M)s(M)s(M)s(P1s
,C)s(M
,0Ñ)s(P)s(P)s(M1s
,0Ñ)s(P)s(P)s(M1s
,0Ñ)s(P)s(P)s(M1s
2ç
s
vâìêñpp
êñêñ
vpvvv
âpâââ
ìpììì
&&&&
&
&
&
&
(2.2.20)
Построим структурную схему для реактора, используя систему уравнений
(2.2.20). Структурная схема представлена на рис. 2.4.
δ
P
м
δ
М
м
.
-
τ
з2
s
e
С
в
1 +
θ
в
s
С
v
1 +
θ
v
s
С
м
1 +
θ
м
s
С
кс
1
1 +
θ
p
s
δ
P
кс
δ
P
в
δ
P
v
δ
М
кс
.
δ
М
p
.
δ
М
в
.
δ
М
v
.
δ
P
p
Рис. 2.4. Структурная схема системы (реактор)
2.3. Математическая модель скруббера Вентури
2.3.1. Уравнения движения в магистрали воды
Уравнение для магистрали воды:
,
S2
2
Sd2
L
)t(M
dt
)t(Md
S
L
)t(P)t(P
2
водвод
2вод1вод
2
водводвод
водтрвод
2
вод
вод
вод
вод
скрвод
ρ
ξ+ξ+
+
ρ
ξ
+=−
&
&
(2.3.1)
обозначим:
.
S2
2
Sd2
L
b
2
водвод
2вод1вод
2
водводвод
водтрвод
вод
ρ
ξ
+
ξ+
+
ρ
ξ
=
На стационарном режиме:
.
M
PP
b
2*
вод
*
скр
*
вод
вод
&
−
=
Получим уравнение, описывающее процессы в магистрали воды:

38
.b)t(M
dt
)t(Md
S
L
)t(P)t(P
вод
2
вод
вод
вод
вод
скрвод
&
&
+=− (2.3.2)
2.3.2. Уравнение процессов протекающих в скруббере
Время необходимое для торможения потока на форсунках, ускорения в су-
жающейся части скруббера, равномерного движения в горле (цилиндрической
части), и замедления потока в расширяющейся части, характеризуется временем
запаздывания
3з
τ
. Из-за наличия времени запаздывания будет изменяться и масса
поступающих в камеру компонентов.
Изменение массы в скруббере:
).t(M)t(M)t(M
dt
dM
вых3звод3зp
&&&
−τ−+τ−= (2.3.3)
Так как параметры процессов в скруббере считаем постоянными (кроме дав-
ления), то можно записать уравнение для массы продуктов сгорания в объеме
скруббера (следует из уравнения состояния для абсолютного газа):
,
TR
)t(P
)t(M
скpскp
скрскр
Ω
=
где
скр
Ω – объем скруббера;
скp
R – газовая постоянная продуктов сгорания в скруббере;
скp
T – температура продуктов сгорания в скруббере.
Возьмем производную по времени данного уравнения:
.
dt
)t(dP
TRdt
)t(dM
скp
скpскp
сp
Ω
= (2.3.4)
Массовый расход на выходе из скруббера Вентури [32]:
,
RT
)(q)t(P
SA)t(M
скpскp
скp
выхскрвых
λ
=
&
(2.3.5)
где
2
1
1k
1k
скр
1k
2
kA
+
=
−
+
– коэффициент;
,
1k
1k
1
2
1k
)(q
1k
1
2
1k
1
−−
λ
+
−
−λ
+
=λ
k – показатель процесса;
вых
S – площадь сечения на выходе скруббера.
Подставив в уравнение (2.3.3 ) значения
dt
)t(dM
и )t(M
вых
&
, получаем:

39
.
RT
)(q)t(P
SA
)t(M)t(M
dt
)t(dP
TR
ñêpñêp
ñêð
âûõñêð
3çâîä3çð
ñêp
ñêpñêp
ñêp
λ
−
−τ−+τ−=
Ω
&&
(2.3.6)
2.3.3. Уравнения движения для выхода из реактора и входа
в скруббер Вентури
Запишем уравнение для главного входа в скруббер (выход из реактора):
,
S2
2
)t(M)t(P)t(P
2
рр
р
2
рскрр
ρ
ξ+
=−
&
(2.3.7)
обозначим:
.
S2
2
b
2
рр
р
р
ρ
ξ+
=
На стационарном режиме:
.
M
PP
b
2*
р
*
скp
*
р
р
&
−
=
Получим уравнение, описывающее процессы на выходе из реактора и входе в
скруббер:
.b)t(M)t(P)t(P
р
2
рскрр
&
=− (2.3.8)
Таким образом, система уравнений (2.3.2), (2.3.6) и (2.3.8) описывает процессы
в технической системе, состоящей из скруббера, трубопровода воды и основного
входа в скруббер из реактора:
λ
−τ−+τ−=
Ω
=−
+=−
.
RT
)(q)t(P
SA)t(M)t(M
dt
)t(dP
TR
,b)t(M)t(P)t(P
,b)t(M
dt
)t(Md
S
L
)t(P)t(P
ñêpñêp
ñêð
âûõñêð3çâîä3çð
ñêp
ñêpñêp
ñêp
ð
2
ðñêðð
âîä
2
âîä
âîä
âîä
âîä
ñêðâîä
&&
&
&
&
(2.3.9)
Для моделирования переходных процессов полученную систему (2.3.9) необ-
ходимо преобразовать. Основные параметры преобразуем в их безразмерные ана-
логи:
2*
âûõ
2*
âûõ
âîä
2
âîä
*
âûõ
*
âûõ
âîä
âîä
âîä
*
ñêð
*
ñêð
ñêð
*
ñêð
*
ñêð
âîä
Ì
Ì
b)t(M
Ì
Ì
dt
)t(Md
S
L
P
P
)t(P
P
P
)t(P
&
&
&
&
&
&
+=− ,
здесь: * – параметры на стационарном режиме (не зависят от времени).
40
,
P
Ì
b)t(M
dt
)t(Md
P
Ì
S
L
))t(P)t(P(
*
ñêð
2*
âûõ
âîä
2
âîä
âîä
*
ñêð
*
âûõ
âîä
âîä
ñêðâîä
&
&
&
&
+=−
;
P
)t(P
)t(P
*
ñêð
âîä
âîä
= .
M
)t(M
)t(M
*
âûõ
âîä
âîä
&
&
&
=
Для выхода из реактора процедура нормирования основных параметров анало-
гична. Для процессов в скруббере Вентури:
,
P
P
RT
)t(P
SA
Ì
Ì
)t(M
Ì
Ì
)t(M
P
P
dt
)t(dP
RÒ
*
ñêð
*
ñêð
ñêðñêð
ñêð
âûõñêð
*
âûõ
*
âûõ
3çð
*
âûõ
*
âûõ
3çâîä
*
ñêð
*
ñêðñêð
ñêðñêð
ñêð
−τ−+
+τ−=
Ω
&
&
&
&
&
&
После преобразований получим систему уравнений для моделирования пере-
ходных процессов:
()
+=+
=−
−−=
τ−
,e)s(M)s(M)s(P1)sÀ(
),s(M))s(P)s(P(Â
),s(MÂ))s(P)s(P(A)s(Ms
ç3s
ðâîäñêðñêð
2
ðñêððñêð
2
âîäâîäñêðâîäâîäâîä
&&
&
&&
(2.3.10)
где
,
P
Ì
L
S
À
*
ñêð
*
âûõ
âîä
âîä
âîä
&
=
,
ÌRÒ
Ð
À
*
âûõñêðñêð
*
ñêðñêð
ñêð
&
Ω
=
,
P
Ì
L
bS
Â
*
ñêð
2*
âûõ
âîä
âîäâîä
âîä
&
=
.
Ìb
Ð
Â
2*
âûõð
*
ñêð
ñêð
=
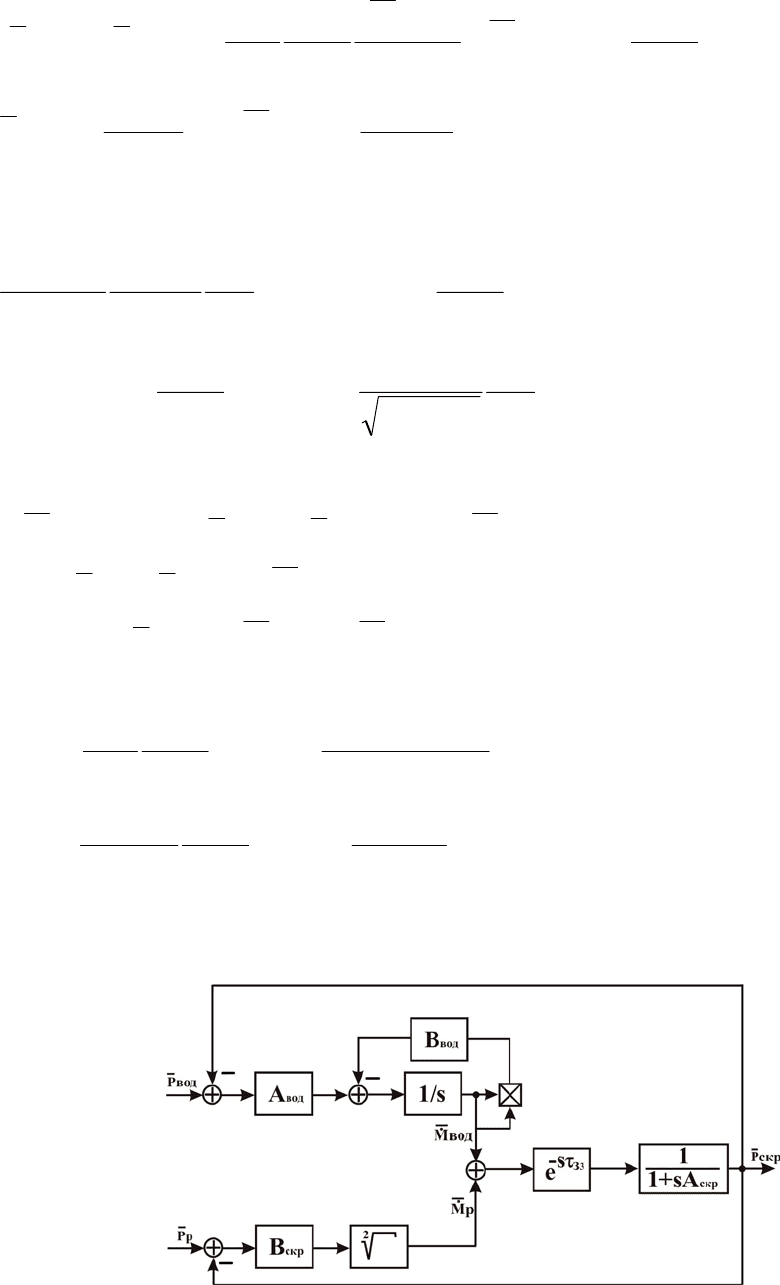
Построим структурную схему нелинейной системы, используя систему урав-
нений (2.3.10). Структурная схема представлена на рис. 2.5.
Рис. 2.5. Структурная схема нелинейной системы (скруббер Вентури)
