Вафин Д.Б. Задания по физике
Подождите немного. Документ загружается.


Поглощательная способность пластинки:
а = I
погл
/I
o
= (I
1
– I
2
)/I
o
= (1 r)(1 e
–
l
).
Из закона сохранения энергии
а +
+
= 1
Поэтому полная отражательная способность пластинки
= 1 – а –
= r [1+ (1 r) e
–
l
].
При получении этих формул пренебрегли вторичными отражениями.
Отношение пропускательных способностей двух пластинок
2
1
2
1
l-
l-
e
e
τ
τ
= e
(l 2 – l 1)
.
Отсюда линейный коэффициент поглощения вещества
=
12
2
1
)/ln(
ll
ττ
.
Анализ размерности:
[
] = 1/[l] = 1/м.
Решение:
=
12
2
1
)τ/(τ
ll
ln
=
3
10)49
)748,0/852,0(
(
ln
= 26 м
-1
.
r =
2
21
21
1
1
n
n
=
2
411
4,11
,
= 0,0278.
а
1
= (1 r)(1 e
–
l1
) = (1 – 0,0278)(1 – e
–260,004
) = 0,096.
а
2
= (1 r)(1 e
–
l2
) = (1 – 0,0278)(1 – e
–260,009
) = 0,203.
1
= r [1+ (1 r) e
–
l1
] = 0,028[1 + (1 – 0,028) e
–260,004
] = 0,052.
2
= r [1+ (1 r) e
–
l2
] = 0,028[1+(1 – 0,028) e
–260,009
] = 0,049.
Ответ:
Линейный коэффициент поглощения вещества пластинок
= 26 м
–1
.
Поглощательные способности пластинок соответственно:
а
1
= 0,096 и а
2
= 0,203.
Полные отражательные способности соответственно:
1
= 0,052 и
2
= 0,049.
Можно обратить внимание на то, что у поглощающих пластинок
полные отражательные способности зависят от толщины пластинок, в
130
то время как для не поглощающих пластинок полная отражательная
способность от толщины не зависит и определяется выражением
= 1 (1 r)
2
.
8.1..2. Атомная физика
Атом состоит из положительно заряженного ядра, вокруг кото-
рого движутся электроны. Количество электронов атома равняется
порядковому номеру Z элемента в периодической системе Менделее-
ва. Ядро состоит из положительно заряженных протонов и электриче-
ски нейтральных нейтронов. Количество протонов ядра также равня-
ется порядковому номеру элемента: N
e
= N
p
= Z. Протоны и нейтроны
еще называют нуклонами. Заряды протона и электрона равны по абсо-
лютной величине и равны элементарному заряду: q
p
= +e; q
e
= –e
.
Так как электроны имеют волновые свойства, одновременно оп-
ределить их координаты и импульс не удается. Можно лишь устано-
вить геометрическое место точек, с наибольшей вероятностью обна-
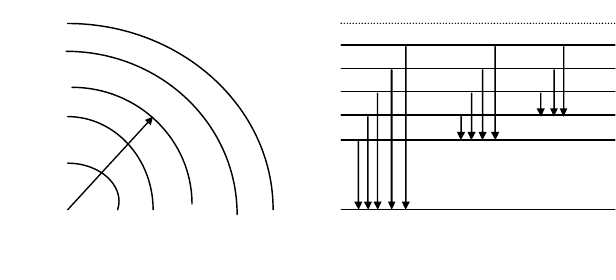
ружения электронов. Эти места условно можно назвать орбитами
электронов (рис. 48).
Самая близкая к ядру орбита обозначается номером n = 1. Орби-
ты электронов (электронные слои обозначают, также заглавными бук-
вами латинского алфавита : K, L, M, N, O, и т.д. У электрона, оторвав-
шегося из атома, n = . Каждой орбите соответствует энергетический
уровень атома. При переходе из высокого уровня на более низкий уро-
131
n = 5 n =
n = 4 n = 6
n = 5
n = 3 n = 4
n = 2 n = 3
n = 2
n = 1 r
3
Серия Серия
Бальмера Пашена
n = 1
K L M N O Серия Леймана
Рис. 48. Орбиты электронов и электронные уровни атомов.

вень излучается квант энергии E
n
k
= h
.
Частота излучения водородоподобных ионов при переходе с n –
й орбиты на k – ю орбиту
v
n
k
= RZ
2
(
22
11
nk
),
где z – порядковый номер элемента; R – постоянная Ридберга, равная
R =
32
4
ε8 h
me
o
= 3,2910
15
, с
–1
,
где m, e – масса и заряд электрона, соответственно.
Иногда за постоянную Ридберга принимают величину
R
= R/c.
Согласно первому постулату Бора движение электронов вокруг
ядра возможно только по стационарным орбитам, радиусы которых
удовлетворяют условию квантования орбитального момента импуль-
са электрона
mr
n
= n
π
h
2
,
где n – номер стационарной орбиты (главное квантовое число); r
n
–
радиус стационарной орбиты;
– скорость электрона на этой орбите,
m – масса электрона.
Радиус n - й боровской орбиты определяется выражением
r
n
= n
2
2
2
me
z
hε
о
.
Согласно второму постулату Бора, частота излучения при перехо-
де с n – й орбиты на k – ю орбиту
v
n
k
=
h
W
W
kn
,
где W
n
, W
k
– энергия электрона на этих орбитах (n k).
Энергия электрона находящегося на n -ой орбите, равна
W
n
=
22
4
2
2
ε8 h
me
n
o
z
.
Частота v
o
, соответствующая коротковолновой границе сплошно-
го рентгеновского спектра, может быть определена из соотношения
hv
o
= eU,
где U – разность потенциалов между электродами рентгеновской
трубки.
132

При переходах электронов внутренних оболочек многоэлектрон-
ных атомов излучаются фотоны высокой частоты – характеристи-
ческое рентгеновское излучение. Длина волны характеристического
рентгеновского излучения может быть вычислена по формуле Мозли
v = R(Z – )
2
(
22
11
nk
),
где Z – порядковый номер элемента, из которого сделан анод,
по-
стоянная экранирования.
Для рентгеновских К – спектров:
= 1; k = 1, n =2, 3, …;
для L
спектров:
= 7, 5; k = 2, n = 3, 4, …;
Уменьшение интенсивности I параллельного пучка рентгенов-
ских лучей при прохождении ими в веществе пути l подчиняется за-
кону Бугера – Ламберта
I = I
o
e
–
l
,
где
линейный коэффициент поглощения. Массовый коэффициент
поглощения
m
связан с линейным коэффициентом поглощения со-
отношением:
m
=
/
, где
плотность вещества.
Дифракция рентгеновских лучей на кристаллах описывается урав-
нением Вульфа – Брэгга:
2d sin
= k, (k = 0, 1, 2, ….),
где d – постоянная решетки кристалла (расстояние между атомными
плоскостями),
угол скольжения (угол между пучком рентгенов-
ских лучей и поверхностью кристалла).
Соотношения неопределенностей Гейзенберга:
xp
x
ħ, yp
y
ħ, zp
z
ħ,
где ħ =
π
h
2
, p
x
, p
y
, p
z
– интервалы, в которых заключены проек-
ции импульса частицы по осям x, y, z.
Соотношение неопределенности для энергии
W t
ħ,
где W – разность двух значений энергии микрообъекта, разделенных
интервалом времени t.
Вероятность нахождения частицы в объеме dV:
dW =
=
2
dV,
133

где = (x, y, z, t) – волновая функция, описывающая состояние час-
тицы;
функция, комплексно сопряженная с ,
2
– квадрат
модуля волновой функции определяет плотность вероятности нахож-
дения частицы в данной точке пространства.
Уравнение Шредингера для стационарных состояний
+ 2m/ ħ
2
(E – U) = 0,
где = (x, y, z) – пространственная часть волновой функции ( =
(x, y, z, t) = (x, y, z)exp(–iEt/ħ); U =U(x, y, z) – потенциальная энер-
гия частицы; Е полная энергия частицы.
Волновая функция, описывающая одномерное движение сво-
бодной частицы
(x, t) = А ехр(– i(Et – p
x
)/ ħ),
где А – амплитуда волн де Бройля, р
х
= kħ – импульс частицы, Е = ħ
энергия частицы.
Собственные значения энергии частицы, находящейся на n-м
энергетическом уровне в одномерной прямоугольной «потенциальной
яме» с бесконечно высокими «стенками»
E
n
= n
2
2
ħ
2
/(2ml
2
) , n = 1, 2, 3, …,
где l – ширина ямы.
Собственная волновая функция, соответствующая вышеприве-
денному собственному значению энергии
n
(x) = )/2( l sin(n
x/l) , n = 1, 2, 3, …
Принцип Паули: в любой квантовой системе не может быть двух
электронов с одинаковым набором всех четырех квантовых чисел n, l,
m
l
, m
s
.
Здесь n = 1, 2, 3, …. – главное квантовое число; l - 0, 1, …, n – 1
– орбитальное квантовое число; m
l
= –l,…, 0, …, +l – магнитное кван-
товое число; m
s
= 1/2 – спиновое квантовое число.
Совокупность электронов с одинаковыми значениями n и l обра-
зует электронную оболочку. Совокупность оболочек с одинаковыми
значениями n образуют группу или электронный слой.
Слои электронов обозначают буквами:
n 1 2 3 4 5 6 7
Слой K L M N O P Q
134

Состояния электронов в оболочке обозначают буквами:
l 0 1 2 3 4 5
Состояние s p d f g h
Максимальное число электронов в слое:
N
макс
=
1
)12(2
- n
0 l
l = 2n
2
.
Момент импульса (механический орбитальный момент импульса)
электрона:
L
l
= ħ )( 1ll ,
где l орбитальное квантовое число.
Проекция момента импульса на направление Z внешнего магнит-
ного поля:
L
iz
= ħm
l
,
где m
l
магнитное квантовое число.
Правило отбора для орбитального и магнитного квантовых чи-
сел:
l = 1 и m
l
= 0, 1.
Спин (собственный механический импульса) электрона:
L
s
= ħ )( 1ss ,
где s – спиновое квантовое число (s = ½).
Проекция спина на направление z внешнего магнитного поля:
L
sz
= ħm
s
,
где m
s
магнитное квантовое число (m
s
= ½).
Пример решения и оформления задач
Сколько различных состояний может иметь электрон с главным
квантовым числом n =3?
Анализ и решение:
При n = 3 орбитальное квантовое число l может принимать зна-
чения: 0, 1, 2. При l = 2 магнитное квантовое число m
l
может прини-
135

мать значения: –2, –1, 0, 1, 2, что дает пять различных состояний. В
каждом из этих состояний спиновое квантовое число m
s
может быть
либо +1/2, либо –1/2. Поэтому при l = 2 электрон может находиться в
25 = 10 различных состояниях. При l =1 магнитное квантовое число
m
l
может принимать значения:–1, 0, 1; а так как спин m
s
может быть
либо +1/2, либо –1/2, получаем еще 6 различных разрешенных состоя-
ний. Наконец, при l = 0, магнитное квантовое число m
l
может быть
m
l
= 0. Поэтому существует только 2 разрешенных состояния для
двух значений m
s
. Таким образом, общее число состояний равно
10 + 6 + 2 = 18.
Ответ:
С главным квантовым числом n =3 электрон может иметь 18 различ-
ных разрешенных состояний.
8.1.3. Ядерная физика
Некоторые тяжелые элементы испуская
–,
–,
– лучи пре-
вращаются в ядра других элементов. Этот процесс называется есте-
ственной радиоактивностью. При радиоактивном распаде со време-
нем количество радиоактивных элементов уменьшается. Временное
уравнение радиоактивного распада
N = N
o
e
–
t
,
где N
о
– первоначальное число радиоактивных атомов, N – число ато-
мов, не распавшихся к моменту времени t,
постоянная радиоак-
тивного распада.
Связь между постоянной распада , средним временем жизни
, и
периодом полураспада Т
= 1/
= (ln2)/T.
Число распадов, происходящих в препарате за единицу времени,
называется активностью радиоактивного распада:
а =
dt
dN
= –
N, (1Бк = 1 расп./с) – беккерель.
Если радиоактивный препарат А с постоянной распада
А
поме-
щен в закрытый сосуд и при распаде образуется также радиоактивный
препарат В с постоянной распада
В
, то число атомов вещества В к
моменту времени t
136
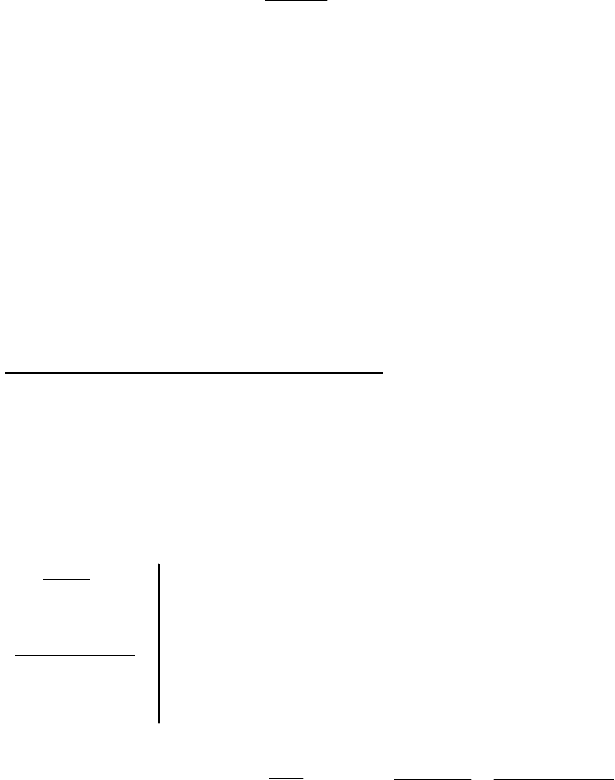
N
B
= N
A
)(
λλ
λ
tt
eе
BА
АВ
А
,
где N
A
– количество атомов препарата А в начальный момент времени.
Энергия, необходимая для расщепления ядра на составляющие
его нуклоны называется энергией связи ядра:
W = c
2
m
я
,
где с – скорость света в вакууме, m
я
– дефект массы ядра.
m
я
= z m
p
+ (A – z)m
n
– m
я
,
где z – порядковый номер изотопа, А – массовое число, m
p
масса
протона, m
n
– масса нейтрона, m
я
– масса ядра изотопа.
В последней формуле вместо массы ядра m
я
можно взять массу
соответствующего изотопа, в этом случае вместо массы протона m
p
следует взять массу изотопа
1
1
H .
Пример решения и оформления задач
В лаборатории имеется 1,49 мкг чистого
13
7
N с периодом полу-
распада 10,0 мин. 1) Сколько ядер
13
7
N содержалось первоначально в
образце? 2) Чему равна начальная активность? 3) Чему равна актив-
ность через 1 час? 4)Через какое время активность упадет менее чем
до одного распада в секунду?
Анализ и решение:
1) Общее число ядер образца в данный момент
N
o
= N
A
m/
,
где N
A
= 6,0210
23
– число Авогадро,
= 13 г –
атомная масса изотопа. Таким образом
N
o
= N
A
m/
= 6,0210
23
1,4910
-9
/1310
-3
= 6,910
16
ядер.
2) Начальная активность
а
o
=
dt
dN
= N
о
=
6010
109,6693,0
693,0
16
T
N
o
=
=8,010
13
расп./с.
В формуле для активности не учитывали знак минус, показы-
вающий знак скорости распада.
137
Дано
:
m = 1,49 мкг
t
1
= 1 час
Т = 10,0 мин
1) N
o
; 2) а
о
;
3) а
1
; 4) t

3) Активность в момент времени t
1
а =
N = N
o
e
t
= а
o
e
t
= 8,010
13
e
–(0,00163600)
= 1,2310
12
с
–1
.
4) Определим момент времени t, по истечении которого
а =
N
o
e
t
= 1. Отсюда e
t
= 1/
N
o
. Поэтому
t =
0016,0
)109,60016,0(
)
16
λ
λ
ln
Nln
o
(
= 2,7610
4
с.
Ответ:
1) Начальное количество ядер в образце – N
o
=6,910
16
ядер.
2) Начальная активность препарата а
o
= 8,010
13
расп./с.
3) Активность препарата через 1 час а =1,2310
12
расп./с.
4) Через t = 2,7610
4
с или t = 7,66 час активность упадет менее чем
до одного распада в секунду.
8.2. Задания по ядерной физике (Задание 12)
Поставить недостающие обозначения в сокращенной форме запи-
си ядерной реакции. Вычислить энергию ядерной реакции. Какая
суммарная энергия ядерной реакции, если в реакции участвует 0,5 мо-
лей исходного вещества?
1) Be
9
(d, x)Li
7
. 2) N
15
(x, p)O
18
. 3) H
2
(d, p)X.
4) H
2
(x, )n. 5) Li
6
(d, )X. 6) X(p, )He
3
.
7) Be
9
(d, x)B
10
. 8) X(d, n)Be
8
. 9) H
2
(x, p)He
4
.
10) X(, p)O
17
. 11) Al
27
(x, p)Si
30
. 12) Al
27
(n, x)Na
24
.
13) Li
7
(p, n)X. 14) X(, p)O
17
. 15) Li
7
(x, n)Be
7
.
16) Li
7
( , x)B
10
. 17) Be
9
( n, )X. 18) X( d, )N
14
.
19) B
10
( x, )Li
7
. 20) Be
9
( , x)C
12
. 21) Na
24
( p, x)Ne
20.
22) X( p, n)Ar
37
. 23) O
17
( d, n)X. 24) B
10
( x, )Be
8
.
25) C
13
( x, n)N
14
. 26) X( n, )Be
9
. 27) Be
9
( x, )Li
7
.
28) N
14
( n, x)C
14
. 29)X( p, )Na
22
. 30) N
15
( p, x)C
12
.
138

Библиографический список
1. Детлаф А.А., Яворский Б.М. Курс физики: Учебное пособ. для
втузов. М.:Высш. шк., 2001. 718 с.
2. Трофимова Т.И. Курс физики.: Учебное пособие для вузов.
М.:Высш. шк., 1990. 478 с.
3. Кухлинг Х. Справочник по физике: Пер. с нем. М.:Мир, 1982.
520 с.
П Р И Л О Ж Е Н И Е
Некоторые основные физические постоянные
Скорость света в вакууме с = 2,99792510
8
м/с
Ускорение свободного падения g = 9,81 м/с
2
Гравитационная постоянная
= 6,67210
-11
м
3
/(кгс
2
)
Универсальная газовая постоянная R = 8,31441 Дж/(мольК)
Нормальный молярный объем V
= 22,41383 м
3
/кмоль
Постоянная Авогадро N
А
= 6, 02204510
23
моль
-1
Число Лошмидта N
L
= 2,68675410
25
м
-3
Постоянная Больцмана k = 1,38066210
–23
Дж/К
Постоянная Планка h = 6,6261710
–34
Джс
= h/2 = 1,054610
–34
Джс
Постоянная Стефана – Больцмана
= 5,668710
–8
Втм
–2
К
-4
Постоянная Вина (смещения) b
1
= 2,897810
–3
мК
Электрическая постоянная
о
= 8,85418710
–12
Ф/м
Магнитная постоянная
о
= 1,25663710
–6
Гн/м
Число Фарадея F
= 9,64845610
4
Кл/моль
Масса покоя электрона m
e
= 9,109510
–31
кг
Масса покоя протона m
р
= 1,6726485 10
–27
кг =
= 1,00727647 а.е.м.
Масса покоя нейтрона m
n
= 1,6749543 10
–27
кг =
= 1,0086650 а.е.м.
Элементарный заряд е = 1,602189210
–19
Кл
Удельный заряд электрона е/m
e
= 1,758804710
11
Кл/кг
Атомная единица массы а.е.м. = 1,660565510
–27
кг =
= 931501,59 кэВ
Радиус Бора r
1
= 5,2917710
–11
м
Постоянная Ридберга R = 3,2910
15
с
–1
R
= R/c = 1,097410
7
м
–1
139
