Вафин Д.Б. Задания по физике

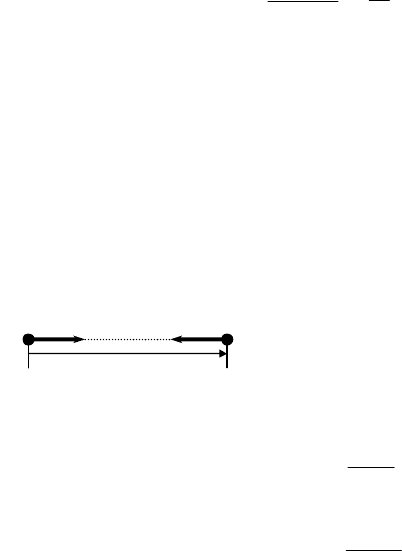
Центром инерции системы материальных точек называют такую

точку С, радиусвектор которой определяется по формуле:

r

c

=







n

i

n

i

ii

m

1

r

=





n

i

ii

m

1

r ,

где m

i

, r

i

– масса и радиус-вектор i-й точки системы, m – общая масса

всей системы.

Если тело можно было бы шарнирно закрепить в центре инерции,

то оно оставалось бы в состоянии равновесия при любом повороте.

Импульс системы равен произведению массы всей системы на

скорость ее центра инерции:

р =





n

i

1

р = mv

c

.

Изучая движение небесных тел и па-

дение тел в земных условиях, Ньютон ус-

тановил, что две материальные точки

притягиваются друг к другу с силой F,

пропорциональной их массам m

1

, m

2

и об-

ратно пропорциональной квадрату рас-

стояния r между ними:

F =



2

21

r

m

.

Закон Всемирного тяготения в векторной форме:

F

21

= –



3

21

r

mm

r

21

.

Здесь F

21

– сила, действующая на m

2

со стороны m

1

(Рис. 4); r

21

– ради-

ус–вектор m

2

относительно m

1

; r = r

21

 ;



= 6,6710

–11

Нм

2

/кг

2

– грави-

тационная постоянная. Знак « – » показывает, что F

21

и r

21

имеют про-

тивоположные направления.

Сила тяжести: F

т

= mg, где g – ускорение свободного падения.

Пусть под действием внешней силы F упругое тело деформиру-

ется (рис. 5); l

o

– начальный размер, l



конечный размер; x = l – l

o

–

величина деформации.

10

m

1

F

12

F

21

m

2

r

21

Рис. 4

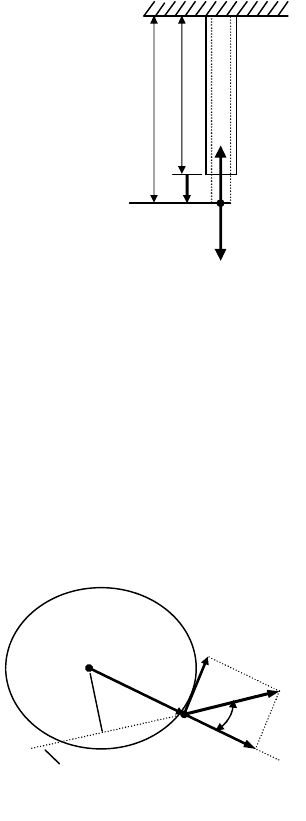
За счет смещения узлов кристаллической

решетки возникает сила упругости F, препятст-

вующая внешней силе F

.

Если после прекращения внешнего воздей-

ствия тело восстанавливает первоначальные раз-

меры и форму, то деформация называется абсо-

лютно упругой.

При абсолютно упругой деформации сила

упругости F, возникающая при малых деформа-

циях, пропорциональна деформации тела х:

F =  k x , (закон Гука)

где k – коэффициент упругости.

Знак минус показывает, что сила упругости

направлена в сторону, противоположную на-

правлению деформации.

Иногда закон Гука представляют в относительной форме:









,

где  = F/S – нормальное напряжение; S – площадь поперечного сече-

ния тела;



= х /l

o

– относительная деформация; Е – модуль упругости,

характеризующая упругие свойства тела (вещества).

Коэффициент упругости кроме свойств тела зависит и от его гео-

метрических параметров. Например, для стержня:

k = ES/l

o

.

Момент инерции системы N материальных точек определяет

инертность тела при вращательном движении:

J = m

r

i

N

i





1

2

,

где r

i

– расстояние от i



й материаль-

ной точки массой m

i

до оси враще-

ния О.

Момент инерции цилиндра

J = m R

2

/2.

Вращающий момент силы относи-

тельно оси О (рис. 6)

M = r F



 r sin



F = h F,

где h = r sin



 плечо силы F, кратчайшее расстояние от оси вра-

щения до линии действия силы F (ось перпендикулярна чертежу).

11

l l

o

F

x

F 

Рис. 5

F



O  ось

r F

h

А



F

r

Линия действия силы

Рис. 6

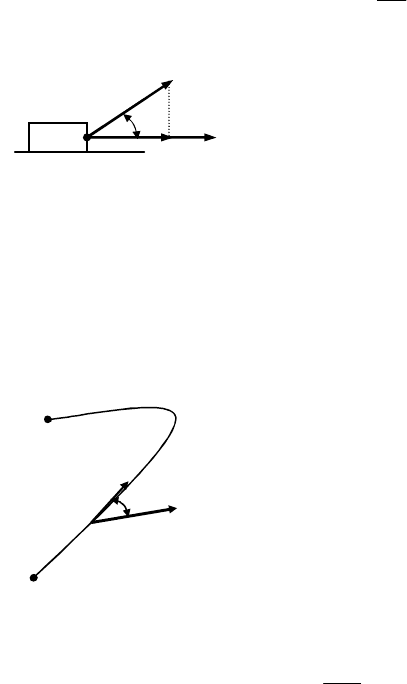
Закон динамики вращательного движения

M = J β



=

dt

dL

,

где L = J

ω



 момент импульса тела, вектор, направленный вдоль

ω



.

Пусть под действием силы F тело m

массой совершает перемещение l (рис. 7).

Очевидно, что перемещение тела обуслов-

лено только касательной (тангенциальной) к

траектории составляющей силы F



:

F



= F cos



.

Работой силы называется физическая величина, равная произве-

дению тангенциальной составляющей силы F



на перемещение l:

A = F



l = F cos



 l = Fl, Дж,

где F



 проекция силы F на направление перемещения l,



 угол

между направлениями силы и перемещения.

Работа постоянного вращающего момента

А = М .

Работа переменной силы, совершаемая при

перемещении тела из точки 1 в точку 2 (Рис. 8) ,

равна сумме элементарных работ на отдельных

бесконечно малых участках пути. Эта сумма

приводит к интегралу:

А =







N

1i

iii

N

lαF Δcos

lim

=



2

1

dl αF cos

.

Мгновенной мощностью силы F называется

физическая величина, численно равная работе,

совершаемой этой силой за единицу времени:

N =

d

dt

A

, Вт.

Энергия является физической величиной, служащей единой мерой

различных форм движения материи.

Энергия механической системы характеризует эту систему с точ-

ки зрения возможных в ней количественных и качественных превра-

щений движения. Эти превращения обусловлены взаимодействием тел

системы как между собой, так и внешними телами.

12

F

m



l

F



Рис. 7

2

l

i

 F

i

1

Рис.

8

Механическая энергия складывается из кинетической и потенци-

альной энергии:

W = W

к

+ W

п.

Кинетическая энергия это энергия движущегося тела, равняется

работе, которую может совершить тело при его торможении до пол-

ной остановки.

Кинетическая энергия поступательно движущегося тела опреде-

ляется по формуле:

W

к

=

2

m



.

Если работа силы затрачивается только на изменение кинетиче-

ской энергии тела, то имеет место соотношение:



2

1

dlFcos



= W

К2

– W

К1.

Кинетическая энергия тела, вращающегося относительно непод-

вижной оси:

2

вр

к



J

W 

,

где J – момент инерции тела,



 угловая скорость.

Если тело в каждой точке пространства подвержено воздействию

других тел, то говорят, что это тело находится в силовом поле.

Силу F, действующую на материальную точку называют консер-

вативной или потенциальной, если работа А

1–2

, совершаемая этой си-

лой при перемещении материальной точки из одного положения 1 в

другое положение 2, не зависит от того, по какой траектории это пе-

ремещение произошло(рис. 9):

А

1–а–2

= А

1–b–2

= А

1–2

.

Все силы, не удовлетворяющие этому условию,

называются неконсервативными, или диссипатив-

ными.

Если на систему тел действуют консервативные

силы, то можно ввести понятие потенциальной энер-

гии этой системы. Работа перемещения А

1–2

в поле

консервативных сил полностью определяется на-

чальной и конечной состояниями системы. Поэтому

ее можно выразить как разность значений некоторой

функции состояния системы W

п

(x,y,z), зависящей

13

1

F



a F

b

2

Рис. 9

только от координат всех материальных точек системы:

А

1–2

= W

П1

– W

П2

.

Эту функцию называют потенциальной энергией системы.

Из данного соотношения следует, что работа консервативных сил,

действующих на механическую систему, равна убыли потенциальной

энергии этой системы при переходе из состояния 1 в состояние 2.

Для определенности, в каком-то состоянии потенциальную энер-

гию системы считают равной нулю. Пусть потенциальная энергия пе-

ремещаемого тела равна нулю для состояния 2: W

П2

= 0. Тогда потен-

циальная энергия этого тела в произвольном состоянии 1:

W

П1

= A

1–2

.

Потенциальная энергия тела обусловлена взаимодействием этого

тела с другими телами системы (нахождением тела в поле консерва-

тивных сил) и численно равняется работе, которую совершают силы

поля, перемещая тело из данного состояния в состояние, в котором

потенциальная энергия тела равна нулю.

Потенциальную энергию можно представить как энергию, запа-

сенную для дальнейшего использования.

Например, работа перемещения тела под действием силы тяже-

сти зависит лишь от разности высот h перемещаемого тела и не зави-

сит от формы траектории движения: A

1–2

= m g (h

1

– h

2

).

Если считать, что потенциальная энергия равняется нулю при

высоте h

2

= 0, то потенциальная энергия под действием силы тяжести:

W

п

(h) = m g h.

Здесь m – масса тела, g – ускорение свободного падения, h – вы-

сота тела относительно уровня, где потенциальная энергия считается

равной нулю.

Из определений кинетической и потенциальной энергий следует,

что единица измерения энергии совпадает с единицей измерения ра-

боты: [W] = [A] = Дж.

Потенциальная энергия упругодеформированного тела

W

п

= kx

2

/2,

где k – коэффициент упругости, х – абсолютная деформация.

Удар



это кратковременное контактное взаимодействие тел.

Абсолютно упругим называется удар, в результате которого

сохраняется суммарная кинетическая энергия тел.

14

Пусть v

1

, v

2

 скорости шаров с массами m

1

и m

2

до удара; u

1

, u

2

–

скорости после удара (рис. 10). Непосредст-

венно при ударе потенциальная энергия шаров

не изменяется. Поэтому сумма кинетических

энергий шаров после удара равняется сумме

кинетических энергий до удара:

2

11

vm

+

2

22

vm

=

2

11

um

+

2

22

um

.

Для системы из двух шаров закон сохранения импульса:

m

1

v

1

+ m

2

v

2

= m

1

u

1

+ m

2

u

2

.

Удар называется центральным, если до удара центры инерции тел

двигались по одной прямой. Тогда и после удара центры инерции бу-

дут двигаться вдоль этой же прямой. Для такого удара векторное

уравнение закона сохранения импульса вдоль этой прямой можно за-

писать в алгебраической форме.

Из системы уравнений законов сохранения кинетической энергии

и импульса можно получить формулы для скоростей шаров после

центрального удара:

u

1

=

21

22121

2)(

mm

mmm





vv

; u

2

=

21

11212

2)(

mm

mmm





vv

.

Абсолютно неупругим называется удар, в результате которого

скорости соударяющихся тел становятся одинаковыми и они дви-

жутся как одно целое со скоростью u

(рис.11). При таком ударе закон сохранения

механической энергии не выполняется. Часть

механической энергии затрачивается на ра-

боту деформации шаров и выделяется в виде

теплоты. Закон сохранения импульса выпол-

няется:

m

1

v

1

+ m

2

v

2

= (m

1

+ m

2

)u .

Отсюда скорость шаров после удара:

u =

21

2211

mm

m



v

.

Надо иметь в виду, что это векторное выражение.

Теплота, которая выделяется при неупругом ударе, равняется

разности кинетических энергий шаров до и после удара:

15

m

1

u

1

v

1

m

1

v

2

m

2

m

2

u

2

Рис. 10

m

1

v

1

(m

1

+m

2

)

v

2

u

m

2

Рис. 11

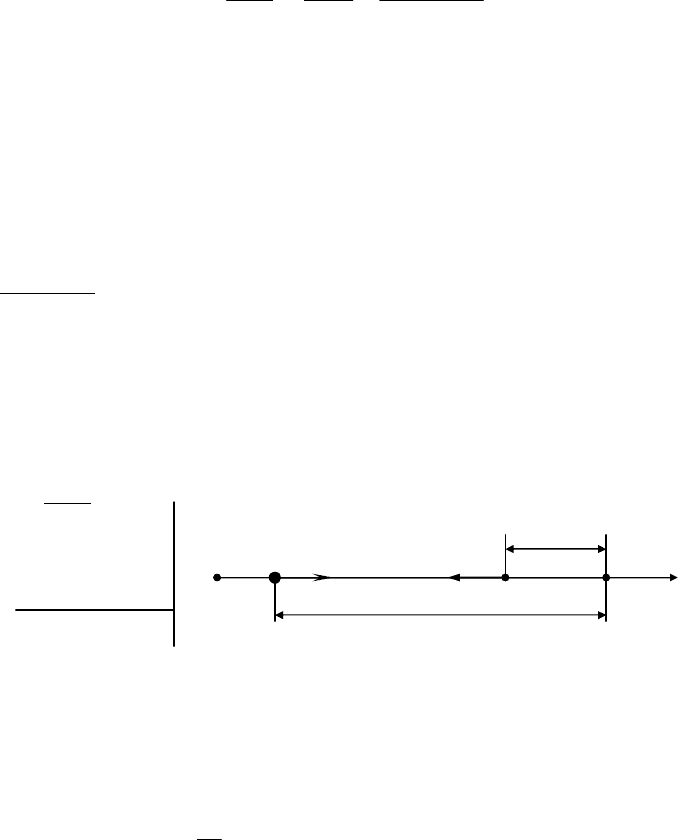
Q =

2

11

vm

+

2

22

vm



2

)(

2

21

umm 

Второй закон Ньютона в неинерциальных системах отсчета

m a = F + F

ин

,

где F  равнодействующая реальных сил; a  ускорение тела относи-

тельно неинерциальной системы; F

ин

 равнодействующая сил инер-

ции. Силы инерции вызваны ускоренным движением системы отсчета

и направлены противоположно ускорению системы а

о

:

F

ин

=  m а

о

.

1.2. Примеры решения и оформления задач

Пример 1.

Материальная точка массой m = 10 г движется вдоль горизон-

тальной прямой и ее координата с течением времени меняется соглас-

но закону x = a + bt + ct

2

. Здесь, а = 5 м, b = 20 м/c, c =  5 м/c

2

. Опре-

делить мгновенные скорости частицы в моменты времени t

1

= 1 c и

t

2

= 4 c, силы, действующие на частицу в данные моменты времени,

среднюю путевую скорость в промежутке времени от t

1

до t

2

.

Анализ:

В начальный момент времени t

o

= 0 частица находится в точке с

координатой х

о

= 5 м, как показано на рисунке.

Мгновенная скорость частицы в любой момент времени опреде-

ляется как первая производная от радиус-вектора частицы по времени.

По условиям задачи частица движется вдоль координатной оси х. По-

этому в данном случае мгновенная скорость совпадает с составляю-

щей скорости вдоль данного направления:



= 

dt

dx

x = (5 + 20t – 5t

2

) = 20 – 10t.

16

Дано

:

m =10г =0,01кг

x = 5+20t–5t

2

t

1

= 1 c

t

2

= 4 c



1

,



2

, F

1

,F

2

,



ср

S

1

0 t

o

v

o

F t

1

t

п

х

t

2

S

2

Силу, действующую на частицу, можно определить по второму

закону Ньютона: F = ma. Ускорение определяем, взяв производную от

выражения для мгновенной скорости по времени: а =



 = (20 – 10t) =

= 10 м/c

2

.

Как видно ускорение от времени не зависит и имеет отрицатель-

ное значение. Это говорит о том, что ускорение направлено противо-

положно направлению оси х и начальному направлению скорости,

поэтому через некоторое время от начала движения направление дви-

жения изменится. Это произойдет в момент времени t

п

, когда скорость

будет равняться нулю. Данный момент времени можем найти, при-

равняв выражение для скорости нулю:

20 – 10t

п

= 0, отсюда t

п

= 20/10 = 2 с.

Значит, общий путь будет равняться сумме путей в прямом S

1

и в

обратном S

2

направлениях: S = S

1

+ S

2

.

Средняя скорость по пути определяется как отношение общего

пути S к промежутку времени t = t

2

– t

1

, в течение которого этот путь

пройден:



ср

= S /t.

Анализ размерности:

Как видно из условия задачи коэффициенты в уравнении движе-

ния частицы являются размерными величинами, которые обеспечива-

ют единицу измерения координаты частицы в метрах: [х] = м.

[] = [х] /[t] = м/с. [F] = [m][a] = кгм/с

2

= Н(ньютон).

Решение:



1

=20 – 10t

1

= 20 – 101 = 10 м/с.



2

=20 – 10t

2

= 20 – 104 = - 20 м/с.

F

1

= F

2

= ma = 0,01(–10) = - 0,1 H.

S

1

= x(t

п

) – х(t

1

) = 5+20t

п

–5t

2

п

– (5+20t

1

–5t

2

1

) = 5 м.

S

2

= x(t

п

) – х(t

2

) = 5+20t

п

–5t

2

п

– (5+20t

2

–5t

2

) = 20 м.



ср

= S/t =(S

1

+ S

2

)/(t

2

– t

1

) = (5 + 25)/(4 – 1) = 10 м/с.

Ответ:

Мгновенная скорость в момент времени t

1

= 1 с:



1

=10 м/с.

Мгновенная скорость в момент времени t

2

= 4 с:



2

= –20 м/с.

Сила, действующая на частицу: F

1

= F

2

= 0,1 H. Сила направлена

противоположно направлению начальной скорости.

Средняя скорость по пути за промежуток времени за промежуток

времени от t

1

до t

2

:



ср

= 10 м/с.

17

Пример 2.

Автомобиль массой М = 3 т, двигаясь с постоянной скоростью



= 61,2 км/ч, начал экстренное торможение и остановился, проехав

путь l = 50 м. Определить результирующую силу трения, действую-

щую на колеса автомобиля. Удержится ли на месте груз, находящийся

на кузове автомобиля, если коэффициент трения груза о днище кузова



= 0,2? Если колесо автомобиля приближенно представить в виде

сплошного диска массой m = 50 кг, то какой кинетической энергией

обладало одно колесо до начала торможения? Сколько оборотов сде-

лает колесо до полной остановки, если радиус колеса R = 34 см.

Дано: Анализ:

М = 3т = 3000 кг



=61,2 км/ч =

3600

61200

= 17м/с

l = 50 м



= 0,2

R = 34 см = 0,34 м

m = 50 кг

F

тр

, W, F

тр2

, W

к

, N

Предположим, что автомобиль тормозится с постоянным ускоре-

нием а. Тогда формула для тормозного пути

l =



t



2

at

. (1)

В этой формуле неизвестно время торможения t. Для его опреде-

ления воспользуемся формулой для скорости при равнопеременном

движении



к

=



+ at, так как конечная скорость равняется нулю



к

= 0: t =



/a. Подставим это выражение в формулу (1):

l = 

а

2



+

а

2



= 

а

2



.

Отсюда получаем формулу для ускорения а = 

l2

2



.

Численное значение ускорения получается отрицательным, т.к. авто-

мобиль тормозится. Значение силы торможения можно определить

18

N

F

тр2

a m

г

F

тр

F

т

v

R

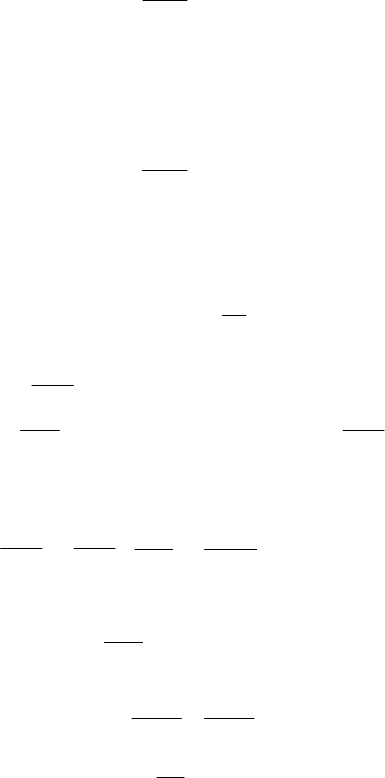
из второго закона Ньютона. Во время торможения на автомобиль дей-

ствуют только силы трения колес, поэтому

F

тр

= Ma = 

l

М

2



.

Если груз, находящийся в кузове автомобиля не скользить отно-

сительно автомобиля, то будет замедляться с таким же ускорением а,

что и автомобиль. Силой торможения для груза массой m

г

является

сила трения, значение которой можно определить по второму закону

Ньютона

F

т

= m

г

a = 

l

m

2



г

.

Максимальное значение силы трения F

тр2

=







m

г

g. В данном

случае на груз в вертикальном направлении действуют только сила

тяжести F

т

= m

г

g и сила реакции опоры N, поэтому N = m

г

g .

Груз не будет скользить, если выполнится условие

F

тр2

 F

т

или



g 

l2

2



.

Катящееся колесо обладает как кинетической энергией поступа-

тельного движения W

кп

=

2



m

, так и кинетической энергией враща-

тельного движения W

к

вр

=

2



J

. Момент инерции диска J =

2

mR

.

Угловая скорость колеса связана со скоростью поступательного

движения



= /R (предполагаем, что колесо не скользит на дороге).

В результате полная кинетическая энергия колеса

W

к

=

2



m

+

2

mR



2

R



=

4

2



3m

.

Число полных оборотов колеса можно найти, разделив тормоз-

ной путь на длину окружности обода колеса

N =

R

l



2

.

Анализ размерности:

[F

тр

] = [M][]

2

/[l] = кг Н

с

мкг

м

с

м









22

2

[W

к

] = [m][]

2

= кг

2

с

м

= Дж

[N

] = [l

]/[R] = м/м – безразмерная величина.

19

Вафин Д.Б. Задания по физике

Подождите немного. Документ загружается.