Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 101

Решение краевых задач — методы, использующие

функции штрафа (VIII)

Снятие ограничений, наложенных на управление – 2

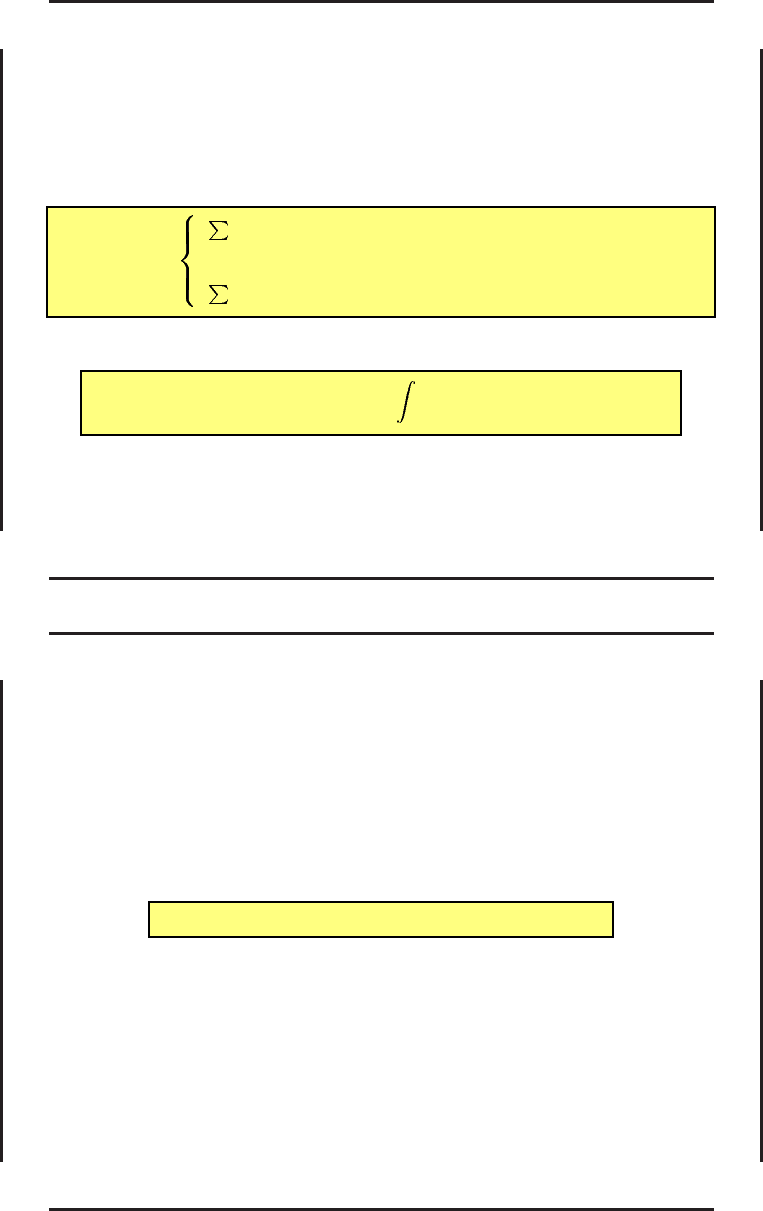
Введем в рассмотрение фу н кцию Ψ(u) следующим образом:

Ψ(u) =

i=1

− d

(2)

)

, если u

> d

(2)

0, если u

∈ [d

(1)

, d

(2)

i=1

− d

(2)

)

, если u

6 d

(1)

(94)

и будем решать задачу оптимального управления с функционалом

= J(x, y) +

Ψ(u)dt, (95)

но без ограничений на управление.

Данный метод можно и спользовать не только, когда ограничения на управления

имеют вид (93), но и в более общем случае.

Slide 102

Решение краевых задач — методы, использующие

функции штрафа (IX)

Снятие фазовых ог раничений – 1

Метод штрафных функций можно использовать и для снятия фазовых

ограничений

x(t) ∈ G

, t ∈ [t

, T ]. (96)

Для задач оптимального управления с фазовыми ограничениями можно получить

необходимые условия экстремума, как и для за дач без таких ограничений.

Однако эти условия получаются настолько сложными, что их трудно

использовать для построения эффективных вычислительных методов.

В то же время с помощью метода штрафных функций задачи данного класса

легко можно свести к более простым задачам.

Ю. В. Тюменцев 51

Оптимальное управление

Slide 103

Решение краевых задач — методы, использующие

функции штрафа (X)

Снятие фазовых ог раничений – 2

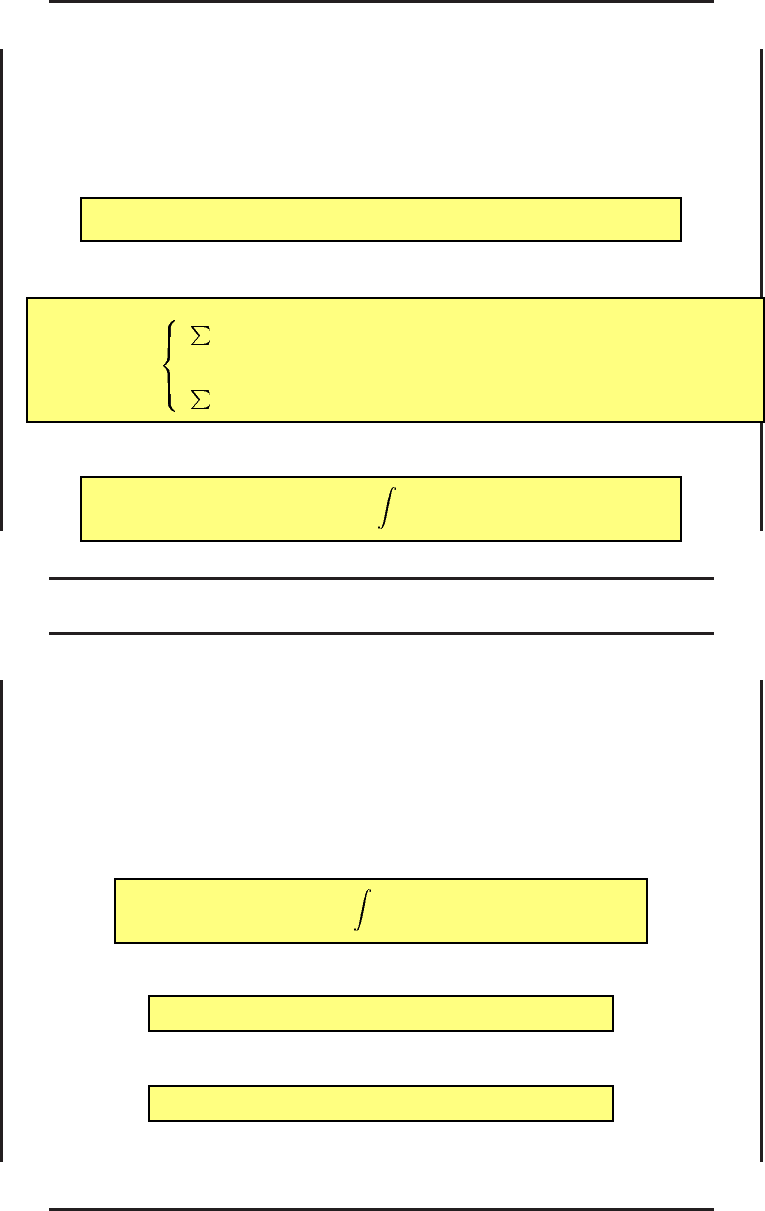
Пусть фазовые ограничения заданы в виде

(1)

(t) 6 x

(t) 6 ϕ

(2)

(t), i = 1, 2, . . . , l. (97)

Построим функцию Ψ

∗

(x), аналогичную функции (94):

∗

(u) =

i=1

(t) − ϕ

(2)

(t))

, если x

(t) > ϕ

(2)

(t),

0, если x

(t) ∈ [ϕ

(1)

(t), ϕ

(2)

(t)],

i=1

(t) − ϕ

(2)

(t))

, если x

(t) 6 ϕ

(1)

(t),

и вместо функционала J(x, y) будем минимизировать функционал

= J(x, y) +

∗

(x(t))dt.

Slide 104

Решение краевых задач — методы, использующие

функции штрафа (XI)

Снятие дифференциальных связей – 1

Рассмотрим задачу отыскания минимума функционала

J(x, u) =

F (x, u, t)dt (98)

при ограничениях (89)

˙x = f(x, u, t), x(t

) = x

Концы фазовой траектории будем считать фиксированными

x(t

) = x

, x(T ) = x

. (99)

Ю. В. Тюменцев 52

Оптимальное управление

Slide 105

Решение краевых задач — методы, использующие

функции штрафа (XII)

Снятие дифференциальных связей – 2

С дифференциальными связями можно поступить точно так же, как и с

ограничениями на управления и фазовые переменные, если ввести

соответствующим образом функции штрафа.

После выполнения указанных действий, придем к функционалу следующего

вида:

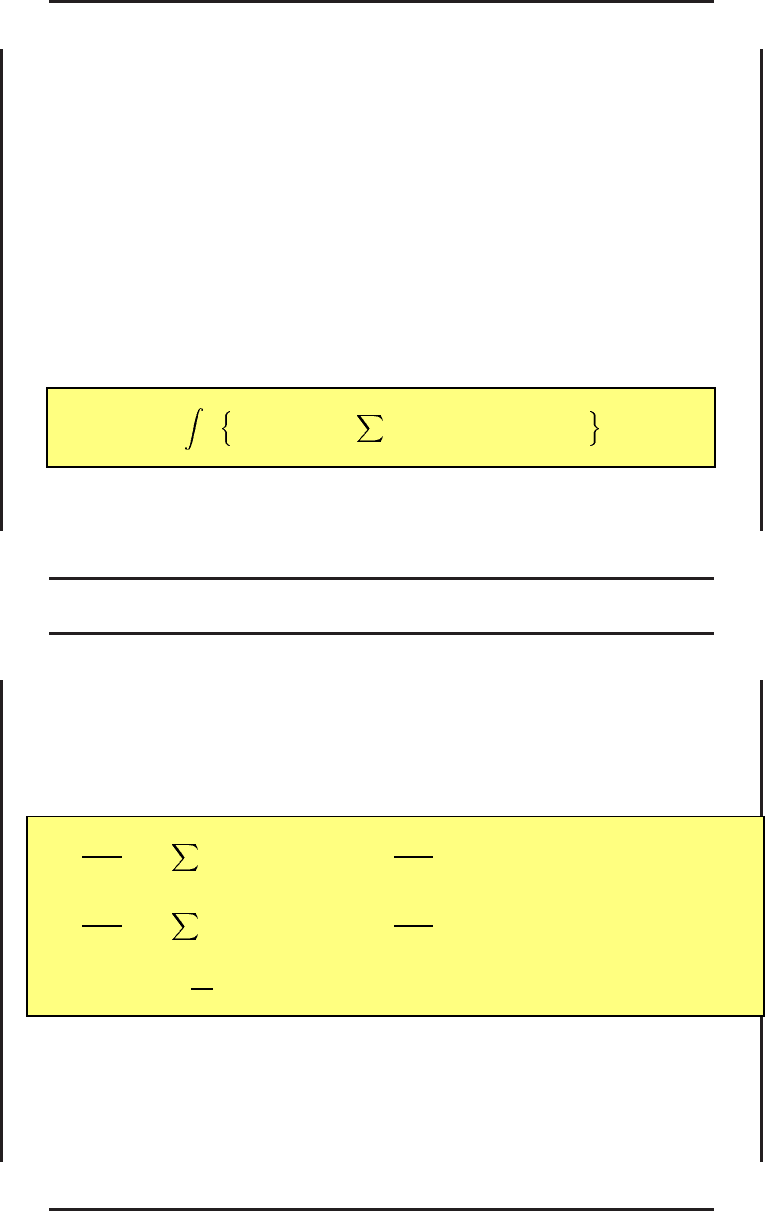
J(x, u) =

F (x, u, t) +

i=1

( ˙x

− f

(x, u, t))

dt. (100)

Slide 106

Решение краевых задач — методы, использующие

функции штрафа (XIII)

Снятие дифференциальных связей – 3

Составим для функционала (100) уравнения Эйлера:

∂F

∂u

− 2

i=1

( ˙x

− f

(x, u, t))

∂f

∂u

= 0, j = 1, 2, . . . , m,

∂F

∂x

− 2

i=1

( ˙x

− f

(x, u, t))

∂f

∂x

+ 2λ

( ˙x

− f

(x, u, t)) = 0, s = 1, 2, . . . , n,

(101)

Решение этой системы у ра внений имеет ту же степень трудности, что и системы,

получаемые при рассмотрении задачи Лагранжа.

Существуют также специализированные схемы ре шения данной задачи,

позволяющие более эффективно отыскивать решение для нее.

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 136–138)

Ю. В. Тюменцев 53

Оптимальное управление

Slide 107

Решение краевых задач — методы, использующие

функции штрафа (XIV)

Снятие дифференциальных связей – 4

Методы штрафных функций не позволяют получать точных решений.

Тем не менее, эти методы довольно популярны вследствие их «всеядности» и

относительной простоты численной реализации.

Если при расчете оптимальной программы требования к точности выше того

предела, который можно обеспечить с помощью метода штрафных функций, тогда

решение, полученное с его помощью, можно использовать в качестве хорошего

начального приближения для более точных и сложных методов.

Slide 108

Прямые методы теории оптимального управления

Общая характеристика

Прямые методы вариационного исчисления — все те методы расчета

экстремалей, которые непосредственно не используют необходимых условий.

Пример — метод Ритца.

Схема метода: требуется отыскать минимум функционала J(y), y ∈ Y , где Y

— некоторое множество, например, множество дифференцируемых функций.

Решение задачи отыскивается в виде

y =

i=1

, ϕ

∈ Y.

Задача определения постоянных λ

сводится к решению сис т е мы уравнений:

∂J(λ

, λ

, . . . , λ

)

∂λ

= 0, i = 1, 2, . . . , N.

Основные прямые методы, которые нашли применение в практике расчета

оптимальных программ, основываются на редукции исходной вариационной

задачи к некоторой конечномерной задаче.

Чаще всего эти методы используют идеи нелинейного программир ования, а

также последовательного анализа вариантов.

Ю. В. Тюменцев 54

Оптимальное управление

Slide 109

Конечномерные аналоги задач оптимального

управления (I)

Предварительные замечания

Два вида взаимосвязей между задачами оптимального у правления и задачами

нелинейного программирования:

1. Если заменить дифференциальный оператор в вариационной зада-

че на конечно-разностный, то вместо исходной задачи оптимального

управления получаем некоторую задачу н елинейного программирова-

ния.

2. Многие задачи линейного и нелинейного программи рования, стати-

ческие по существу, можно интерпретировать как многош аговые

динамические процессы, описываемые уравнениями ти па конечно-

разностных, что позволяет использовать аппарат теории оптимального

управления.

В нелинейном программировании в конечномерных пространствах достигнуты

значительные успехи как в теоретиче ской области, так и в вычислительном

аппарате, поэтому вполне оправданным является стремление использовать

аппарат НЛП в задачах оптимального управления.

Применению НЛП в оптимальном управлении способствует то, что задачи НЛП,

возникающие при дискретизации задач оптимального управления, обладают рядом

специфических черт, позволяющих эффективно применять процедуры НЛП.

Slide 110

Конечномерные аналоги задач оптимального

управления (II)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 1

Два подхода к редукции задачи оптимального управления к задаче НЛП:

❑ получить задачу НЛП с целевой функцией, которая

зависит от у п равлений;

❑ получить задачу НЛП с целевой функцией, которая

зависит от состояний системы.

Каждый из этих способов имеет свои достоинства и недостатки.

Ю. В. Тюменцев 55

Оптимальное управление

Slide 111

Конечномерные аналоги задач оптимального

управления (III)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 2

Пусть для определенности речь идет об отыскании минимума функционала

J(x, u) =

F (x, u)dt, (102)

при условии, что векторы x и u связаны дифференциальным уравнением

˙x = f(x, u). (103)

В пространстве x, t проведем гиперплоскости

t = iτ,

где τ — шаг численного интегрирования. Примем, что на интервале

(iτ, (i + 1 )τ) управляющая вектор-функция принимает пост оянное значение,

равное u

Slide 112

Конечномерные аналоги задач оптимального

управления ( IV)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 3

Заменим уравнение (103) разностной схемой

i+1

= x

+ τf(x

, u

). (104)

Соответственно, интеграл (103 ) заменится следующей интегральной суммой:

J(x

, u

) = τ

N −1

i=0

F (x

, u

). (105)

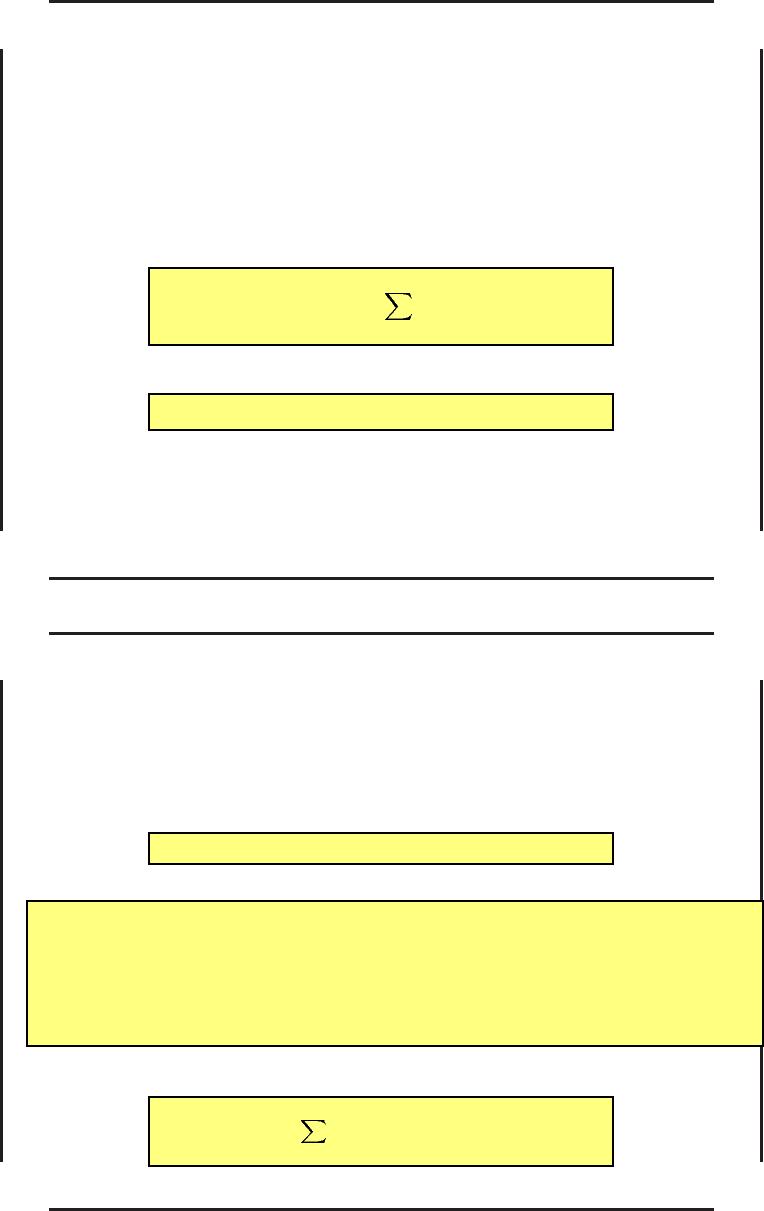
Это простейш ая схема раз н остной аппроксимации первого порядка точности.

Вместо схемы (104), (105) можно взять любую другую, в том числе и более

высокого порядка точности.

Ю. В. Тюменцев 56

Оптимальное управление

Slide 113

Конечномерные аналоги задач оптимального

управления ( V)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 4

Итак, в результате конечно-разностной аппроксимации получена следующая

задача теории систем с дискретным временем: определить векторы u

и x

доставляющие минимум с умме (105)

J(x

, u

) = τ

N −1

i=0

F (x

, u

)

при связях (104)

i+1

= x

+ τf(x

, u

)

и условиях u

∈ G

, x

∈ E

, x

∈ E

, где G

, E

и E

— некоторые

заданные множества.

Эта задача уже является задачей конечномерного нели нейного

программирования.

Slide 114

Конечномерные аналоги задач оптимального

управления ( VI)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 5

Полученной формулировке задачи можно придать несколько другой вид.

Пусть начальное состояние системы (вектор x

) фиксировано, тогда равенство (104)

i+1

= x

+ τ f(x

, u

позволяет последовательно исключить фазов ы е векторы

= x

+ τ f(x

, u

) = Φ

= Φ

) + τ f (Φ

), u

) = Φ

, u

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

= Φ

k−1

, . . . , u

k−2

) + τ f (Φ

k−1

, . . . , u

k−2

), u

k−1

) =

= Φ

, . . . , u

k−1

)

(106)

Функционал (105) становится после выполнения этих опе раций только фу нкцией векторов

, . . . , u

N −1

J =

N −1

i=0

, u

, . . . , u

), (107)

где I

, u

, . . . , u

) = τ F (Φ

, . . . , u

i−1

), u

Ю. В. Тюменцев 57

Оптимальное управление

Slide 115

Конечномерные аналоги задач оптимального

управления ( VII)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 6

Таким образом, з адача оптимального управления сведена к минимизации

некоторой функции конечного числа переменных.

При этом получена задача специального вида и ее специфику можно

использовать для упрощения процесса получения решения.

А именно, функция J —это сумма конечного числа слагаемых I

, причем каждое

из этих слагаемых зависит только от первых i неизвестных.

Эта особенность позволяет и спользовать для отыскания минимума фу нкции

аппарат последовательного анализа вариантов.

Slide 116

Конечномерные аналоги задач оптимального

управления ( VIII)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 7

Условие на правом конце также может быть выражено как функци я векторов

, . . . , u

N −1

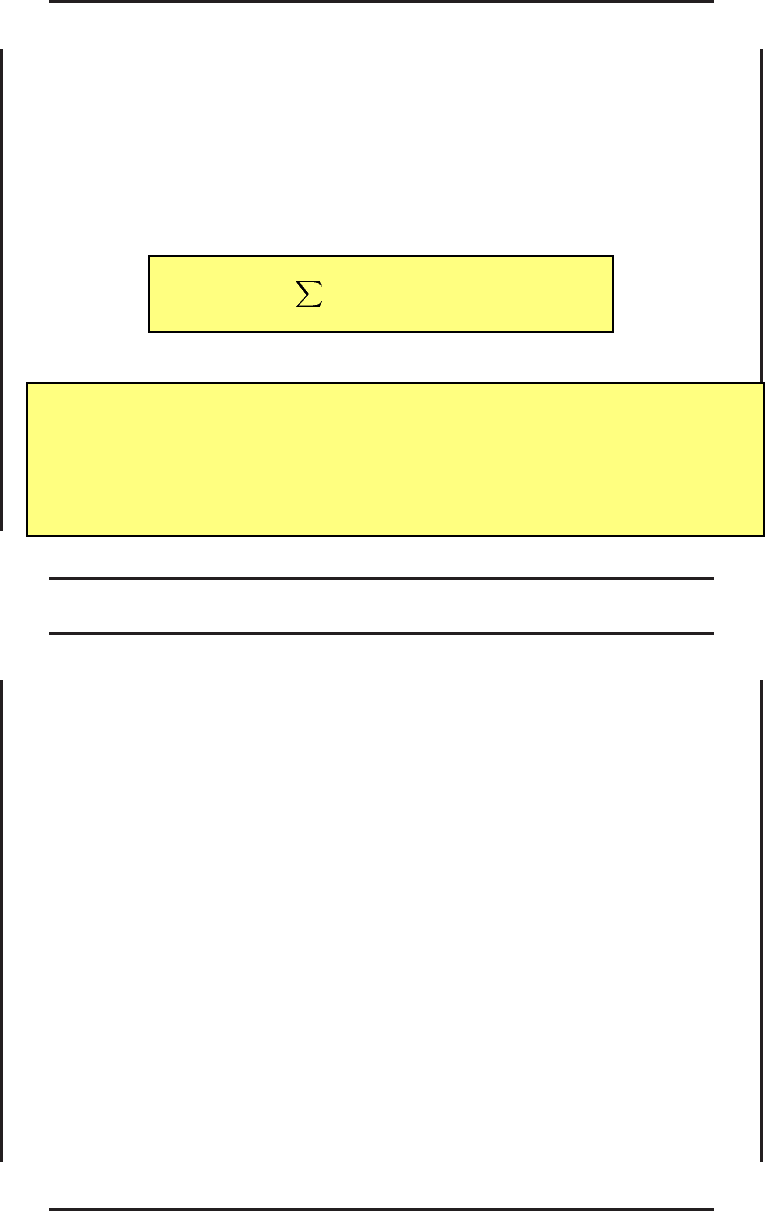
Например, если конечное значение вектора x, т.е. вектор x

, фиксировано, то

имеет место соотношение

= Φ

, u

, . . . , u

N −1

). (108)

Поскольку значение вектора x

задано, то (108) — это некоторое условие типа

равенства, наложенное на искомые величины u

, u

, . . . , u

N −1

Ю. В. Тюменцев 58

Оптимальное управление

Slide 117

Конечномерные аналоги задач оптимального

управления (IX)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 8

Если мы имеем задачу без фазовых о граничений, то исходная задача Лагранжа

формулируется теперь следующим образ ом: требуется определить векторы

, u

, . . . , u

N −1

, доставляющие м инимум функции (107)

J =

N −1

i=0

, u

, . . . , u

при условии u

∈ G

и условиях (1 06)

= x

+ τf(x

, u

) = Φ

= Φ

) + τf(Φ

), u

) = Φ

, u

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

= Φ

k−1

, . . . , u

k−2

) + τf(Φ

k−1

, . . . , u

k−2

), u

k−1

) =

= Φ

, . . . , u

k−1

)

Slide 118

Конечномерные аналоги задач оптимального

управления (X)

Простейший способ сведения задачи оптимального

управления к задаче нелинейного программирования – 9

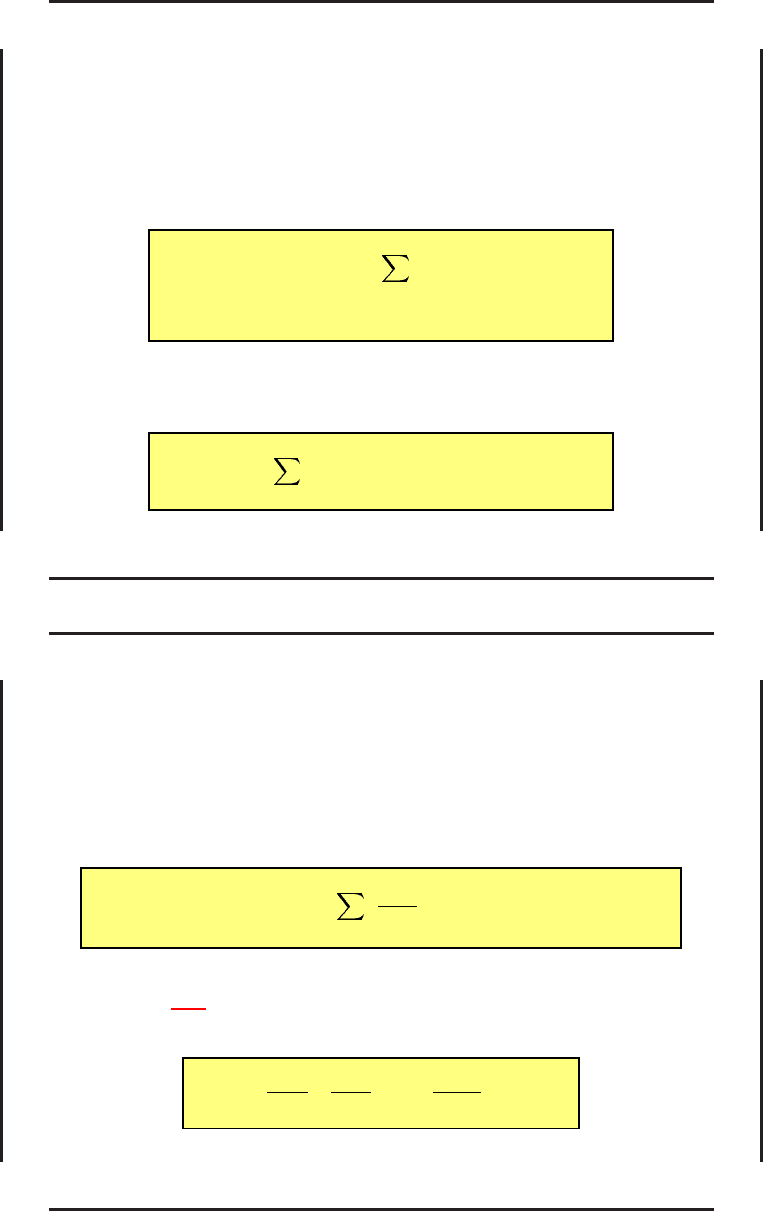
Сформулированная задача уже является некоторой задачей нелинейного

программирования и для ее решения можно использовать разнообразные

методы НЛП.

Выбор конкретного метода численного решения задачи НЛП определяется

обычно природой функций J(u) и Φ

(u).

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 158–162)

Ю. В. Тюменцев 59

Оптимальное управление

Slide 119

Методы нелинейного программирования в задачах

оптимального управления (I)

Метод градиентного спуска в случае простейшей разностной

аппроксимации – 1

Рассмотрим конечномерную задачу (105), (104):

J(x

, u

) = τ

N −1

i=0

F (x

, u

i+1

= x

+ τf(x

, u

Будем считать для простоты, что левый конец фазовой траектории фиксирован.

Как было показано, данная задача сводится к ми нимизации функции вида

J =

N −1

i=0

, u

, . . . , u

), (109)

где u

— векторы размерности m, значения которых требуется найти.

Slide 120

Методы нелинейного программирования в задачах

оптимального управления (II)

Метод градиентного спуска в случае простейшей разностной

аппроксимации – 2

Каждый шаг в методе градиентов сводится к расчету очередного приближенного

значения векторов u

по следующей формуле:

= ˜u

− κ

N −1

i=j

∂I

∂u

= ˜u

− κG

, (110)

где ˜u

— предыдущее приближение, κ > 0 — шаг градиентного спуска.

Здесь величины

∂I

∂u

— это производные скалярной функции по векторному

аргументу, т.е. они являются векторами с компонентами

∂I

∂u

∂I

∂u

, . . .

∂I

∂u

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 173–176)

Ю. В. Тюменцев 60