Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 81

Решение краевых задач — перенос граничных

условий (III)

Линейные задачи с квадратичным функционалом – 2

Сформулируем две задачи для рассматриваемой системы.

Задача α. Найти управление, переводящее систему (70) за время T из состояния

(72) в состояние

x(T ) = x

. (73)

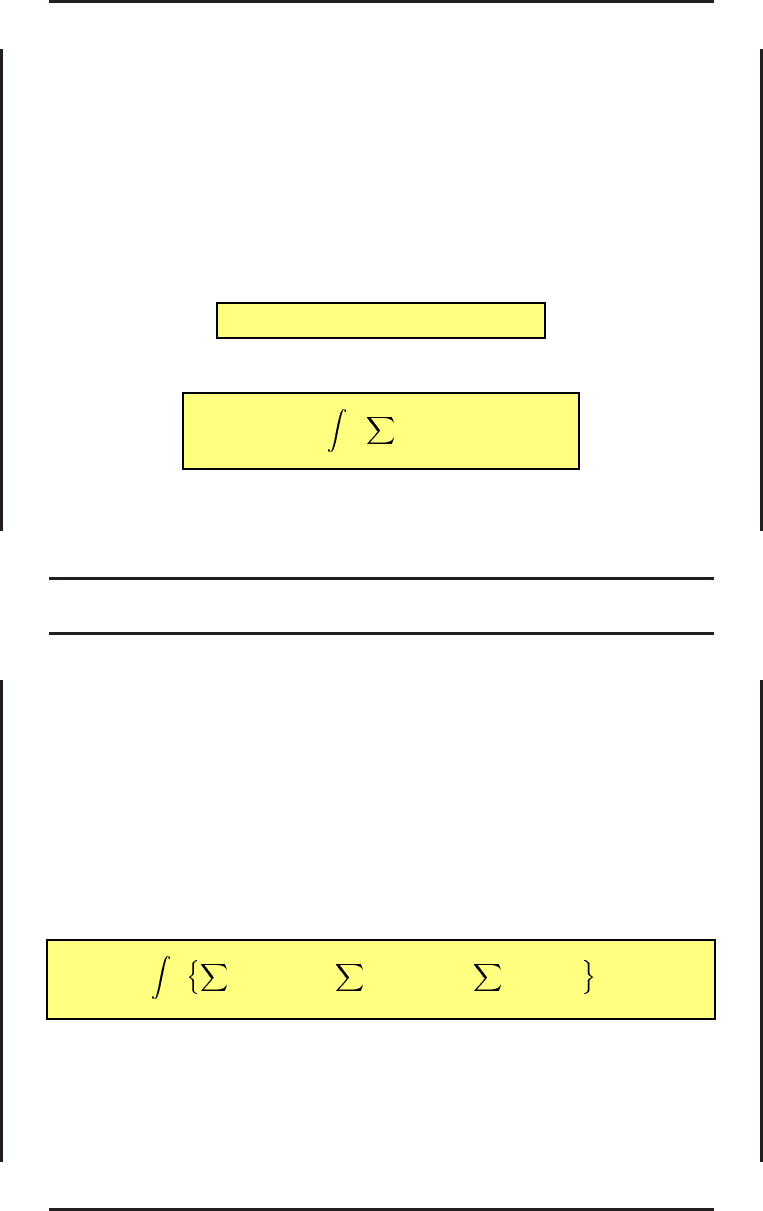
так, чтобы функционал

J =

)

dt. (74)

принимал на оптимальной траектории минимальное значение.

Slide 82

Решение краевых задач — перенос граничных

условий (IV)

Линейные задачи с квадратичным функционалом – 3

Задача β. Найти управление, переводящее систему ( 70) за время T из состояния

(72) в состояние (73) так, чтобы функционал

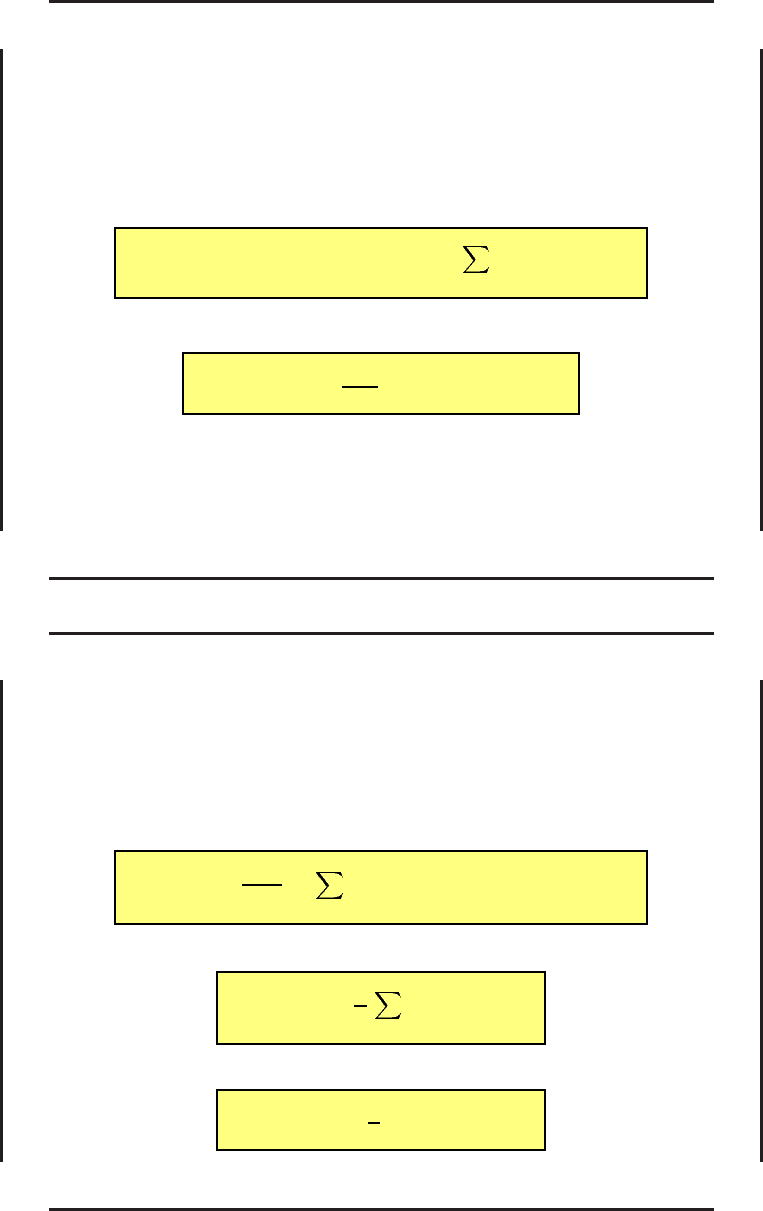
J =

i,j

dt (75)

достигал на оптимальной траектории своего наиме ньшего значения.

Функционал (74) является, очевидно, частным случаем функционала (75).

Ю. В. Тюменцев 41

Оптимальное управление

Slide 83

Решение краевых задач — перенос граничных

условий (V)

Линейные задачи с квадратичным функционалом – 4

Рассмотрим вначале задачу α. Составим для нее функцию Гамильтона

h = (Ax, ψ) + ( Bu, ψ) −

)

. (76)

Уравнение для импульсов будет иметь следующий вид:

ψ = −

∂H

∂x

= −A

∗

ψ. (77)

Здесь A

∗

означает транспонированную матрицу.

Заметим, что уравнение (77) может быть проинтегрировано независимо от

уравнения (70) .

Slide 84

Решение краевых задач — перенос граничных

условий (VI)

Линейные задачи с квадратичным функционалом – 5

Для определения управления вычислим

∂H

∂u

− 2u

= 0,

откуда

или

u =

∗

ψ. (78)

Ю. В. Тюменцев 42

Оптимальное управление

Slide 85

Решение краевых задач — перенос граничных

условий (VII)

Линейные задачи с квадратичным функционалом – 6

Подставляя (78 ) в (70), получим

˙x = Ax +

Bψ, (79)

где

B =

∗

Итак, задача α свелась к краевой задаче для системы линейных

дифференциальных уравнений (77) и (79), порядок которой ра вен 2n.

Slide 86

Решение краевых задач — перенос граничных

условий (VIII)

Линейные задачи с квадратичным функционалом – 7

Совершенно аналогично рассматривается и общий случай квадратичного

функционала, т.е. задача β:

H = (Ax, ψ) + (Bu, ψ) − (x, Cx) − (x, Du) − (u, Eu), (80)

где C, D и E — матрицы, фи гурирующие в (75).

Ю. В. Тюменцев 43

Оптимальное управление

Slide 87

Решение краевых задач — перенос граничных

условий (IX)

О переносе граничных условий – 1

Линейные уравнения — это единственный класс дифференциальных уравнений,

для которых разработаны регулярные методы решения краевых задач.

Рассмотрим уравнение

˙x = Ax + f. (81)

Пусть элементы матрицы A (величины a

) — некоторые фу нкции времени.

Методы решения краевых задач для уравнения (81) основаны на идее переноса

граничных условий из одной точки в другую.

Slide 88

Решение краевых задач — перенос граничных

условий (X)

О переносе граничных условий – 2

Пусть вектор-функция x(t) (решение уравнения (81)) удовлетворяет условию

, x(t

)) =

· x

) = α

. (82)

Будем говорить, что условие (82) пе ренесено из точки t

в точку t, если удается

так определить независимо от x вектор-функцию l(t) и скалярную функцию

α(t), удовлетворяющие условиям

l(t

) = l

, α(t

) = α

, (83)

что для любого момента t 6= t

(l(t), x(t)) = α(t).

Ю. В. Тюменцев 44

Оптимальное управление

Slide 89

Решение краевых задач — перенос граничных

условий (XI)

О переносе граничных условий – 3

Для выполнения требуемого переноса граничных условий можно использовать

сопряженное уравнение

l = −A

∗

l, (84)

где A

∗

— транспонированная матрица.

Умножим скалярно обе части уравнения (8 1) на l, а уравнения (84) — на x и

сложим. Тогда, так как

(Ax, l) = (x, A

∗

l),

мы получим

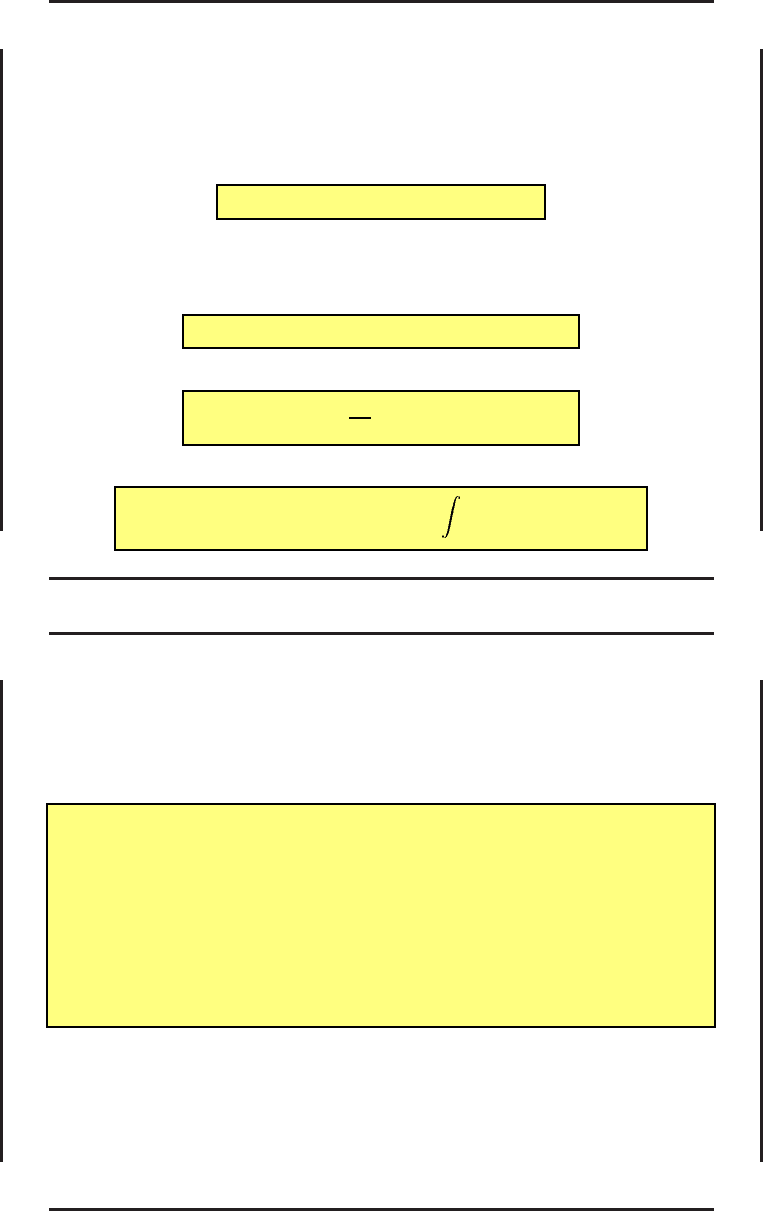
˙xl +

lx ≡

(l, x) = (l, f),

откуда

(l, x)

t=t

= (l, x)

t=t

(l, f)dt.

Slide 90

Решение краевых задач — перенос граничных

условий (XII)

О переносе граничных условий – 4

Таким образом, доказано следующее утверждение:

Теорема. Если l(t) — решение задачи Коши (8 3), (84), а функция α(t)

удовлетворяет у равнению

˙α = ( l, f) (85)

и условию

α(t

) = α

то вектор-функция x(t) для любых t удовлетворяет условию

(l(t), x(t)) = α(t). (86)

Эта теорема позволяет любое линейное краевое условие типа (82) перенести из

точки x

в любую точку.

Для этого достаточно решить одну задачу Коши для сопряженной системы и

одну задачу Коши для скалярного уравнения (85).

Таким образом, получена возможность любую краевую задачу с условия типа

(82) свести к задаче Коши путем переноса всех граничных условий в одну точку.

Ю. В. Тюменцев 45

Оптимальное управление

Slide 91

Решение краевых задач — перенос граничных

условий (XIII)

О переносе граничных условий – 5

Несмотря на логическую простоту полученного результата, компьютерная

реализация описанной процедуры может встретить значительные трудности.

Это связано с возможностью встретиться с быстрорастущими решениями, как

это видно из следующего примера.

Пример. Пусть исходное ура внение — скалярное, имеющее вид:

˙x = −ax + f, a(t) > 0,

тогда сопряженное уравнение

l = al будет иметь экспоненциально растущее

решение. В этом случае говорят, что процедура переноса граничных условий

является неустойчивой.

Существуют методы, позволяющие избежать трудностей, связанных с

существованием быстрорастущих функций l(x)

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 97–99)

Они позволяют сделать процедуру переноса граничных условий (ее называют

также прогонкой) устойчивой.

При этом, однако, в отличие от ранее рассмотренного случая, приходится решать

задачу Коши уже для нелинейных дифференциальных уравнений. Такой

переход практически не усложняет процедуру численного решения.

Slide 92

Решение краевых задач — перенос граничных

условий (XIV)

О переносе граничных условий – 6

Итак, решение краевой задачи сводится к решению ряда задач Коши.

Решение краевой задачи методом прогонки осуществляется по следующей общей

схеме.

Сначала все данные задачи Коши перегоняются с левого конца траектории на

правый конец и эта процедура всегда устойчива.

Далее, решается задача Коши справа налево для системы (81) :

˙x = Ax + f.

Эта процедура может оказаться неустойчивой.

В таком случае следует перегнать сначала все условия Коши справа налево (эта

процедура всегда устойчива), а затем решать задачу Коши для системы (81) слева

направо.

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 97–104)

Ю. В. Тюменцев 46

Оптимальное управление

Slide 93

Решение краевых задач — перенос граничных

условий (XV)

О переносе граничных условий – 7

Как уже отмечалось, метод решения краевых задач, использующий перенос

граничных условий, ча сто называют методом прогонки.

Это название соответствует харак теру процедуры: сначала грани чные условия

переносятся с одного конца траектории на другой, для этого приходится решать

задачу Коши, интегрируя уравнения, например, слева направо, потом остается

решить еще одну задачу Коши, причем в этом случае потребуется

проинтегрировать систему справа налево.

Метод прогонки используется и для решения нелинейных краевых задач.

В этом случае строятся итерационные процедуры, на каждом шаге которых

надо решать краевую задачу для линейных уравнений.

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 109–111)

Slide 94

Решение краевых задач — методы, использующие

функции штрафа (I)

Функции штрафа в задачах об относительном экстремуме – 1

При усложнении структуры ограничений ре зко усложняют ся необходимые

условия экстремума, а также и методы расчета, использующие эти необходимые

условия.

Разработано значительное число способов преодоления трудностей, вызванных

существованием сложных ограничений.

Один из таких способов — введение функций штрафа (штрафных функций).

Ю. В. Тюменцев 47

Оптимальное управление

Slide 95

Решение краевых задач — методы, использующие

функции штрафа (II)

Функции штрафа в задачах об относительном экстремуме – 2

Использование функций штрафа удобно пояснить на примере задачи отыскания

максимума дифференцируемой функции f(x), x ∈ R

при ограничениях

типа равенства

= 0, i = 1, 2, . . . , m < n, (87)

где ϕ

— также дифференцируемые функции.

Идея метода штрафных функций состоит в замене задачи отыскания

относительного максимума исходной функции задачей отыскания абсолютного

максимума функции

I(x) = f(x) −

i=1

[ϕ

(x)]

, (88)

где Λ

— некоторые положительные постоянные.

Выражения Λ

[ϕ

(x)]

называются штрафными функц и ями.

Slide 96

Решение краевых задач — методы, использующие

функции штрафа (III)

Функции штрафа в задачах об относительном экстремуме – 3

Если условия связи ϕ

= 0 выполнены, то, соответственно Λ

[ϕ

(x)]

= 0 и,

следовательно, I(x) = f( x).

Если условия связи не удовлетворены, т.е. ϕ

6= 0, тогда и Λ

[ϕ

(x)]

6= 0. В

этом случае слагаемое Λ

[ϕ

(x)]

в правой части (88) характеризует невязку —

меру отклонения точки x от гиперповерхности ϕ

= 0, i = 1, 2, . . . , m.

Величины штрафов Λ

влияют на процесс получения решения и характер

получаемого решения.

Р. Курант (1943) показал, что при Λ

→ ∞ точка x

∗

(Λ

), в которой функция I

достигает максимума, стремится к точке ˜x, в которой достигается относительный

максимум функции f(x) и при этом f(˜x) = I(˜x).

Ю. В. Тюменцев 48

Оптимальное управление

Slide 97

Решение краевых задач — методы, использующие

функции штрафа (IV)

Функции штрафа в задачах об относительном экстремуме – 4

Чем больше будут числа Λ

, тем больше будет штраф за нарушение условий

связи ϕ

= 0.

При малых Λ

метод штрафных функций дает большую погрешность.

Если же числа Λ

велики, то значения x

∗

и ˜x будут близки, но при расчетах

тогда придется оперировать большими числами, которые ум ножаются на малые

величины, что, в свою очередь, являетс я исто чником ошибок.

С помощью метода штрафных функций трудно получить высокую точность

решения, поэтому ча ще всего, решение, полученное этим методом, используют

как начальное п риближение для ка кого-либо другого метода, более точного, но

и более трудоемкого.

Slide 98

Решение краевых задач — методы, использующие

функции штрафа (V)

Задачи с ограничениями, наложенными на конец траектории

(1)

Метод штрафных функций довольно ши роко применяется для решения задач

оптимального управления.

Пусть требуется решить задачу Майера следующего вида.

Определить функ ц ии x(t), u(t), доставляющие максимум функционалу

F (x(T)) при ограничениях

˙x = f(x, u, t), x(t

) = x

, (89)

(x(T )) = 0, i = 1, 2, . . . , k < n, (90)

u = G

. (91)

Ю. В. Тюменцев 49

Оптимальное управление

Slide 99

Решение краевых задач — методы, использующие

функции штрафа (VI)

Задачи с ограничениями, наложенными на конец траектории

(2)

Применение к рассматриваемой задаче метода штрафных функций приводит к

замене исходного функциона ла F (x(T)) функционалом следующего вида:

J(x, u, λ) = F (x(T)) +

i=1

[ϕ

(x(T ))]

, (92)

где λ

> 0.

После этого вместо исходной задачи для функ ц ионала F (x(T)) решается

задача со свободным правым концом для фун кционала J(x, u, λ).

(См. подробнее: Моисеев Н.Н. Численные методы в теории оптимальных

систем. – М.: Наука, 1971. – с. 129–130, 134)

Slide 100

Решение краевых задач — методы, использующие

функции штрафа (VII)

Снятие ограничений, наложенных на управление – 1

Задачи оптимального управления зн ачительно легче решать, если устранить

ограничения на управления таким образом, чтобы уравнение

∂H

∂u

= 0

определяло управление как дифференцируемую функц ию фазовых координат и

импульсов. Тогда можно будет применить метод нелинейной прогонки.

Снять ограничения можно введением функций штрафа.

Пусть требуется отыскать минимум функционала J(x, u) при ограничениях

u = G

, которые для определенности запишем в виде

(1)

6 u

6 d

(2)

, i = 1, 2, . . . , m. (93)

Ю. В. Тюменцев 50