Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды
Подождите немного. Документ загружается.


Оптимальное управление
Slide 61
'
&
$
%
Простейшие способы решения краевых задач ( I)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 1
Необходимые условия (например, принцип максимума Понтрягина) позволяют
получить некоторую краевую задачу. Искомая экстремаль должна содержаться
среди решений этой краевой задачи.
Краевая задача для обыкновенных дифференциальных у равнений — нет хороших
алгоритмов ее непосредственного решения.
Фактически для таких уравнений мы умеем хорошо решать только задачу Коши.
Рассмотрим как пример задачу с фиксированным левым концом. Здесь на
левом конце мы имеем только n условий, хотя порядок системы равен 2n.
Проблема: Каким обра зом, используя наше умение решать задачу
Коши, построить решение краевой задачи?
Slide 62
'
&
$
%
Простейшие способы решения краевых задач ( II)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 2
Рассмотрим одну из возможност е й решения краевой задачи, используя наше
умение решать задачу Коши.
Пусть требуется отыскать упр авление u(t), которое переводит систему
˙x = f(x, u, t) (63)
за время T − t
0
из одного фиксированного состояния x
0
в другое
фиксированное состояние x
T
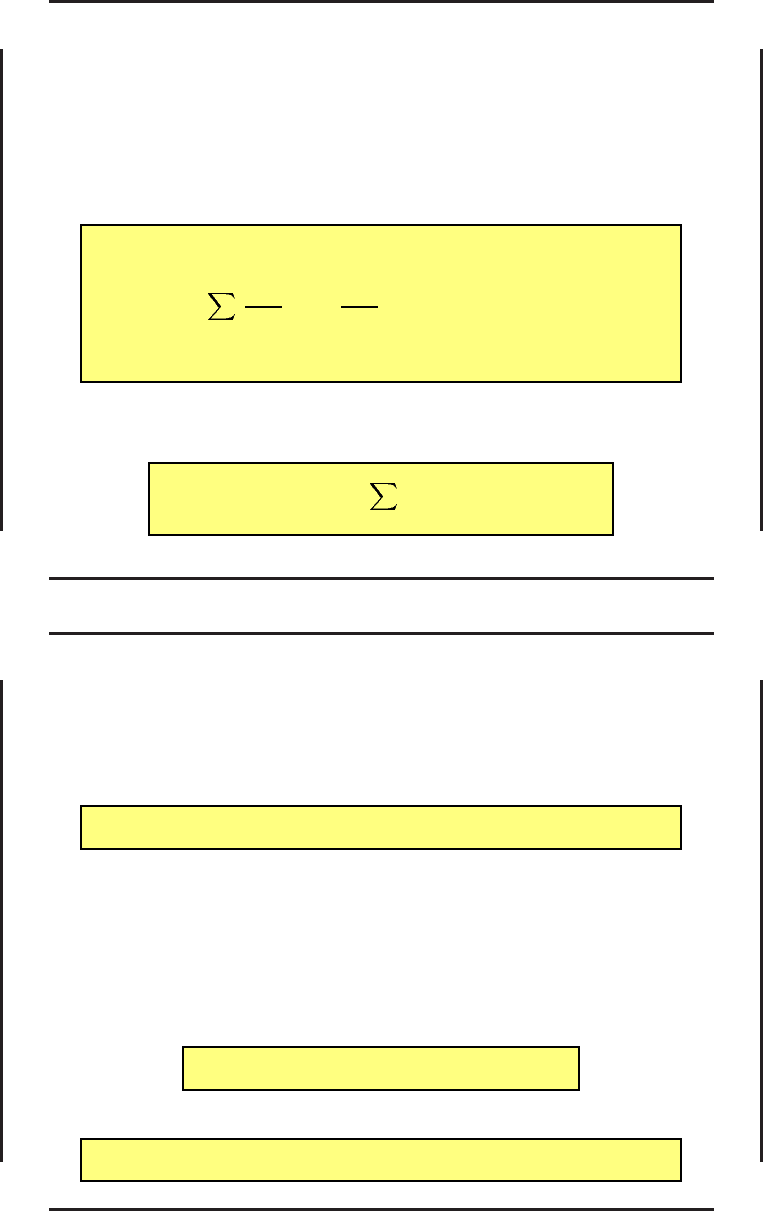
при условии, что интеграл
J(x, u) =
T
t
0
F (x, u, t)dt (64)
принимает минимальное значение.
Ю. В. Тюменцев 31
Оптимальное управление
Slide 63
'
&
$
%
Простейшие способы решения краевых задач ( III)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 3
Рассматриваемая задача сводится к отысканию функций x
1
, . . . , x
n
,
ψ
1
, . . . , ψ
n
, удовлетворяющих системе уравнений
˙x
i
= f
i
(x
1
, . . . , x
n
, u
1
, . . . , u
m
, t),
˙
ψ
i
= −
n
j=1
∂f
j
∂x
i
ψ
j
+
∂F
∂x
i
=
= ϕ
i
(x
1
, . . . , x
n
, u
1
, . . . , u
m
, t, ψ
1
, . . . , ψ
n
),
(65)
где u = u(x, ψ, t) в каждый момент определяется из условия максимума
функции Гамильтона (56):
H = (ψ, f) =
n
i=0
ψ
i
f
i
(x, u, t).
Slide 64
'
&
$
%
Простейшие способы решения краевых задач (IV)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 4
Решение системы (65) должно удовлетворять 2n условиям
x
i
(t
0
) = x
0
i
, x
i
(T) = x
T
i
, i = 1, 2, . . . , n. (66)
Чтобы построить интегральную кривую системы (65), следует тем или иным
способом задать n чисел ψ
i
(t
0
) = α
i
.
Построив по значениям x
0
i
и α
i
траекторию системы (65), получим при t = T
некоторые значения фазовых координат ˜x
i
(T). В общем случае они, конечно, не
будут равны x
i
(T ).
Введем невязки
X
i
= ˜x
i
(T) − x
T
i
.
Эти невязки будут, очевидно, функциями начальных з н ачений импульсов α
i
:
X
i
= X
i
(α
1
, α
2
, . . . , α
n
), i = 1, 2, . . . , n. (67)
Ю. В. Тюменцев 32

Оптимальное управление
Slide 65
'
&
$
%
Простейшие способы решения краевых задач ( V)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 5
Чтобы решить поставленную задачу отыскания оптимальной программы, требуется
найти числа α
1
, α
2
, . . . , α
n
, которые обращают функции X
i
в нули.
Итак, исходная вариационная задача сведена к задаче отыскания нулей функций
X
i
(α
1
, . . . , α
n
).
Следует подчеркнуть, что функци она льная зависимость между величинами X
i
и
α
i
задана неявным образом. Чтобы найти X
1
, . . . , X
n
по заданным значениям
α
1
, . . . , α
n
, на до построить численное решение задачи Коши для системы (65)
порядка 2n, причем на каждом шаге численного интегрирования определять
управления u
1
(t), . . . , u
m
(t) из условий максимума фу нк ции Гамильтона, т.е.
из решения некоторой вспомогательной задачи нелинейного программирования.
Slide 66
'
&
$
%
Простейшие способы решения краевых задач (VI)
Редукция задачи расчета оптимальных программ к задаче
отыскания корней трансцендентной функции – 6
Редукция задачи определения оптимальной программы к задаче отыскания нулей
некоторой системы функций при другом задании краевых условий для системы
(65) проводится совершенно аналогично.
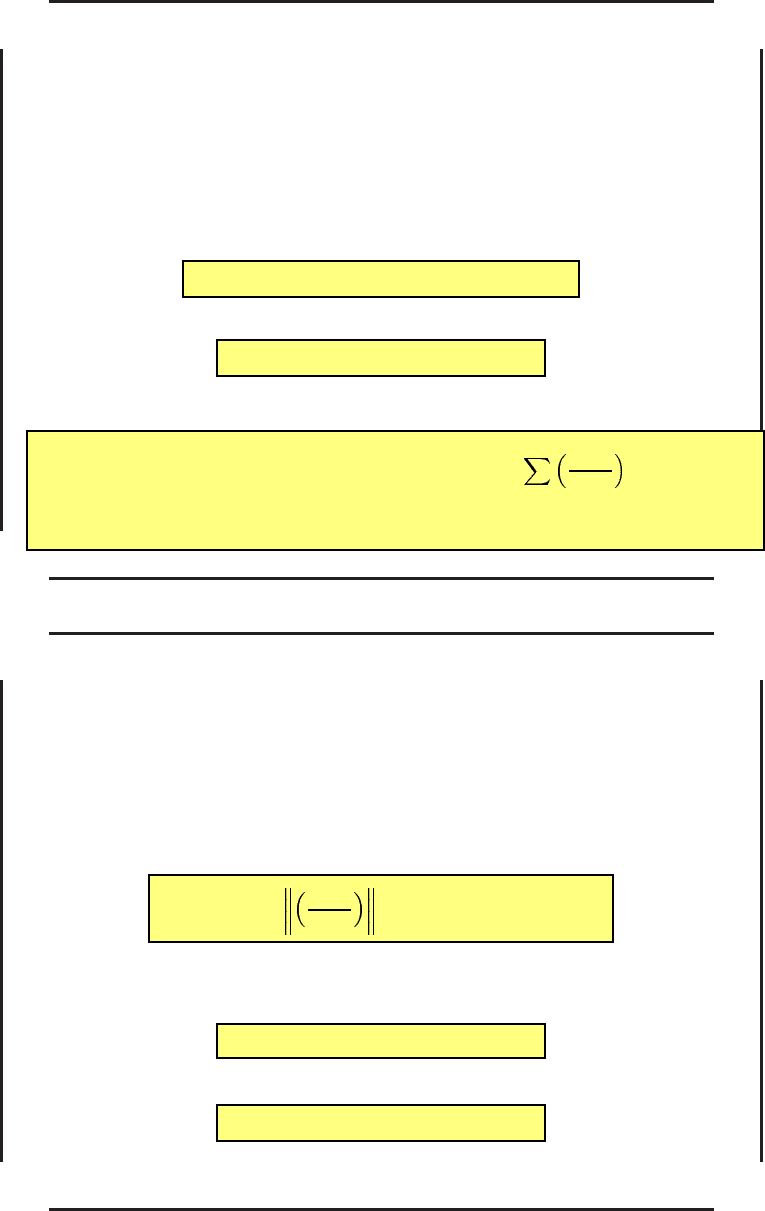
Система невязок ( 6 7) в случае, когда на концах заданы не все коо рдинаты,
дополняется соотношениями, получающимися из условий т рансверсальности
после исключения произвольных постоянных.
Ю. В. Тюменцев 33
Оптимальное управление
Slide 67
'
&
$
%
Простейшие способы решения краевых задач (VII)
Метод Ньютона для отыскания корней функции – 1
Задача отыскания корней функций — много разнообразных методов.
Один из самых старых методов такого рода — метод Ньютона, широко
используемый для решения прикладных задач.
Пусть имеется некоторое нулевое приближение — набор чисел {α
0j
}, которой
соответствуют величины
X
0
i
= X
i
(α
01
, α
02
, . . . , α
0n
).
Положим
α
1j
= α
0j
+ δ
1j
.
Считая величины δ
1j
малыми, примем
X
1
i
≡ X
i
(α
01
+ δ
11
, . . . , α
0n
+ δ
1n
) = X
0
i
+
n
j=1
∂X
i
∂α
j
α=α
0
δ
1j
,
i = 1, 2 , . . . , n.
Slide 68
'
&
$
%
Простейшие способы решения краевых задач ( VIII)
Метод Ньютона для отыскания корней функции – 2
Выберем теперь величины δ
1j
так, чтобы правые части этих ра венств обратились
в нуль. Это дает нам n линейных уравнений относительно n величин
δ
11
, . . . , δ
1n
. Введем матрицу A(α):
A(α) =
∂X
i
∂α
j
, i, j = 1, . . . , n.
Будем обозначать A(α
k
) через A
k
. Тогда уравнение относительно вектора
δ
1
= δ
11
, . . . , δ
1n
запишется в виде
A
0
δ
1
= −X
0
,
или
δ
1
= −A
−1
0
X
0
. (68)
Ю. В. Тюменцев 34
Оптимальное управление
Slide 69
'
&
$
%
Простейшие способы решения краевых задач ( IX)
Метод Ньютона для отыскания корней функции – 3
Примем теперь вектор α
0
+ δ
1
= α
1
и повторим процесс.
Общая схема итераций имеет следующий вид:
δ
k
= −A
−1
k−1
X
k−1
, α
k
= α
k−1
+ δ
k
. (69)
На каждой и терации н ужно вычислять матрицу A, причем производные придется
находить численно.
Это требует решения n + 1 задач Коши для системы (65) , порядок которой равен
2n.
Slide 70
'
&
$
%
Простейшие способы решения краевых задач ( X)
Метод Ньютона для отыскания корней функции – 4
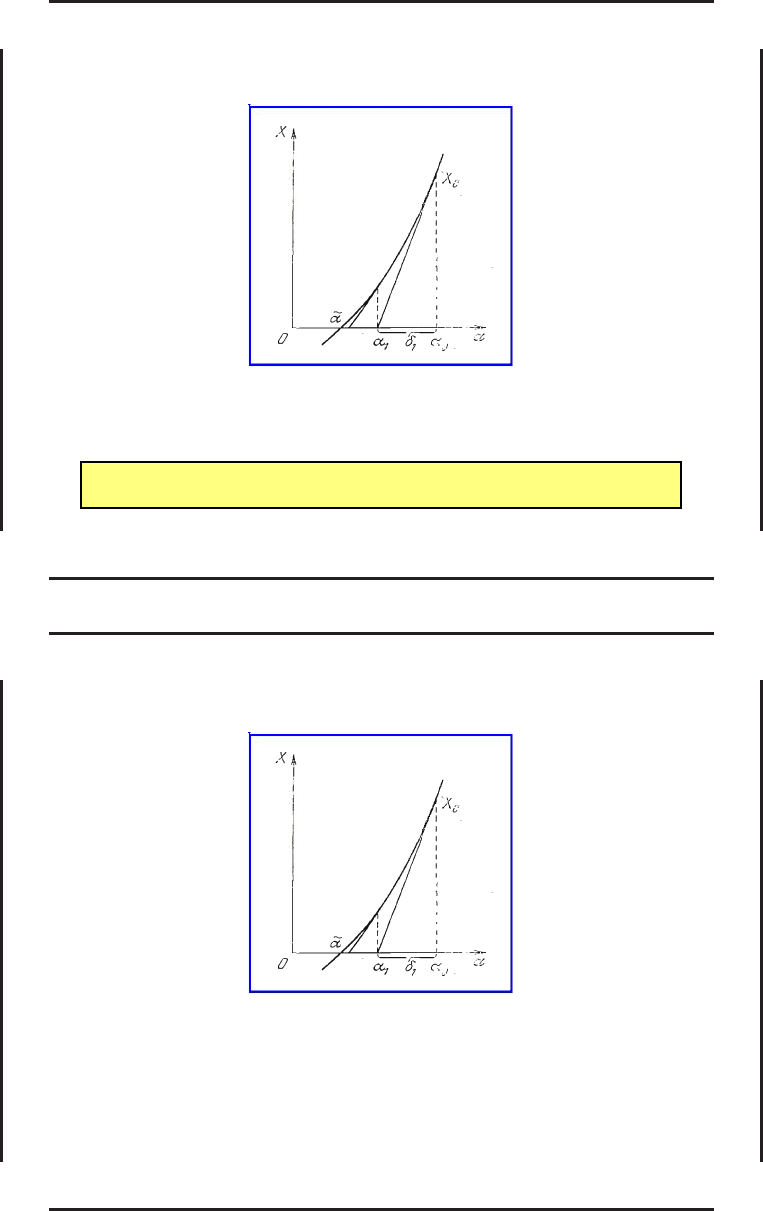
Метод Ньютона иногда называют мет одом касательных, основываясь на
следующей его ин терпретации. Пусть X и α — скаляры, требуется отыскать
корень функции одной переменной X(α).
В точке (α
0
, X
0
) проведем касательную к кривой X(α) (см. рис.), уравнение
которой имеет вид:
z(α) = X(α
0
) + X
′
(α
0
)(α − α
0
).
Ю. В. Тюменцев 35
Оптимальное управление
Slide 71
'
&
$
%
Простейшие способы решения краевых задач ( XI)
Метод Ньютона для отыскания корней функции – 5
Точку пересечения прямой z(α) с осью абсцисс примем в качестве нового
приближения α
1
. Зна чение α
1
будет определяться формулой (69)
δ
k
= −A
−1
k−1
X
k−1
, α
k
= α
k−1
+ δ
k
,
где A
−1
0
= 1/X
′
(α).
Slide 72
'
&
$
%
Простейшие способы решения краевых задач ( XII)
Метод Ньютона для отыскания корней функции – 6
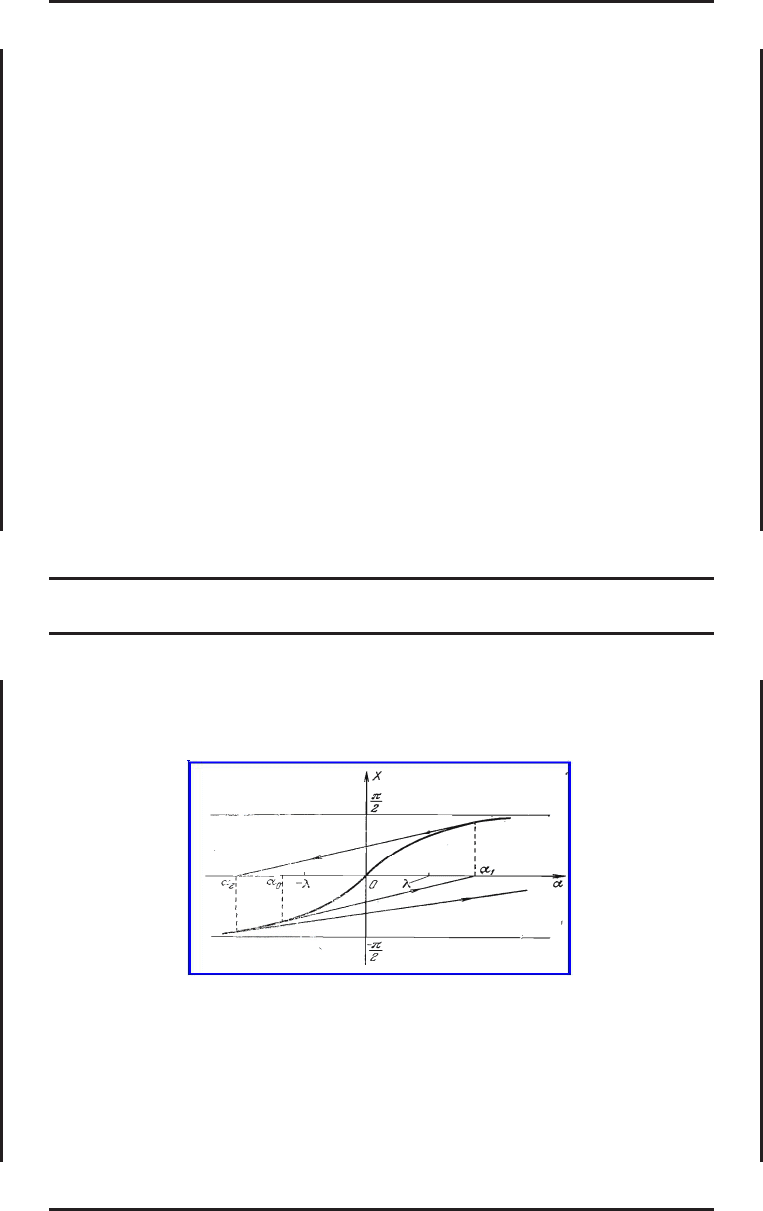
Таким образом, геометрически пр оцесс вычислений по методу Ньютона можно
представить следующим образом.
Задаем α
0
и вычисляем X
0
= X(α
0
), проводим в этой точке касательную и
точку ее пересечения с осью абсцисс принимаем в качестве нового значения
α = α
1
. Вычисляем затем X
1
= X(α
1
), проводим касательную и точку ее
пересечения с осью абсцисс принимаем в качестве α
2
и т.д.
Ю. В. Тюменцев 36
Оптимальное управление
Slide 73
'
&
$
%
Простейшие способы решения краевых задач ( XIII)
Сходимость метода Ньютона и его модификации – 1
Если нач альное приближение α
0
выбрано достаточно близко к значению корня
˜α, то метод Ньютона сходится очень быстро и удобен для практического
использования.
Однако если точка α
0
не находится в «области притяжения» корня, то метод
Ньютона расходится и не пригоден для практического использования.
Легко привести примеры, когда метод Ньютона приводит к расходящейся
последовательности итераций.
Slide 74
'
&
$
%
Простейшие способы решения краевых задач ( XIV)
Сходимость метода Ньютона и его модификации – 2
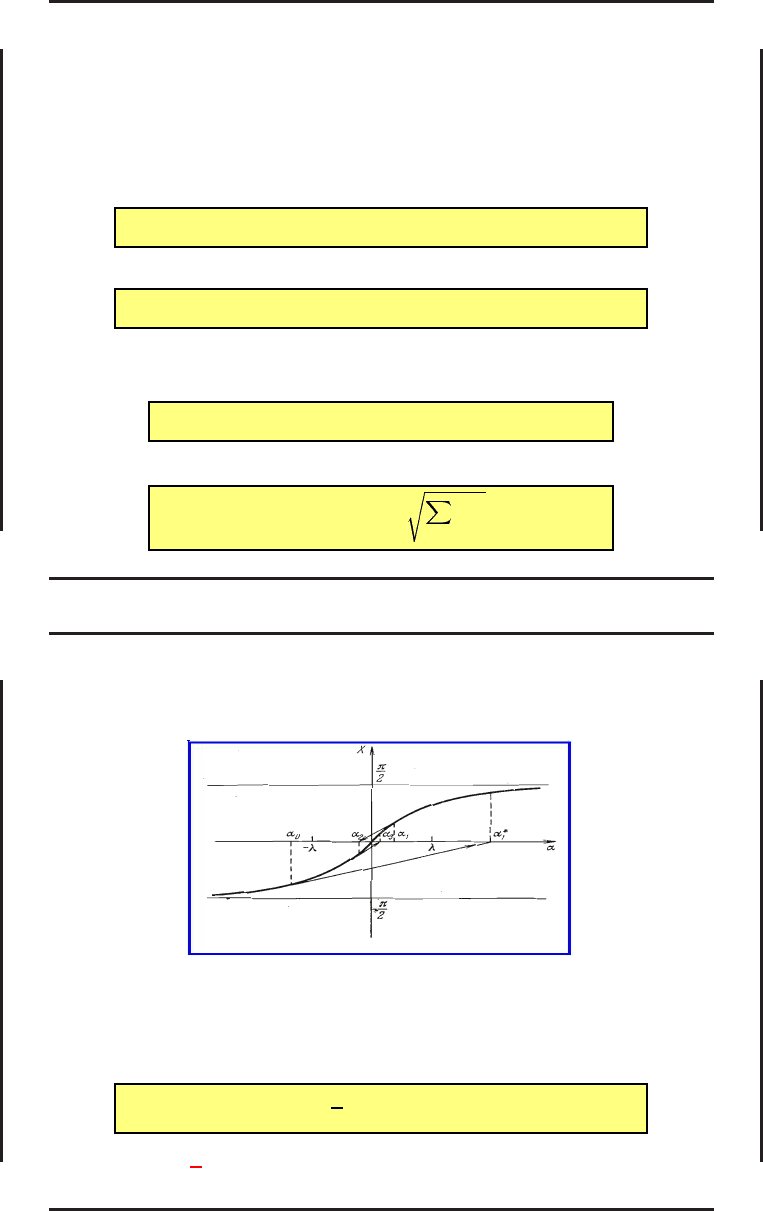
На рис. показан пример такого расходящегося процесса при поиске корня
функции X = arctg α.
Видно, что неудачный выбор начального приближения α
0
(оно было выбрано
как |α
0
| > λ, где λ — корень уравнения 2α = (1 + α
2
) arctg α), приводит к
тому, что каждое следующее значение переменной α отстоит все дальше и
дальше от значения корня.
Ю. В. Тюменцев 37
Оптимальное управление
Slide 75
'
&
$
%
Простейшие способы решения краевых задач (XV)
Сходимость метода Ньютона и его модификации – 3
Было предложено много модификаций метода Ньютона, в котор ых тем или иным способом
устраняется расходимость.
Одна из таких модификаций, довольно широко используем ая, состоит в том, что
первоначальная итерационная схема ( 69)
α
n+1
= α
n
− A
−1
(α
n
)X(α
n
)
заменяется следующей схемой:
α
n+1
= α
n
− κ
n
A
−1
(α
n
)X(α
n
),
где κ
n
— не который скалярный множитель, не превосходящий 1.
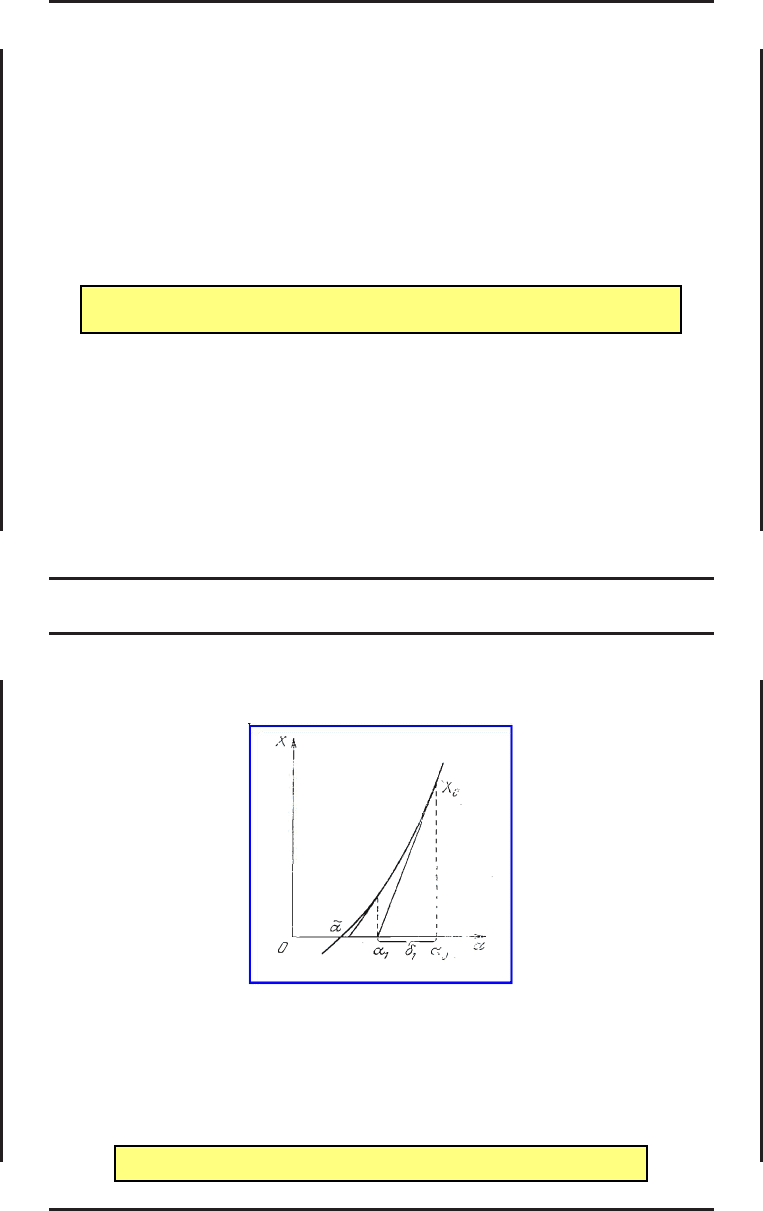
Существуют различные рецепты выбора этого множителя, но все они исходят из требования
||X(α
n+1
)|| < ||X(α
n
)||.
В качестве нормы ||X|| принимают обычно
max
i
|X
i
| или
i
X
2
i
.
Slide 76
'
&
$
%
Простейшие способы решения краевых задач ( XVI)
Сходимость метода Ньютона и его модификации – 4
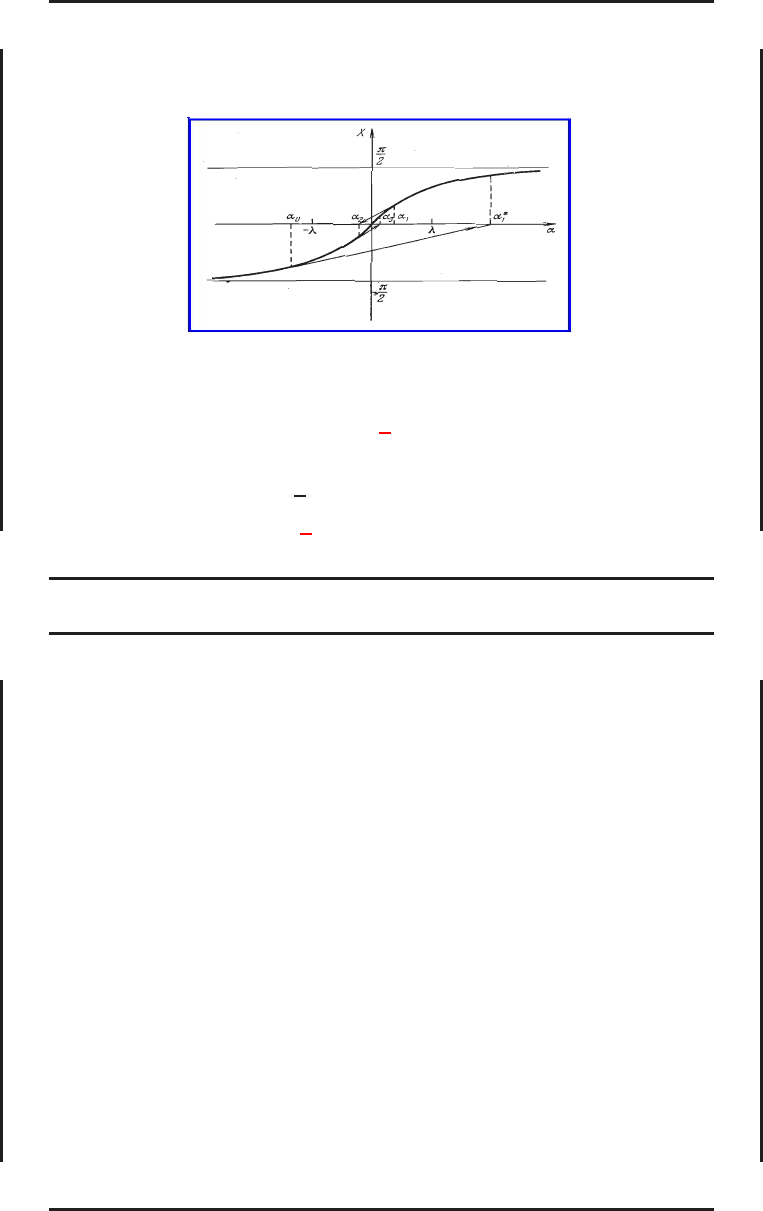
На этом рисунке изображена та ж е самая кривая, что и на предыдущем рисунке.
Обозначим через α
∗
1
значение α, полученное по схеме простого метода Ньютона, т.е. (69),
в котором κ
0
= 1. Как видно из рисунка, | X(α
∗
1
)| > |X(α
0
)|. Поэтому в качестве
нового приближения α выберем значение
α
1
= α
0
+
1
2
δ
1
, δ
1
= −A
−1
0
X
0
,
т.е. положим κ
0
=
1
2
.
Ю. В. Тюменцев 38
Оптимальное управление
Slide 77
'
&
$
%
Простейшие способы решения краевых задач (XVII)
Сходимость метода Ньютона и его модификации – 5
Видно, что α
1
находится уже в окрестности корня, где сходится простой метод Ньютона
(κ
n
= 1, n = 1, 2, . . .).
Итак, предложенный выбор множителя κ
0
=
1
2
, n = 1, 2, . . . сделал расходящийся
процесс сходящимся.
Если бы оказалось, что при κ
0
=
1
2
процесс все равно расходится, делается следующий
шаг, в котором принимается κ
0
=
1
4
, n = 1, 2, . . . и т.д.
Slide 78
'
&
$
%
Простейшие способы решения краевых задач
(XVIII)
Сходимость метода Ньютона и его модификации – 6
Несмотря н и на какие модификации, применение метода Ньютона невозможно без
удовлетворительного первого приближения.
Успех решени я задач при использовани и этого метода определяется, в пе рвую очередь,
удачным первым приближением.
Вопрос о первом приближении достаточно труден, поскольку надо подобрать начальные
значения импульсов, для которых в обще м случае нет хорошей динамической интерпретации.
Первый недостаток подхода, связанного с редукцией вариационной задачи к краевой и ее
последующим сведением к задаче отыскания нулей трансцендентной функции, заключается
именно в необходимости предварительного выбора первого приближения.
Второй недостаток этого подхода связан с возможной неустойчивостью процесса получения
требуемого решения.
В силу этих причин мет од Ньютона, несмотря на простоту и удобство использования, не стал
универсальным средством расчета оптимальных программ для того класса задач, к которым
можно применить принцип максимума Понтрягина.
Ю. В. Тюменцев 39

Оптимальное управление
Slide 79
'
&
$
%
Решение краевых задач — перенос граничных
условий (I)
Предварительные замечания
Методы, рассмотренные ранее, приводили к следующей схеме р асчета: задавая
тем или иным способом недостающие данные в задачу Коши для П-системы
(этим термином часто называют систему 2n уравнений, полученную в результате
применения принципа максимума Понтрягина), мы отыскивали точное решение
этой системы.
Полученные конечные значения не удовлетворяли краевым условиям.
Информация о величинах невязок позволяла определить новые значения
недостающих начальных условий и т.д.
К рассматриваемой проблеме можно подойти с других позиций, а именно,
отыскивать решение среди множества тех функций, которые удовлетворяют
краевым условиям.
Такие решения можно находить методами, основанными на переносе граничных
условий – методами прогонки.
Slide 80
'
&
$
%
Решение краевых задач — перенос граничных
условий (II)
Линейные задачи с квадратичным функционалом – 1
Рассмотрим управляемую систему, дв ижение которой описывается системой
дифференциальной урав нений вида:
˙x = Ax + Bu, (70)
где A и B — матрицы, элем енты которых — некоторые заданные ф ункции времени.
В скалярном виде система (70) запишется в виде:
˙x
i
=
n
j=1
a
ij
x
j
+
m
j=1
b
ij
u
j
. (71)
На управление u никаких ограничений не накладыв ается.
Пусть начальное состояние системы (70) фиксировано:
x(0) = x
0
. (72)
Ю. В. Тюменцев 40
