Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 1

Московский авиационный институт (МАИ)

Факультет авиационной техники

Кафедра динамики и управления

летательных аппаратов

Оптимальное управление

Ю.В.Тюменцев

Февраль–декабрь 2009 года

Slide 2

Оптимальное управление динамическими

системами — общие положения (I)

Виды задач оптимального упра в ления

Три класса задач:

1. Программирование оптимальных траекторий.

2. Синтез оптимального управления.

3. Оптимальное управление в конфликтной ситуа ц и и .

Задачи первого класса — формирование оптимального управления как функции

времени.

Задачи второго класса — формирование оптима льного управления как функц и и

фазовых координат системы.

Задачи третьего класса — вариационные задачи, которые содержат конфликт

(«преследование-уклонение»).

Ю. В. Тюменцев 1

Оптимальное управление

Slide 3

Оптимальное управление динамическими

системами — общие положения (II)

Формальное описание задачи оптимального у пра в ления – 1

Общая структура описания

Формальное описание для любой задачи оптимального управления содержит три

обязательных элемента:

❑ модель движения объекта управления;

❑ граничные условия;

❑ критерий оптимальности.

Slide 4

Оптимальное управление динамическими

системами — общие положения (III)

Формальное описание задачи оптимального управления – 2

Модель движения – 1

Модель движения объекта управления (ОУ) — система обыкновенных

дифференциальных уравнений в нормальной форме Коши, записанная в

векторном виде

˙x = X(x, u, t). (1)

или в координатном виде

˙x

= X

, . . . , x

, u

, . . . , u

, , t), k = 1, . . . , n. (2)

Здесь: x = (x

, . . . , x

) — вектор состояния ОУ;

X = (X

, . . . , X

) — вектор обобщенной силы, действующей на ОУ;

u = (u

, . . . , u

) — вектор управления;

t — время, определенное в интервале T = [t

, t

], если t < ∞, или же в

интервале T = [t

, t

), если t = ∞.

Все векторы принимают только вещественные значения.

Ю. В. Тюменцев 2

Оптимальное управление

Slide 5

Оптимальное управление динамическими

системами — общие положения (IV)

Формальное описание задачи оптимального управления – 3

Модель движения – 2

Область определения уравнений движения (1) или (2) — совокупность точек x,

u, для которых определены функции X

, k = 1, . . . , n. Обозначим ее через

N > 0:

(x, u, t) > 0, α = 1, . . . , s (3)

Это ограничения на состояния x и управления u рассматриваемого объекта.

Компоненты вектора x: величины, описывающие состояние объекта управления.

Это зависимые (связанные) величины, которые определяются уравнениями

движения (1).

Примеры

: скорость полета, высота полета, угловая скорость крена.

Компоненты вектора u: свободны для выбора в определенных пределах. Они

определяют характер движения ОУ.

Примеры

: углы отклонения рулей (высоты,

направления, элеронов и т.п.), перемещение рычага управления двигателем (РУД).

Slide 6

Оптимальное управление динамическими

системами — общие положения (V)

Формальное описание задачи оптимального у пра в ления – 4

Модель движения – 3

Управления являются допустимыми, если они получают значения из области

N > 0.

Управления обычно принадлежат классу непрерывных или

кусочно-непрерывн ых ограниченных функций.

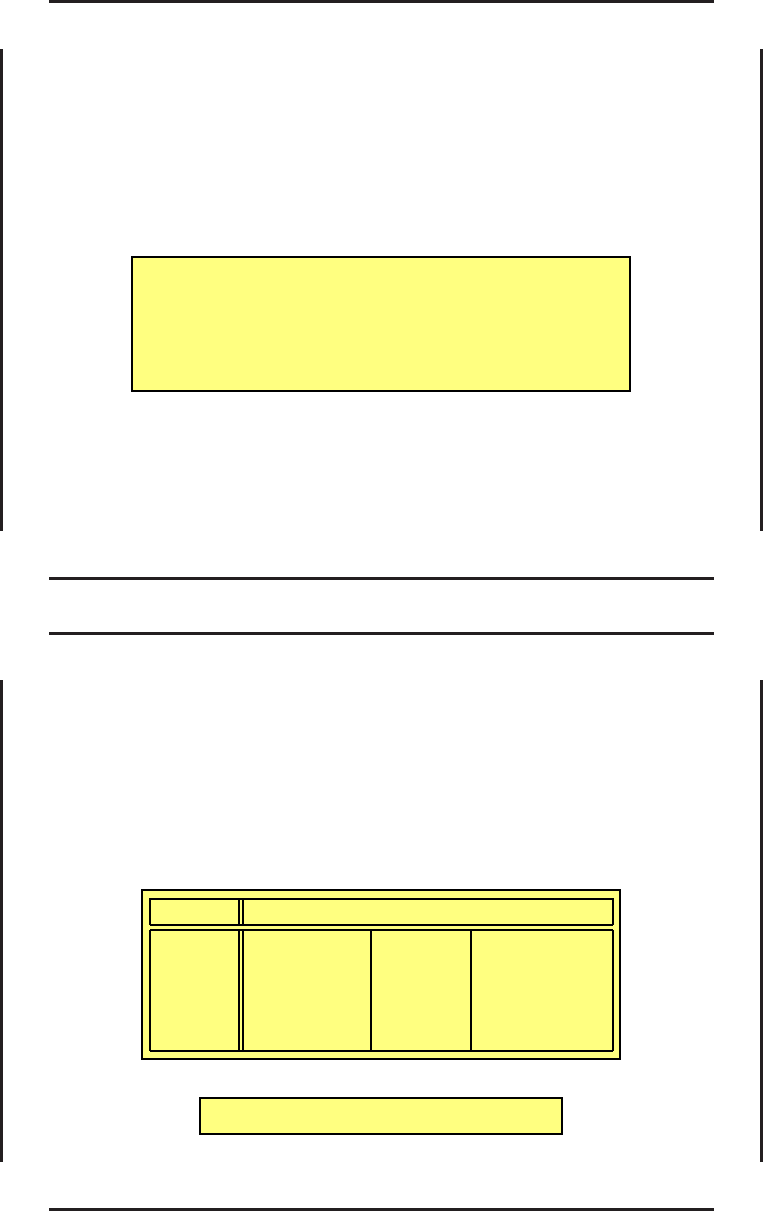
Уравнения движения (1) будут иметь решение

x = x[x(t

), u(t), t] (4)

при всяком u ∈ U и при любом начальном значении x

∈ N.

Ю. В. Тюменцев 3

Оптимальное управление

Slide 7

Оптимальное управление динамическими

системами — общие положения (VI)

Формальное описание задачи оптимального управления – 5

Модель движения – 4

Итак, задана математическая модель движения объекта управления, если:

1) заданы уравнения движения (1);

2) указана область определения N > 0 для них;

3) указан интервал T изменения времени t;

4) указан класс допустимых управлений U.

Функции X

в уравнениях движения (1) являются гладкими по всем аргументам

x, u, t в каждой точке области N > 0 и при всех t ∈ T .

Примеры: Уравнения управляемого движения самолета в течение заданного

промежутка времени, записываемые для различных случаев: продольное,

боковое, полное движение.

Slide 8

Оптимальное управление динамическими

системами — общие положения (VII)

Формальное описание задачи оптимального управления – 6

Граничные условия

Граничные условия — это условия, которым подчиняются значения состояний объекта

управления (его фазовых координат) x при t = t

и t = t

Различают три основных вида граничных условий:

t Концы траекторий изображающей точки

При t

фиксированы свободны лежат на

многообразиях

(x, t) = 0

При t

фиксированы свободны лежат на

многообразиях

(x, t) = 0

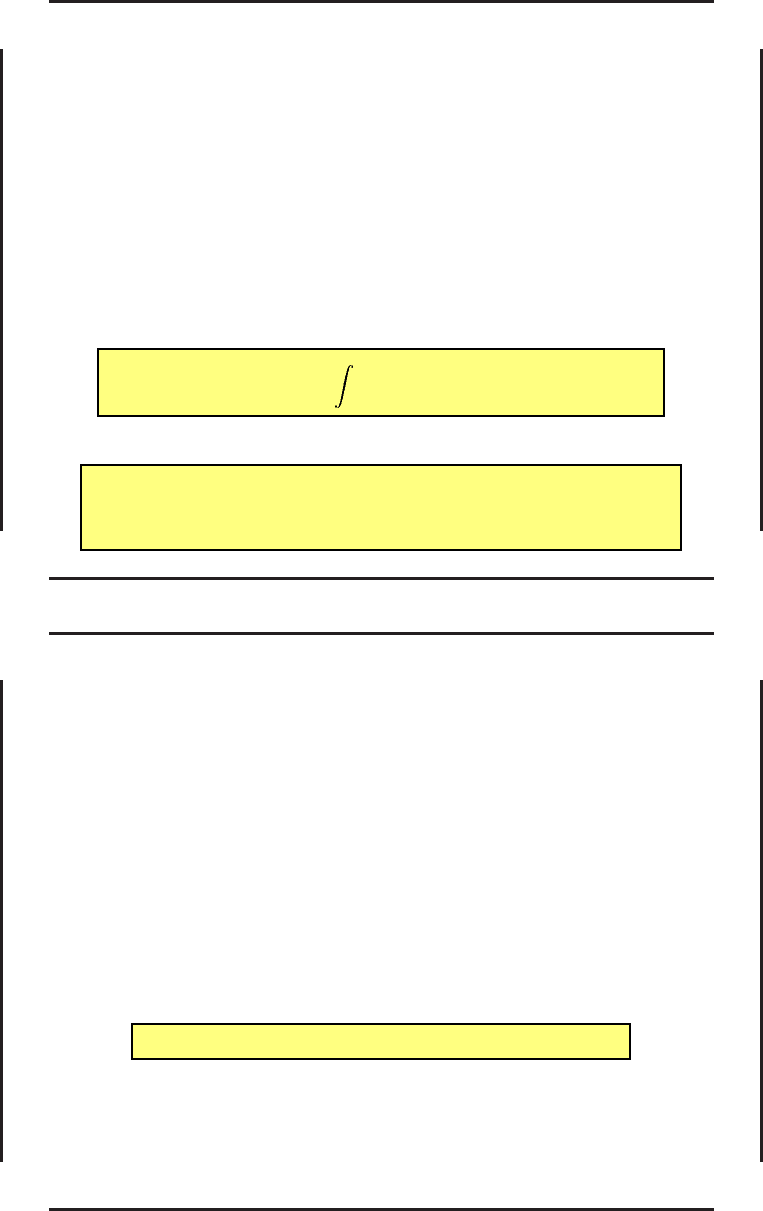
Символическая форма записи гр аничных условий задачи оптима льного управления:

(i, f ) = 0 (5)

Будем применять ее независимо от того, являются ли величины t

, t

фиксированными или

свободными для выбора.

Ю. В. Тюменцев 4

Оптимальное управление

Slide 9

Оптимальное управление динамическими

системами — общие положения (VIII)

Формальное описание задачи оптимального управления – 7

Критерий оптимальности – 1

Критерий оптимальности в виде оптимизирующего функционала — важнейший

элемент задачи оптимального управления.

Цель задачи оп т имального управления — определить управление u

, при

котором «плата за достижение цели» минимальна.

Функционал — это переменная величина I(y), численное значение которой

зависит от выбора одной или нескольких функций.

Пример функционала — интеграл вида:

I(y) =

F (x, y, ˙y)dx. (6)

Говорят, что функционал I(y) задан, если:

❑ задан класc Y функций y(x), x ∈ [a, b];

❑ указан закон, согласно которому каждому y(x) ∈ Y одно-

значно соответствует число I(y), I(y) < ∞.

Slide 10

Оптимальное управление динамическими

системами — общие положения (IX)

Формальное описание задачи оптимального управления– 8

Критерий оптимальности – 2

Перебирая кривые y ∈ Y , можно обнаружить минимальные или максим альные

(экстремальные) значения функционала I(y).

Будем говорить, что функционал I(y) достигает минимума на кривой y

(x),

если выполняется неравенство

I(y

) 6 I(y), ∀y ∈ Y. (7)

Кривая y

(x) называется экстремалью (и ли, в данном случае, минималью)

функционала I(y).

Ю. В. Тюменцев 5

Оптимальное управление

Slide 11

Оптимальное управление динамическими

системами — общие положения (X)

Задачи программирования оптимальных траекторий

В задачах программирования оптимальных траекторий рассматривается

формирование оптимального управления как функции времени.

Формальное описание для любой задачи оптимального управления содержит три

обязательных элемента:

❑ модель движения объекта управления;

❑ граничные условия;

❑ критерий оптимальности.

Пример задачи программирования оптимальных траекторий — полет самолета

на максимальную дальность.

Slide 12

Задачи программирования оптимальных

траекторий (I)

Математическая формулировка задачи – 1

Определить вектор-функции x(t ∈ R

), u(t ∈ R

) при t ∈ [t

, T ],

доставляющие минимум (максимум) функционалу

J = J(x, u) (8)

при дифференциальных связях

˙x = f(x, u, t), (9)

ограничениях вдоль траектории

(x, u, t) ∈ G (10)

и краевых условиях

(x, t

) ∈ E

, (x, T ) ∈ E

. (11)

Ю. В. Тюменцев 6

Оптимальное управление

Slide 13

Задачи программирования оптимальных

траекторий (II)

Математическая формулировка задачи – 2

Функции f

в модели движения (9) непрерывны и дифференцируемы

по совокупности переменных x и u.

Множество G (в ограничениях (10)) — некоторая область пространства

× R

Множества E

и E

(в краевых условиях (11)) — некоторые

многообразия в R

× R

Конкретизация выражений (8)–(11) порождает различные типы задач

оптимального управления.

Slide 14

Задачи программирования оптимальных

траекторий (III)

Типы задач оптимального программирования

Типы задач оптимального программирования для объекта управления (9)

можно разбить на группы, в каждой из которых определяющей

характеристикой являются способы, с помощью которых задаются:

1. Функционал (8).

2. Ограничения вдоль траектории (10).

3. Краевые условия (11).

Ю. В. Тюменцев 7

Оптимальное управление

Slide 15

Задачи программирования оптимальных

траекторий (IV)

Способы задания функционала

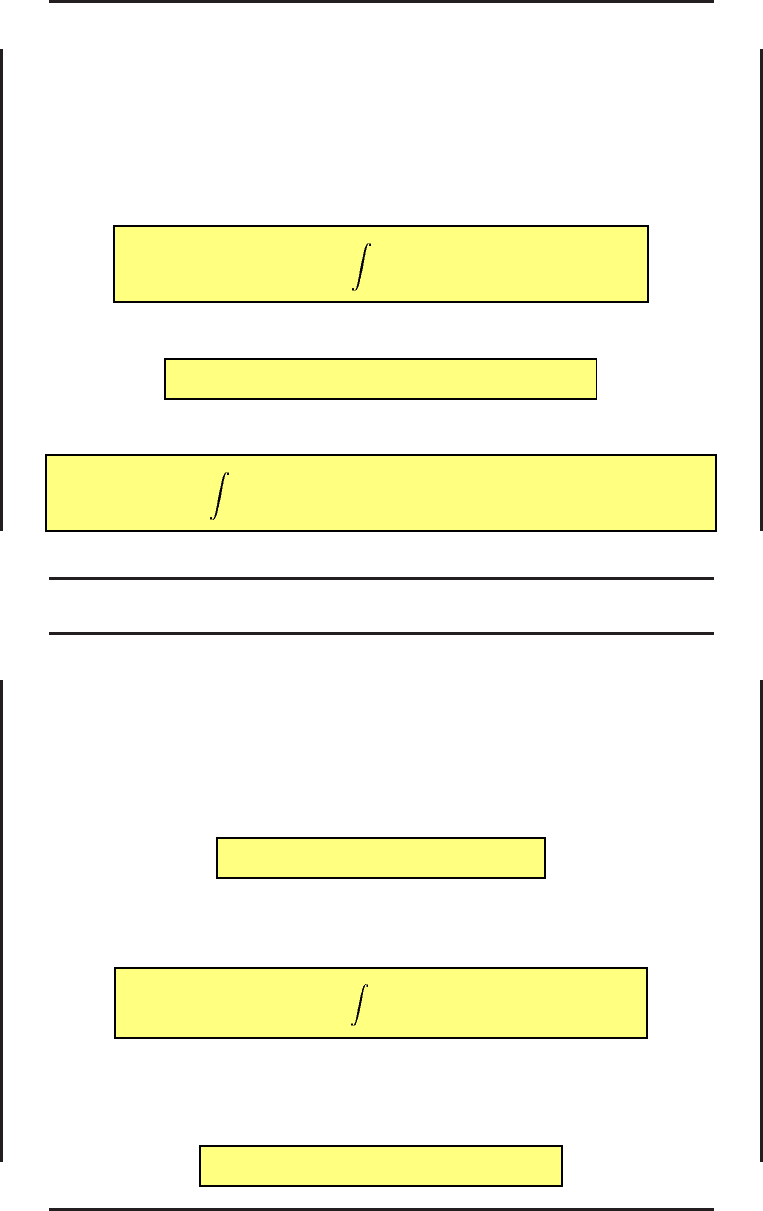
Задача Лагранжа

J(x, u) =

F (x, u, t)dt (12)

Задача Майера

J(x, u) = Φ(x(T ), T ) (13)

Задача Больца

J(x, u) =

F (x, u, t)dt + Φ(x(t

), t

, x(T ), T ) (14)

Slide 16

Задачи программирования оптимальных

траекторий (V)

Способы задания ограничений вдоль траектории – 1

Ограничения на управление

Ограничение (10) чаще всего имеет вид

u(t) ∈ G

(t), (15)

где G

— некоторое замкнутое множество из R

В частн ом случае, когда G

совпадает со всем пространством R

, а

функционал задан в виде

J(x, u) =

F (x, u, t)dt,

получаем обычную задачу Лагранжа.

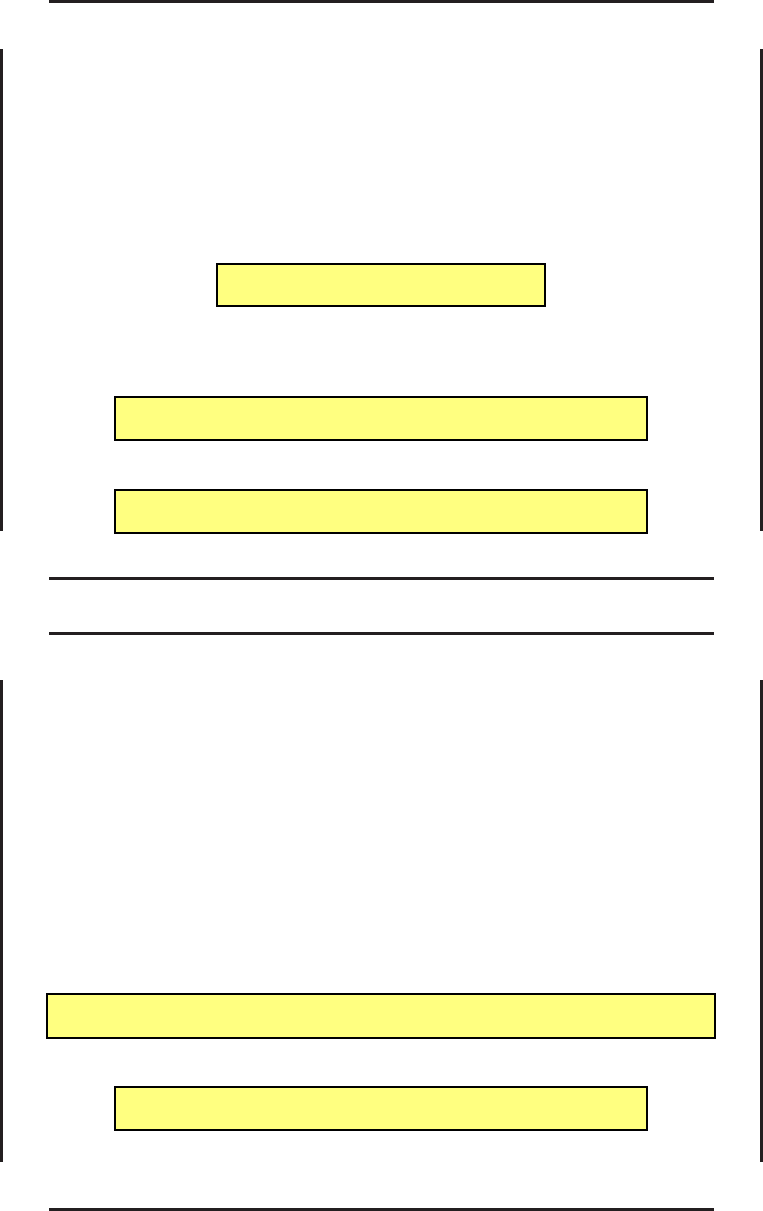
Задачи с ограничениями вида (15) типичны для техники — ресурсы, выделяемые

на управление, всегда ограничены. Например, часто встречаются ограничения

вида

|u(t)| 6 α(t). (16)

Ю. В. Тюменцев 8

Оптимальное управление

Slide 17

Задачи программирования оптимальных

траекторий (VI)

Способы задания ограничений вдоль траектории – 2

Ограничения на фазовы е переменны е

Это разновидность ограничений (10), чаще всего и меющая вид:

x(t) ∈ G

(t), (17)

где G

— некоторое замкнутое множество из R

Ограничения на фазовые координаты могут быть типа равенства

(x(t), t) = 0, j = 1, 2, . . . , k 6 n (18)

и типа неравенства

(x(t), t) 6 0, j = 1, 2 , . . . , p. (19)

Slide 18

Задачи программирования оптимальных

траекторий (VII)

Способы задания ограничений вдоль траектории – 3

Совместные ограничения на управ лен ия и фазовые переменные

В ряде случаев ограничения на управления и фазовые переменные не могут быть

разделены и их приходится учи тывать совместно.

Они могут быть как типа равенства

(x(t), u(t), t) = 0, j = 1, 2, . . . , k 6 n + m, (20)

так и типа неравенства

(x(t), u(t), t) 6 0, j = 1, 2 , . . . , k. (21)

Ю. В. Тюменцев 9

Оптимальное управление

Slide 19

Задачи программирования оптимальных

траекторий (VIII)

Способы задания ограничений вдоль траектории – 4

Интегральные ограничения – 1

Задача с интегральными ограничениями (изопериметрическая задача) —

определить минимум функционала

J(x, u) =

F (x, u, t)dt,

при следующих ограничениях:

(x(t), u(t), t)dt = L

, j = 1, 2, . . . , k, (22)

где Ψ

— некоторые скалярные функц и и , а L

— заданные числа.

Название этого класса задач — от задачи , решавшейся в XVII веке: определить

кривую данной длины, которая ограничивает максимальную площадь.

Slide 20

Задачи программирования оптимальных

траекторий (IX)

Способы задания ограничений вдоль траектории – 5

Интегральные ограничения – 2

Технический пример (изопе риметрической задачи) — расходование

имеющегося запаса топлива наилучшим образом (пролететь наибольшее

расстояние, пробыть в воздухе наибольшее время).

Изопериметрическая задача может быть сведена к задаче Лагранжа (или Майера,

в зависимости от структуры используемого функционала) увеличением

размерности фазового вектора x. Для этого достаточно ввести новые скалярные

переменные при помощи ура внений

˙x

n+j

= Ψ

(x, u, t), j = 1, 2, . . . , k,

Функции x

n+j

(t) должны при этом удовлетворять условиям

n+j

) = 0, x

n+j

(T) = L

Таким образом, изопериметрическая задача сводится к задаче Лагранжа (или

Майера), в которой вектор x получает размерность n + k вместо исходной

размерности n.

Ю. В. Тюменцев 10