Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 21

Задачи программирования оптимальных

траекторий (X)

Способы задания краевых условий – 1

(a) (b)

В общем случае многообразия E

и E

в (11) — это некоторые

гиперповерхности в пространстве (x, t), задаваемые уравнениями

: χ

(x(t

), t

) = 0, l = 0, 1, . . . , s 6 n, (23)

: Φ

(x(T ), T ) = 0, j = 0, 1, . . . , p 6 n. (24)

Slide 22

Задачи программирования оптимальных

траекторий (XI)

Способы задания краевых условий – 2

Задача с фиксир ованными концами. Здесь заданы x(t

) и x(T). Различают

также задачи с фиксированным временем (t

и T заданы) и нефиксированным

временем (либо t

, либ о T не задано).

Задача со свободным концом. Если x(t

) (или x(T )) не задано, то это задача

со свободным левым (правым) концом.

Задача с подвижными концами. Если t

, T — фиксированы, а x(t

) и x(T)

лежат на гиперповерхностях, определяемых уравнениями (23) и (24), то говорят о

задаче с подвижными концами и фиксированным временем. Если либ о t

, либо T

в (23), (24) не фи ксировано, то получаем задачу с «перемещающимися

многообразием» на соответствующем конце.

Ю. В. Тюменцев 11

Оптимальное управление

Slide 23

Необходимы е условия оптимальности в задачах

программирования траекторий (I)

Задачи классического вариационного исчисления – 1

Задача Лагранжа

Задача Лагранжа классического вариационного исчисления: определить

непрерывную вектор-функцию u(t ∈ R

) и дифференцируемую

вектор-функцию x(t ∈ R

), доставляющие ми нимум функционалу

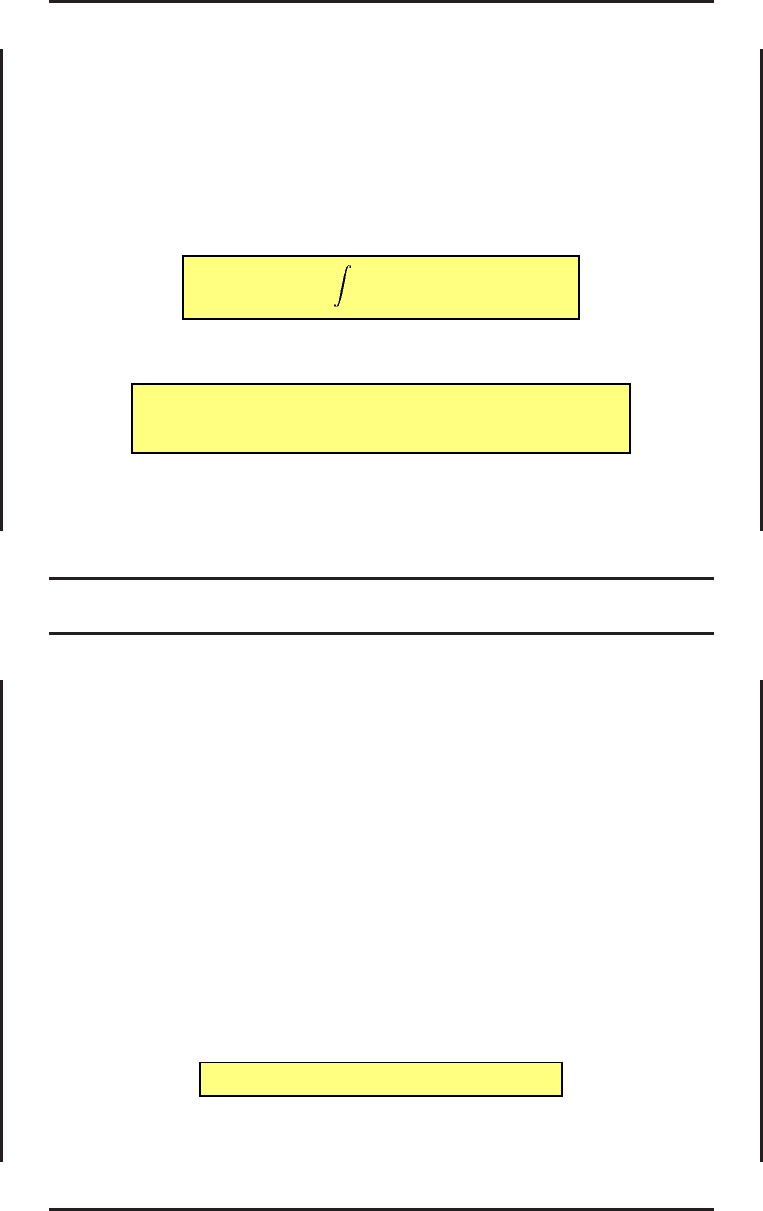
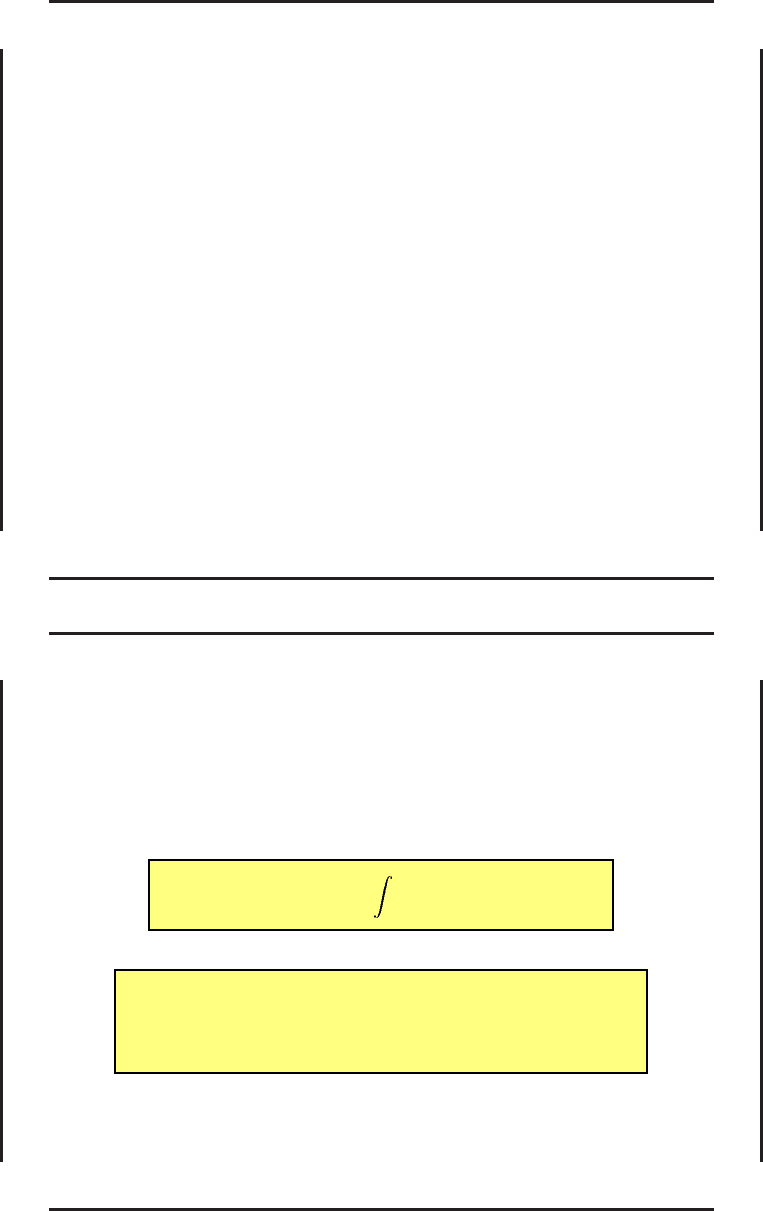
J(x, u) =

F (x, u, t)dt, (25)

где F — скалярная непрерывно-дифференцируемая функция своих аргументов,

при условиях

˙x = f(x, u, t), (26)

(x, t

) ∈ E

, (x, T ) ∈ E

, (27)

где f — непрерывно-дифференцируемая вектор-функция, E

и E

— заданные

множества из R

n+1

Замечание: методы, предлагаемые для з адачи Лагранжа, могут быть применены

также и для решения задач Майера и Больца.

Slide 24

Необходимы е условия оптимальности в задачах

программирования траекторий (II)

Задачи классического вариационного исчисления – 2

Вариации управления и траектории – 1

Пусть ˜u — некоторое управление, тогда соответствующая траектория ˜x

определяется как решение задачи Коши для уравнения (26).

Пусть также ε — некоторый скаляр (положительный или отрицательный),

а δu — произвольная непрер ывная функция.

Наряду с управлением ˜u рассмотрим управление u

= ˜u + εδu.

Вектор δu — вариация управления.

Ю. В. Тюменцев 12

Оптимальное управление

Slide 25

Необходимы е условия оптимальности в задачах

программирования траекторий (III)

Задачи классического вариационного исчисления – 3

Вариации управления и траектории – 2

Через x

обозначим траекторию, определенную управлением u

. Функция x

будет удовлетворять уравнению

˙x

= f(x

, ˜u + εδu

, t).

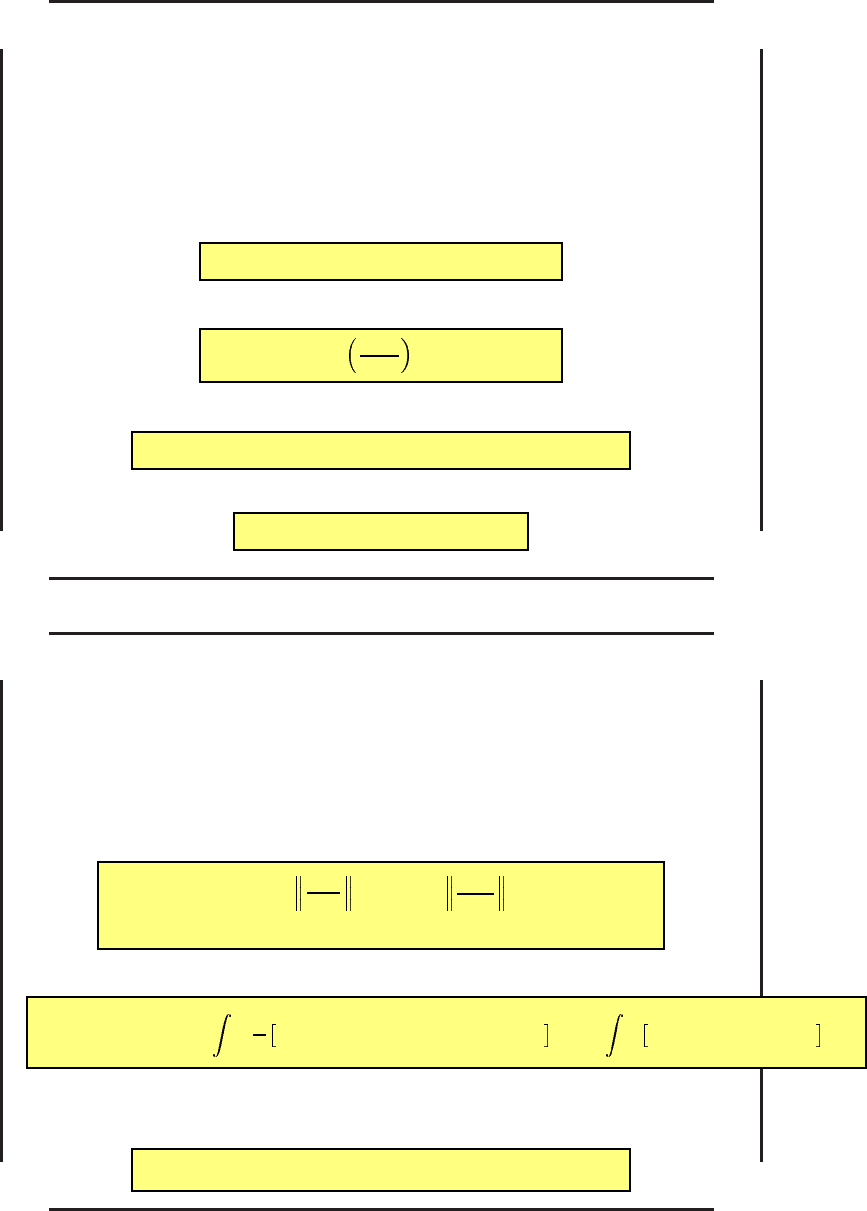
Вариацией фазовой траектории будем называть векторную производную

h =

∂x

∂ε

ε=0

Функция h(t) удовлетворяет уравнению

h = f

h + f

δu) (28)

с начальным условием

h(t

) = 0.

Slide 26

Необходимы е условия оптимальности в задачах

программирования траекторий (IV)

Задачи классического вариационного исчисления – 4

Вариации управления и траектории – 3

Уравнение (28) — это уравнение в вариациях. Здесь

∂f

∂x

, f

∂f

∂u

i = 1, 2 , . . . , n, j = 1, 2, . . . , n, k = 1, 2, . . . , m.

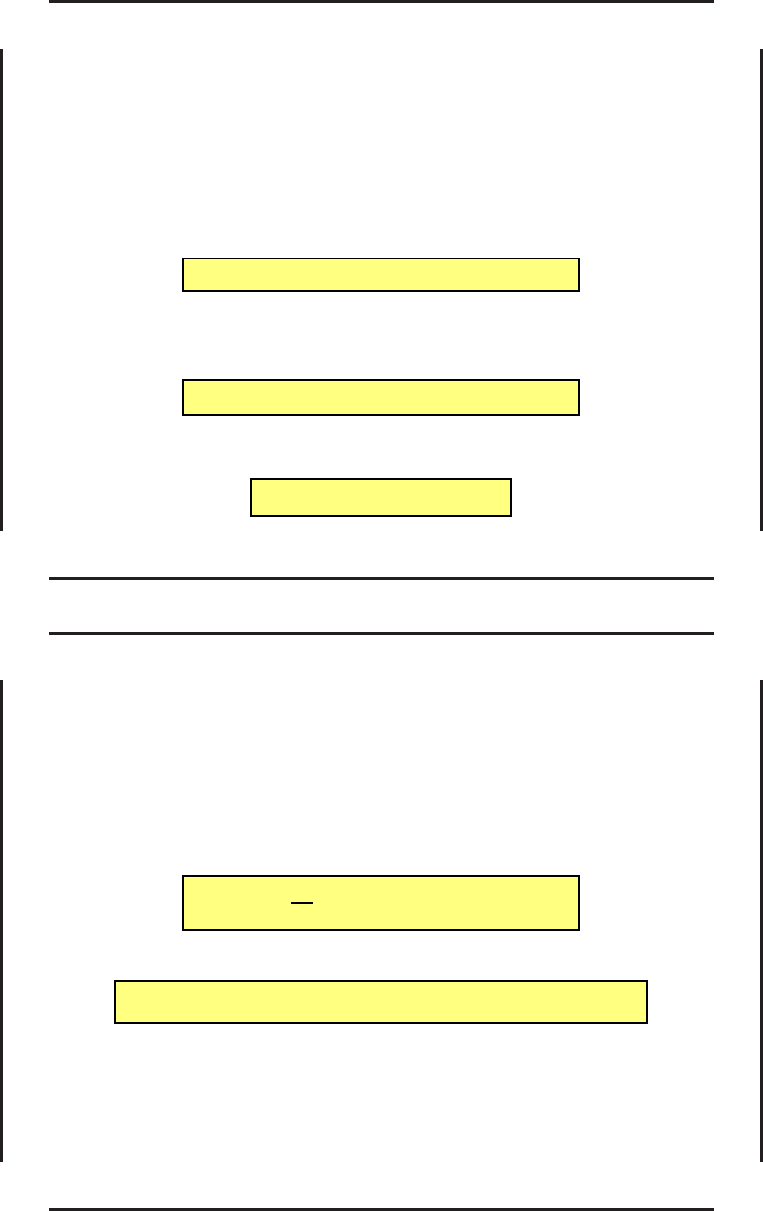
Вариацией функционала будем называть производную

δJ = ξ(T) = lim

ε→0

F (x

, ˜u+εδu, t)−F (˜x, ˜u, t) dt =

, h)+(F

, δu) dt,

где F

, F

— векторы частных производных F по x и u.

Функция ξ(t) удовлетворяет, очевидно, следующей задаче Коши:

ξ = (F

, h) + (F

, δu), ξ(0) = 0. (29)

Ю. В. Тюменцев 13

Оптимальное управление

Slide 27

Необходимы е условия оптимальности в задачах

программирования траекторий (V)

Задачи классического вариационного исчисления – 5

Сопряженные (двойственные) переменные – 1

Сопряженные (двойственные) переменные — возникают при введении

понятия сопряженной системы ура внений.

Пусть имеется линейное неоднородное уравнение

˙x = Ax + b, (30)

где A и b — матрица и вектор, элементы которых a

и b

— заданные функции

времени.

Системой, сопряженной (30), называется система вида

ψ = −A

∗

ψ, (31)

где A

∗

— сопряженная (транспонированная) матрица, элементы которой

получены перестановкой строк и столбцов матрицы A:

∗

= a

Вектор ψ, удовлетворяющий уравнению (31), называется вектором сопряженных

или двойственных переменных.

Slide 28

Необходимы е условия оптимальности в задачах

программирования траекторий (VI)

Задачи классического вариационного исчисления – 6

Сопряженные (двойственные) переменные – 2

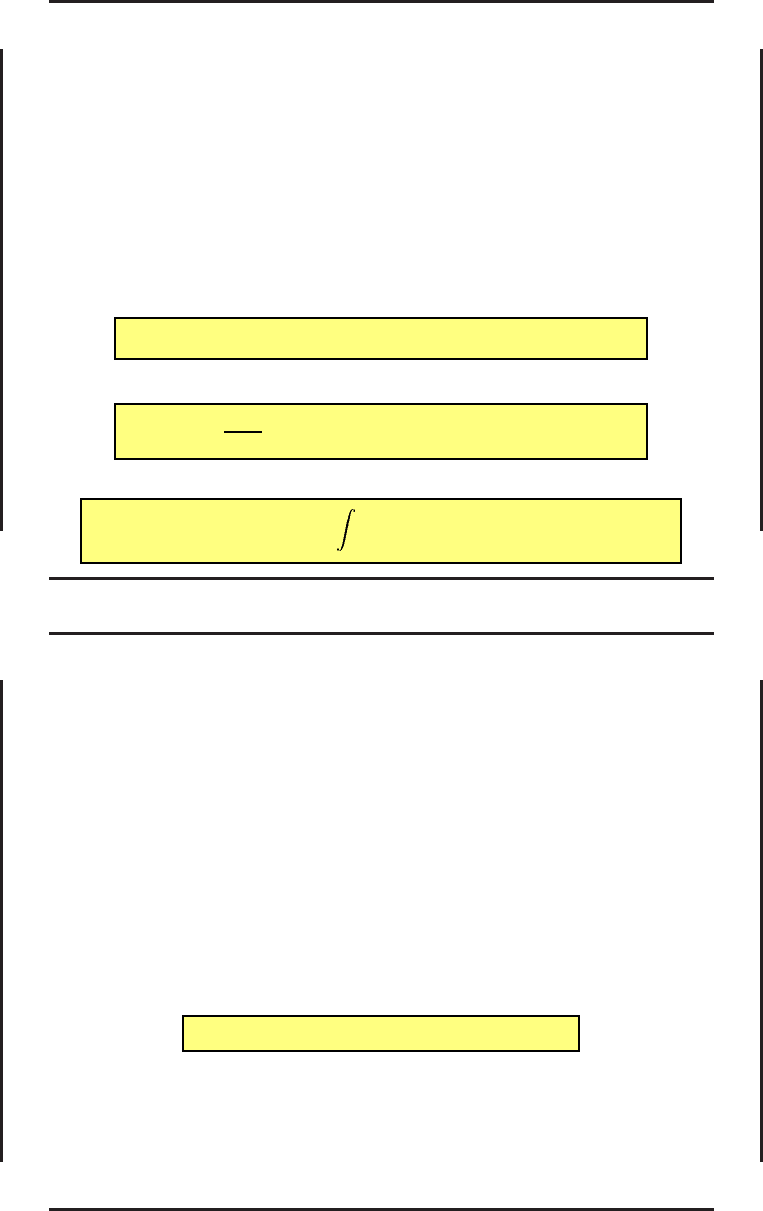
Векторы x и ψ обладают следующим важным свойством:

(ψ, x) = (ψ, b). (32)

Составим систему уравнений, сопряженную системе (28), (29):

ψ = −f

∗

ψ − F

, ψ

= 0, (33)

где ψ — n-мерный вектор, ψ

— скаляр.

Сопряженные переменные ψ

, ψ

, . . . , ψ

называются также множителям и

Лагранжа или импульсами.

В силу однородности, уравнения (33) определяют сопряженные переменные с

точностью до постоянного множителя.

Ю. В. Тюменцев 14

Оптимальное управление

Slide 29

Необходимы е условия оптимальности в задачах

программирования траекторий (VII)

Задачи классического вариационного исчисления – 7

Сопряженные (двойственные) переменные – 3

Используя сопряженные переменные, можно получить выражение для вариации

функционала в форме, удобной для составления необходимых условий

минимума.

Составим скалярное произведение

M(t) = ( ψ, h) + ψ

ξ. (34)

На основании свойства (32)

= (ψ, f

δu) + ψ

, δu), (35)

откуда

M(t) − M(t

) =

((ψf

+ ψ

), δu)dt. (36)

Slide 30

Необходимы е условия оптимальности в задачах

программирования траекторий (VIII)

Задачи классического вариационного исчисления – 8

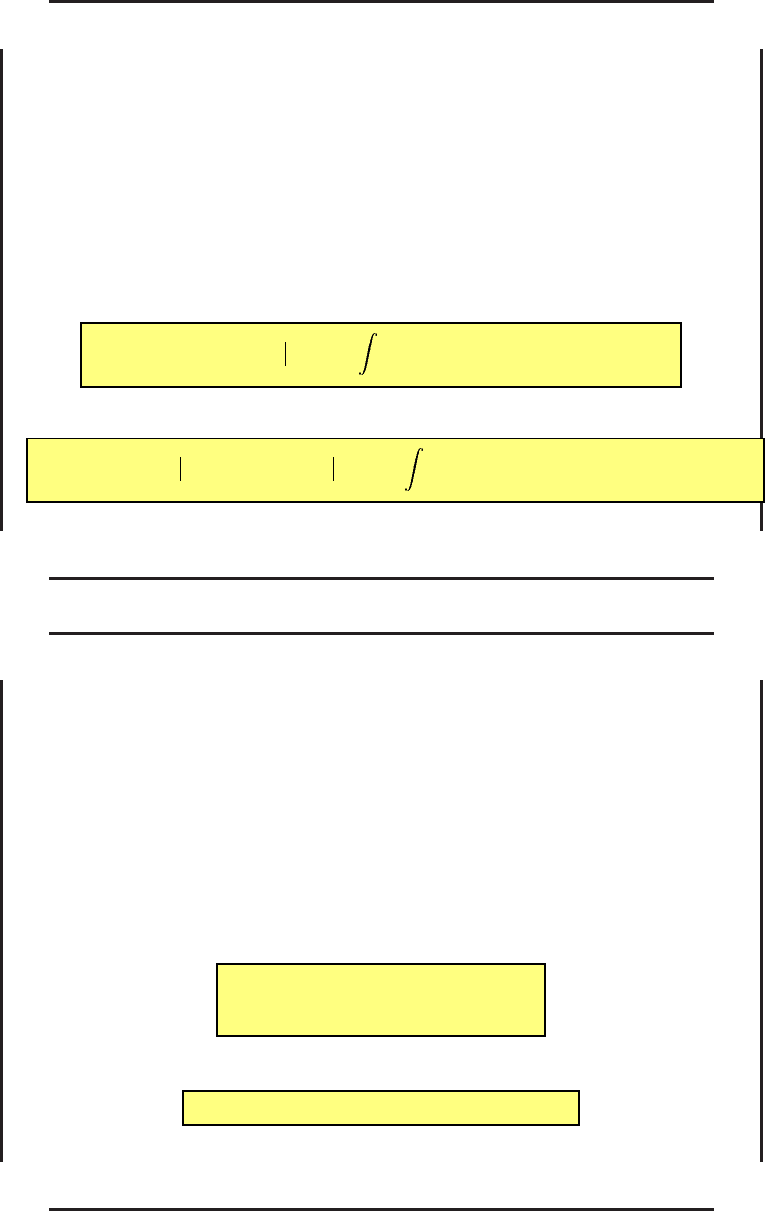
Необходимые условия минимума в задаче со свободным концом – 1

Необходимые условия минимума рассмотрим применительно к з адаче Лагранжа

со свободным правым концом.

Краевые условия такой задачи:

x(t

) = x

, t

, T заданы. (37)

На правый конец фазовой траектории x(T) никаких ограничений не

накладывается.

Ю. В. Тюменцев 15

Оптимальное управление

Slide 31

Необходимы е условия оптимальности в задачах

программирования траекторий (IX)

Задачи классического вариационного исчисления – 9

Необходимые условия минимума в задаче со свободным концом – 2

Из (34), согласно (28) и (29), при t = t

имеем M(t

) = 0, поэтому из (36)

получаем

((ψ, h) + ψ

ξ)

t=T

((ψf

+ ψ

), δu)dt,

откуда

(ψ

ξ)

t=T

= −(ψ, h)

t=T

((ψf

+ ψ

), δu)dt. (38)

Slide 32

Необходимы е условия оптимальности в задачах

программирования траекторий (X)

Задачи классического вариационного исчисления – 10

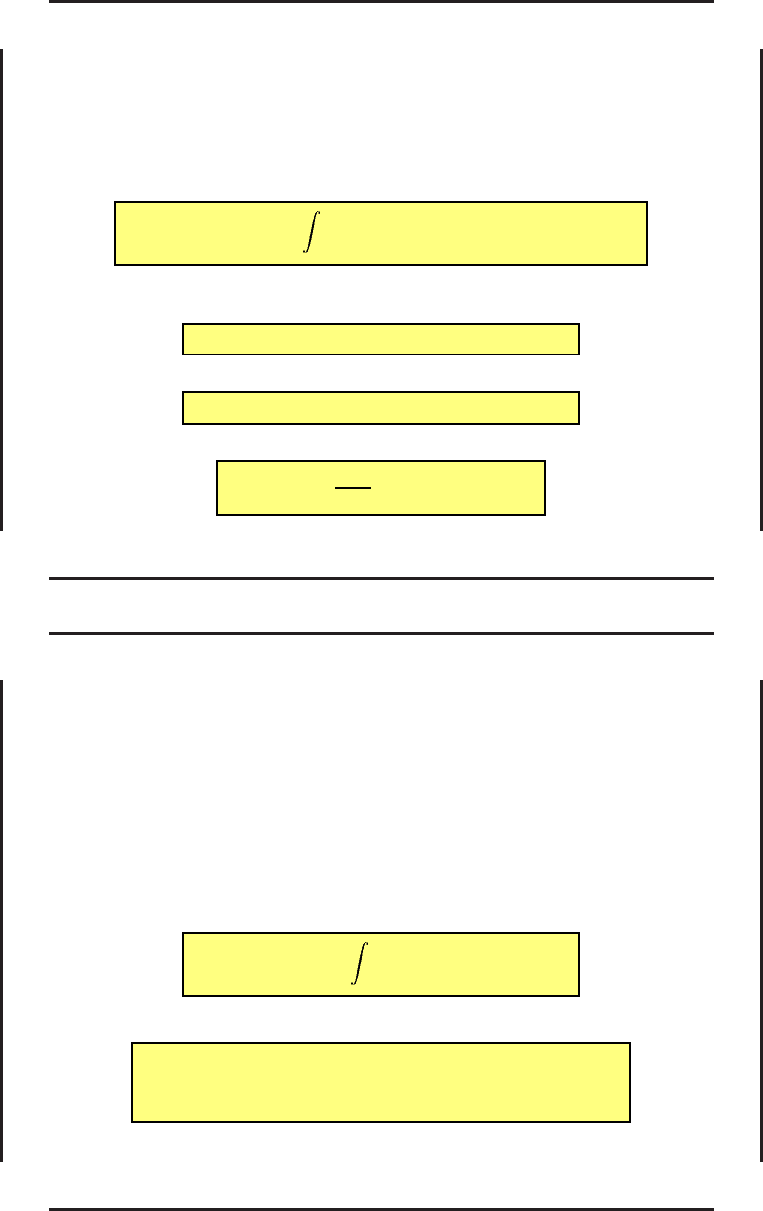
Необходимые условия минимума в задаче со свободным концом – 3

Распорядимся вектор ом сопряженных переменных, подчинив значения ψ

(T )

и ψ(T) следующим условиям:

ψ(T) = 0, (39)

(T) = −1. (40)

Так как ψ

= 0, то для любого t

= const = −1.

Ю. В. Тюменцев 16

Оптимальное управление

Slide 33

Необходимы е условия оптимальности в задачах

программирования траекторий (XI)

Задачи классического вариационного исчисления – 11

Необходимые условия минимума в задаче со свободным концом – 4

Для вариации функционала получаем следующее выражение:

δJ = −

((ψf

− F

), δu)dt. (41)

Пусть ˜u(t) — оптим ально е управление. Тогда δJ = 0 для любых δu, не

стесненных никакими условиями. Отсюда следует, что для любого t

ψf

− F

= 0. (42)

Если ввести функцию Гамильтона

H = (ψf) − F, (43)

то условие (42) можно записать в виде

∂H

∂u

= 0. (44)

Итак, получены необходимые условия оптимальности, которые можно

сформулировать в виде следующей теоремы.

Slide 34

Необходимы е условия оптимальности в задачах

программирования траекторий (XII)

Задачи классического вариационного исчисления – 12

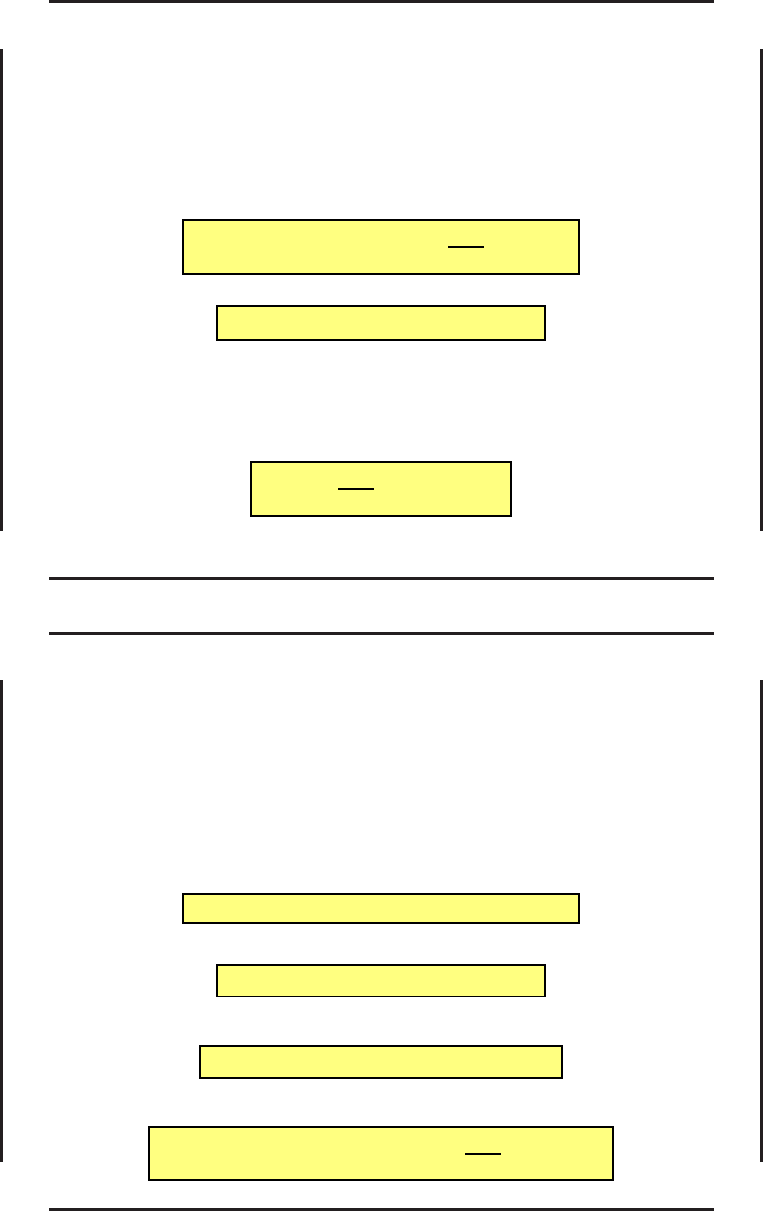
Необходимые условия минимума в за д аче со свободным концом – 5

Теорема. Если функ ц и и ˜u(t) и ˜x(t) доставляют м и нимум функционалу (25)

J(x, u) =

F (x, u, t)dt,

при условиях (26), (37)

˙x = f(x, u, t),

x(t

) = x

, t

, T заданы,

Ю. В. Тюменцев 17

Оптимальное управление

Slide 35

Необходимы е условия оптимальности в задачах

программирования траекторий (XIII)

Задачи классического вариационного исчисления – 13

Необходимые условия минимума в задаче со свободным концом – 6

то существует такая непрерывная вектор-функция ψ(t), удовлетворяющая

уравнению

ψ = −f

∗

ψ + F

= −

∂H

∂x

(45)

и условию

ψ(T) = 0, (46)

то управление ˜u(t) в каждый момент времени t является стационарной точкой

функции Гамильтона.

Условие (46) представляет собой частный случай условий т рансверсальности.

Сопряженные уравнения (45) и условия стационарности (44)

∂H

∂u

= 0

представляют собой уравнения Эйлера кл ассического вариационного

исчисления.

Slide 36

Необходимы е условия оптимальности в задачах

программирования траекторий (XIV)

Задачи классического вариационного исчисления – 14

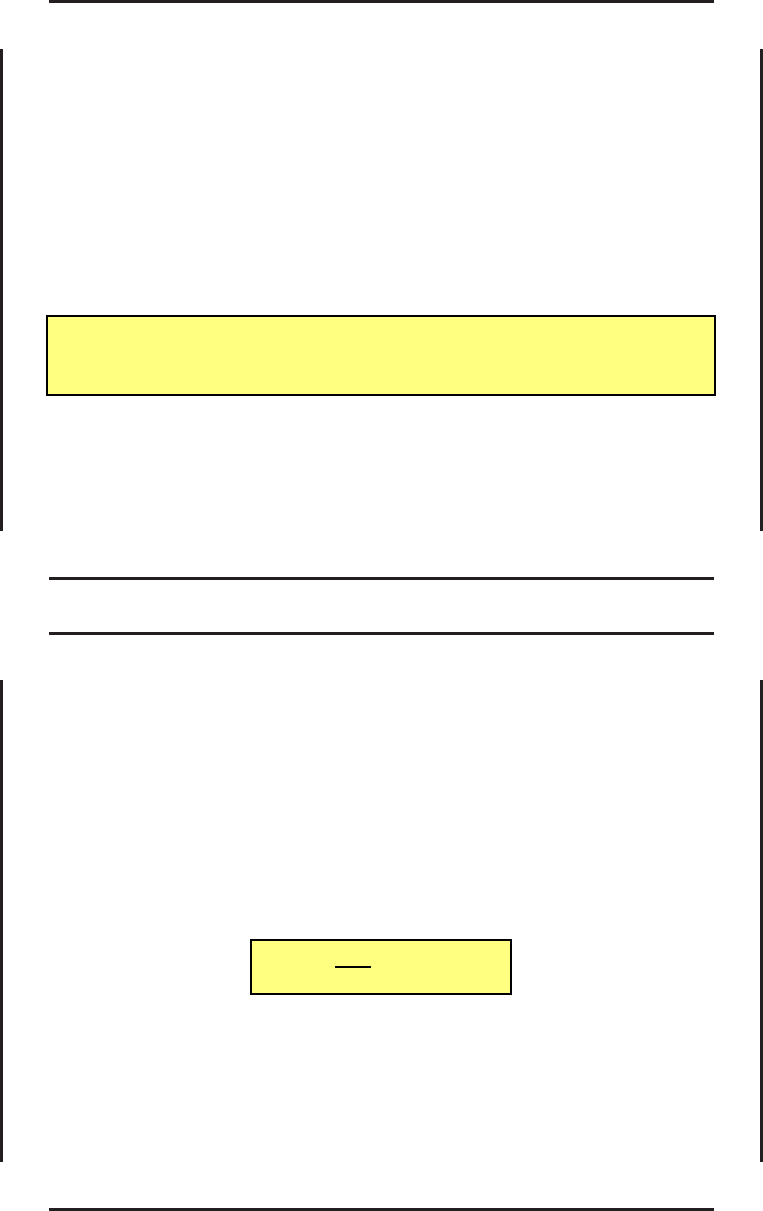
Необходимые условия минимума в задаче со свободным концом – 7

Итак, функции ˜x(t) и ψ(t) должны быть решением некоторой краевой задачи

для системы дифференциальных уравнений порядка 2n, которую мы получим,

если определим u(t) из условия стационарности (42)

ψf

− F

= 0,

то есть

u = ˜u(x, ψ, t),

после чего подставим фун кцию u в уравнения (26)

˙x = f(x, u, t),

и (45)

ψ = −f

∗

ψ + F

= −

∂H

∂x

Ю. В. Тюменцев 18

Оптимальное управление

Slide 37

Необходимы е условия оптимальности в задачах

программирования траекторий (XV)

Задачи классического вариационного исчисления – 15

Необходимые условия минимума в за д аче со свободным концом – 8

Получим в итоге:

˙x = f(x, ˜u(x, ψ, t), t) =

f(x, ψ, t),

ψ = −f

∗

(x, ˜u(x, ψ, t), t)ψ + F

(x, ˜u(x, ψ, t), t) =

ψ(x, ψ, t).

Порядок этой системы равен 2n, для отыскания требуемого решения имеется

также 2n условий: на левом конце задан о n компонент фаз ового вектора x(t

на правом конце — значения сопряженных переменных ψ(T ) = 0.

Slide 38

Необходимы е условия оптимальности в задачах

программирования траекторий (XVI)

Принцип максимума Л. С. Понтрягина – 1

Постановка задачи – 1

В задаче Лагранжа классического вариационного исчисления необходимое

условие оптимальности состояло в том, что оптимальное управление должно

быть стационарной точкой функции Гамильтона H, т.е. удовлетворять

векторному уравнению

∂H

∂u

= 0.

Если решение этого уравнения единственно, то можно найти управление

u = ˜u(x, ψ, t), что дает возможность свести вариационную задачу к решению

некоторой краевой задачи для обыкновенных дифференциальных уравнений.

Основное предположение для за дачи Лагранжа — управление может

принадлежать всему пространству, т.е. на у правление не налагалось никаких

ограничений. В практических з адачах, однако, такие ограничения, как правило,

имеются.

Ю. В. Тюменцев 19

Оптимальное управление

Slide 39

Необходимы е условия оптимальности в задачах

программирования траекторий (XVII)

Принцип максимума Л. С. Понтрягина – 2

Постановка задачи – 2

Для задач с ограничениями на управления условия оптимальности,

предлагаемые классическим вариационным исчислением, непригодны.

Расширение этих условий было осуществлено Л.С.Понтрягиным и получило

наименование «принцип максимума».

Согласно принципу ма ксимума , оптимальное управление должно доставлять

функции Гамильтона максимальное значение.

Благодаря принципу максимума, редукция вариационной задачи к краевой

задаче получила широкое распространение и в настоящее время лежит в основе

большинства используемых вычислительных алгоритмов.

Slide 40

Необходимы е условия оптимальности в задачах

программирования траекторий (XVIII)

Принцип максимума Л. С. Понтрягина – 3

Постановка зад ачи – 3

Задача Л .С. Понтрягина. Определить вектор-функции ˜u(t) ∈ R

, ˜x(t) ∈ R

при t ∈ [t

, T ], доставляющие минимум функ ционалу

J = J(x, u) =

(x, u, t)dt (47)

при условиях

˙x = f(x, u, t), (48)

u ∈ G

, (49)

(x(t

), t

) ∈ E

, (x(T ), T ) ∈ E

. (50)

Здесь G

— некоторое замкнутое множество допустимых управлений, E

— заданные многообрази я (n + 1)-мерного пространства начальных и

конечных условий, а функции f

, f = (f

, f

, . . . , f

) и их частные

производные по x непрерывны по совокупности переменных.

Управление u(t) будем искать в к лассе кусочно-непрерывных функций.

Ю. В. Тюменцев 20