Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 41

Необходимы е условия оптимальности в задачах

программирования траекторий (XIX)

Принцип максимума Л. С. Понтрягина – 4

Постановка задачи – 4

Единственное внешнее отличие рассматриваемой задачи от задачи Лагранжа

состоит в появлении нового условия (49)

u ∈ G

Однако именно это делает задачу существенно более сложной. Осложнения

связаны с тем, что допустимые вариации управления должны удовлетворять

условию

u = ˜u + δu ∈ G

т.е. вариации управления теперь не произвольны, они должны удовлетворять

заданным ограничениям.

Slide 42

Необходимы е условия оптимальности в задачах

программирования траекторий (XX)

Принцип максимума Л. С. Понтрягина – 5

Постановка задачи – 5

В некоторых случаях задачу Понтрягина можно свести к задаче Лагранжа.

В частн ости, если управление u — скалярная величина, удовлетворяющая

неравенству

|u| 6 1,

то можно, например, произвести замену переменных

u = sin α.

При этом на α не накладывается ограничений типа неравенства.

Подход, предложенный Л.С.Понтрягиным, позволяет получить более сильные и

общие результаты, чем те, что основаны на классическом вариационном

исчислении. Они справедливы для любых замкнутых областей, в том числе и

тех, которые нельзя «раскрыть» с помощью различных искусственных приемов.

Ю. В. Тюменцев 21

Оптимальное управление

Slide 43

Необходимы е условия оптимальности в задачах

программирования траекторий (XXI)

Принцип максимума Л. С. Понтрягина – 6

Игольчатое варьирование управления

Центральное понятие, позволяющее построить необходимые условия мини мума в задаче

Понтрягина — это понятие игольчатого варьирования управления (игольчатой вариации).

Будем называть управление ˜u(t) допустимым, е с-

ли ˜u(t) — кусочно-непрерывная функция со зна-

чениями из G

Пусть ˜u(t) — некоторое допустимое управление,

а ˜x(t) — соответствующая фазовая траектория.

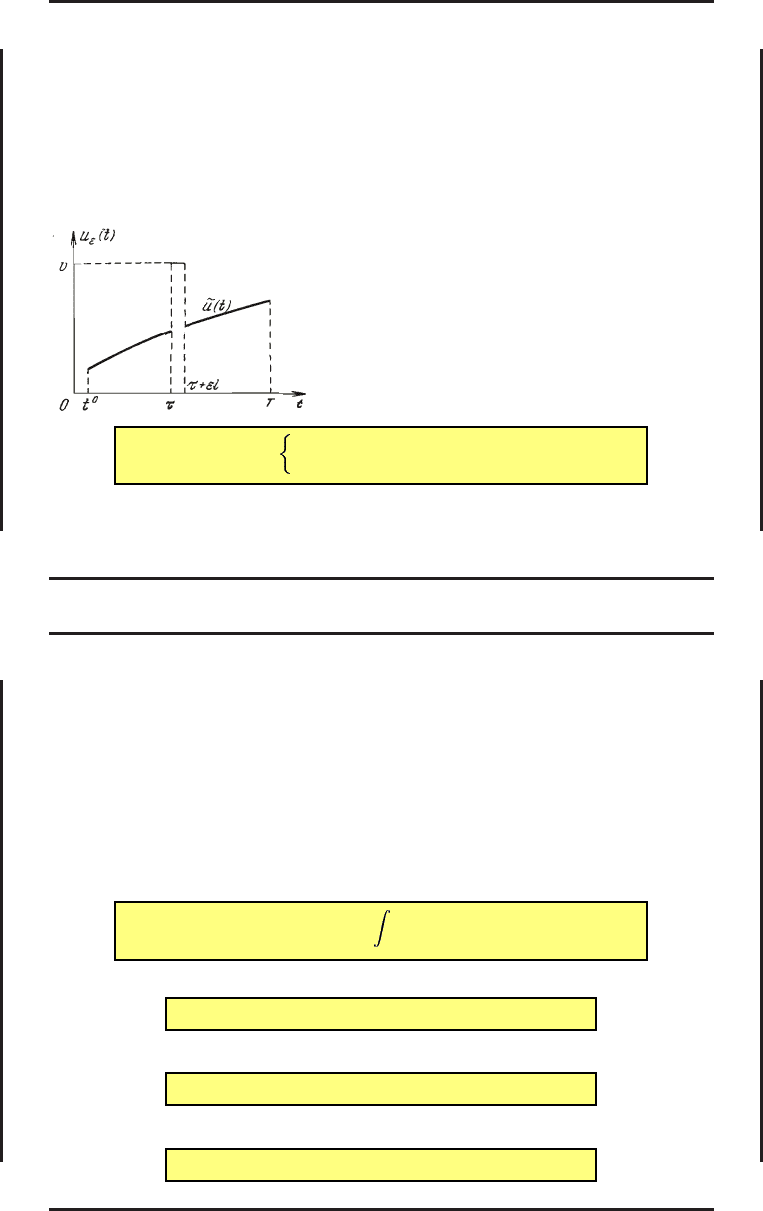
Игольчатым варьированием управ ления будем

называть следующую конструкцию (см. рис.):

(t) =

v, если t ∈ [τ, τ + εl],

˜u(t), если t /∈ [τ, τ + εl],

(51)

где τ — заданная точка непрерывности функции ˜u(t), l — заданное положительное число, ε

— произвольное положительное число такое, что t

< τ + εl < T , а постоянная v такова,

что v ∈ G

. Разность u

(t) − ˜u(t) = δu(t) будем называть игольчатой вариацией

управления.

Slide 44

Необходимы е условия оптимальности в задачах

программирования траекторий (XXII)

Принцип максимума Л. С. Понтрягина – 7

Вариации траектории – 1

Рассмотрим задачу, в которой левый конец траектории фиксирован, т.е. заданы значения

величин t

и x(t

) = x

. Нас интересует результат воздействия на траекторию со

стороны игольчатых вариаций управления.

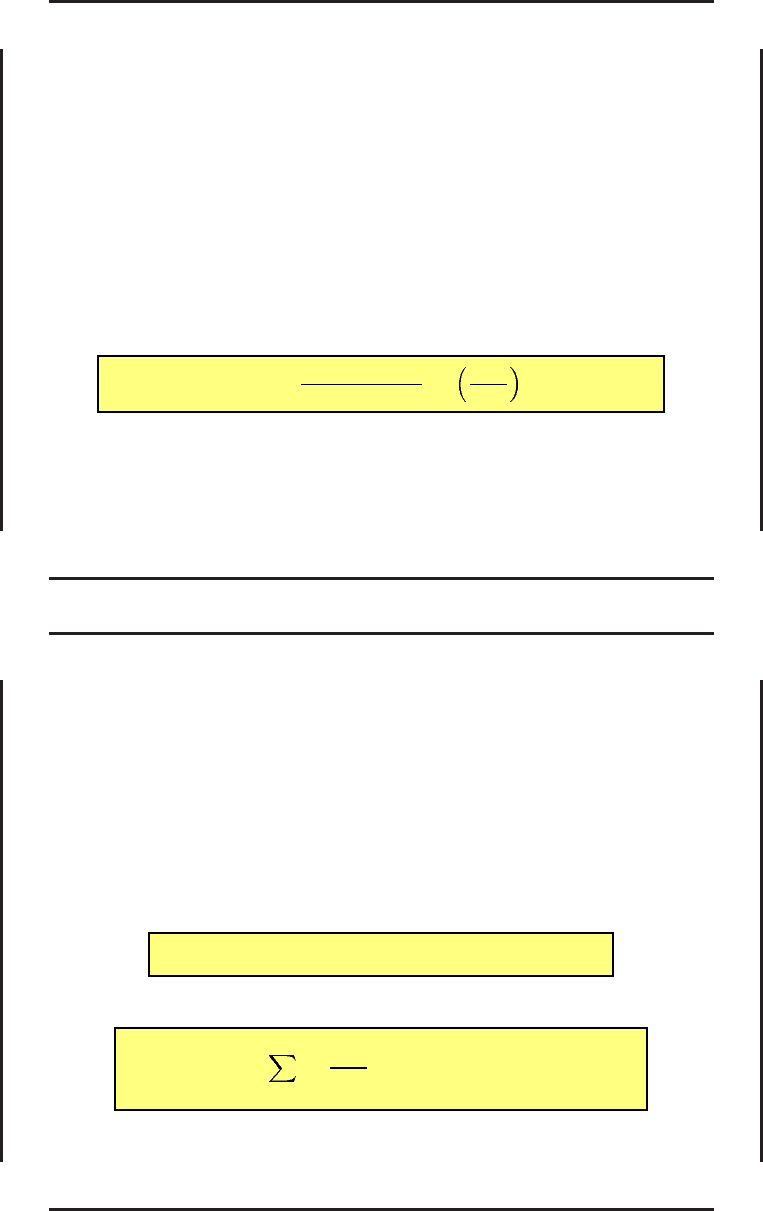
Для дальне йшего удобно вместо функционала (47)

J = J(x, u) =

(x, u, t)dt

ввести эквивалентное ему уравнение

˙x

= f

(x, u, t); x

) = 0

и рассматривать расширенный фазовый вектор

x = (x

, x

, . . . x

) ≡ (x

, x)

и расширенный вектор правых частей уравнений движения объекта

f = (f

, f

, . . . f

) ≡ (f

, f ).

Ю. В. Тюменцев 22

Оптимальное управление

Slide 45

Необходимы е условия оптимальности в задачах

программирования траекторий (XXIII)

Принцип максимума Л. С. Понтрягина – 8

Вариации траектории – 2

Введем ва риацию фазового вектора таким же способом, как и для задачи

Лагранжа, но для расширенного вектора x.

Обозначим через x

фазовую траекторию, соответствующую управлению u

после чего можно определить вариацию фазовой траектории:

h(t) = lim

ε→0

(t) − ˜x(t)

dε

ε=0

где ˜x — траектория, соответствующая рассматриваемому управлению ˜u.

Содержательный смысл вариации h(t) состоит в том, что при ε → 0

выражение εh(t) является главной линейной частью при ращения фа зовой

траектории, возникающего вследствие игольчатого варьирования управления.

Slide 46

Необходимы е условия оптимальности в задачах

программирования траекторий (XXIV)

Принцип максимума Л. С. Понтрягина – 9

Сопряженна я система – 1

Введем теперь сопряженную систему:

ψ = −f

∗

ψ (52)

или, в координатной форме,

= −

j=0

∂f

∂x

, i = 0, 1, 2, . . . , n.

Ю. В. Тюменцев 23

Оптимальное управление

Slide 47

Необходимы е условия оптимальности в задачах

программирования траекторий (XXV)

Принцип максимума Л. С. Понтрягина – 10

Задача со свободным правым концом и фиксированным временем

(1)

Пусть множество E

состоит из единственной точки (t

, x

), а множество E

—

гиперплоскость t = T, т.е.

x(t

) = x

, t

, T заданы. (53)

Пусть ˜u(t) — оптим ально е управление, а ˜x(t) — соответствующая

оптимальная траектория для рассматриваемой задачи.

Из необходимого условия минимума функционала, состоящего в

неотрицательности его первой вариации, получаем неравенство

(t) > 0. (54)

Основная идея дальнейшего вывода принципа максимума состоит в том, что

значение вариации функционала h

(t) связывается с некоторым выражением,

определенным на траектории. Эта связь и содержит в себе требуемые

необходимые условия оптимальности.

Slide 48

Необходимы е условия оптимальности в задачах

программирования траекторий (XXVI)

Принцип максимума Л. С. Понтрягина – 11

Задача со свободным правым концом и фиксированным временем

(2)

При этом сопряженная вектор-функция должна подчиняться следующему

условию:

= −1, ψ

(T) = 0, i = 1, 2 , . . . , n. (55)

Вектор ψ(t) будем рассматривать как решение уравнения (52) (сопряженная

система)

ψ = −f

∗

при «нач альном условии» (55).

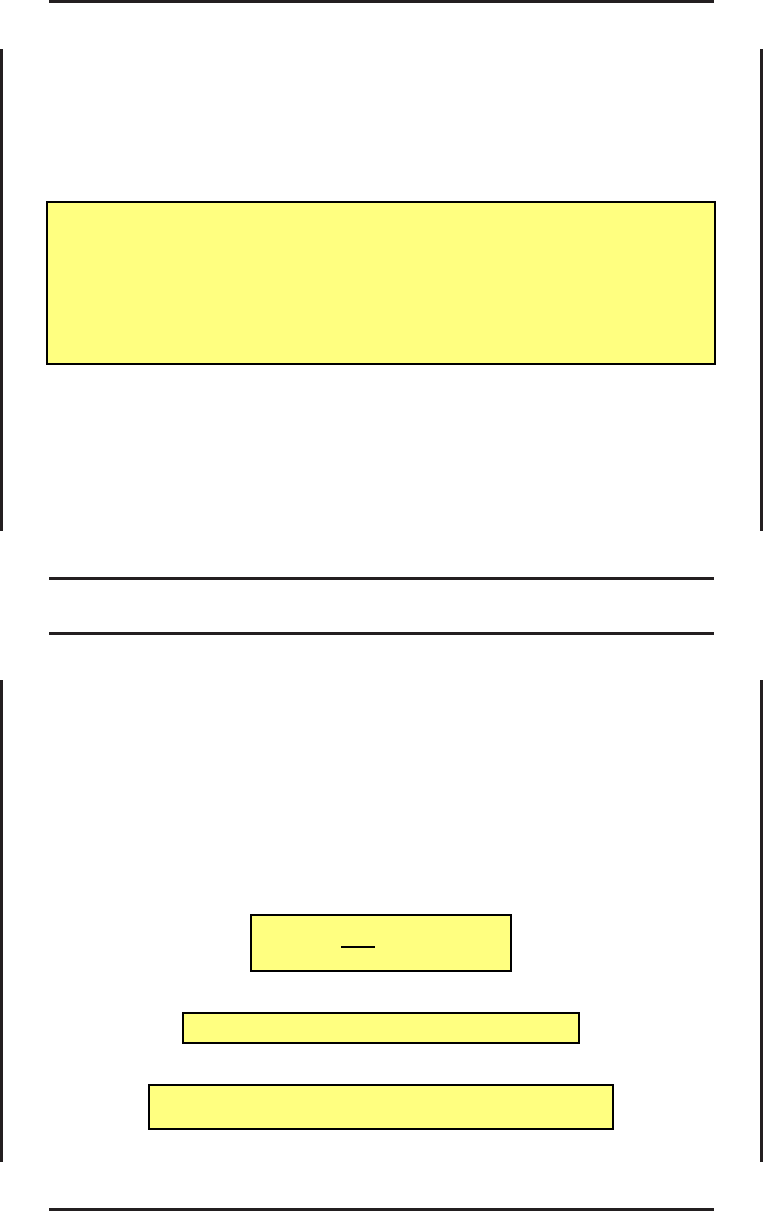
Соответствующая фу нк ция Гами льтона, требуемая для формулирования условий

оптимальности, будет иметь следующий вид:

H = (ψ, f) =

i=0

(x, u, t). (56)

Ю. В. Тюменцев 24

Оптимальное управление

Slide 49

Необходимы е условия оптимальности в задачах

программирования траекторий (XXVII)

Принцип максимума Л. С. Понтрягина – 12

Задача со свободным правым концом и фиксированным временем

(3)

Теорема. Если у правление ˜u(t) и траектория ˜x(t) доставляют минимум

функционалу (47) при уравнениях связи (48), ограничениях на управление

(49) и краевых условиях (53), то существует такая непрерывная вектор-

функция ψ = (ψ

, ψ

, . . . , ψ

), удовлетворяющая сопряженной систе-

ме (52) и условиям трансверсальности (55), что при каждом t ∈ [t

, T ]

функция Гамильтона H(˜x(t), ˜u(t),

ψ(t), t) (56) достигает в точке ˜u(t)

максимума по всем u ∈ G

В рассматриваемой задаче с фиксированным временем T и свободным правым

концом x(T ) условия трансверсальности (55) требуют, чтобы, как и в задаче

Лагранжа, при t = T зна чение нулевой компоненты ψ

(T) было равно −1, а

значение остальных компонент равнялось б ы нулю.

Поскольку условия трансверсальности в задачах Лагранжа и Понтрягина одни и

те же, то структура краевой задачи, которой должно удовлетворять оптимальное

решение, в обоих случаях остается одинаковой.

Однако системы уравнений могут быть различными.

Slide 50

Необходимы е условия оптимальности в задачах

программирования траекторий (XXVIII)

Принцип максимума Л. С. Понтрягина – 13

Задача со свободным правым концом и фиксированным временем

(4)

Указанное различие между системами уравнений, для которых требуется решать

полученную краевую задачу, состоит в следующем.

Рассматривая задачу Лагранжа, мы получали управление при помощи условия

стационарности

∂H

∂u

= 0

как функцию от фазовых и сопряженных переменных

u = ˜u(x, ψ, t).

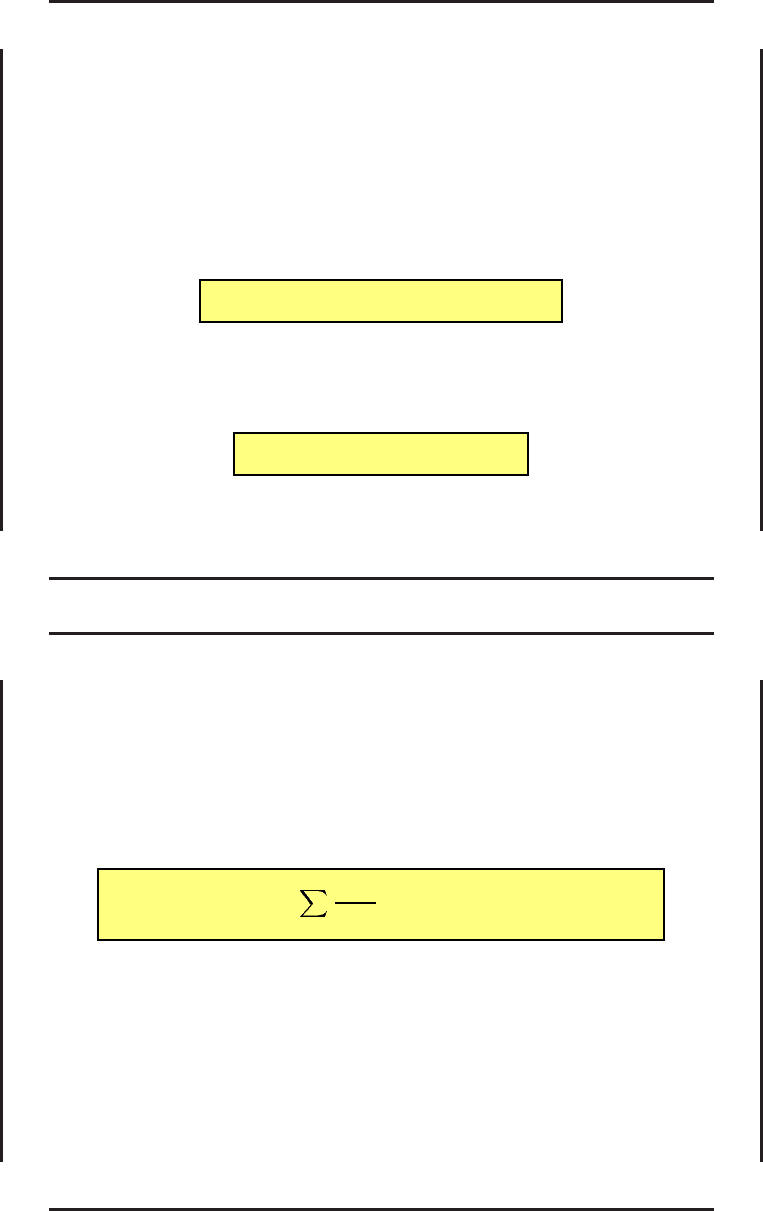
В задаче Понтрягина мы проделали ту же процедуру, но с помощью условия

H = max

u∈G

H(x, u, ψ, t).

Конечно, в том случае, когда G

совпадает со всем пространством управлений, а функция

H имеет одну экстремальную точку, которая при этом является максимумом, оба условия

дадут одну и ту же функцию ˜u(x, ψ, t).

Ю. В. Тюменцев 25

Оптимальное управление

Slide 51

Необходимы е условия оптимальности в задачах

программирования траекторий (XXIX)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 1

Рассмотрим простейшие виды неклассических вариацио нны х задач, в которых

область N > 0 определяется лишь условием

||u|| 6 ¯u, (57)

где ¯u — заданное число, физ ический смысл которого состоит в ограниченности

ресурсов (например, энергетических) объекта у правления.

Пусть имеются уравнения движения вида:

˙z = ω(z, u),

где функции ω

дважды дифференцируемы по всем аргументам.

Slide 52

Необходимы е условия оптимальности в задачах

программирования траекторий (XXX)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 2

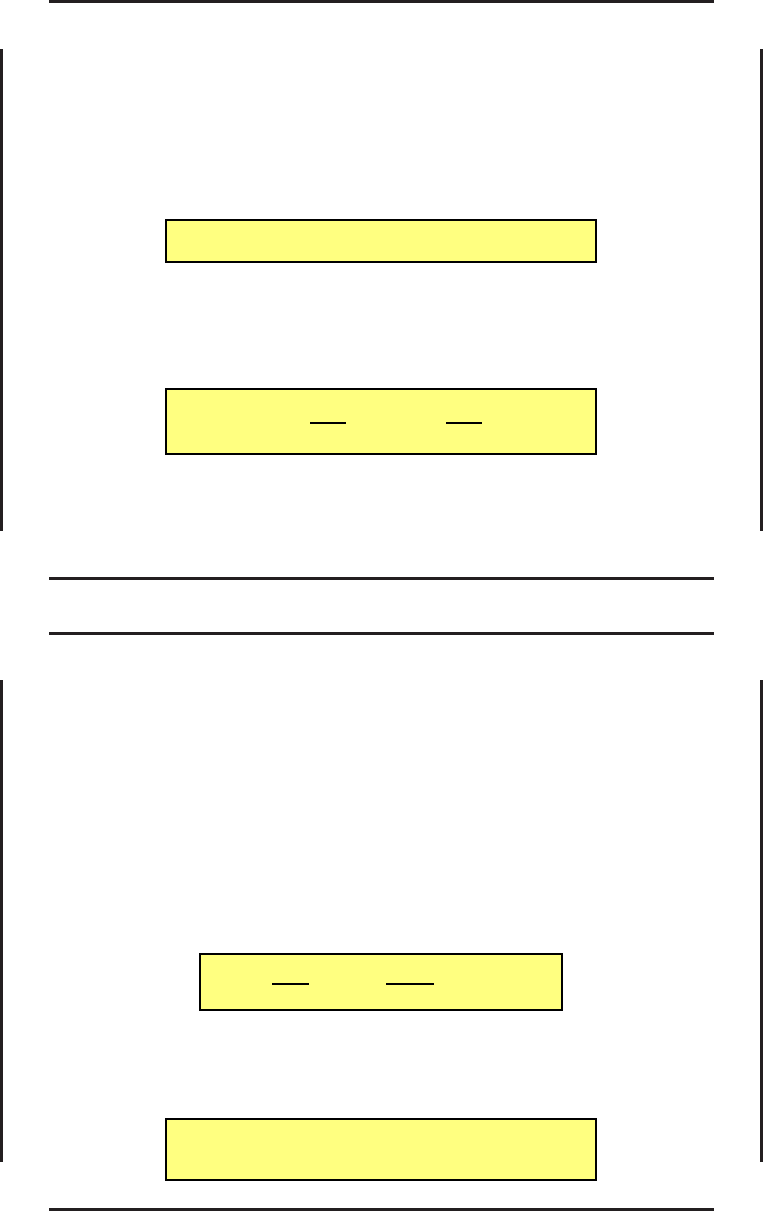
Определим вспомогательный вектор Ψ как решение уравнений

= −

∂ω

∂z

, k = 1, . . . , n. (58)

Вектор ψ — совершенно ненулевой, если ни одна из его компонент не равна

тождественно нулю при t ∈ T .

Пусть u — любое допустимое управление, а z — соответствующая допустимая

траектория. Тогда ∂ω

/∂z

— непрерывные функции времени t, они линейны и

однородны.

Решение — вектор ψ, являющийся непрерывной кусочно-гла дкой функцией при

любом t ∈ T .

Ю. В. Тюменцев 26

Оптимальное управление

Slide 53

Необходимы е условия оптимальности в задачах

программирования траекторий (XXXI)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 3

Рассмотрим вспомогательную функцию

H(ψ, z, u) = ψ · ω. (59)

Она зависит от трех векторных аргументов: ψ, z, u. Функция H играет важную

роль в дальнейших построениях. Так, например, она позволяет представить

уравнения модели и уравнения для вектора ψ в более компактной и симметричной

форме:

˙z =

∂H

∂ψ

ψ = −

∂H

∂z

. (60)

Кроме того, как будет показано далее, оптимальное управление в этом случае

находится весьма просто — путем исследования функции H на максимум по

переменной u при фиксированных остальных переменных.

Slide 54

Необходимы е условия оптимальности в задачах

программирования траекторий (XXXII)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 4

Пусть поиск опт имального управления осуществляется путем исследования

функции H на максимум по переменной u при фиксированных остальных

переменных.

Если соответствующее значение переменной u не достигает границ области

N > 0, то м аксимум фу нкции H понимается в обычном, классическом смысле:

∂H

∂u

= 0,

∂

∂u

< 0.

Если же u достигает границ области N > 0, то максимум функции H следует

определять как точную верхнюю грань функции H по u.

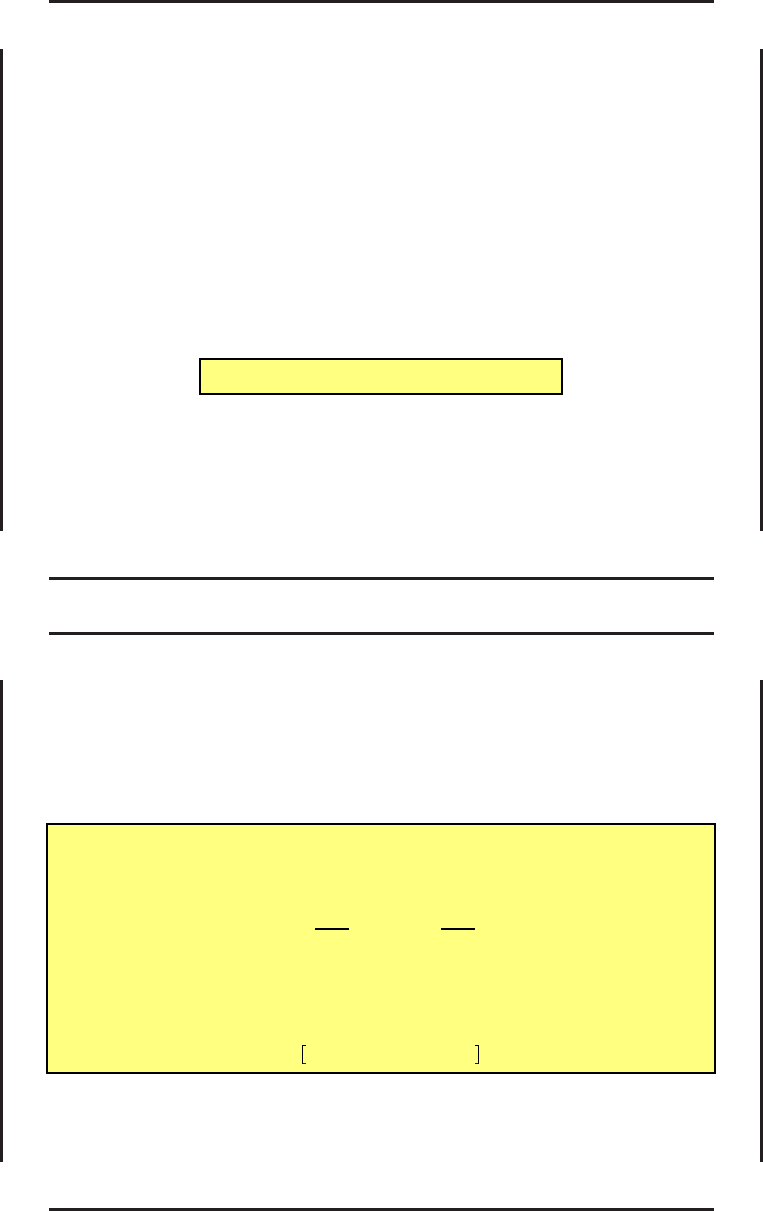
Этом максимум обозначим как

M(ψ, z) = max

u∈U

H(ψ, z, u). (61)

Ю. В. Тюменцев 27

Оптимальное управление

Slide 55

Необходимы е условия оптимальности в задачах

программирования траекторий (XXXIII)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 5

Принцип макс и мума дает необходимое условие сильного экстремума

функционала для значительно более широких классов функций сравнения и более

сложных видов ограничений области N, чем те, что определяются неравенством

||u|| 6 ¯u,

Однако трактовка проблемы оптимального управления в таком виде чрезвычайно

трудна, поэтому ограничимся более простым частным случаем задачи Майера.

Slide 56

Необходимы е условия оптимальности в задачах

программирования траекторий (XXXIV)

Принцип максимума Л. С. Понтрягина (предыдущая

формулировка) – 6

Пусть u

, z

— экстремаль. Один из важнейших результатов теории оптимального

управления, принцип максимума, сформулированный Л. С. Понтрягиным, применительно к

задаче Майера выражается следующей теоремой.

Теорема. Для того, чтобы кривая u

, z

доставляла сильный минимум функци он алу

в задаче Майера, необходимо существование соверш енно ненулевого непрерывного

вектора ψ = (ψ

, . . . , ψ

), определяемого урав нениями (60)

˙z =

∂H

∂ψ

ψ = −

∂H

∂z

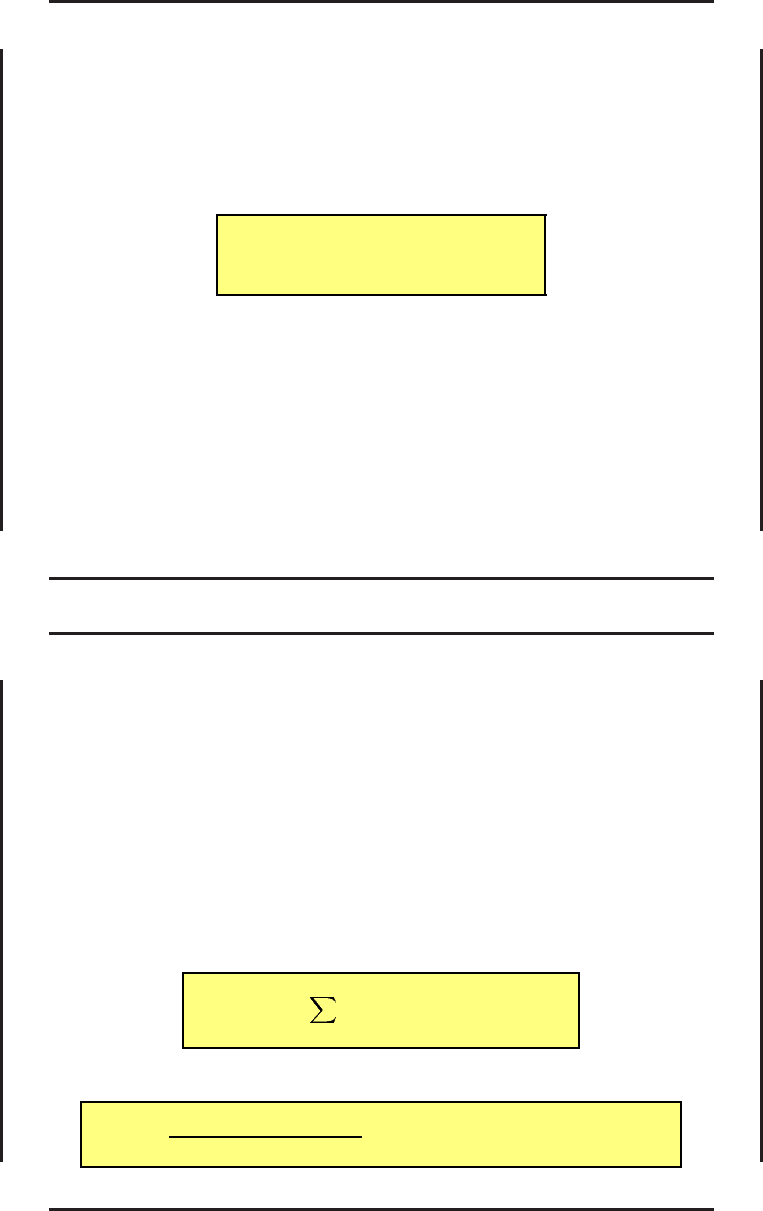
при этом для вектора ψ должны удовлетворяться следующие условия:

1) функция H(ψ, z, u) = ψ · ω достигает максимума по u,

2) выполняется условие трансверсальности

δG − Hδt + ψ · δt

. (62)

Если функции G и H линейны по z, u, условия существования сильного минимума,

оговоренные в данной теореме, являются также и достаточными.

Вектор ψ — совершенно ненулевой, если ни одна его компонента не равна тождественно

нулю при любых t ∈ T .

Условие тр а нсве рсальности на кладывается на вариации концов кривых сравнения.

Ю. В. Тюменцев 28

Оптимальное управление

Slide 57

Численные методы в теории оптимальных систем —

общие положения

Различные методы отыскания экстремума ф ункции или функционала

f (x ) принято разделять на две большие группы:

❑ прямые методы,

❑ непрямые методы.

Прямые методы — все методы градиентного спуска и родственные им.

Основаны на просмотре окрестности некоторой точки x

, позволяющем

найти другую точку x

n+1

, в которой значение функции f (x

n+1

) будет

меньше f (x

). Эти методы не используют непосредственно

необходимых и достаточных условий экстремума.

Непрямые методы направлены на отыскание функции f(x),

непосредственно удовлетворяющей необходимым или достаточным

условиям экстремума.

Slide 58

Численные методы в теории оптимальных систем —

прямые методы

Прямые методы оптимального управления — все те методы, которые

непосредственно не используют необходимых условий оптимальности.

Пример — метод Ритца.

Схема метода: требуется отыскать минимум функционала J(y), y ∈ Y , где Y

— некоторое множество, например, множество дифференцируемых функций.

Решение задачи отыскивается в виде

y =

i=1

, ϕ

∈ Y.

Задача определения постоянных λ

сводится к решению сис т е мы уравнений:

∂J(λ

, λ

, . . . , λ

)

∂λ

= 0, i = 1, 2, . . . , N.

Ю. В. Тюменцев 29

Оптимальное управление

Slide 59

Численные методы в теории оптимальных систем —

непрямые методы

Непрямые методы направ лены на отыскание функции f(x),

непосредственно удовлетворяющей необходимым или

достаточным условиям экстремума.

Задача отыскания минимума с помощью необходимых условий

сводится:

❑ для функции — к задаче отыскания ее корней,

❑ для функционала (отыскание оптимальной про-

граммы) — к решению краевой задачи для систе-

мы обыкновенных дифференциальных уравнений.

Slide 60

Численные методы в теории оптимальных систем —

непрямые методы

Основное достоинство непрямых методов — простота вычислительной

реализации.

Важнейшие недостатки непрямых методов:

❑ задача становится практически неразрешимой, ко-

гда необходимые условия формулируются относительно

сложно (например, в случае фазовых ограничений);

❑ функция или точка, удовлетворяющая необходимым

условиям — это всего лишь претендент на право на зы-

ваться решением (требуется еще проверка достаточных

условий).

Попытки строить вычислительные процедуры, опираясь сразу на

достаточные условия, не прибегая к необходимым, не дают

удовлетворительных р езультатов.

На практике — целесообразно сочетание прямых и непрямых методов.

Ю. В. Тюменцев 30