Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 341

Адаптивное управление с эталонной модель ю (XV)

Компенсирующий контур в адаптивном управлении с ЭМ – 3

0 5 10 15 20 25 30 35 40 45

α, deg

MRAC with compensator

0 5 10 15 20 25 30 35 40 45 50

−0.2

0.2

, deg

0 5 10 15 20 25 30 35 40 45 50

−5

ref

, deg

0 5 10 15 20 25 30 35 40 45 50

−10

act

, deg

t, sec

Plant

RefModel

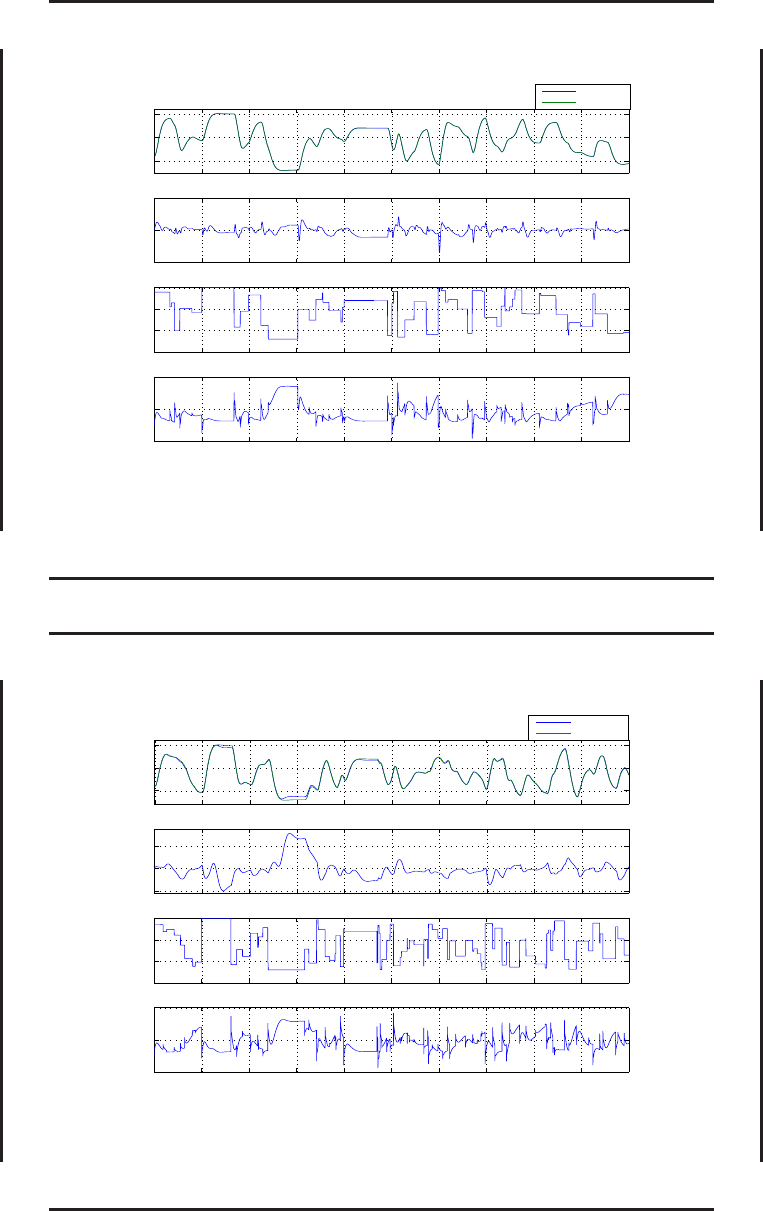
Результаты вычислительного эксперимента для системы управления с эталонной моделью и

компенсатором (ГЗЛА X-43, режим полета M = 6). Обозначения: α — угол атаки, гр ад;

— ошибка отслеживания заданного угла атаки, гр ад; α

ref

— задающий сигна л по углу

атаки, град; φ

act

— командный сигнал для привода элевонов, град.; t — вре мя, с; Plant —

объект управления; RefModel — эталонная модель.

Slide 342

Адаптивное управление с эталонной модель ю (XVI)

Компенсирующий контур в адаптивном управлении с ЭМ – 4

0 5 10 15 20 25 30 35 40 45

α, deg

MRAC without compensator

0 5 10 15 20 25 30 35 40 45

−0.5

0.5

, deg

0 5 10 15 20 25 30 35 40 45 50

−5

ref

, deg

0 5 10 15 20 25 30 35 40 45 50

−10

act

, deg

t, sec

Plant

RefModel

Результаты вычислительного эксперимента для системы управления с эталонной моделью и

без компенсатора (ГЗЛА X-43, режим полета M = 6). Обозначения: α — угол атаки, град;

— ошибка отслеживания заданного угла атаки, гр ад; α

ref

— задающий сигна л по углу

атаки, град; φ

act

— командный сигнал для привода элевонов, град.; t — вре мя, с; Plant —

объект управления; RefModel — эталонная модель.

Ю. В. Тюменцев 171

Оптимальное управление

Slide 343

Адаптивное управление с ЭМ (XVII)

Вычислительный эксперимент – 1

2 4 6 8 10 12

−5

α, deg

0 2 4 6 8 10 12

−0.1

0.1

, deg

0 2 4 6 8 10 12

−5

ref

, deg

0 2 4 6 8 10 12

−10

act

, deg

t, sec

Plant

RefModel

Результаты вычислительного эксперимента для системы управления с эталонной моделью и

компенсатором при ступенчатом изменении задающего сигнала (ГЗЛА X -43, режим полета

M = 6). Обозначения: α — угол атаки, град.; e

— ошибка отслеживания заданного угла

атаки, град.; α

ref

— задающий сигна л по углу атаки, град.; φ

act

— командный сигнал для

привода элевонов, град.; t — время, с; Plant — объе кт управления; RefModel — эталонная

модель.

Slide 344

Адаптивное управление с ЭМ (XVIII)

Вычислительный эксперимент – 2

0 10 20 30 40 50 60 70 80

−20

−10

α, deg

dXt=+0.1 at t=30s, Mzfi−50% at t=50s, online training

10 20 30 40 50 60 70 80

−2

−1

∆α, deg

0 10 20 30 40 50 60 70 80

−20

−10

φ, deg

t, sec

Object

RefModel

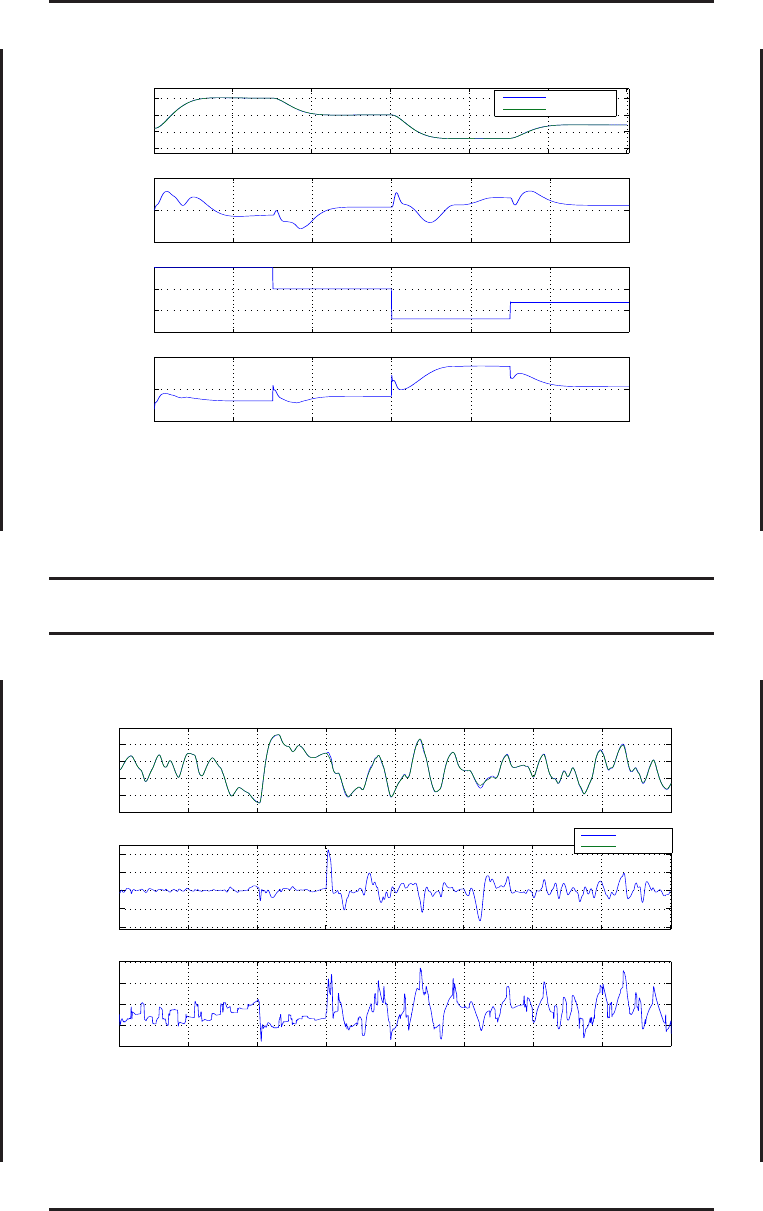
Результаты вычислительного эксперимента для системы управления с эталонной моделью и

компенсатором (самолет F-16, режим полета с и ндикаторной скоростью V

ind

= 600 к м/ч).

Адаптация к изменению динамики объекта управления: сме щ ение центровки на 10% назад

(t = 30 с), 50% уменьшение эффективности органа управления (t = 50 с). Обозначения: α

— угол атаки, град.; ∆α — ошибка отслеживания заданного угла атаки, град.; φ — угол

отклонения стабилизатора, град.; t — время, с; Plant — объект управления; RefModel —

эталонная модель.

Ю. В. Тюменцев 172

Оптимальное управление

Slide 345

Адаптивное управление с ЭМ (XIX)

Вычислительный эксперимент – 3

0 10 20 30 40 50 60 70 80 90 100

−20

−10

α, deg

dXt=+0.1 at t=30s, dMzFi−50% at t=60s, online training

10 20 30 40 50 60 70 80 90 100

−1

−0.5

0.5

∆α, deg

0 10 20 30 40 50 60 70 80 90 100

−20

−10

φ, deg

t, sec

Object

RefModel

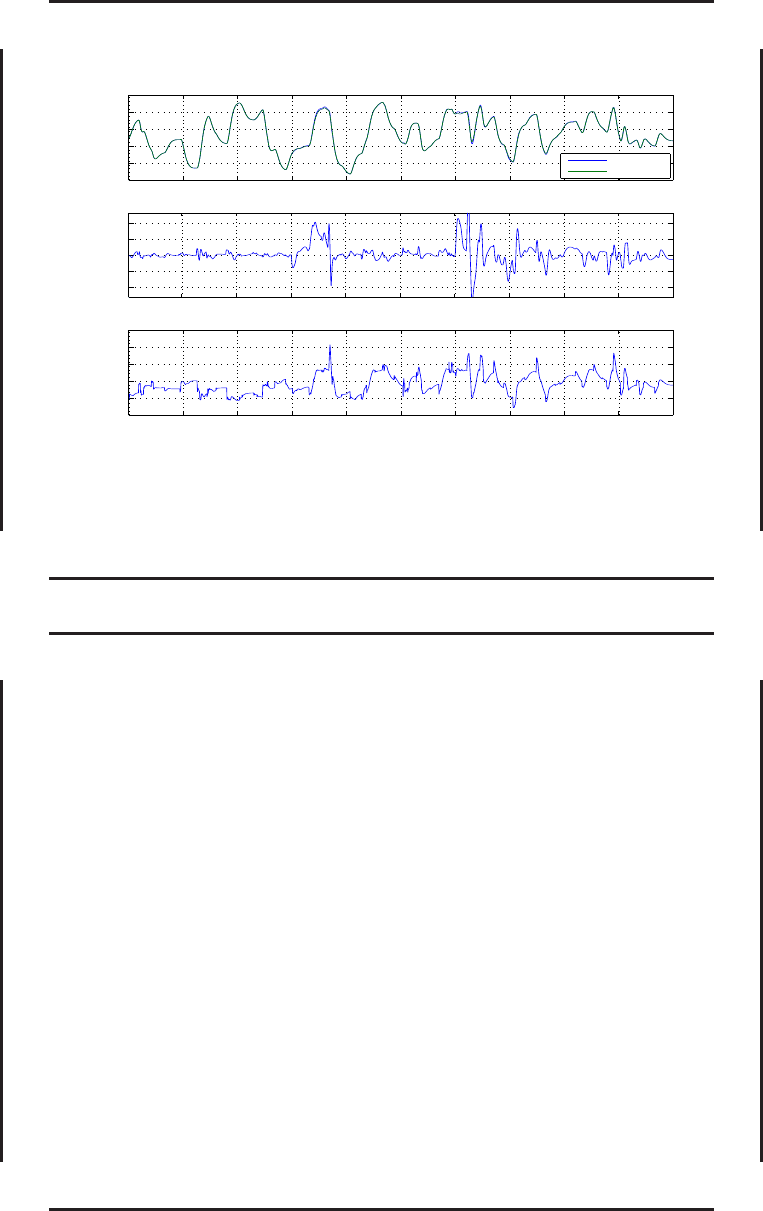
Результаты вычислительного эксперимента для системы управления с эталонной моделью и

компенсатором (самолет F-16, режим полета с и ндикаторной скоростью V

ind

= 700 к м/ч).

Адаптация к изменению динамики объекта управления: сме щ ение центровки на 10% назад

(t = 30 с), 50% уменьшение эффективности органа управления (t = 60 с). Обозначения: α

— угол атаки, град.; ∆α — ошибка отслеживания заданного угла атаки, град.; φ — угол

отклонения стабилизатора, град.; t — время, с; Plant — объект управления; RefModel —

эталонная модель.

Slide 346

Адаптивное управление с ЭМ (XX)

Вычислительный эксперимент – 4

Было показано, как адаптивная система управления с ЭМ и компенсатором

справляется с влиянием двух последовательных отказов, существенно

влияющих на динамику объекта.

Первый из них приводит к смещению центровки на 10% назад (при t = 20 с),

второй — к уменьшению на 50% эффективности органа управления продольным

движением (при t = 50 с).

Видно, что использованная схема адаптации обеспечивает работу с

незначительной ошибкой (e

≈ ±0.05 град) до м омента возникновения первой

отказной ситуации.

Адаптация к изменению динам и ки объекта, вызванному этой ситуацией,

происходит достаточно быстро (примерно за 1.2–1.5 с).

Ошибка теперь (до момента возникновения второй отказной ситуации) стала

больше, но она укладывается, в основном, в диапазон e

≈ ±0.2 град,

устойчивость работы системы сохранена.

После второго отказа устойчивость сохранена, н о значения ошибки становятся

довольно значительными (e

≈ ±0.5 град).

Ю. В. Тюменцев 173

Оптимальное управление

Slide 347

Адаптивное управление с ЭМ (XXI)

Вычислительный эксперимент – 5

Задающий сигнал по углу атаки, отслеживание которого должна обеспечить

рассматриваемая система управления, строился по тем же правилам, что и

командный сигнал привода органа управления при формировании обучающего

набора для НС-модели.

А именно, формировалась случайная последовательность ступенчато

изменяемых отслеживаемых значений угла атаки, при частых и существенных

перепадах между соседними значениями элементов данной последовательности.

Такой подход призван обеспечить возможно большее разнообразие состояний

моделируемой системы (чтобы покрыть по-возможности равномерно и плотно все

пространство состояний системы), а также возможно большее разнообразие

перепадов состояний, соседних по времени (чтобы максимально достоверно

отразить в алгоритме управления, реализуемом НК, динамику объекта).

Slide 348

Адаптивное управление с ЭМ (XXII)

Вычислительный эксперимент – 6

Итак, можно заключить: представленные результаты вычислительных

экспериментов убедительно показывают, что в подавляющем большинстве случаев

адаптивная нейросетевая система управления с ЭМ успешно справляется со

своими задачами.

В том числе она вполне удовлетворительно работает и при возникновении

отказных ситуаций.

Ю. В. Тюменцев 174

Оптимальное управление

Slide 349

Адаптивное управление с ПМ (I)

Общая схема адаптивного управления с ПМ – 1

В за даче управления с прогнозирующей моделью (MPC — Model Predictive Control)

используется модель объекта, с помощью которой прогнозируется его будущее поведение,

а также оптимизационный алгоритм для выбора управляющего воздействия, обеспечивающего

наилучшие значения прогнозируемых характер истик рассматриваемой системы.

Управление с прогнозирующей моделью основывается на методе скользящего горизонта,

согласно которому НС-модель предсказывает выход объекта управления через заданный

промежуток времени (горизонт прогноза).

Полученные результаты прогноза используются алгоритмом численной оптимизации для того,

чтобы найти значени е управления u, которое минимизирует на заданном горизонте

прогноза следующий критерий качества управления:

J =

j=N

(t + j) − y

(t + j))

+ ρ

j=1

′

(t + j − 1) − u

′

(t + j − 2))

Здесь N

, N

и N

— числовые параметры, определяющие горизонт прогноза, в пределах

которого оцениваются значения ошибки слежения и приращений управляющего сигнала.

Величины (y

и y

— желаемый выход объек та управления и в ы ход НС-модели,

соответственно, u

′

— пробные управляющие воздействия, ρ — весовой коэффициент,

задающий относительную долю вклада отклонений по управлениям в общее значение

критерия эффективности J.

Slide 350

Адаптивное управление с ПМ (II)

Общая схема адаптивного управл ения с ПМ – 2

Объект

управления

Алгоритм

оптимизации

Компенсатор

Эталонная

модель

−

∗

доп

∗

эм

НС-модель

объекта

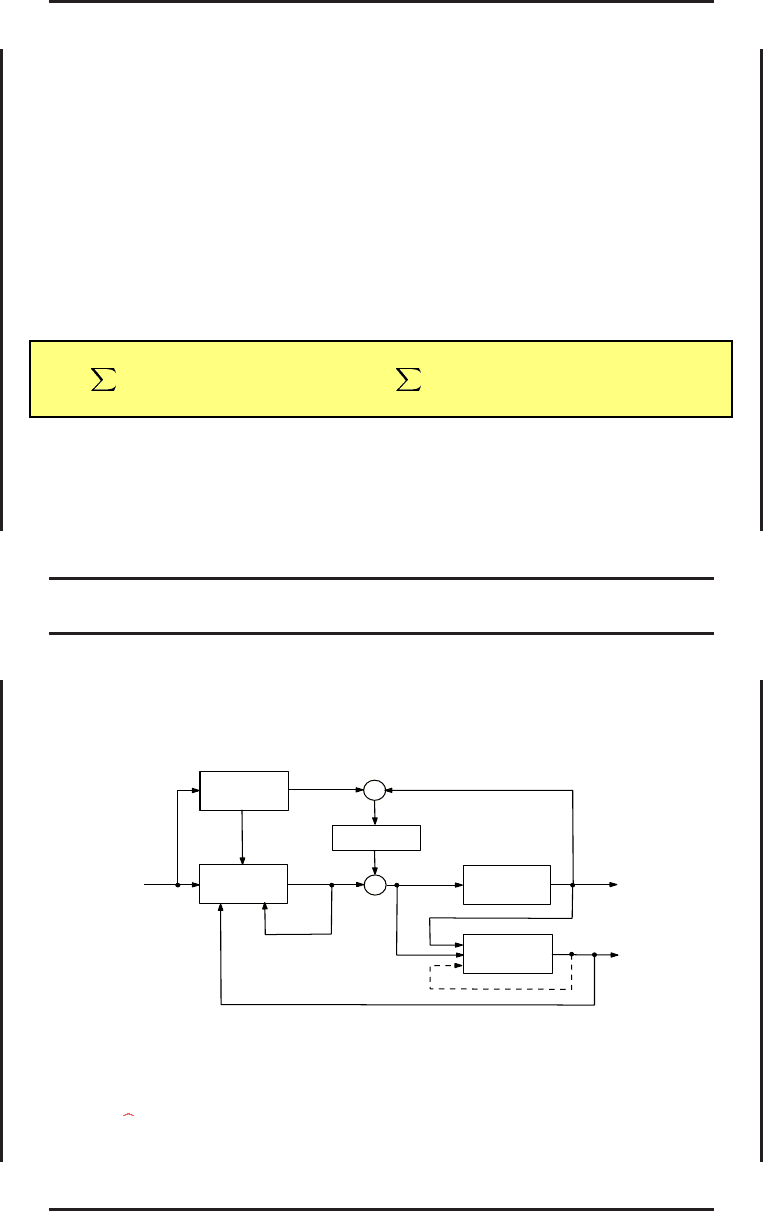
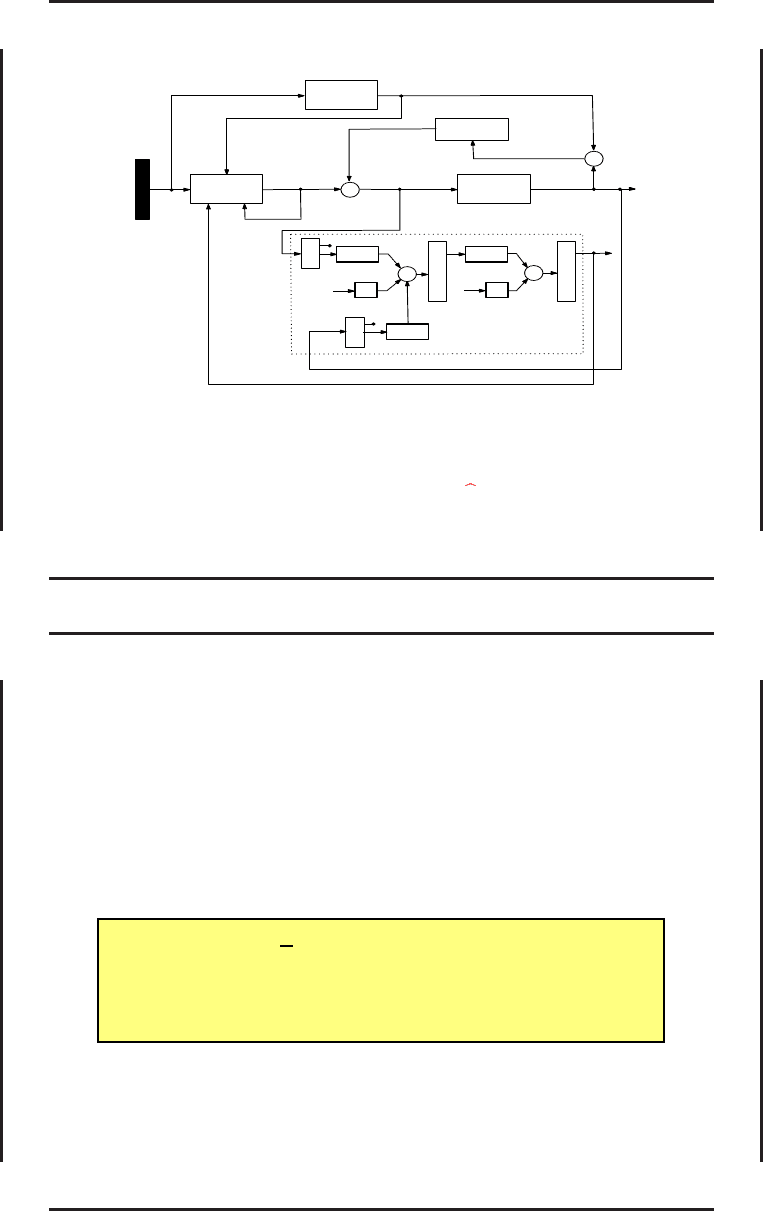
Схема нейросетевого адаптивного прогнозирующего управ л ения

Здесь обозначено: u

∗

— управление на выходе алгоритма оптимиз ации, u

доп

— добавочное

управление от компенсатора, u — результирующее управление, y

— выход объе к та

управления, y — выход нейросетевой модели объек та управления; y

эм

— выход эталонной

модели; ε — расхождение между выходами объекта управления и эталонной модели; r —

задающее воздействие

Ю. В. Тюменцев 175

Оптимальное управление

Slide 351

Адаптивное управление с ПМ (III)

Общая схема адаптивного управления с ПМ – 3

3,2

3,4

4,3

НС-модель

объекта

управления

r(t)

(t)

ε(t)

Объект

управления

(t)

−

доп

(t)

y(t)

Алгоритм

оптимизации

Эталонная

модель

Компенсатор

∗

(t)

∗

(t)

u(t)

(t)

y(t)

r(t)

(t)

Структурная схема нейросетевой реализации адаптивного управлен ия с П М: TDL — линия

задержки; IW — матрица весов связей между входным и первым обрабатывающим слоем НС;

LW — матрица весов связей между обрабатывающими слоями НС; b — набор смещений слоя

НС; f — набор активационных функций слоя НС; Σ — набор сумматоров слоя НС; n(t) —

набор скалярных выходов сумматоров; a(t) — набор скалярных выходов активационных

функций; r(t) — задающий сигнал; y

(t) — выход ОУ; y(t) — выход НС-модели; y

(t)

— выход ЭМ; u

∗

(t) — управление, вырабатываемое алгоритмом оптимизации; u

доп

(t) —

добавочное управление от компенсатора; u(t) — упра вление, поступающее на вход ОУ;

ε(t) = y

(t) − y

(t) — расхождение между выходами ОУ и ЭМ.

Slide 352

Адаптивное управление с ПМ (IV)

Синтез контроллера для адаптивного управления с ПМ – 1

В схеме с ПМ используется только одна многослойная нейронная сеть,

представляющая собой НС-модель объекта.

Контроллер здесь представлен алгоритмом оптимизации.

Критерием качества для данной системы является среднеквадратическая ошибка

на интервале прогноза (5–7 шагов):

E(u) =

e, e(u) = y − ˆy(u),

e = [e

k+2

, e

k+3

, . . . , e

k+T

]

u = [u

k+1

, u

k+2

, . . . , u

k+T −1

]

где T — длина интервала прогноза.

Таким образом, в схеме с ПМ выполняется минимизация отклонения поведения

НС-модели от ЭМ не по параметрам нейроконтроллера (и х тут нет вообще), а

непосредственно по управлению на интервале прогноза.

Ю. В. Тюменцев 176

Оптимальное управление

Slide 353

Адаптивное управление с ПМ (V)

Синтез контроллера для адаптивного управления с ПМ – 2

Контроллер в схеме управления с ПМ реализует оптимизационны й алгоритм

Гаусса-Ньютона

n+1

= u

+ (J

+ λE)

−1

где E — единичная матрица, J(w

) — якобиан ошибки по парам етрам, µ —

параметр подстройки.

Метод Гаусса-Ньютона очень похож на метод Левенберга-Марквардта,

отличается только тем, что коэффициент µ в нем не меняется динамически, он

выбирается экспериментально для решаемой задачи.

Slide 354

Адаптивное управление с ПМ (VI)

Синтез контроллера для адаптивного управления с ПМ – 3

Основная сложность — необходимо вычислить динамический якобиан по

управлению:

∂e

k+2

∂u

k+1

∂e

k+2

∂u

k+2

. . .

∂e

k+2

∂u

k+T −1

∂e

k+3

∂u

k+1

∂e

k+3

∂u

k+2

. . .

∂e

k+3

∂u

k+T −1

· · · · · · · · · · · ·

∂e

k+T

∂u

k+1

∂e

k+T

∂u

k+2

. . .

∂e

k+T

∂u

k+T −1

Для этого используется метод обратного распространения ошибки во вре мени

(BPTT — Back Propagation Through Time) для замкнутой нейросетевой модели.

Ю. В. Тюменцев 177

Оптимальное управление

Slide 355

Адаптивное управление с ПМ (VII)

Синтез контроллера для ад аптивного управления с ПМ – 4

С учетом сказанного, вычисление управления на каждом шаге интегрирования производится

в следующей последовательности:

1) Построение желаемого поведения на интервале прогноза. ЭМ просчитывается на этом

интервале при постоянном задающем сигнале (за дающий сигнал

k+1

. . . r

k+T −1

= r

: самый простой вариант — последнее доступное значение

этого сигнала).

2) Прогноз проведения объекта управления по его НС-модели на несколько шагов

вперед. На чальными условиями для модели являются эталонная траектория и

предыдущие значения управления, полученные с помощью такого контроллера.

3) Определение вектора ошибки следования, вы числен ие якобиана ошибки для каждого

момента времени по упра влению в каждый момент времени.

4) Корректировка вектора управления любым оптимизационным методом (в данном

случае методом Гаусса-Ньютона). Пункты 2–4 представляют собой одну итерацию

оптимизационной процедуры, выполняемой до разумного уме ньшения ошибки прогноза.

5) В качестве управления (в реальный объект) на следующем шаге (процедура

оптимизации занимает часть шага) берется первое упра вление на интервале прогноза

(т.е. u

k+1

). Этим же значением заполняется весь вектор н ачального приближения

управления на следующем шаге.

Slide 356

Адаптивное управление с ПМ (VIII)

Вычислительный эксперимент для управления с ПМ – 1

0 2 4 6 8 10 12 14 16 18 20

−5

α, deg

MPC without failures

0 2 4 6 8 10 12 14 16 18 20

−0.5

0.5

, deg

0 2 4 6 8 10 12 14 16 18 20

−5

ref

, deg

2 4 6 8 10 12 14 16 18 20

−10

act

, deg

t, sec

Plant

RefModel

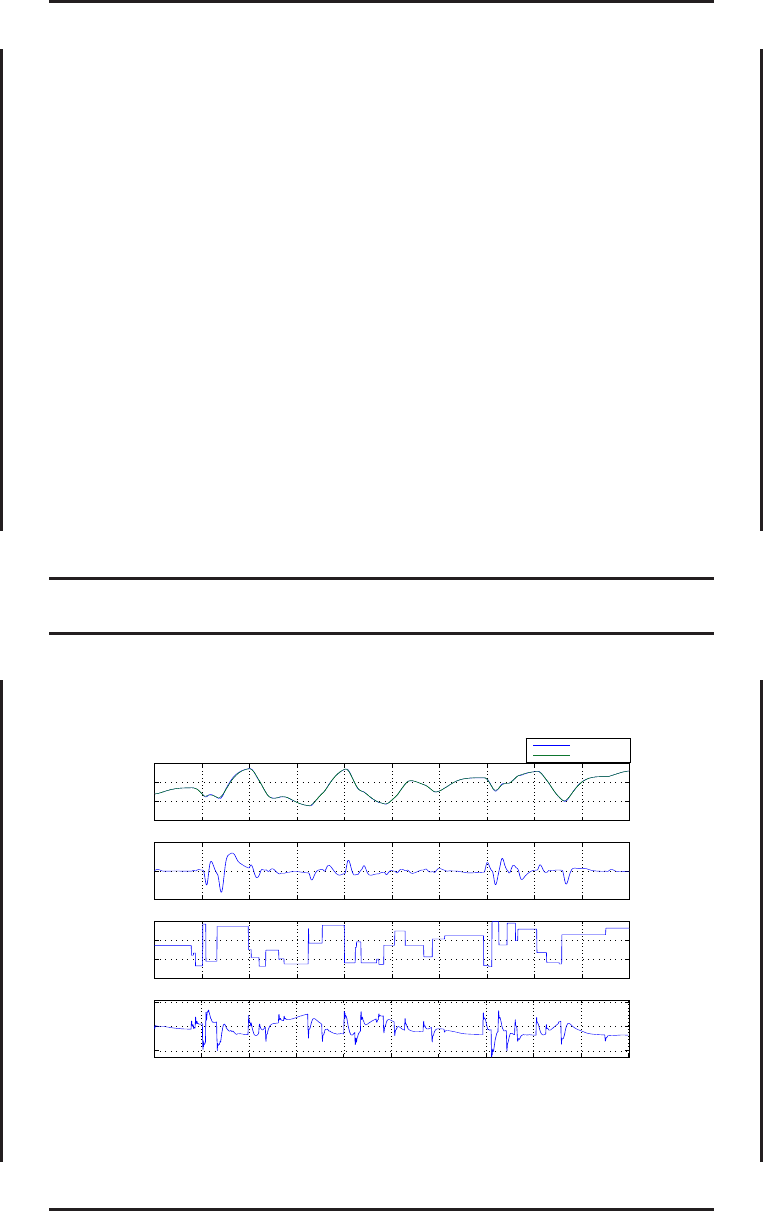
Результаты вычислительного эксперимента для системы управления с прогнозирующей

моделью и компенсатором, без отказов (ГЗЛА X-43, режим полета с числом Маха

M = 6). Обозначения: α — угол атаки, град.; e

— ошибка отслеживания заданного угла

атаки, град.; α

ref

— задающий сигна л по углу атаки, град.; φ

act

— командный сигнал для

привода элевонов, град.; t — время, с; Plant — объе кт управления; RefModel — эталонная

модель.

Ю. В. Тюменцев 178

Оптимальное управление

Slide 357

Адаптивное управление с ПМ (IX)

Вычислительный эксперимент для управления с ПМ – 2

0 10 20 30 40 50 60 70 80 90 100

α, deg

failures: dXt=+5% (t=30s), dmzfi=−30% (t=60s)

10 20 30 40 50 60 70 80 90 100

, deg

0 10 20 30 40 50 60 70 80 90 100

−5

ref

, deg

0 10 20 30 40 50 60 70 80 90 100

−10

act

, deg

t, sec

Plant

RefModel

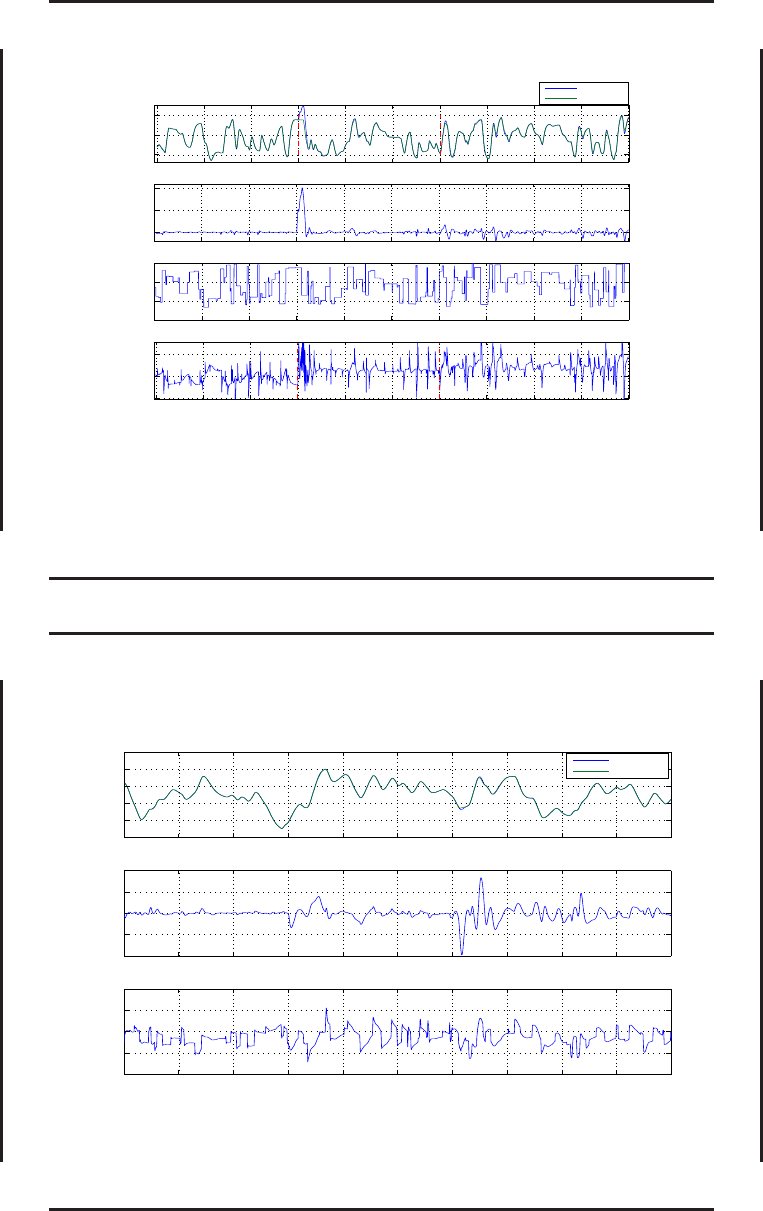
Результаты вычислительного эксперимента для системы управления с прогнозирующей

моделью и компенсатором (ГЗЛА X-43, режим полета с числом Маха M = 6). Адаптация

к изменению динамики объекта управления вследствие отказов: смещение центровки н а

5% назад ( t = 30 с), 30% уменьшение эффективности органа управления (t = 60 с).

Обозначения: α — угол атаки, град.; e

— ошибка отслеживания заданного угла атаки,

град.; α

ref

— задающий сигна л по углу атаки, град.; φ

act

— командный сигнал для

привода элевонов, град.; t — время, с; Plant — объе кт управления; RefModel — эталонная

модель.

Slide 358

Адаптивное управление с ПМ (X)

Вычислительный эксперимент для управления с ПМ – 3

0 10 20 30 40 50 60 70 80 90 100

−20

−10

α, deg

dXt=+0.05 at t=30s, dMzfi−50% at t=60s, online ident training

0 10 20 30 40 50 60 70 80 90 100

−1

−0.5

0.5

∆α, deg

0 10 20 30 40 50 60 70 80 90 100

−20

−10

φ, deg

t, sec

Object

RefModel

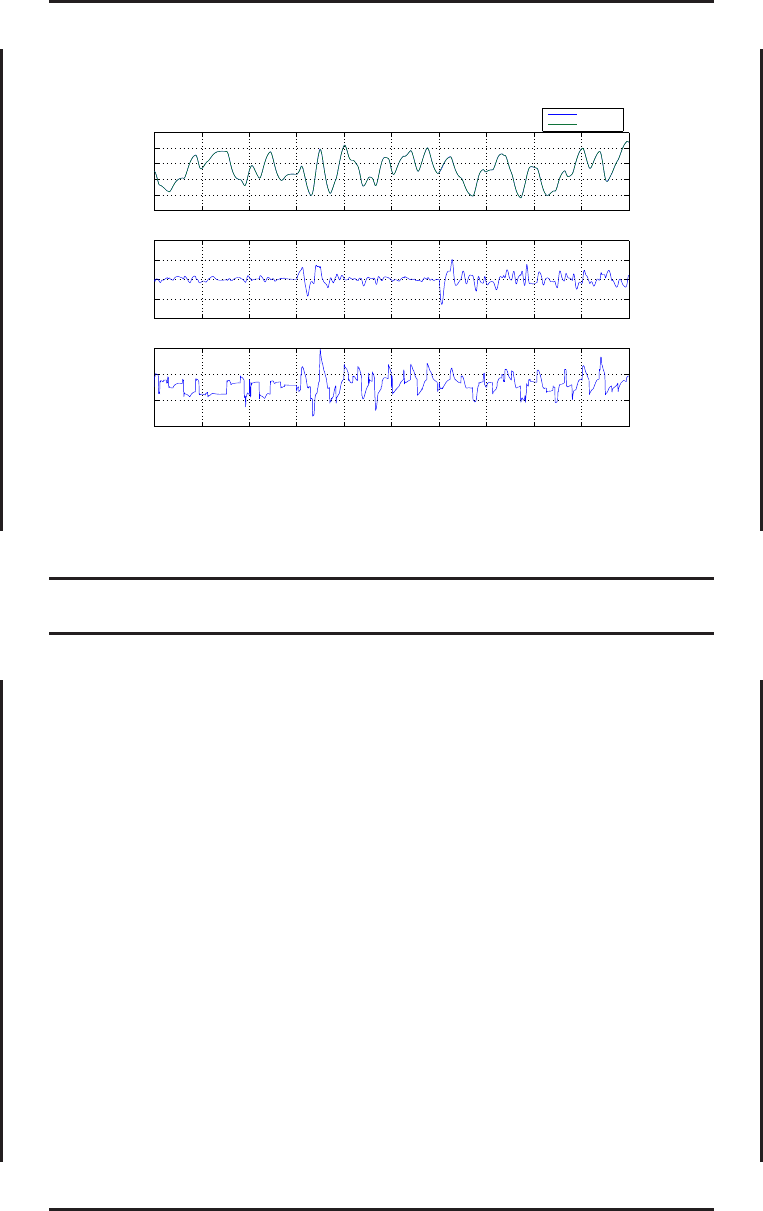
Результаты вычислительного эксперимента для системы управления с прогнозирующей

моделью и компенсатором (самолет F-16, режим полета с индикаторной скоростью

ind

= 300 к м/ч). Обозначения: α — угол атаки, град.; e

— ошибка отслеживания

заданного угла атаки, град.; α

ref

— задающий сигна л по углу атаки, град.; φ

act

—

командный сигнал для привода элевонов, град.; t — время, с; Plant — объе к т управления;

RefModel — э талонная модель.

Ю. В. Тюменцев 179

Оптимальное управление

Slide 359

Адаптивное управление с ПМ (XI)

Вычислительный эксперимент для управления с ПМ – 4

0 10 20 30 40 50 60 70 80 90 100

−20

−10

α, deg

dXt=+0.05 at t=30s, dMzfi−50% at t=60s, online ident training

0 10 20 30 40 50 60 70 80 90 100

−1

−0.5

0.5

∆α, deg

0 10 20 30 40 50 60 70 80 90 100

−20

−10

φ, deg

t, sec

Object

RefModel

Результаты вычислительного эксперимента для системы управления с прогнозирующей

моделью и компенсатором (самолет F-16, режим полета с индикаторной скоростью

ind

= 500 к м/ч). Обозначения: α — угол атаки, град.; e

— ошибка отслеживания

заданного угла атаки, град.; α

ref

— задающий сигна л по углу атаки, град.; φ

act

—

командный сигнал для привода элевонов, град.; t — время, с; Plant — объе к т управления;

RefModel — э талонная модель.

Slide 360

Адаптивное управление с ПМ (XII)

Вычислительный эксперимент для управления с ПМ – 5

Поведение ЛА под управлением системы с прогнозирующей моделью в

значительной степени подобно его поведению под управлением системы с

эталонной моделью.

Выводы, которые следуют из результатов вычислительных экспериментов для

схемы с ПМ, в целом аналогичны тем, что были сделаны для систем с эталонной

моделью.

А именно, в подавляющем большинстве случаев адаптивная нейросетевая

система у правления с ПМ успешно справляется со своими задача ми, в том числе

и при возникновении отк азных ситуаций.

Сопоставление схем адаптивного управления с эталонной моделью и с

прогнозирующей моделью не позволяет отдать предпочтение ни одной из них.

У каждой из них есть свои полож ительные и отрицательные свойства.

Окончательное решение в пользу какой-либо одной из этих схем можно сделать

лишь применительно к конкретной решаемой прикладной задач е, после

проведения достаточно обширной серии вычислительных экспериментов.

Ю. В. Тюменцев 180