Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 361

Адаптивное управление с ИМ (I)

Расширение состава схем адаптивного управления

Ранее были введены в рассмотрение две схемы адаптивного управления (схема с

эталонной моделью (ЭМ) и схема с прогнозирующей моделью (ПМ)), которые

оценивались с точки зрения их использования для управления движением ЛА.

Как показал проведенный анализ, возможностей этих двух классов систем

адаптивного управления не всегда достаточно для решения рассматриваемых

задач управления движением ЛА с требуемым качеством.

Наряду с дальнейшим совершенствованием схем с ЭМ и ПМ, осуществляемой за

счет привлечения более мощных средств НС-моделирования, представляется

целесообразным также расширить перечень рассматриваемых схем адаптивного

управления.

Один из очевидных кандидатов на включение в такой расширенный перечень —

это схема с инверсно й моделью (ИМ).

Схему управления с ИМ можно представить в двух вариантах: неадаптивном и

адаптивном, точно так же, как это имеет место и для схем управления с ЭМ и

ПМ.

Slide 362

Адаптивное управление с ИМ (II)

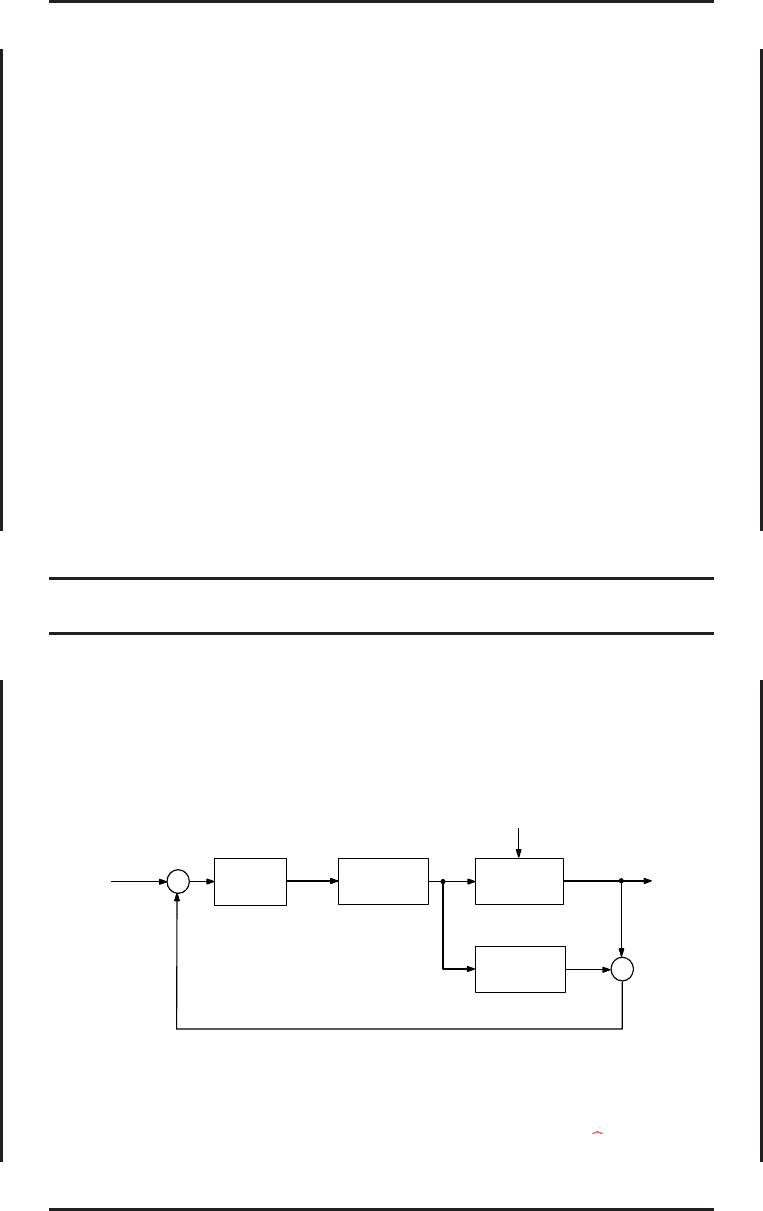
Неадаптивная схема управления с ИМ – 1

Неадаптивная схема управл ения с ИМ, известная в теории управления как система с

косвенным измерением возмущений, исследовалась на устойчивость и робастность при

управлении нелинейными объектами и продемонстрировала возможность достижения

высокого качества управления.

Объект

управления

−

Инверсная

НС-модель

объекта

Прямая

НС-модель

объекта

Фильтр

g(t)

u(t)

y(t)

(t)

r(t)

ξ(t)

u(t)

−

Структурная схема системы управления с прямой и инверсной

НС-моделями объекта управления

Здесь: r(t) — задающее воздействие; ξ(t) — возмущающе е воздействие; g(t) — сигнал на

выходе фильтра; u(t) — управлени е; y(t) — выход объекта управления; y(t) — выход

нейросетевой модели объекта управления; ε

(t) — расхождение между выходами объекта

управления и НС-модели.

Ю. В. Тюменцев 181

Оптимальное управление

Slide 363

Адаптивное управление с ИМ (II)

Неадаптивная схема управления с ИМ – 2

Помимо инверсной НС-модели, в состав систем управ ления с ИМ входит также и прямая

НС-модель объекта управления (э то точно такая же модель объекта, которая входила в

состав систем управле ния с ЭМ и ПМ).

При соответствующем выборе операторов для элементов системы (т.е. фильтра, прямой и

инверсной модели) выходная переменная y(t) воспроизводит входной (задающий) сигнал

g(t) с желаемой динамикой и не зависит от возмущени й ξ(t), приведенных к выходу

объекта управления.

Это возможно, если инверсная модель объекта управления реализует инверсный оператор

−1

, а прямая модель — прямой оператор A объекта управления.

Для достижен ия желаемой динамики системы в ее состав вводится фильтр, реализующий

оператор вида

= A

−1

A ,

где A

−1

— реализация инверсной моделью точного инверсного оператора A

−1

; A —

реализация прямой моделью точного прямого оператора A. В этом случае сигнал r(t)

воспроизводится на выходе объекта без искажений, т.е. y(t) ≡ r(t) и не зависит от

возмущения ζ(t), эквивалентного возмущению ξ(t) и приведенного ко входу объекта.

Slide 364

Адаптивное управление с ИМ (III)

Неадаптивная схема управления с ИМ – 3

Если прямая и инверсная модели объе к та управления реализованы точно, т.е. если

−1

= A

−1

и A = A,

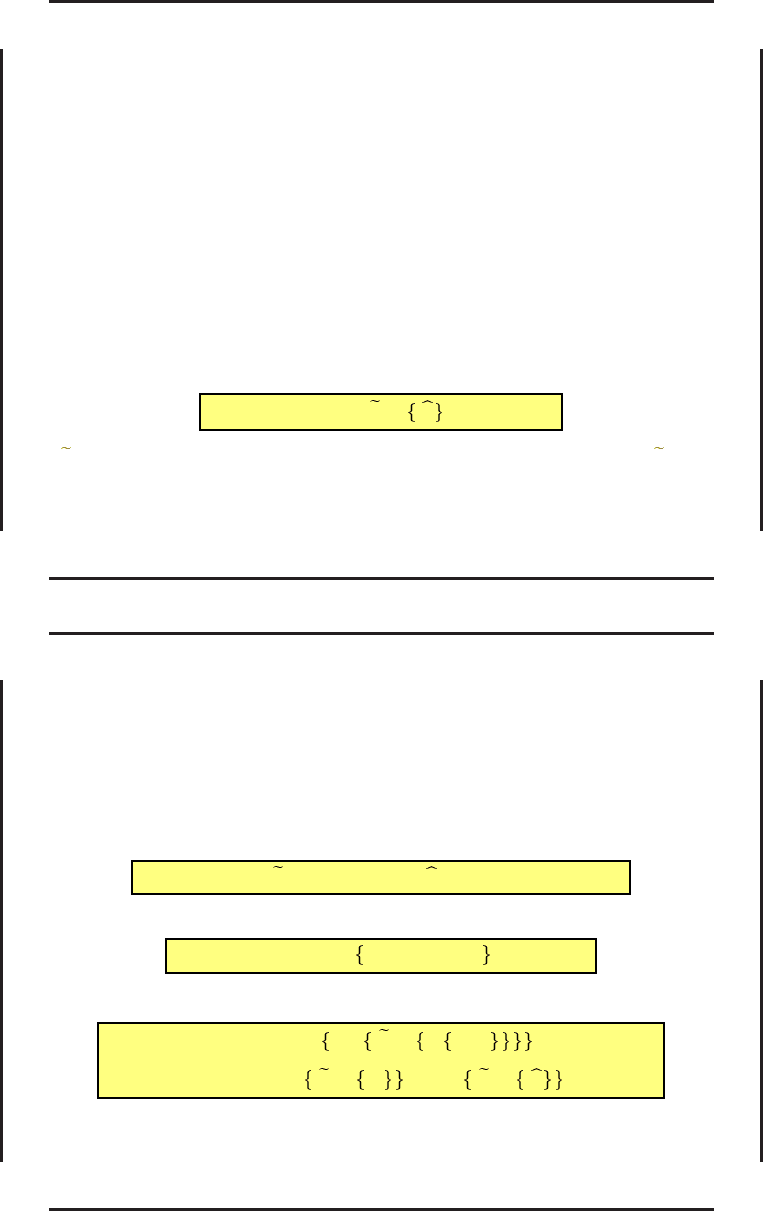
тогда

y(t) = A

r(t) − ε

(t) .

Вход и выход системы в рассматриваемом случае связаны операторным соотношением

y(t) = L

−1

A r(t) ,

L = 1 + A

−1

A − A

−1

Ю. В. Тюменцев 182

Оптимальное управление

Slide 365

Адаптивное управление с ИМ (IV)

Неадаптивная схема управления с ИМ – 4

В неадаптивной системе управления с ИМ рассмотренного вида могут возникать

проблемы устойчивости и робастности из-за недостаточно точной реализации

прямой и ин версной моделей объекта управления.

Если объект управления нелинейный и мно госвязный по своей природе, к ак это

и имеет место в случае маневренного самолета или ГЗЛА, аналитическое решение

проблемы едва ли возможно, остается лишь путь вычислительного

моделирования.

Как показывает имеющийся опыт, по-настоящему эффективную реализацию

прямой и ин версной моделей, пригодных по уровню достижимой ими точности к

использованию в составе систем управления с ИМ, обеспечивает лишь

нейросетевое моделирование или же нейронечеткое моделирование, когда

аппарат искусственных нейронных сетей используется совместно с аппаратом

нечеткой логики.

Slide 366

Адаптивное управление с ИМ (V)

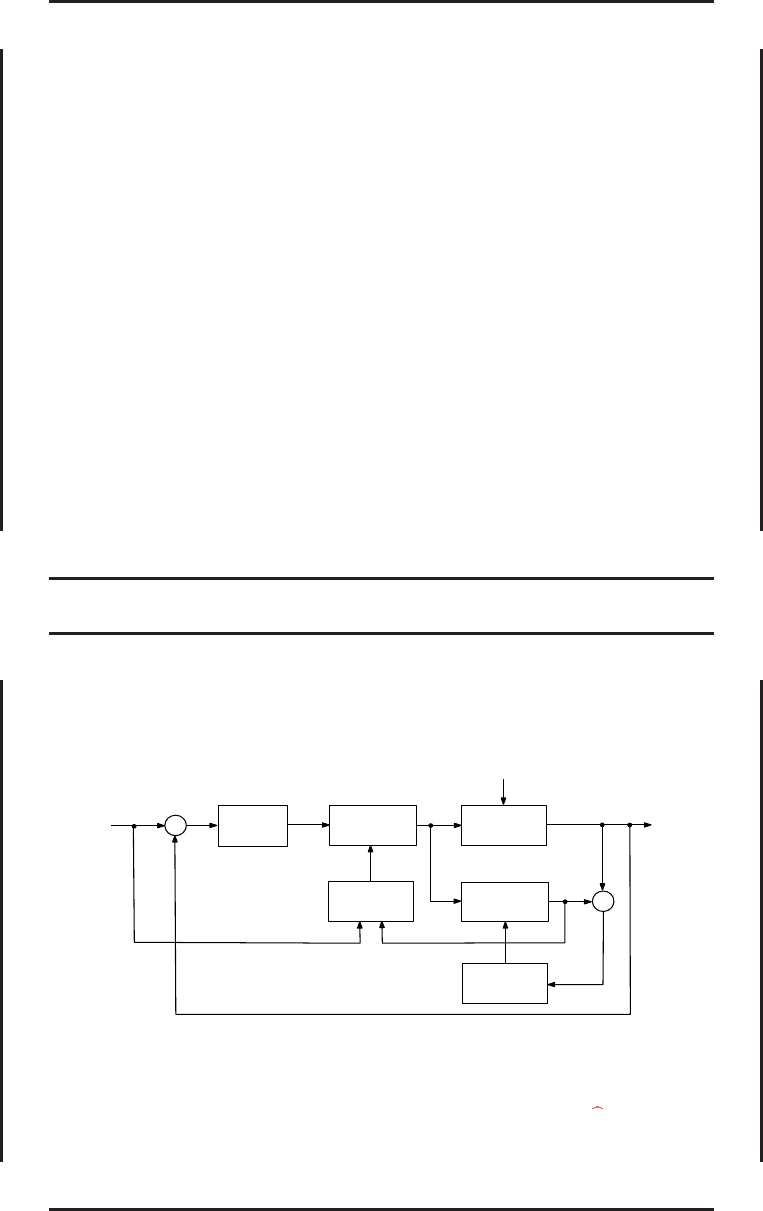
Адаптивная схема управления с ИМ – 1

Возможности неадаптивной системы управления с ИМ ограничиваются отс утствием

обратных связей по воспроизводимой функции r(t). Этого недостатка лишен адаптивный

вариант схемы с ИМ.

Объект

управления

−

Инверсная

НС-модель

объекта

Прямая

НС-модель

объекта

Фильтр

g(t)

u(t)

y(t)

(t)

r(t)

ξ(t)

u(t)

−

Алгоритм

обучения

Алгоритм

обучения

inv

dir

ε(t)

r(t)

y(t)

Структурная схема адаптивной системы управления с прямой и ин версной

НС-моделями объекта управления

Здесь: r(t) — задающее воздействие; ξ(t) — возмущающе е воздействие; g(t) — сигнал на

выходе фильтра; u(t) — управлени е; y(t) — выход объекта управления; y(t) — выход

нейросетевой модели объекта управления; ε

(t) — расхождение между выходами объекта

управления и НС-модели; ε(t) — расхождение между выходами объекта управления и

задающим воздействие; θ

dir

и θ

inv

— параметры прямой и инверсной модели объекта

управления, соответственно.

Ю. В. Тюменцев 183

Оптимальное управление

Slide 367

Адаптивное управление с ИМ (VI)

Адаптивная схема управления с ИМ – 2

Адаптивная система управления, построенная по схеме с И М, включает две

динамически настраиваемые модели, прямую и инверсную.

По указанным ранее причинам обе эти модели наиболее целесообразно

реализовывать в классе динамически обучаемых НС-моделей.

В алгоритме обучения инверсной модели используются текущие измерения

воспроизводимой (задающей) функции r(t) и выхода прямой модели объекта

y(t).

Прямая модель выполняется также в виде динамической сети, обучаемой по

прогнозу ошибки ε

(t).

Slide 368

Адаптивное управление с ИМ (VII)

Адаптивная схема управления с ИМ – 3

Предельные динамические свойства рассматриваемой системы вытекают из

следующих рассуждений. Для обучения прямой модели ошибка определяется

соотношением

(t) = y(t) − y(t) → 0, при t > 0,

так что y(t) → y(t).

При настройке инверсной модели используется ошибка обучения

(t) = g(t) − y(t) → 0, при t → ∞.

Следовательно,

y(t) → g(t) и y(t) → g(t).

Ю. В. Тюменцев 184

Оптимальное управление

Slide 369

Адаптивное управление с ИМ (VIII)

Адаптивная схема управления с ИМ – 4

Если A — оператор объекта управления, A

— оператор инверсной м одели, а

— оператор прямой модели, то цепочка предельных переходов при

обучении сетей

y(t) → y(t) → g(t) при t → ∞

осуществляется тогда, когда

= A

−1

= A

−1

В результате настройки, проведенной описываемым способом, получается

инверсная модель объекта управления, которая выполняет ф ункцию адаптивного

нейроконтроллера.

Адаптивность этой системы проявляется в том, что для ее структурного синтеза

требуется минимум априорной информации об объекте, кроме того, обе

модели, прямая и инверсная (т.е. нейроконтроллер), подстраиваются

непосредственно в процессе функционирования системы при неконтролируемых

изменениях динамики объекта управления.

Slide 370

Адаптивное управление с ИМ (IX)

Адаптивная схема управления с ИМ – 5

Проведенный анализ схемы адаптивного управления с инверсной моделью

показывает, что данная схема представляет безусловный интере с с точки зрения

задач управления движением ЛА, если удастся получить достаточно точные

модели объекта управления — прямую и, особенно, инверсную.

При этом следует учитывать, что динамика о бъекта может меняться резко и

непредсказуемо непосредственно в полете, в частности, из-за отказов

оборудования и повреждений конструкции.

Следовательно, необходимо располагать не только средствами построения

достаточно точных ИМ и ПМ на этапе структурного синтеза системы управления,

но и средствами оперативной корр е ктировки этих моделей непосредственно в

ходе полета.

Ю. В. Тюменцев 185