Тюменцев Ю.В. Оптимальное управление. Лекции-Слайды

Подождите немного. Документ загружается.

Оптимальное управление

Slide 301

Обучение нейросетевой модели движения ЛА

в режиме реального времени (I)

В используемых НС-моделях активационными функциями являются сигм оиды.

Такие глобальные активационные функции обладают хорошими обобщающими

свойствами. Однако при этом корректировка любого настраиваемого параметра

меняет поведение сети на всей области входных данных. Это значит, что при

попытке дообучения сети новым поступившим данным пропадут свойства сети на

предыдущих данных. Таким образом, чтобы принять в расчет поступающие

измерения, НС-модели рассматриваемого типа надо доучивать на очень большой

выборке, что неосуществимо с вычислительной точки зрения.

Для того, чтобы обойти эту проблему (использовать для обучения если не

текущее измерение, то хотя бы небольшой скользящий интервал), можно

использовать рекуррентный метод наименьших квадратов (РНМК).

Slide 302

Обучение нейросетевой модели движения ЛА

в режиме реального времени (II)

РМНК является частным случаем фильтра Калмана (ФК) при оценке постоянных

параметров. Однако ФК и РМНК напрямую применимы только для систем,

наблюдения которых линейны по оцениваемым парам етрам, а уравнение

наблюдения нейросети является нелинейным:

k+1

= w

+ v,

= f(x

, w

) + ǫ.

где v — шум объекта и ǫ— шум наблюдений, эти шумы являются гауссовскими

случайными последовательностями с нулевым средним, они характеризуются

матрицами корреляции M[v v

] = Q, M[ǫ ǫ

] = R, M[v ǫ

] = 0, под x

понимаются все входы в текущий момент.

Ю. В. Тюменцев 151

Оптимальное управление

Slide 303

Обучение нейросетевой модели движения ЛА

в режиме реального времени (III)

Для того, чтобы использовать ФК, нужно линеаризовать уравнение наблюдения.

Можно использовать статистическую линеаризаци ю, т. е. линеаризацию

относительно математического ожидания. Она дает:

k+1

= w

+ v,

= H

+ ǫ,

где матрица наблюдения имеет вид

∂y

∂w

w=w

x=x

= −

∂e

∂w

= −J

Slide 304

Обучение нейросетевой модели движения ЛА

в режиме реального времени (IV)

Уравнения фильтра Калмана для оценки w

k+1

на следующем шаге (не

обязательно на шаге дискретизации) выглядят следующим образом:

= H

+ R,

= P

−1

k+1

= P

− K

+ Q,

k+1

= w

+ K

здесь e

— вектор ошибки наблюдения на k-м шаге оценивания:

= y

− y

= y

− f(x

, w

а величина β — коэффициент забывания, влияет на значимость предыдущих

шагов. Если смотреть назад по шагам, эта значимость уменьшается по экспоненте

(если β = const).

Ю. В. Тюменцев 152

Оптимальное управление

Slide 305

Обучение нейросетевой модели движения ЛА

в режиме реального времени (V)

Таким образом видно, что опять ключевым моментом (особенно для динамических

сетей) является вычисление якобиана J

ошибок сети по на стра иваемым

параметрам.

Отличие только в способе оптимизации — ФК использует рекуррентную

процедуру. Если оценивать параметры, линейно связанные с наблюдениями, то

ФК обладает бесконечной памятью, т. е. действительно реализует рекуррентный

МНК (фактически нет различия между и спользованием МНК на всей выборке и

использованием на этой выборке ФК указанным выше способом).

Однако для нелинейной системы это уже не будет справедливым, поскольку J

вообще говоря является случайной величиной (зависит от конкретного состояния)

и могут получаться противоречивые направления на каждом ша ге оценивания.

Из-за этого, по-видимому, стирается информация в матрице ковариации P

предыдущих измерениях и в конце концов оценка расходится.

Slide 306

Обучение нейросетевой модели движения ЛА

в режиме реального времени (VI)

Поэтому при обучении нейросети использовать в ФК по одному поступающему измерению

нельзя — нужно делать оценку на интервале наблюдений, чтобы обновление матрицы P

происходило более корректно.

Можно в качестве вектора наблюдений взять не текущий выход сети, а последовательность

значений на некотором скользящем интервале наблюдения

= [y

i−l

, y

i−l+1

, . . . , y

]

где l — длина скользящего интервала, индекс i относится к моменту времени (шагу

дискретизации), а индекс k указывает номер оценки. Ошибка также будет векторной

величиной:

= [e

i−l

, e

i−l+1

, . . . , e

]

тогда якобиан будет не вектором, а матрицей. Если в текущий мом ент наблюдается вектор

, тогда вектор ошибки будет составным вектором из векторов ошибки в мом енты времени,

относящиеся к скользящему интервалу, якобиан станет блочным, а все уравнения ФК

останутся без изменения.

Для экономии времени оценка параметров производится не на каждом шаге дискретизации, а

прорежена в десять раз (дискретизация 0.01 с, а обновление параметров сети происходит

каждую 0.1 с). Вычислительный эксперимент показывает, что такое «огрубление» вполне

приемлемо, поскольку несущественно сказывается на точности модели.

Ю. В. Тюменцев 153

Оптимальное управление

Slide 307

Оценка работоспособности нейросетевой модели

движения ЛА на основе многослойной

нейронной сети (I)

Оценка работоспособности рассматриваемой НС-модели проводилось применительно к

угловому продольному движению летательного аппарата, которое описывалось с помощью

математической модели, традиционной для динамики полета самолетов:

˙α = ω

−

(α, ω

, ϕ) +

˙ω

qSb

(α, ω

, ϕ) ,

¨ϕ = −2T ζ ˙ϕ − ϕ + ϕ

act

(169)

где α — угол атаки, град; ω

— угловая скорость тангажа, град/с; ϕ — угол отклонения

управляемого стабилизатора, град; C

— коэффициент подъемной силы; m

—

коэффициент момента тангажа; m — масса самолета, кг; V — воздушная скорость, м/с;

q = ρV

/2 — скоростной напор; ρ — плотность воздуха, кг/м

; g — ускорение силы

тяжести, м/с

; S — площадь крыла, м

; b

— средняя аэродинамическая хорда крыла, м;

— момент инерции самолета относительно боковой оси, кг·м

; безразмерные

коэффициенты C

и m

являются нелинейными функциями своих аргументов; T, ζ —

постоянная времени и коэффициент относительного демпфирования привода, ϕ

act

—

командный сигнал на привод (ограничивается ±25

◦

В модели (169) величины α, ω

, ϕ и ˙ϕ — это состояния объекта управления, величина ϕ

act

— управление.

Slide 308

Оценка работоспособности нейросетевой модели

движения ЛА на основе многослойной

нейронной сети (II)

10 20 30 40 50 60 70 80 90 100

−20

α, deg

Training data for NN plant model

10 20 30 40 50 60 70 80 90 100

−30

−20

−10

act

, deg

t, sec

Формирование нейросетевой модели объекта управления ( самолет F-16, режим полета

с индикаторной скоростью V

= 500 км/ч) — обучающая выборка для НС-модели

Здесь: α — угол атаки, град.; φ

act

— командный сигнал привода органа управления;

t — время, с

Ю. В. Тюменцев 154

Оптимальное управление

Slide 309

Оценка работоспособности нейросетевой модели

движения ЛА на основе многослойной

нейронной сети (III)

Для формирования обучающих выборок реализуется очень активная раб ота

органом управления продольным движением (управляемый стабилизатор для

F-16), выражающаяся в частом изменении зн ачения командного сигнала φ

act

привода органа управления при существенных перепадах между соседними

значениями (этот командный сигнал формировался случайным образом).

Цель применения такого способа формирования обучающего набора состоит в

том, чтобы обеспечить возможно большее разнообразие состояний моделируемой

системы (чтобы покрыть по-возможности равномерно и плотно все пространство

состояний системы), а также возможно большее разнообразие перепадов

соседних по времени состояний (чтобы максимально достоверно отразить в

НС-модели динамику моделируемой системы).

Slide 310

Оценка работоспособности нейросетевой модели

движения ЛА на основе многослойной

нейронной сети (IV)

Поскольку целью у правления в рассматриваемой задаче является максимально

точное отслеживание требуемых зн ачений угла атаки, то, соответственно, оценка

точности формируемой модели осуществляется сопоставлением поведения по этой

величине для исходного объекта управления, описываемого системой

дифференциальных уравнений (169) и сформированной НС-модели. Точность

модели оценивается ошибкой e

, вычисляемой как разность углов атаки для

объекта управления и НС-модели в один и тот же момент времени.

Из примера на следующем слайде видно, что предлагаемый подход дает

возможность строить довольно точные НС-модели (значение ∆α в пределах

±(0.5 ÷ 0.7 град.), однако в ряде случ аев точность ухудшается, что

впоследствии является причиной получения неудовлетворительных адаптационных

свойств синтезированных нейроконтроллеров. Некоторые пути преодоления этих

затруднений рассматриваются далее.

Ю. В. Тюменцев 155

Оптимальное управление

Slide 311

Оценка работоспособности нейросетевой модели

движения ЛА на основе многослойной

нейронной сети (V)

0 10 20 30 40 50 60 70 80 90 100

−20

−10

α, deg

Target

Inet output

0 10 20 30 40 50 60 70 80 90 100

−3

−2

−1

∆α, deg

t, sec

error

Формирование нейросетевой модели объекта управления ( самолет F-16, режим полета

с индикаторной скоростью V

= 500 к м/ч) — проверка работоспособности замкнутой

НС-модели

Здесь: α — угол атаки, град.; ∆α — ошибка (расхождение углов атаки для объекта и

НС-модели), град.; t — время, с; Target — выход объекта; Inet output — выход НС-модели;

Error — ошибка отслеживания

Slide 312

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (I)

Проблема адаптивного управления – 1

Существует значительное число схем адаптивного управления, в том числе и в нейросетевом

исполнении.

К числу наиболее популярных из них можно отнести адаптивное управление с эталонной

моделью, а также адаптивное управлени е с прогнозирующей моделью. Как уже отмечалось,

традиционная теория управления требует знания математической модели объекта, входящих в

эту модель параметров и характеристик объекта, а также параметров и характеристик среды,

в которой данный объект функци он ирует.

На практике эти требования далеко не всегда могу т быть удовлетворены. Кром е того, в

процессе функциониров ания параметры и характеристики объекта и среды могут значительно

изменяться. В этих случаях традиционные методы часто дают неудовлетворительные

результаты.

В связи с этим возникает потребность в построении управляющих систем, не требующих

полного априорного знания объе кта управления и условий его функционирования. Такая

система должна быть в состоянии приспосабливаться к меняющимся свойствам и условиям

функционирования объекта. Этим требованиям отвечают адаптивные системы, в которых

текущая доступная информация и спользуется не только для выработки управ ляющего

воздействия (как в обычных неадаптивных системах), но также и для изменения

(корректировки) алгоритма упра вления.

Ю. В. Тюменцев 156

Оптимальное управление

Slide 313

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (II)

Проблема адаптивного управления – 2

Принято выделять два основных класса адаптивных систем:

❑ самонастраивающиеся системы, в которых в ходе работы структура

алгоритма управления не меняется, а изменяются только его параметры;

❑ самоорганизующиеся системы, в которых в ходе работы изменяется

структура алгоритма управления.

Slide 314

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (III)

Проблема адаптивного управления – 3

Помимо того, что адаптивные системы обеспечивают принципиальную

возможность управления объектом в условиях неопределенности, они позволяют

получить также еще ряд важных для практики результатов, в том числе:

❑ обеспечить оптимальный режим работы системы управления в условиях

неполной информаци и , если в формулировку цели для системы входит

оптимизирующий функционал;

❑ обеспечить работоспособность системы управления в условиях изменения

динамических свойств объекта в широких пределах;

❑ создать унифицированные регуляторы для широкого класса объектов и

заменить при этом перенастройку параметров обычного регулятора на

механизмы адаптации, осуществляющие эту перенастройку при смене

объекта;

❑ снизить технологические требования (точность и т. п.) к узлам и элементам

объекта управления;

❑ сократить сроки разработки и наладки систем за счет использования

типовых решений с их последующей адаптацией.

Ю. В. Тюменцев 157

Оптимальное управление

Slide 315

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (IV)

Основные структурные варианты адаптивных систем – 1

Как уже отмечалось, система управления считается адаптивной, если в ней

текущая информация о состоянии системы и спользуется не только для выработки

управляющего воздействия (ка к это имеет место в обычных, неадаптивных,

системах), но также и для изменения (корректировки) алгоритма управления.

В общем виде в адаптивной системе корректирующее воздействие ξ(t) для

регулятора вырабатывается с помощью механизма адаптации, использующего в

качестве входной информации значения управления u(t), выхода объекта y(t), а

также дополнительную информацию «внешнего» характера ψ(λ), λ ∈ Λ,

которую следует учитывать при выработке корректирующего воздействия

(например, скорость и высота полета летательного аппарата в задаче управления

его угловым движением).

Slide 316

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (V)

Основные структурные варианты адаптивных систем – 2

Объект

управления

Регулятор

Механизм

адаптации

r(t)

y(t)

u(t)

ξ(t)

ψ(λ)

Схема управляемой системы с подстраиваемым законом управления, реализуемым

регулятором

Здесь: r(t) — задающее воздействие; u(t) — управление; y(t) — выход объекта

управления; ξ(t) — корректирующее воздействие для регулятора; ψ(λ), λ ∈ Λ —

дополнительная информация, которую следует учитывать при выр аботке корректирующего

воздействия (н апример, скорость и высота полета летательного аппарата в задаче управления

его угловым движением)

Ю. В. Тюменцев 158

Оптимальное управление

Slide 317

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (VI)

Основные структурные варианты адаптивных систем – 3

Возможны различные частные варианты общей схемы, отличающиеся друг от

друга составом входной информации, используемой при выработке

корректирующего воздействия ξ(t).

Один из таких вариантов состоит в том, что корректировка осуществляется только

на основе «внешней» информации ψ(λ), λ ∈ Λ; он именуется

программированием коэффициентов регулятора (GS — Gain Scheduling в

англоязычной литературе).

Принципиальное отличие GS-подхода от полного варианта адаптационной схемы

состоит в том, что в GS-подходе значения корректирующих воздействий ξ как

функция от ψ(λ) должны быть вычислены зара нее (off-line), после чего данная

функция используется в неизменном виде в процессе управления объектом.

В полном варианте адаптационной схемы алгоритм корректировки перестает быть

неизменным, он уточняется непосредственно (on-line) в ходе работы системы.

Несмотря на ограниченные адаптационные возможности GS-подхода, он довольно

часто используется на практике.

Slide 318

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (VII)

Основные структурные варианты адаптивных систем – 4

Объект

управления

r(t)

y(t)

u(t)

ξ(t)

ψ(λ)

Регулятор

Механизм

адаптации

Схема корректиров к и параметров закона управления, реализуемого регулятором по схеме

с программированием его коэффициентов (GS — Gain Scheduling)

Здесь: r(t) — задающее воздействие; u(t) — управление; y(t) — выход объекта

управления; ξ(t) — корректирующее воздействие для регулятора; ψ(λ), λ ∈ Λ —

информация, на основании которой осуществляется выра ботка корректирующего воздействия

Ю. В. Тюменцев 159

Оптимальное управление

Slide 319

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (VIII)

Основные структурные варианты адаптивных систем – 5

Схемы адаптивного управления принято разделять на два основных вида: прямое

адаптивное управление и непрямое адаптивное управление.

Схемы прямого адаптивного управления часто основываются на использовании

некоторой эталонной модели (ЭМ), задающей требуемый характер поведения

рассматриваемой системы.

В системах прямого адаптивного управления параметры регулятора θ

(t)

корректируются по алгоритму, реализуемому законом адаптации, который

вычисляет значения производной

(t) или разности θ

(t + 1) − θ

(t).

Это вычисление основывается непосредственно на значении ошибки слежения

ε(t) = y(t) − y

(t).

Slide 320

Схемы адаптивного управления, перспективные с

точки зрения задач управления полетом ЛА —

общая характеристика (IX)

Основные структурные варианты адаптивных систем – 6

r(t)

y(t)

u(t)

Регулятор

Ψ(r, y, θ

)

Объект

F(u, y)

(t)

u(t)

Закон

адаптации

(t))

Эталонная

модель

ε(t)

y(t)

−

r(t)

(t)

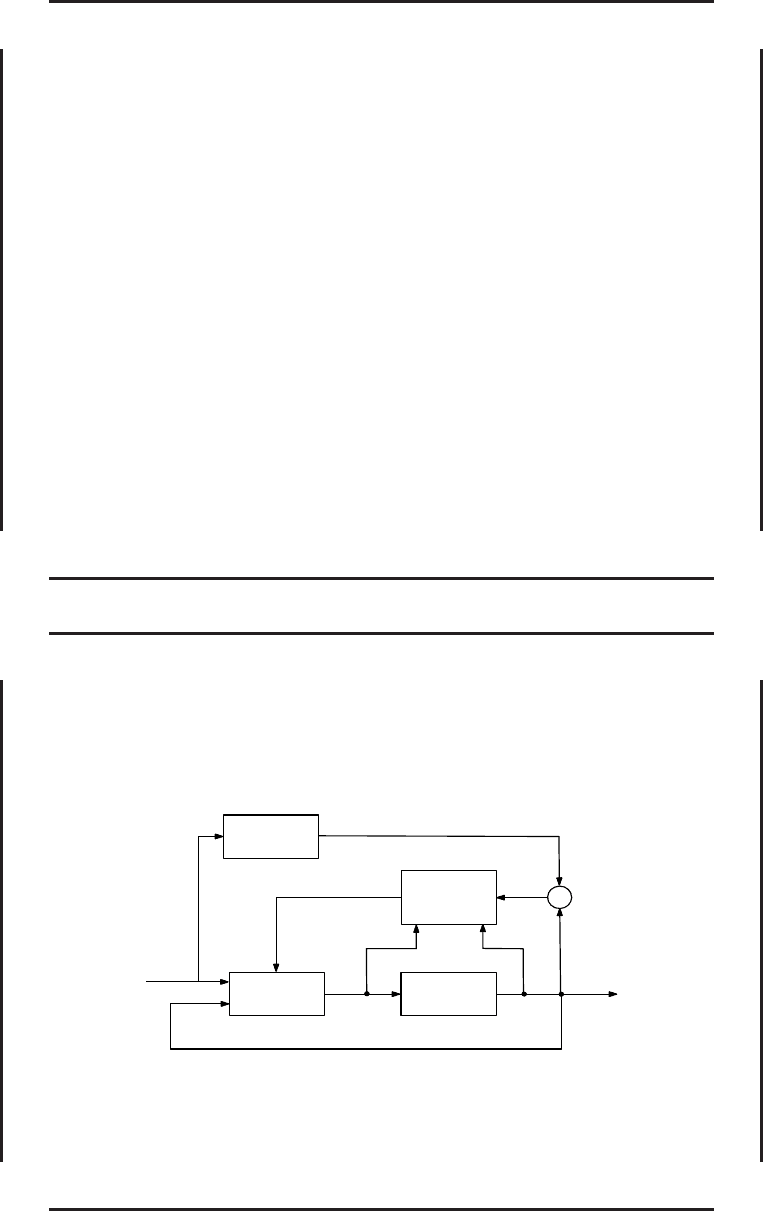
Прямая схема адаптивного у правления

Здесь: r(t) — задающее воздействие; u(t) — управление; y(t) — выход

объекта управления; y

(t) — выход эталонной модели; θ

(t) — корректируемые

параметры регулятора; ε(t) = y(t) − y

(t) — расхождение между выходами

объекта и эталонной модели.

Ю. В. Тюменцев 160