Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

630
14.7.7. По заону преломления = n. Если sin β =, де
n
1
— поазатель преломления воды, то произойдет полное внутрен-
нее отражение от поверхности раздела стело—вода. Тода sin α =
= n sin β = n
1
= 1,33, т. е. условия задачи неосуществимы.
О т в е т: таоо ула нет.
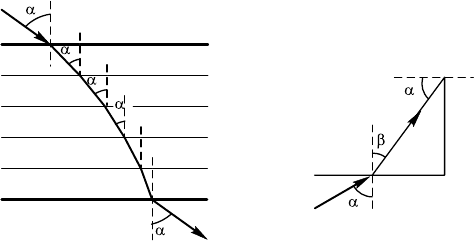
14.7.8. Разобьем всю пластину на N достаточно тоних слоев,
таих, что в пределах аждоо слоя поазатель преломления мож-
но считать неизменным, а луч — прямолинейным (рис. 14.7.5).
Заоны преломления на раницах слоев имеют вид:
=, =, =, …, = ,
де (N + 1)-й слой лежит уже за пределами пластины, т. е. α
N+1
—
это уол, под оторым луч выходит из пластины, а n
N+1
= n. Пере-
множая вышеприведенные равенства, получаем
===1,
отуда следует, что α
N+1
= α. Таим образом, вышедший из пласти-
ны луч будет параллелен лучу, падающему на пластину.
О т в е т: α
N + 1
= α.
14.7.10. Проследим ход произвольноо луча. Луч падает на
рань CD под уломα
1
, преломляется под улом β
1
и попадает на
рань ED под улом α
2
(рис. 14.7.6).
Для тоо чтобы луч вышел из стела, необходимо, чтобы уол паде-
ния α
2
был меньше предельноо ула полноо внутреннео отражения
для раницы стело—воздух: α
2
< α
n
.
αsin
βsin
------------ -
n
1
n
------
αsin
α
1
sin
----------------
n
1
n
------
α
1
sin
α
2
sin
----------------
n
2
n
1
------
α
2
sin
α
3
sin
----------------
n
3
n
2
------
α
N
sin
α
N 1+
sin
----------------------- -
n
N 1+
n
N
---------------
αsin
α
N 1+
sin
----------------------- -
n
N 1+
n
---------------
n
n
---
1
2
3
N+
1
n
1
n
n
2
n
3
n
N
n
N+1
=n
x
= n
Рис. 14.7.5
1
1
2
D
E
A
C
Рис. 14.7.6
631
По заону преломления n
с
sin α
n
= n
воз
sin 90° (n
воз
=1), отуда
sin α
n
=.
Следовательно,
sin α
2
<. (1)
Для раницы воздух — стело запишем заон преломления:
n
воз
sin α
1
= n
с
sin β
1
,(2)
отуда
sin β
1
= . (3)
Та а α
2
=90° – β
1
, то
sin α
2
=cosβ, (4)
cos β
1
=. (5)
Решив систему уравнений (1)—(5), получим
sin
2
α
1
> –1.
Подставив значение поазателя преломления n
с
= 1,5, получим
sin
2
α
1
>1,25.
Данное неравенство не имеет решения. Поэтому ни один луч,
попавший на нижнюю рань CD, не выйдет через боовую рань ED
убиа.
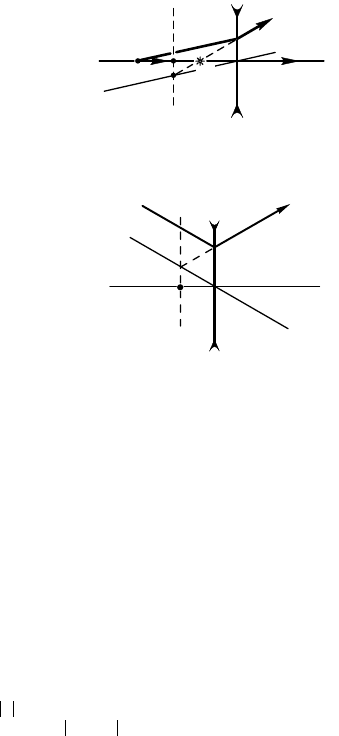
14.8.4. Полное внутреннее отраже-
ние выходящео луча наступит при β
2
=
=90° (рис. 14.8.8). Соласно заону пре-
ломления sin β
2
= n sin α
2
или n sin α
2
= 1,
отуда
α
2
= arcsin = 41,8°.
Посольу сумма улов 45°, 90° – β
1
и90° – β
2
треуольниа ABC
равна 180°, найдем β
1
=45° – β
2
=3,2°. Далее имеем sin α
1
= n sin β
1
,
отуда α
1
=arcsin (n sin β
1
) = 4,7°.
О т в е т: α
1
= 4,7°.
1
n
с
------
1
n
c
------
α
1
sin
n
----------------
1 sin
2
β
1
−
n
с
2
1
1
2
i
2
A
B
C
Рис. 14.8.8
1
n
---

632
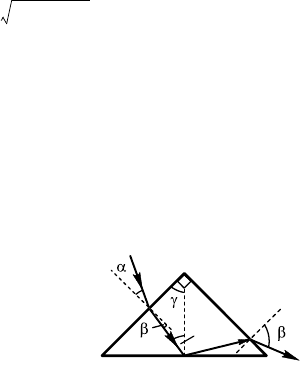
14.8.8. Для тоо чтобы свет вышел в
воду через рань AC, необходимо, чтобы
на ранице BC произошло полное внутрен-
нее отражение. При этом α
2
l α
n
(уол па-
дения больше или равен предельному у-
лу), а уол падения на рань AC α
3
был
меньше предельноо ула полноо внут-
реннео отражения. Построим ход луча
(рис. 14.8.9). Учтем, что β = α
2
или β = α
n
.
Для нахождения предельноо ула за-
пишем заон преломления. Для случая
полноо отражения
n
ст
sin α
n
= n
в
sin 90°,
де n
в
= 1,3 — поазатель преломления воды, n
ст
= 1,5 — поазатель
преломления стела. Из последнео равенства имеем
sin α
n
=, α
n
= arcsin , α
n
=62,5°, β l 62,5°.
Для тоо чтобы луч дости рани AC, уол призмы β должен быть
больше или равен 62,5°.
Для тоо чтобы свет вышел через рань AC, уол падения α
3
дол-
жен быть меньше предельноо, т. е. α
3
< 62,5°. Из рисуна находим
∠ AMN = ∠1+∠3,
90° – α
3
=2(90° – β) ^ 2β =90° + α
3
^ β <76,2°.
Таим образом, для тоо чтобы свет вышел через рань AC, уол β
должен удовлетворять условию:
62,5° m β < 76,2°.
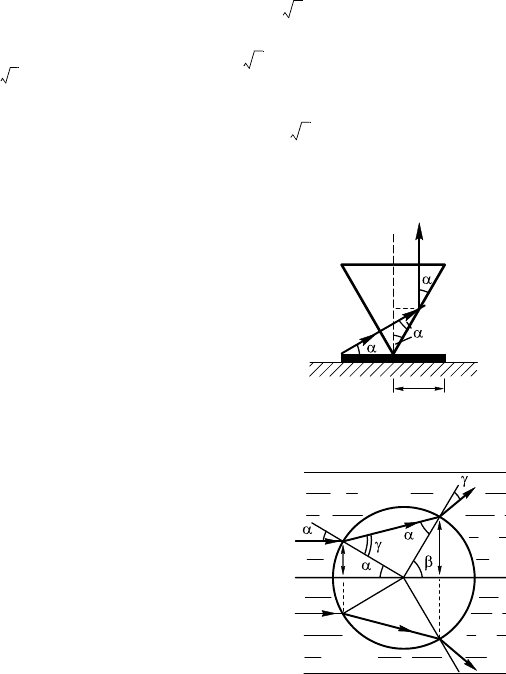
14.8.11. На чертеже (рис. 14.8.10)
поажем осевое сечение. Сначала рас-
смотрим ход одноо из лучей. На пер-
вой ранице свет не изменит направле-
ние распространения. Выясним, что
произойдет при падении света на боо-
вую поверхность онуса. Построим
уол падения α = 60°.
Вычислим предельный уол пол-
ноо отражения:
sin α
n
=,α
n
= arcsin , α
n
=42°.
3
2
1
2
3
N
M
A
C
B
Рис. 14.8.9
n
в
n
ст
------- -
1,3
1,5
---------
Рис. 14.8.10
1
r
1
r
2
d
A
1
2
30°
60°
B
2
1
n
---
1
n
---
633
В точе A произойдет полное отражение, та а α > α
n
. Отра-
женный луч попадает в точу B и выходит в воздух, не меняя на-
правления. Та а все падающие лучи от 1 до 2 параллельны меж-
ду собой, то и все преломленные лучи параллельны.
Все лучи, расположенные ниже оси онуса, после преломления
отлоняются вверх на таой же уол. Тода освещенная область
имеет вид ольца с внешним радиусом r
2
и внутренним r
1
.
Лучи, вышедшие через боовую поверхность онуса, составля-
ют уол 30° с вертиалью, поэтому r
1
= α .
Расстояние от центра равностороннео треуольниа до эрана Э
l = d + , поэтому r
2
= l ctg 30° = d +2R.
Находим площадь освещенноо ольца:
S = π –=πR 3R +4d d 126 см
2
.
14.8.12. Та а наблюдатель находится далео от онуса,
то лучи нему должны приходить параллельными. А это воз-
можно, если луч от рая монеты бу-
дет идти та, а поазано на ри-
суне 14.8.11. Следовательно, r =
=OB· sin α.
Треуольни SBO — равнобедрен-
ный, поэтому SO = OB = R. Площадь
изображения монеты S
1
= πr
2
= πR
2
sin
2
α.
Площадь монеты S
2
= πR
2
. Находим от-
ношение площадей
η = = =4.
О т в е т: площадь изображения мо-
неты меньше площади монеты в η =4
раза.
14.9.5. Построим ход луча, распо-
ложенноо выше оси пуча (рис. 14.9.5).
На основании заона преломления
n sin α
1
= sin γ
1
.
Уол падения на вторую раницу
α
2
= γ
1
, та а ∆ AOB — равнобедрен-
ный. По условию задачи = 4, сле-
3
2R
3
--------
3
⎝
⎛
r
2
2
r
1
2
⎠
⎞
3
4
---
⎝
⎛
3
-
⎠
⎞
R
r
B
S
O
Рис. 14.8.11
1
1
1
2
2
O
D
A
B
C
r
1
r
2
Рис. 14.9.5
S
2
S
1
------
1
sin
2
α
-------------- -
S
2
S
1
------

634
довательно, = 4, де r
2
и r
1
— радиусы сечений на выходе и вхо-
де света, отуда = 2.
С друой стороны, из ∆AOC и ∆BOD находим
r
1
= R sin α = R sin α
1
, r
2
= R sin β,
де R — радиус пузырьа воздуха. Поэтому
= = 2.
Найдем уол β. Из рисуна видно, что
∠COA + ∠AOB + ∠BOD = 180°,
тода запишем
α
1
+(180° –(γ
1
+ α
2
)) + β = 180°,
та а α
2
= γ
1
, β =2γ
1
– α
1
;
По условию задачи пучо света узий. Из этоо следует, что все
улы малы, поэтому отношение синусов можно заменить отноше-
нием улов:
Решив данную систему уравнений, получим о т в е т:
n =1,5.
πr
2
2
πr
1
2
-------- -
r
2
r
1
-----
R βsin
R α
1
sin
--------------------
βsin
α
1
sin
----------------
=2,
n sin α
1
= sin γ.
2γ
1
α
1
−()sin
α
1
sin
------------------------------------
=2,
nα
1
= γ
1
.
2γ
1
α
1
−
α
1
----------------------
635
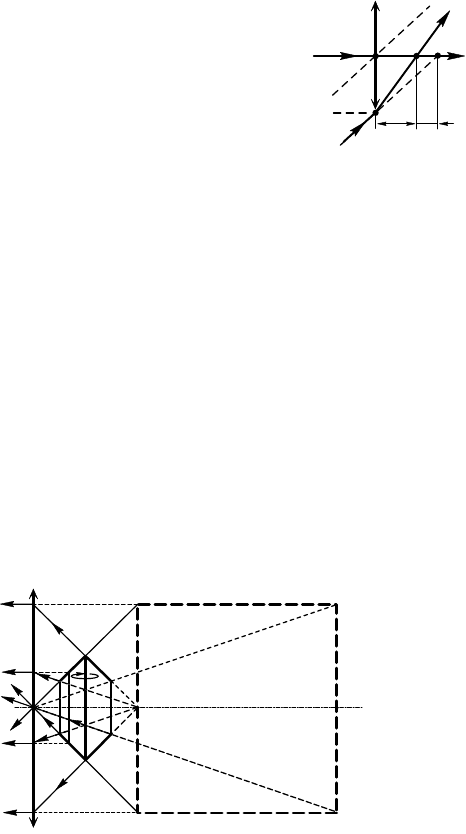
14.11.7. Без линзы пучо световых лучей
сходится в точе A, с линзой — в точе A′
(рис. 14.11.2); A — «мнимый» предмет, A′ —
действительное изображение. Из формулы линзы
=– +
найдем F = = 60 см.
О т в е т: F = 60 см.
14.12.7. Запишем формулу линзы и увеличение для трех поло-
жений предмета:
=–, Г
1
=; = +,
Г
2
=; = –, Г
3
=,
де CO =.
Решив данную систему уравнений, получим о т в е т:
Г
3
==12.
14.12.11. Из симметрии (рис. 14.12.6) видно, что основание AB
трапеции находится от линзы на расстоянии d
AB
= F/2. Из форму-
Рис. 14.11.2
C
D
x
h
b
O
A
A
′
1
F
--- -
1
bx+
------------
1
b
---
bb x+()
x
-------------------- -
F
O
D
A
B
C
D
2
C
2
O′
B
′
A
′
D
′
C
′
C′′
D
′′
Рис. 14.12.6
1
F
--- -
1
AO
---------
1
f
1
---- -
f
1
AO
---------
1
F
--- -
1
BO
-------- -
1
f
2
---- -
f
2
BO
-------- -
1
F
--- -
1
CO
--------
1
f
3
---- -
f
3
CO
--------
AO BO+
2
------------------------
2Г
1
Г
2
Г
2
Г
1
−
------------------ -
636
лы линзы = – найдем расстояние от линзы до изобра-
жения основания C′D′ трапеции:
f
A′B′
= F.
Из соотношения = определим высоту изображения:
A′B′ =2AB.
Основание CD трапеции расположено от линзы на расстоянии
d
CD
= d
AB
+ h = F. Из формулы линзы = – найдем рас-
стояние от линзы до C′D′:
f
C′D′
=3F.
Сторона B′C′ = f
C′D′
– f
A′B′
= 2F. Следовательно, площадь изобра-
жения, имеющео вид прямоуольниа,
S
1
= A′B′ · B′C′ = 2 AB ·2F =4 AB · F.
Если трапецию повернуть на 180°, то сторона CD будет находиться
от линзы на расстоянии d
C′′D′′
= f
AB
– h = F/4. Из формулы линзы
= – определим расстояние от линзы до изображения
стороны C′′D′′:
f
C′′D′′
= F/3.
Высота изображения, имеющео вид трапеции,
H = f
A′B′
– f
C′′D′′
= F – = F.
Из соотношения = = следует, что CD =. Из от-
ношения сторон = = = найдем основание C′′D′′
трапеции:
C′′D′′ = CD = AB.
Площадь изображения, имеющео вид трапеции:
S
2
= H
= = AB · F.
1
F
--- -
1
d
AB
----------
1
f
A′ B′
----------- -
A′B′
AB
------------
f
A′B ′
d
AB
----------- -
3
4
---
1
F
--- -
1
d
AB
----------
1
f
C′ D′
------------
1
F
--- -
1
d
C′′D′′
--------------- -
1
f
C′′D′′
-------------- -
F
3
--- -
2
3
---
CD
AB
---------
F/4
F/2
---------- -
1
2
---
AB 2⁄
CD
C′′D′′
----------------
f
C′′ D′′
d
C′′D′′
--------------- -
F/3
F/4
---------- -
4
3
---
4
3
---
2
3
---
A′B′ C″D″+
2
--------------------------------- -
2AB 2AB/3+
2
---------------------------------------
2F
3
-------
8
9
---
637
Вычислим отношение площадей:
= = 4,5.
О т в е т: = 4,5; рис. 14.12.6.
14.13.3. Один из лучей 1 на-
правим по лавной оптичесой оси
O
1
O
2
друой 2 под произвольным
улом ней. Строим побочную оп-
тичесую ось O
3
O
4
, параллельную
падающему лучу, и фоальную
плосость. Преломленный луч
а будто бы вышел из точи F
1
.
Мнимое изображение находится в
точе S
1
(рис. 14.13.9).
О т в е т: рис. 14.13.9.
14.13.8. На рис. 14.13.10
изображены: O
1
O
2
—
лавная оп-
тичесая ось, 1 — луч, падающий
на линзу, 2 — луч, преломленный
линзой. Для определения положе-
ния линзы продолжим лучи 1 и 2
до их пересечения (точа C). Лин-
за расположена перпендиулярно
лавной оптичесой оси и прохо-
дит через точу C.
Таой ход лучей возможен, если линза рассеивающая. Для тоо
чтобы определить положение ее фоуса, проводим побочную опти-
чесую ось O
3
O
4
и фоальную плосость A. Продолжение прелом-
ленноо луча дает положение фоуса. Для нахождения второо фо-
уса поступим аналоично.
О т в е т: рис. 14.13.10.
14.14.4. Формула линзы:
D = + ⇒ = D –= .
Расстояние до изображения:
f = = –5,6 см;
f < 0, изображение предмета мнимое.
Увеличение линзы равно
Г= = , Г= =0,44.
О т в е т: f = –5,6 см; Г = 0,44.
S
1
S
2
------
4 AB F⋅
8 AB F/9⋅
------------------------------
S
1
S
2
------
Рис. 14.13.9
Рис. 14.13.10
F
S
F
1
O
4
O
2
1
O
3
O
1
2
S
1
A
O
1
O
2
O
3
O
4
F
C
1
2
1
d
---
1
f
---
1
f
---
1
d
---
Dd 1−
d
------------------
d
Dd 1−
------------------
H
h
---- -
f
d
----- -
1
Dd 1−
-------------------- -
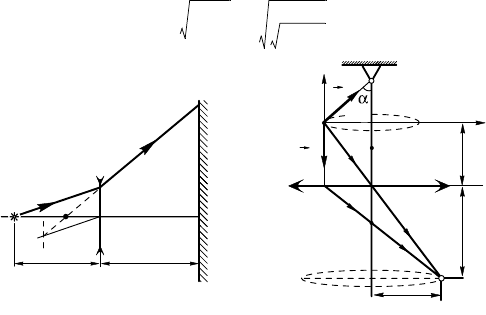
638
14.14.9. Для рассеивающей линзы точа пересечения лучей
сходящеося пуча — это мнимый источни, поэтому
–=–+ (f=Fпо условию).
Для собирающей линзы
=+.
Решив данную систему уравнений, получим f ==3см.
О т в е т: f = 3 см.
14.14.12. Построим изображение источниа света S′ и светлое
пятно на эране (рис. 14.14.1). Та а ∆ S′AO f ∆ S′A′O′, то
=. (1)
Из формулы линзы = – и уравнения (1) получим о т в е т:
D
2
= D
1
1 + + = 7 см.
14.15.2. На шари при движении по оружности радиусом R
0
действуют сила тяжести mg и сила натяжения нити T. Уравнения дви-
жения шариа (рис. 14.15.2) в проециях на OX и OY соответственно:
mω
2
R
0
= T sin α,
0=T cos α – mg,
де ω — уловая сорость шариа. Решив эту систему уравнений,
получим
ω == .
1
F
--- -
1
d
---
1
F
--- -
1
F
--- -
1
d
---
1
f
---
F
3
--- -
D
2
D
1
------ -
lf+
f
----------
1
F
--- -
1
d
---
1
f
---
⎝
⎛
l
d
---
l
d
---
⎠
⎞
g tg α
R
0
---------------
g
l
2
R
0
2
−
--------------------- -
d
l
S
A
O
F
S’
A’
O
’
Рис. 14.14.1
T
Y
R
0
mg
X
F
O
F
d
R
f
Рис. 14.15.1
639
Формула линзы
+=,
де f — расстояние от линзы до плосости вращения изображения.
Следовательно, f =.
С друой стороны, увеличение линзы
Г= , илиГ= ,
отуда находим о т в е т:
ω = l
2
–
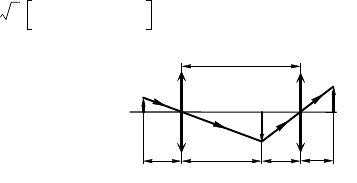
14.17.2. Расположим линзы
на расстоянии l дру от друа
(рис. 14.17.1). Предмет AB нахо-
дится на расстоянии d
1
от первой
линзы. Формула линзы для этоо
случая:
=+.
Изображение A
1
B
1
является предметом для второй линзы, для
нее формула линзы имеет вид:
=+= +.
Сложим полученные равенства:
+=++ +.
По условию задачи линзы сложены вместе, т. е. l=0, а = D.
Оптичесая сила системы
D
0
= D
1
+ D
2
=+,
де d
1
— расстояние от предмета до системы, f
2
— расстояние от
системы до изображения, или
D
0
=+=.
Отсюда находим фоусное расстояние системы:
F =.
1
d
---
1
f
---
1
F
--- -
dF
dF−
-------------
f
d
---
R
R
0
-------
g
R
2
df−()
2
F
2
---------------------------
14/−
d
1
B
B
1
l
A
A
1
d
2
f
1
f
2
B
2
A
2
Рис. 14.17.1
1
F
1
------
1
d
1
----- -
1
f
1
---- -
1
F
2
------
1
d
2
----- -
1
f
2
---- -
1
lf
1
−
-------------
1
f
2
---- -
1
F
1
------
1
F
2
------
1
d
1
----- -
1
f
1
---- -
1
lf
1
−
-------------
1
f
2
---- -
1
F
--- -
1
d
1
----- -
1
f
2
---- -
1
F
1
------
1
F
2
------
1
F
--- -
F
1
F
2
F
1
F
2
+
-------------------
