Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.


620
де U
1
, U
2
, U
3
— амплитуды напряжений на обладах аждоо из
онденсаторов. Отсюда
U
1
= C .(4)
К моменту времени t
1
энерия онденсатора C
1
стала
W
1
=cos
2
ωt =cos
2
ωt. (5)
Эта энерия при пробое переходит в теплоту. Следовательно, энерия
олебательноо онтура уменьшается на величину W
1
: W = W
0
– W
1
.
С учетом выражений (2) и (5) имеем
W =1– cos
2
ωt . (6)
Амплитуда q
0
олебаний заряда после пробоя онденсатора мо-
жет быть определена из соотношения
W =, (7)
де C′ — емость батареи из соединенных последовательно онден-
саторов C
2
и C
3
:
C′ =. (8)
Подставляя (1), (3) и (8) в выражение (7), получаем q
0
. Учиты-
вая ромоздость выражений, предварительно вычислим С, C′ и ω:
C =200мФ, C′ = 400 мФ, ω = 10
4
рад/с.
Теперь находим о т в е т:
q
0
=2·10
–3
Кл = 2 мКл.
13.2.16. Напряжение в сети переменноо тоа
u = U
m
sin ωt,
де U
m
= U
д
— масимальное значение напряжения в сети, ω =
=2πν, U
д
— действующее значение напряжения. За время одноо
полупериода лампоча будет ореть в течение
∆t = t
2
– t
1
,
U
C
1
------
C
1
U
1
2
2
--------------
C
2
U
2
2C
1
--------------
CU
2
2
------------
⎝
⎛
C
C
1
------
-
⎠
⎞
q
0
2
2C′
---------
C
2
C
3
C
2
C
3
+
-------------------
2
621
де t
1
, t
2
— моменты времени зажиания и ашения лампочи соот-
ветственно, оторые найдем из условий
U
0
= U
д
sin (2πνt
1
), t
2
=–t
1
,
де T = — период олебаний тоа. Отсюда получаем
t
1
= arcsin d 1,67 · 10
–3
с,
t
2
=–t
1
d 8,33 · 10
–3
с,
∆t d 6,66 · 10
–3
с.
Следовательно, за время ∆τ = 1 мин лампоча будет ореть в
течение времени
τ =2 ∆t =2ν∆τ∆t d 40 с.
13.2.34. Полное сопротивление цепи
Z =.
Из заона Ома для участа цепи
I
0
=,
де I
0
, U
0
— амплитудные значения силы тоа и напряжения. Связь
между действующим и амплитудным значениями напряжения выра-
жается формулой
U
0
= U
д
.
Находим амплитудное значение силы тоа
I
0
= d 17,2 А
и действующее значение силы тоа
I
д
== d 12,3 А.
Средняя мощность переменноо тоа
N = U
д
I
д
cos ϕ.
2
T
2
----
1
ν
---
1
2πν
----------
U
0
2U
д
---------------
1
2ν
-------
∆τ
T
------
R
2
2πνL 1/ 2πνC()−()
2
+
U
0
Z
------ -
2
2U
д
R
2
2πνL 1/ 2πνC()−()
2
+
------------------------------------------------------------------------- -
I
0
2
-------
U
д
R
2
2πνL 1/ 2πνC()−()
2
+
------------------------------------------------------------------------- -
622
Коэффициент мощности cos ϕ можно найти, воспользовавшись
выражением для сдвиа фаз между тоом и напряжением:
tg ϕ == = .
Отсюда получим
cos ϕ =
и
N = d 2250 Вт.
О т в е т: I
0
d 17,2 A; I
д
d 12,3 A; N d 2250 Вт.
13.2.39. Полное сопротивление цепи
Z =,
де X
L
= ωL, X
C
=1/(ωC) — реативные сопротивления атуши и
онденсатора соответственно, ω =2πν. Поэтому
Z = d 111,6 Ом.
Сдви фаз между тоом и напряжением
ϕ = arctg = arctg d 89°.
Минимальное сопротивление цепи
Z
min
= R =2Ом
при частоте ν
0
, для оторой реативное сопротивление равно нулю:
2πν
0
L– πν
0
C =0,
отуда
ν
0
= d 142,4 Гц.
О т в е т: Z d 111,6 Ом; ϕ d 89°; Z
min
= 2 Ом; ν
0
d 142,4 Гц.
ϕsin
ϕcos
------------ -
1cos
2
ϕ−
ϕcos
-----------------------------
2πνL 1/ 2πνC()−
R
-------------------------------------------------
R
R
2
2πνL 1/ 2πνC()−()
2
+
------------------------------------------------------------------------- -
U
д
2
R
R
2
2πνL 1/ 2πνC()−()
2
+
------------------------------------------------------------------------- -
R
2
X
L
X
C
−()
2
+
R
2
2πνL 12πνC()⁄−()
2
+
ωL 1/ ωC()−
R
-----------------------------------
2πνL 1/ 2πνC()−
R
-------------------------------------------------
1
2
---
1
2π LC
------------------- -
623
13.4.13. Частота олебаний онтура ν = . Находим диа-
пазон частот онтура: от ν
1
= = 22,2МГц до ν
2
= =
=16МГц.
13.4.19. Частота собственных олебаний в онтуре
ω
0
=. (1)
По заону сохранения энерии
=. (2)
Решая (1) и (2), находим
I
m
=, или ω
0
=.
Следовательно, длина волны, на оторую настроен олебатель-
ный онтур, и емость онденсатора соответственно равны:
λ == d 37,7 м,
C ===2·10
–9
Ф,
де c =3·10
8
м/с — сорость света.
О т в е т: λ d 37,7 м; С = 2
.
10
–9
Ф.
1
2π LC
------------------- -
1
2π LC
1
-----------------------
1
2π LC
2
-----------------------
1
LC
------------
LI
m
2
2
---------- -
q
m
2
2C
-------
q
m
LC
------------
I
m
q
m
------ -
2πc
ω
0
----------
2πcq
m
I
m
----------------- -
1
ω
0
2
L
---------- -
q
m
2
I
m
2
L
---------- -

624
Ч АСТЬ 4
ОПТИКА
Г л а в а 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
14.2.2. Выберем два произвольных
луча SA и SB, падающих на зерало
(рис. 14.2.8). Отраженные лучи построим,
используя заон отражения. Заметим, что
они расходятся и пересеутся тольо их
продолжения в точе S
1
, оторая является
мнимым изображением точи S, та а в
ней пересеутся продолжения любых дру-
их отраженных от зерала лучей. Поа-
жем это. Треуольнии SAB и S
1
AB имеют
общую сторону AB и пары равных улов ∠ SAC = ∠ S
1
AC, ∠ SBC =
= ∠ S
1
BC ∠SAC =–α
1
, ∠S
1
AC = – δ
1
, но δ
1
= β
1
а улы верти-
альные, а β
1
= α
1
по заону отражения . Следовательно,
∆ SAB = ∆ S
1
AB.
Из равенства треуольниов следует равенство высот, опущенных
на сторону AB. Для любых ∆SAB высотой является перпендиуляр
зералу (или ео продолжению), равный расстоянию SC, и любые лучи
отразятся от зерала та, что их продолжения пройдут через точу S
1
,
оторая и будет изображением точи S. Это изображение мнимое —
ео можно видеть, фоторафировать, но получить на эране нельзя.
О т в е т: изображение мнимое; рис. 14.2.8.
14.2.3. Построим симметричный
отрезо A
1
B
1
(опустим перпендиуляры
AA
2
и BB
2
на плосость зерала и отло-
жим на них равные отрези AA
2
=
= A
2
A
1
и BB
2
= B
2
B
1
). Соединим точи
A
1
и B
1
, A
1
B
1
—
мнимое изображение
отреза AB (рис. 14.2.9).
Для тоо чтобы видеть изображе-
ние аой-либо точи предмета в зер-
але, необходимо, чтобы в отраженном
потое лучей, идущих из этой точи на
зерало, нашлись бы лучи, попадаю-
Рис. 14.2.8
⎝
⎛
π
2
---
π
2
---
⎠
⎞
Рис. 14.2.9
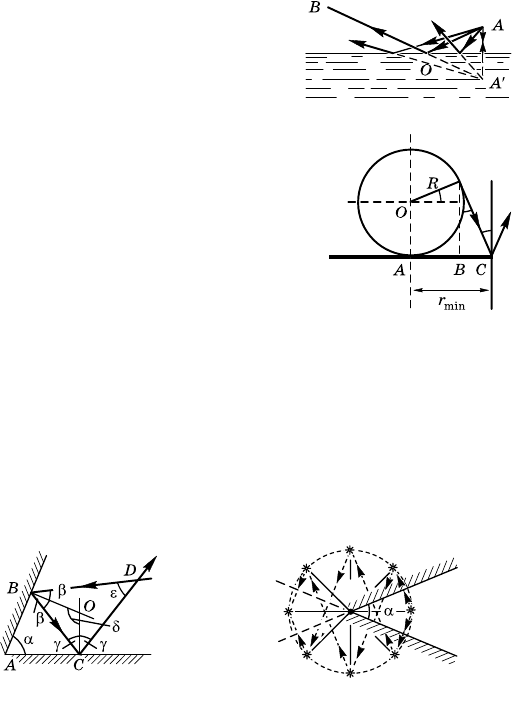
625
щие в лаз наблюдателя. В данном примере в лаз должны попасть
отраженные лучи, идущие из точе A и B.
Чтобы видеть весь предмет, лаз наблюдателя следует располо-
жить та, чтобы в нео моли попасть лучи, дающие изображения
точе A и B. Ка видно из чертежа, пространство, в аждой точе
отороо встречаются эти лучи, удовлетворяющие таому условию,
залючено внутри затемненноо треуольниа (см. рис. 14.2.9).
Ответ: рис.14.2.9.
14.2.5. Построим изображение ис-
точниа света (лампы) — точу A′, за-
тем построим прямую, соединяющую
точи A′ и B: точа O пересечения этой
прямой с поверхностью воды будет ис-
омой точой (рис. 14.2.10).
О т в е т: точа О.
14.2.14. Из рисуна 14.2.11 видно, что
r
min
= AB + BC,
де AB = R cos ϕ и BC =(R + R sin ϕ)tg ϕ.
Следовательно,
r
min
= R [cos ϕ +(1+sinα)tg α]=26см.
О т в е т: r
min
= 26 см.
14.3.1. На рисуне 14.3.5 β — уол па-
дения луча на плосость AB, а γ — уол па-
дения луча на плосость AC. В треуольни-
е BCO β + γ = π – δ. Та а OB ⊥ AB, а
OC ⊥ AC, то в четырехуольние ABOC уол δ = π – α. Таим образом,
β + γ = π – δ = α.
Из треуольниа BCD получаем, что исомый уол
ε = π – 2(β + γ)=π –2α.
О т в е т: ε = π – 2α.
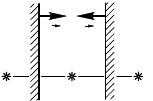
14.3.4. Светящаяся точа даст два мнимых изображения S
1
и S
2
,
расположенных относительно зерал OA и OB симметрично точе S
(рис. 14.3.6).
Рис. 14.2.10
Рис. 14.2.11
Рис. 14.3.5
S
A
B
S
1
S
4
S
5
S
7
S
6
S
3
S
2
O
Рис. 14.3.6
626
Из равенства треуольниовAOS, BOS, AOS
1
, BOS
2
следует, что
изображения S
1
и S
2
лежат на дуе оружности с центром в точе O и
радиусом R = OS. При этом ∠ SOS
1
= α. Мнимый источни света S
1
отражается в зерале OB, давая изображение S
3
, лежащее на той же
оружности, причем ∠ SOS
3
=2α =90°. Аналоично образуется
изображение S
4
источниа S
2
в зерале OA. Следующие изображе-
ния S
5
и S
6
образуются та же, а ∠ SOS
5
= ∠SOS
6
= 3α =135°.
Изображения S
5
и S
6
, отражаясь в зералах OB и OA соответствен-
но, дадут изображения, оторые наложатся дру на друа в точе S
7
.
Следовательно, будет семь изображений точи S, т. е. N = 7.
О т в е т: N = 7.
14.3.5. Расстояние |AO| (рис.14.3.7) между
неподвижным источниом света O и движу-
щимся равномерно со соростью v
1
зералом из-
меняется со временем по заону |AO| = x
0
– v
1
t.
Расстояние |OO′| между источниом O и ео
изображением |O′| равно удвоенному расстоя-
нию AO|:
|OO′|=2|AO|=2x
0
–2v
1
t,
а расстояние между изображениями O′ и O″ равно учетверенному
расстоянию |AO|:
|O′O′′|=4|AO|=4x
0
–4v
1
t.
Таим образом, изображения O′ и O′′ сближаются со соростью
v =4v
1
. Следовательно,
v
1
= = 1,25 м/с.
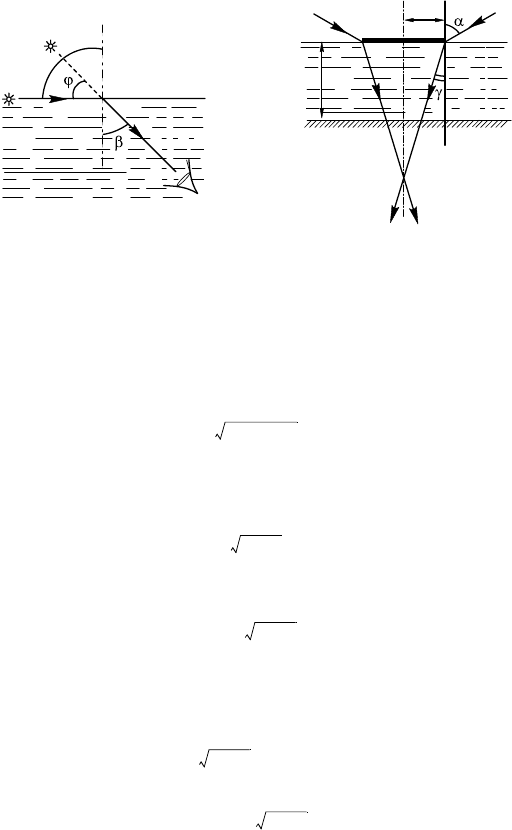
14.5.1. Из рисуна 14.5.3 видно, что уол падения солнечных
лучей α =90°. Из заона преломления = n, или = n, оту-
да sin β = = 0,75; β d 49°. Следовательно, пловец видит солнце
под улом
ϕ = α – β =41°
поверхности воды.
14.5.11. Если направить на рай плота в т. A луч света под
улом α, то раница тени будет проходить через т. B (рис. 14.5.4).
Отрезо OB = OC – CB. Далее находим (см. ∆ ABC):
OB = R – AC tg γ = R – h tg γ.
O
O′′
O′
A
B
v
1
v
1
Рис. 14.3.7
v
4
---
αsin
βsin
------------ -
1
βsin
------------
1
n
---
627
Из заона преломления запишем
sin γ =,
де n — поазатель преломления воды. Тода
tg γ = .
В точу A свет попадает под разными улами, но самое большое
значение ула преломления γ будет при α → 90°, тода sin α → 1 и
tg γ =.
Поэтому
OB = R –.
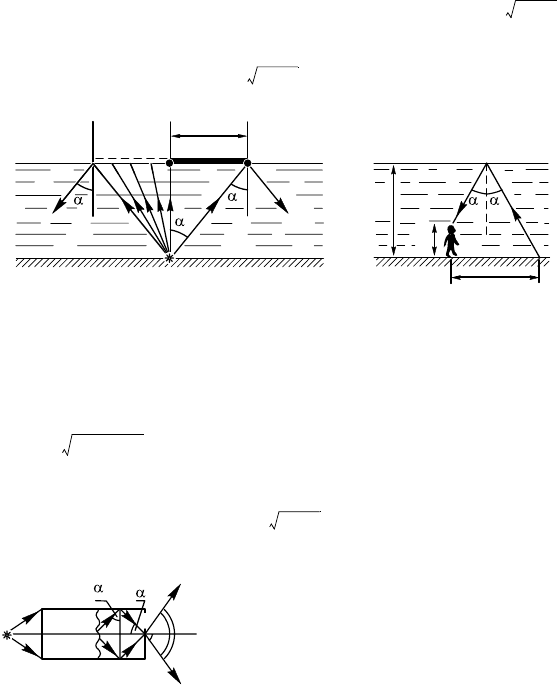
При освещении плота рассеянным светом в воде образуется о-
нус с вершиной D, внутрь нео свет попасть не может — там тень.
На дне образуется темный ру, радиус отороо
r = R – d 0,72 м.
Задача имеет решение, если R l , в противном случае дно
будет равномерно освещено.
О т в е т: r d 0,72 м.
αsin
n
------------ -
αsin
n
2
sin
2
α−
--------------------------------
1
n
2
1−
--------------------
h
n
2
1−
--------------------
Рис. 14.5.4
D
R
A
B
C
h
O
α
Рис. 14.5.3
h
n
2
1−
--------------------
h
n
2
1−
--------------------
628
14.6.1. Та а sin α =, то sinα
р
==0,66; α
р
=41,5°;
sin α
ф
= = 0,65; α
ф
=40,8°.
О т в е т: α
р
= 41,5°; α
ф
= 40,8°.
14.6.4. Из ∆SOA находим радиус, удовлетворяющий условию
(рис. 14.6.1) R = Htg α
0
. Та а sin α
0
= , то tg α
0
= .
Поэтому
R = = 3 м.
Ответ: R = 3 м.
14.6.8. Из еометрии рисуна 14.6.2
s = (H – h)tg α
0
+ Htg α
0
,
де α
0
— предельный уол полноо внутреннео отражения; sin α
0
= ,
tg α
0
= .
Решив данную систему уравнений, получим о т в е т:
s = .
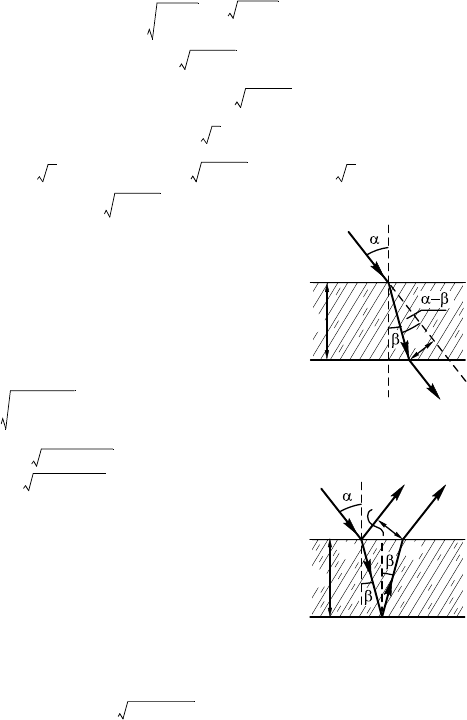
14.6.12. Внутри световода распрост-
раняются тольо лучи, падающие на ео
боовую поверхность под улом α l α
0
(рис. 14.6.3).
Луч, вышедший через центр торца све-
товода, в точе A претерпел полное внут-
реннее отражение, поэтому уол падения
α =90° – α
0
.
1
n
---
1
n
р
-------- -
1
n
ф
------ -
1
n
---
1
n
2
1−
--------------------
H
n
2
1−
--------------------
R
A
O
H
0
0
0
Рис. 14.6.1
H
00
h
s
Рис. 14.6.2
1
n
---
α
0
sin
1sin
2
α
0
−
------------------------------- -
2Hh−
n
2
1−
--------------------
S
A
O
0
δ
Рис. 14.6.3
629
Уол преломления γ найдем из заона преломления:
sin γ = n sin α = n sin(90° – α
0
)=n cos α
0
.
Уловая апертура выходящео пуча β =2γ. Известно, что
sin α
0
=.
Тода
cos α
0
== ,
sin γ =.
Это уравнение имеет решение, если 0 mm1. Следовательно,
1<n m .
Если 1 < n <, то β = 2 arcsin ; если n =, то β = 180°.
О т в е т: β = 2 arcsin .
14.7.2. Смещение луча l = AB sin (α – β),
де β — уол преломления луча в стеле
(рис. 14.7.3). Находим толщину пластини:
d = AB cos β =.
Соласно заону преломления sin β = ,
т. е. cos β = , поэтому
d = d 39 мм.
О т в е т: d d 39 мм.
14.7.3. Соласно заону преломления
= n. Из ∆ DAC (рис. 14.7.4) сторона DA =
= d tg β, а BA =2DA = 2α tg β, тода
l=BA sin(90° – α).
Из приведенных уравнений получим о т в е т:
l = = 1,5 см.
1
n
---
1
1
n
2
------
−
n
2
1−
n
--------------------
n
2
1−
n
2
1−
2
2 n
2
1− 2
n
2
1−
l
d
A
B
Рис. 14.7.3
l
d
A
B
C
D
Рис. 14.7.4
l βcos
αβcossin αβsincos−
-----------------------------------------------------------
αsin
n
------------ -
1
sin
2
α
n
2
-------------- -
−
ln
2
sin
2
α−
α n
2
sin
2
α−αcos−()sin
--------------------------------------------------------------------
αsin
βsin
------------ -
d 2αsin
n
2
αsin
2
−
------------------------------
