Турчина Н.В. Физика в задачах для поступающих в вузы

Подождите немного. Документ загружается.

610

Запишем уравнения движения протона вдоль нормали n  трае-

тории и оси Z, параллельной веторам E и B (рис. 12.2.14):

= F

, ma

= F

эл

или

= qv

B, ma

= qE.

Составляющая сорости, перпендиулярная направлению по-

лей, при движении частицы не изменяется.

Вдоль оси Z протон будет двиаться с постоянным усорением

и расстояние, пройденное им вдоль оси Z,

s =.

Радиус R спирали и период T обращения соответственно равны:

R = , T ==.

Расстояния, пройденные протоном вдоль силовых линий за вре-

мя первоо и второо оборотов:

== , s

=–= .

-----------

Рис. 12.2.14

--------

-----------

2πR

-----------

2πm

------------

------------ -

2π

--------------------

2T()

--------------------- -

------------ -

32π

mE⋅

2qB

----------------------------

611

Эти расстояния равны соответствующим шаам витов. Поэтому

==3.

Ответ: = 3.

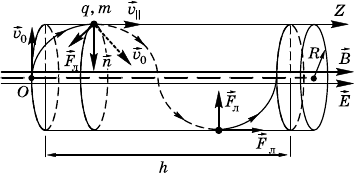
12.2.33. На α-частицу при движении будут действовать сила

Лоренца

= q

⊥

B = q

sin β) B

и сила элетричесоо поля

эл

= q

Запишем уравнения движения α-частицы вдоль нормали n 

траетории и оси Z, параллельной веторам E и B:

= F

, m

= F

эл

или

= q

⊥

B, m

= q

де составляющая сорости, перпендиулярная направлению по-

лей, v

⊥

= v

sin α.

Вдоль оси Z α-частица будет двиаться с усорением

и расстояние, пройденное частицей вдоль оси Z,

s = v

t + = v

cos βt +.

Радиус R спирали и период T обращения соответственно

равны:

R == , T == .

----- -

-----

----- -

⊥

-------------- -

⊥

-------------- -

---------- -

-----------

⊥

-------------- -

βsin

----------------------------

2πR

⊥

-----------

2πm

----------------

612

Расстояния, пройденные α-частицей вдоль силовых линий за

время первых четырех и пяти оборотов:

=(v

cos β) · 4T += + ,

=(v

cos β) · 5T += + .

Следовательно, ша пятоо вита спирали

h = s

– s

= v

cos β + = v

cos β + d 53 мм.

О т в е т: h d 53 мм.

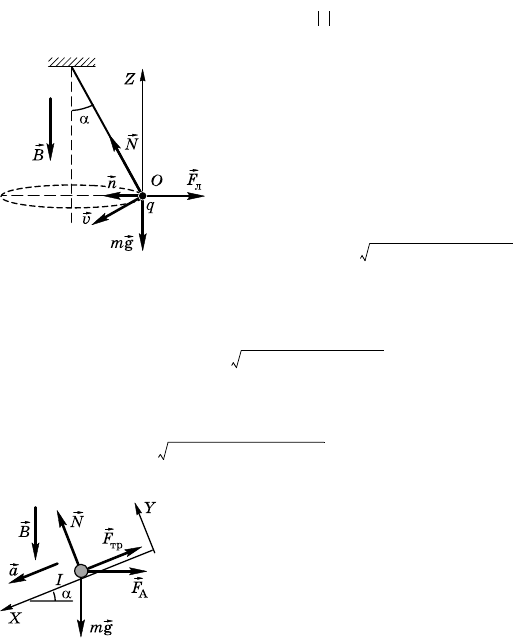
12.2.35. Уравнения движения ша-

риа в проеции на нормаль n  траето-

рии и ось OZ (рис. 12.2.15):

= Nsin α – qvB, 0 = Ncos α – mg,

де F

= qvB.

Решив данную систему уравнений,

получим

v =.

Тода период обращения шариа

T == .

Та а R = lsin α, то

T = d 1,31 с.

О т в е т: T d 1,31 c.

12.3.12. На стержень действуют следую-

щие силы: тяжести mg, реации опоры N, тре-

ния F

тр

между стержнем и поверхностью на-

лонной плосости и Ампера F

(рис. 12.3.7).

Запишем второй заон Ньютона в прое-

циях соответсвенно на оси OX и OY:

ma = mg sin α – F

тр

– F

cos α,

0 = N – mg cos α – F

sin α.

4T()

--------------------- -

βcos πm

------------------------------------

32π

-------------------------- -

5T()

--------------------- -

10v

βcos πm

---------------------------------------

50π

-------------------------- -

2πm

----------------

⎝

⎛

9πE

----------- -

⎠

⎞

4πm

---------------

⎝

⎛

9πE

----------- -

⎠

⎞

Рис. 12.2.15

-----------

qB− q

g tg α/R++

2m/R

-------------------------------------------------------------------------------

2πR

-----------

4πm

g tg α/R+ qB−

------------------------------------------------------------------------- -

4πm

g/ l cos α()+ qB−

-------------------------------------------------------------------------------

Рис. 12.3.7

613

Та а F

тр

= μN, а сила Ампера F

= IBl, то, решив систему

приведенных уравнений, получим

a = g(sin α – μ cos α)– (μ sin α +cosα) d 2,2 м/с

О т в е т: a d 2,2 м/с

12.3.23. На проводни действует сила Ампера. Направление

этой силы совпадает с направлением перемещения проводниа.

Следовательно, работа силы Ампера:

A = F

l = IBLl =8мДж.

При движении проводниа в манитном поле сила тоа не оста-

ется постоянной. Для ее поддержания необходим источни тоа.

Работа источниа по поддержанию постоянноо тоа и будет равна

найденной работе A.

О т в е т: A = 8 мДж.

12.4.6 .

Манитный момент вита:

= IS = IπR

d 0,04 А · м

Механичесий момент силы:

= p

B sin α,

де α — уол, оторый составляет нормаль  плосости онтура с

направлением поля. В нашем случае α = π/2 – β. Поэтому

= IπR

B sin (π/2 – β)=IπR

B cos β d 2 · 10

–3

Н · м.

О т в е т: p

d 0,04 А

; M

d 2

–3

м.

12.4.7. Сила F

, действующая на сторону DC, равна нулю. Си-

ла, действующая на сторону AD, равна F

= BI · AD sin α = BIh, де

h = AD sin α — высота треуольниа, опущенная на сторону DC (см. в

условии рис. 12.4.1). Аналоично сила, действующая на сторону AC,

равна F

= BI · AC sin β = BIh = F

. Силы F

и F

перпендиулярны

плосости треуольниа, направлены в противоположные стороны

и приложены  серединам сторон AD и AC. Следовательно, вращаю-

щий момент образуемой ими пары сил

M = BIh ·.

IBl

--------- -

---------

614

Учитывая, что h ·=S, получаем

M = BIS.

О т в е т: F

= F

= BIh; M = BIS.

12.4.8. Контур состоит из пяти прямолинейных проводниов,

по оторым теут тои. Обозначим длину стороны вадрата через l.

По заону Ома силы тоов в проводниах:

==; I

== .

Проводнии ab и cd расположены параллельно полю, поэтому

=0 и F

= 0, та а sin α =0. Проводнии bc и ad перпендиу-

лярны полю, и на них действуют силы Ампера:

= F

= BI

та а в этом случае уол α =90° и sin α = 1. Проводни ac состав-

ляет с ветором индуции уол α =45°, ео длина l , следователь-

но, со стороны поля на нео действует сила

= BI

l sin 45°,

направленная в ту же сторону, что и силы F

и F

. Равнодействую-

щая этих трех параллельных сил

F =2F

+ F

= Bl(2I

+ I

точа ее приложения совпадает с центром онтура. Подставив вы-

ражения для сил тоов I

и I

, получаем: F = =

=15,5Н.

О т в е т: F = 15,5 H; cила направлена перпендиулярно плос-

ости рисуна.

12.4.12. Выделим малый элемент ольца протяженностью ∆l. На

этот элемент действуют сила Ампера и упруие силы (рис. 12.4.4). Рас-

сматриваемый элемент достаточно мал, и можно приближенно счи-

тать, что сила Ампера ∆F

= IB∆l. Та а элемент ольца находится в

равновесии, то ∆F

=2T sin α. Длина элемента

ольца через центральный уол равна ∆l = R ·2α,

а сила T = σS. Та а уол α мал, то sinα d α.

Поэтому IBR · 2α = 2σS · α, отуда находим

ответ:

B ==2,3Тл.

---------

abc

----------- -

2ρl

---------

-------- -

2ρl

-------------

BUS 12+()

2ρ

------------------------------------

Рис. 12.4.4

σS

--------

615

12.9.11. Манитный пото Ф, пронизывающий поверхность

площадью S = πr

(l =2πr), равный Ф = BS, изменяется со временем

по заону

Ф=αt .

ЭДС элетроманитной индуции и сила тоа соответственно

равны:

|= = ,

I == .

При этом в ольце из проволои выделится мощность

P = I

R = d 2·10

–13

Вт.

О т в е т: P = 2 · 10

–13

Вт.

12.9.14. При введении онтура в манитное поле площадь,

пронизываемая силовыми линиями поля, будет увеличиваться по

заону S = ax, де x — длина части онтура, находящейся в зазо-

ре: x = vt.

Манитный пото, пронизывающий поверхность S,

Ф=BS = Bavt

будет изменяться, что приведет  появлению в онтуре ЭДС |1

| и

силы тоа I:

| = = Bav, I == .

Количество теплоты, выделившейся в онтуре сопротивле-

нием R,

Q = I

= t

де t

= a/v — время введения онтура в зазор. Следовательно,

Q = d 3,5 · 10

–6

Дж.

4π

------ -

dΦ

------- -

αl

4π

---------

------

αl

4πR

-----------

16π

----------------- -

dΦ

------- -

------

Bav

------------

--------------------

-----------------

616

12.9.25. При сольжении перемыч-

и вознинет переменный манитный по-

то Ф = BScos α, та а изменяется пло-

щадь S = lx, де x — оордината пере-

мычи. Это приведет  возниновению в

онтуре ЭДС

|= =BIv cos α

и вызовет появление силы тоа в онтуре и силы Ампера, направ-

ленных та, а поазано на рис. 12.9.20.

По заону Ома сила тоа в онтуре (см. в условии рис. 12.9.13)

равна

I == .

Сила Ампера, действующая на перемычу при ее движении,

= IBl =.

Уравнения движения перемычи в проециях соответственно

на оординатные оси X и Y:

де F

тр

= μN.

Решая систему приведенных уравнений, получаем

a = g(sin α – μ cos α)– (μ sin α +cosα).

Сорость перемычи будет масимальной, ода ее усорение

станет равным нулю:

0=mg(sin α – μ cos α)– (μ sin α +cosα).

Отсюда находим о т в е т:

max

= при μ m tg α.

12.9.26. Если  стержню приложить силу F, то при ео пере-

мещении будет изменяться площадь треуольниа ACD и возни-

Рис. 12.9.20

dΦ

------- -

-------- -

Blv αcos

----------------------- -

v αcos

----------------------------- -

ma = mg sin α – F

cos α – F

тр

0=N – mg cos α – F

sin α,

v αcos

----------------------------- -

max

αcos

--------------------------------------- -

mgR αsin μαcos−()

αμ αsin αcos+()cos

--------------------------------------------------------------------

617

нет изменяющийся со временем пото индуции Ф = BS, де

S = x

sin — площадь онтура. Это приводит  возниновению в

онтуре ЭДС

|= =2Bx sin = 2Bx sin v,

оторая вызовет появление индуционноо тоа I и силы Ампера:

= IB · 2x sin .

По заону Ома сила тоа в стержне

I =,

де R =2ρx sin — сопротивление части стержня между точами

C и D. Следовательно,

I ==. (1)

С учетом выражения (1) запишем соотношение для силы Ампера:

=sin.

Уравнение движения стержня имеет вид

ma = F – F

, или ma = kx – sin .

Сорость стержня будет масимальна, ода ео усорение ста-

нет равным нулю. Следовательно,

0=k – sin .

Отсюда получаем о т в е т:

max

= d 15,45 м/с.

12.10.5. При размыании цепи сила тоа в атуше начнет

уменьшаться, что приведет  изменению манитноо потоа, про-

низывающео вити атуши. При этом в атуше вознинет ЭДС

самоиндуции, среднее значение оторой |1

|=L =18В.

О т в е т: | 1

| = 18 B.

---

dΦ

------- -

---

⎝⎠

⎛⎞

------ -

---

⎝⎠

⎛⎞

---

-------- -

---

2ρx α/2()sin

------------------------------------ -

--------

------------------

---

------------------

---

max

------------------------

---

ρk

α/2()sin

-------------------------------------

∆I

∆t

-------

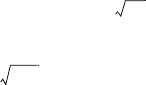
618

12.10.9. Манитный пото, пересеающий все вити атуши,

NФ=LI. Изменение манитноо потоа при неизменной еометрии

атуши обусловлено изменением силы тоа, теущео по атуше.

Поэтому

N∆Ф=L∆I = L(I

– I

отуда

L= = 0,125 Гн.

О т в е т: L = 0,125 Гн.

12.10.10. То в атуше порождает ЭДС индуции , ото-

рой противодействует ЭДС самоиндуции L . Следовательно,

– L = IR,

отуда получаем

∆q = I∆t ==25мКл.

О т в е т: ∆q = 25 мКл.

12.10.19. Энерия манитноо поля внутри соленоида увеличится

от W

= до W

= . По условию задачи

∆W = W

– W

=– .

Отсюда получаем индутивность соленоида:

L = d 1·10

–3

Гн.

О т в е т: L d 1

–3

Гн.

Г л а в а 13. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

И ВОЛНЫ

13.1.7. Частота олебаний в онтуре ν = . Для онденса-

тора 1

= , (1)

N∆Ф

−

-----------------

∆Ф

∆t

-------- -

∆I

∆t

-------

∆Φ

∆t

--------

∆I

∆t

-------

∆Φ ∆I−

∆t

----------------------

--------- -

2∆W

−

-----------------

2π LC

------------------- -

2π LC

-----------------------

619

а для онденсатора 2

=. (2)

Емость последовательно соединенных онденсаторов

C =. (3)

Выражая значения C

и C

из соотношений (1) и (2) и подставляя

в (3), получаем

C =.

Следовательно,

ν == =20Гц.

О т в е т: ν = 20 Гц.

13.1.26. Заон изменения напряжения на онденсаторе:

u = Ucos ωt.

Емость C трех последовательно соединенных онденсаторов

определяем из формулы: = + + , отуда получаем

C =. (1)

Начальная энерия олебательноо онтура

=. (2)

Циличесая частота олебаний в онтуре

ω = . (3)

Та а при последовательном соединении онденсаторов заряд

на аждом из них одинаов и равен заряду батареи, то для началь-

ноо момента времени

q = CU = C

= C

2π LC

-----------------------

-------------------

4π

--------------

----------------- -

2π L

4π

--------------

------------------

--------------------------------------------------

---

------

------------------------------------------------------

------------