Турчина Н.В. Физика в задачах для поступающих в вузы

Подождите немного. Документ загружается.

250

10.15.13. Частица массой m и зарядом q влетает с 8оризонталь-

ной соростью v

в однородное элетричесое поле напряженно-

стью E. Линии напряженности элетричесо8о поля совпадают с

направлением усорения свободно8о падения (рис. 10.15.7). Найди-

те усорение частицы и ее сорость спустя время t. Запишите заон

движения частицы.

 10.15.14. Частица, имеющая заряд q и энер8ию W, влетает в пло-

сий онденсатор параллельно е8о пластинам. Заряд онденсатора Q,

е8о емость C, расстояние между пластинами d. Первоначально

частица находится на одинаовом расстоянии от пластин. Каой

длины должна быть аждая пластина, чтобы частица не упала на ее

поверхность?

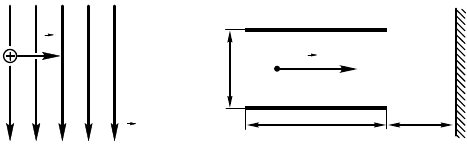
 10.15.15. Элетрон, имеющий инетичесую энер8ию W,

влетает в плосий онденсатор, между пластинами оторо8о под-

держивается разность потенциалов ∆ϕ. Расстояние между пласти-

нами d, их длина l. На расстоянии h от онденсатора находится э-

ран (рис. 10.15.8). Начальная сорость элетрона направлена па-

раллельно пластинам. Найдите смещение элетрона на эране.

10.15.16. Узий пучо элетронов пролетает через плосий

онденсатор параллельно е8о пластинам и вызывает свечение эра-

на, расположенно8о на расстоянии L = 15 см от рая онденсатора.

При подаче на онденсатор напряжения U = 50 В светящееся пятно

на эране смещается на величину H = 21 мм. Расстояние между

пластинами онденсатора d = 18 мм, длина пластин l = 6 см. Опре-

делите сорость элетронов в пуче.

10.15.17. В плосий онденсатор длиной l = 5см влетает

элетрон под у8лом α = 15°  пластинам. Энер8ия элетрона W =

= 1,5 эВ. Расстояние между пластинами d = 1 см. Определите на-

пряжение на онденсаторе, при отором элетрон на выходе будет

дви8аться параллельно пластинам.

Рис. 10.15.8

Рис. 10.15.7

251

10.15.18. Частица массой m = 10

–12

8

и зарядом q = –2 · 10

–11

Кл влетает в верти-

альное однородное элетростатичесое

поле напряженностью E = 40 В/м под у8-

лом ϕ = 120°  силовым линиям со соро-

стью v

= 220 м/с (рис. 10.15.9). Через аой

промежуто времени частица сместится

вдоль силовой линии на расстояние ∆h = 3 м?

Чему равна сорость частицы в этот мо-

мент времени? Силу тяжести не учиты-

вать.

10.15.19. Тело массой m с зарядом q (q > 0) брошено под у8-

лом α  8оризонту с начальной соростью v

. Движение тела про-

исходит одновременно в поле тя8отения и однородном элетро-

статичесом поле напряженностью E, силовые линии оторо8о

направлены вертиально вниз. Определите время полета, даль-

ность полета и масимальную высоту подъема тела над линией

8оризонта.

10.15.20. Частица массой m и за-

рядом q > 0 влетает в плосий онден-

сатор, обладами оторо8о являются

металличесие сети (рис. 10.15.10).

Напряженность поля в онденсаторе

равна E, расстояние между сетами d.

Начальная сорость частицы v

состав-

ляет у8ол α с плосостью первой сети.

С аой соростью и под аим у8лом

 плосости второй сети частица вы-

летит из онденсатора? Силу тяжести

не учитывать.

10.15.21. Заряженная частица с зарядом q влетает в плосий

онденсатор длиной l под у8лом α  плосости пластин, а вылетает

под у8лом β. Определите первоначальную инетичесую энер8ию

частицы, если напряженность поля внутри онденсатора равна E.

Силу тяжести не учитывать.

10.15.22. Элетрон, пройдя усоряющую разность потенциа-

лов ∆ϕ, влетает в плосий воздушный онденсатор параллельно

пластинам длиной l и вылетает из не8о. В тот момент, о8да элет-

рон влетает в онденсатор, в последнем возниает элетричесое

поле, напряженность оторо8о изменяется со временем по заону

E = αt, 8де α — положительная постоянная. Ветор E перпендиу-

лярен пластинам. Определите сорость элетрона, вылетевше8о из

онденсатора. Заряд элетрона |e|, масса элетрона m

. Силой тя-

жести пренебречь.

mq,

Рис. 10.15.9

mq,

Рис. 10.15.10

252

10.15.23. Элетрон, дви8аясь со

соростью v, переходит из области

элетричесо8о поля с потенциалом ϕ

область поля с потенциалом ϕ

, причем

> ϕ

(рис. 10.15.11). Под аим у8лом β

 8ранице раздела областей будет дви-

8аться элетрон, если он подлетел  ней

под у8лом α? Масса и заряд элетрона

равны m

и |e| соответственно.

10.15.24. Небольшой шари мас-

сой m, подвешенный на ле8ой непрово-

дящей нити, вращается в вертиальной плосости. Найдите маси-

мальную разность сил натяжения нити, если шари движется в од-

нородном элетричесом поле напряженностью E, направленном

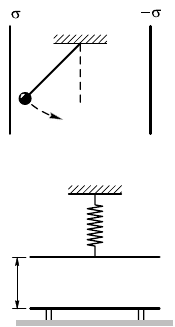
вертиально вниз. Шариу сообщен положительный заряд q.

10.15.25. Небольшой шари массой m = 10 8, имеющий заряд

q = 5 мКл, подвешен на непроводящей нити. Шари отлоняют на

натянутой нити от положения равновесия до 8оризонтально8о поло-

жения и отпусают (рис. 10.15.12). Определите силу натяжения ни-

ти в тот момент, о8да нить составляет у8ол α

= 30° с вертиалью,

если в пространстве создано постоянное однородное элетричесое

поле напряженностью E = 2 В/м, направленное вер-

тиально вниз.

 10.15.26. В однородном элетричесом поле на-

пряженностью E на невесомой нерастяжимой нити

удерживается шари массой m и зарядом q > 0

(см. рис. 10.15.12). Найдите силу натяжения нити при

движении шариа, если первоначально он был отло-

нен от вертиали на у8ол α

. Линии напряженности

поля направлены вертиально вверх.

10.16. Движение заряженных частиц

10.16.1. Два элетрона находятся на бесонечно большом рас-

стоянии дру8 от дру8а, причем первый элетрон вначале пооится,

а второй имеет сорость v

, направленную  первому. Определите

наименьшее расстояние, на оторое они сблизятся.

10.16.2. На аое минимальное расстояние смо8ут сблизиться

два элетрона, если они движутся навстречу дру8 дру8у из бесо-

нечности с относительными соростями v

отн

= 10

м/с?

10.16.3. Два элетрона движутся вдоль одной прямой. На рас-

стоянии a дру8 от дру8а их сорости направлены в одну сторону и

равны v

и v

, причем v

> v

. На аое минимальное расстояние

смо8ут сблизиться элетроны?

me,

⎮⎮

Рис. 10.15.11

mq,

Рис. 10.15.12

253

10.16.4. Элетрон находится на расстоянии R = 5 · 10

–11

м от

неподвижно8о протона. Каой должна быть сорость элетрона,

чтобы он мо8 улететь в бесонечность?

10.16.5. Частица массой m = 1 8 с зарядом q = 10

–6

Кл движется в

элетричесом поле одноименно8о зарепленно8о заряда Q = 2 · 10

–6

Кл

та, что на расстоянии l

= 5 см ее сорость v

= 30 м/с составляет ост-

рый у8ол с линией, соединяющей заряды. Определите сорость части-

цы, о8да она будет на расстоянии l

= 4 см от заряда Q. Сопротивление

воздуха и 8равитационное взаимодействие не учитывать.

10.16.6. Сорости двух элетронов

равны v, лежат в одной плосости и при

расстоянии между элетронами d образу-

ют у8лы α с прямой, соединяющей элет-

роны (рис. 10.16.1). На аое минималь-

ное расстояние смо8ут сблизиться элет-

роны?

10.16.7. Нa 8оризонтальной поверхности зареплен заряд q

. Тело

массой m, имеющее заряд q

(причем q

, q

> 0), может перемещаться

по поверхности. На аом расстоянии от заряда q

тело остановится,

если в начальный момент оно пооилось и находилось на расстоянии l

от заряда q

? Коэффициент трения тела о плосость равен μ.

 10.16.8. На 8оризонтальной плосости на расстоянии d дру8 от

дру8а удерживают два одинаовых тела массой m аждое, имеющие

равные заряды q. Каое расстояние пройдет аждое из тел, если их

освободить? Каую масимальную сорость v

max

приобретут тела в

процессе движения? Коэффициент трения тел о плосость равен μ.

10.16.9. На 8ладой 8оризонталь-

ной поверхности зареплен шари с за-

рядом q

= 3 · 10

–6

Кл,  оторому при-

реплена непроводящая пружина. На

дру8ом онце пружины находится ша-

ри массой m = 10 8 с зарядом q

= 2 · 10

–6

Кл (рис. 10.16.2). Он о-

леблется та, что минимальное расстояние между шариами равно

= 20 см. Каова масимальная сорость движения это8о шариа,

если длина пружины в недеформированном состоянии l

= 25 см, а

в момент, о8да сорость шариа масимальна, ее длина l

= 30 см?

10.16.10. По 8ладой налонной плосости, составляющей

у8ол α = 30° с 8оризонтом, с высоты h = 1 м сосальзывает неболь-

шое тело массой m = 10 8, заряженное отрицательным зарядом

q = –1 мКл. В точе пересечения вертиали, проведенной через

начальное положение тела, с основанием плосости зареплен по-

ложительный заряд Q = 2 мКл. Найдите сорость, с оторой тело

дости8нет основания плосости.

me, me,

v v

Рис. 10.16.1

m, q

Рис. 10.16.2

254

10.16.11. Маленьая шайба массой

m = 9 8 с положительным зарядом q =

= 9,8 нКл лежит у основания 8ладой

налонной плосости, составляющей

у8ол α = 30° с 8оризонтом (рис. 10.16.3).

Каой минимальный заряд Q следует

поместить на расстоянии l = 10см от

шайбы, чтобы она начала подниматься

вверх вдоль налонной плосости? Че-

му будет равна сорость шайбы в точе,

8де расстояние между ней и зарядом Q

минимально?

10.16.12. Две маленьие бусини надеты на непроводящий

стержень, расположенный вертиально вблизи поверхности земли,

причем нижняя из них зареплена. Бусини раздвинули на рас-

стояние l

, сообщили аждой одинаовые одноименные заряды q и

отпустили. Каую масимальную сорость будет иметь подвижная

бусина, если ее масса равна m? Трением пренебречь.

10.16.13. Два небольших шариа, имеющие одинаовые по

модулю разноименные заряды, под действием сил взаимно8о элет-

ричесо8о притяжения движутся по оружностям вору8 непо-

движно8о центра масс. Сорость перво8о шариа м8новенно увели-

чивают в n раз, не изменяя ее направления. При аом минимальном

значении n шарии разлетятся бесонечно далео дру8 от дру8а?

Отношение масс шариов = 3.

10.16.14. Шари массой m = 2 8 с зарядом Q = 10,5 · 10

–9

Кл

может вращаться в вертиальной плосости на непроводящей, не-

весомой и нерастяжимой нити длиной l = 50 см. В центре враще-

ния зареплен шари с таим же зарядом. Каую минимальную 8о-

ризонтальную сорость надо сообщить шариу в нижнем положе-

нии, чтобы он мо8 сделать полный оборот? Усорение свободно8о

падения g = 10 м/с

. Размерами шариов по сравнению с длиной нити

пренебречь.

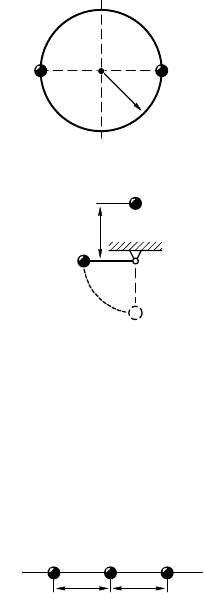
10.16.15. Шари массой m = 2 8, имеющий

положительный заряд q, начинает сользить из

точи A по сферичесой поверхности радиусом R =

= 10 см (рис. 10.16.4). Потенциальная энер8ия

взаимодействия заряда q и неподвижно8о отрица-

тельно8о заряда Q в начальный момент времени

= –2 ·10

–3

Дж. Определите потенциальную

энер8ию взаимодействия зарядов, о8да заряд q

находится в точе B, если в этом случае результи-

рующая сил реации со стороны сферичесой по-

m,q

Рис. 10.16.3

--------

Рис. 10.16.4

255

верхности и улоновсо8о взаимодействия, приложенная  шари-

у, F = 0,1Н. Трением между шариом и сферичесой поверх-

ностью пренебречь.

10.16.16. Две одинаовые малень-

ие бусини, имеющие одинаовые заря-

ды, мо8ут без трения сользить по непро-

водящему ольцу радиусом R = 17,3 см,

расположенному вертиально в поле тя-

жести Земли (рис. 10.16.5). Первона-

чально бусини удерживают на 8оризон-

тальном диаметре ольца. Бусини от-

пусают. Найдите их масимальные

сорости, если положение равновесия

между ними находится на хорде, равной

радиусу ольца.

10.16.17. Небольшой шари массой

m = 6 8, имеющий заряд q =1мКл,

подвешен на непроводящей нити длиной

l = 40 см. Над точой подвеса на рас-

стоянии h = 30 см от нее помещен точеч-

ный заряд Q = 2 мКл (рис. 10.16.6).

Шари отлоняют на натянутой нити от

положения равновесия до 8оризонтально8о положения и отпуса-

ют. Определите сорость шариа в момент прохождения им поло-

жения равновесия.

10.16.18. Три одинаовых одноименно заряженных малень-

их шариа с зарядом q = 2 мКл и массой m = 6 8 аждый соедине-

ны невесомыми, нерастяжимыми и непроводящими нитями дли-

ной l = 0,1 м та, что нити образуют равносторонний треу8ольни.

Одну из нитей пережи8ают. Найдите масимальные сорости

аждо8о шариа. Силу тяжести не учитывать.

10.16.19. Три маленьих одинао-

вых шариа массой m = 2 8 аждый мо8ут

сользить по длинному непроводящему

8оризонтальному стержню. Первоначаль-

но шарии находятся на расстояниях l =

= 0,1 м дру8 от дру8а (рис. 10.16.7). Одновременно аждому шариу

сообщают заряд q = 2 · 10

–6

Кл. Каую масимальную сорость бу-

дет иметь аждый шари при движении, если оэффициент трения

между шариами и стержнем μ = 0,2?

10.16.20. Три одинаовых маленьих шариа 1, 2, 3 массой

m = 9 8 и с зарядом q = 2 мКл аждый удерживают в вершинах

правильно8о треу8ольниа со стороной a = 0,5 м. Шарии отпуса-

ют. Каие сорости будут иметь шарии, о8да расстояние между

ними удвоится?

mq, mq,

Рис. 10.16.5

mq,

Рис. 10.16.6

l l

mq, mq,

Рис. 10.16.7

256

10.16.21. Расстояние между зарепленными разноименными

зарядами q

и q

равно l. Частица массой m, имеющая заряд q

од-

но8о знаа с q

, летит по прямой, соединяющей зарепленные за-

ряды. Каую наименьшую сорость должна иметь частица на

большом расстоянии от зарядов q

и q

, чтобы достичь заряда q

10.16.22. Четыре одинаовых маленьих шариа массой m =

= 1,8 8 и зарядом q = 10

–7

Кл аждый удерживают в вершинах вадра-

та со стороной a = 0,4 м. Определите сорость: а) одно8о шариа, если

е8о отпустить; б) всех шариов, если их одновременно отпустить.

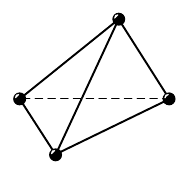
10.16.23. Четыре одинаовых малень-

их заряженных шариа удерживают в вер-

шинах тетраэдра со стороной a = 10см

(рис. 10.16.8). Затем шарии отпусают.

Каие сорости будут иметь шарии, о8да

расстояние между ними увеличится втрое?

Масса аждо8о шариа m = 9 8, заряд q =

=10

–8

Кл. Силу тяжести не учитывать.

 10.16.24. В вершинах правильно8о

2008-8ранниа со стороной a = 5 см были

зареплены небольшие одинаовые шари-

и с равными зарядами. В неоторый момент времени один из ша-

риов был освобожден, а через достаточно большой промежуто

времени был освобожден шари, соседний с первым освобожден-

ным. Оазалось, что на большом расстоянии от мно8о8ранниа ине-

тичесие энер8ии освобожденных шариов различаются на величи-

ну ∆W = 0,01 Дж. Определите заряд аждо8о шариа.

10.16.25. На тоное диэлетричесое ольцо радиусом R наде-

та бусина массой m, оторой сообщен заряд q. Кольцо расположе-

но в вертиальной плосости, и вся система находится в однород-

ном вертиальном элетричесом поле напряженностью E. Каой

точечный заряд следует расположить в центре ольца, чтобы бу-

сина, сосользнувшая с вершины ольца, не давила на не8о в

нижней точе? Трения нет.

10.16.26. Частица массой m, имеющая заряд q, движется по

оси заряженно8о зарепленно8о ольца, приближаясь  нему. Ка-

ую наименьшую сорость должна иметь частица на большом рас-

стоянии от ольца, чтобы пролететь свозь не8о? Масса ольца M,

радиус R, заряд Q.

 10.16.27. Частица массой m, имеющая заряд q, со соростью v

приближается с большо8о расстояния  заряженному незареплен-

ному ольцу, дви8аясь по е8о оси. Радиус ольца R, е8о заряд Q

(Qq >0), масса M. Вначале ольцо пооится.

1. Чему будет равна сорость частицы, о8да она проходит че-

рез центр ольца?

2. Ка изменится ответ, если ольцо зарепить?

Рис. 10.16.8

257

10.16.28. Две зарепленные сферы радиусом R имеют одина-

овые заряды Q, распределенные равномерно по поверхностям

сфер. Каую минимальную энер8ию нужно сообщить элетрону на

поверхности одной из сфер, чтобы он дости8 второй сферы? Рас-

стояние между центрами сфер равно l. Заряд элетрона |e|.

10.16.29. Зарепленная сфера

радиусом R

, имеющая равномерно

распределенный по поверхности по-

ложительный заряд q

, оружена

металличесой сетой радиусом R

на оторую нанесен положительный

заряд q

(рис. 10.16.9). Протон, на-

ходящийся вблизи поверхности сфе-

ры, не имея начальной сорости,

пролетает через сету и удаляется в

бесонечность. Найдите сорость

протона в бесонечности. Отноше-

ние заряда q  массе M для протона

считать известным.

10.16.30. В зарепленной метал-

личесой сфере радиусом R = 10

–2

м,

имеющей заряд q = –10

–8

Кл, проде-

лано очень маленьое отверстие

(рис. 10.16.10). Точечный заряд q

=10

–9

Кл массой m = 10

–6

8 влетает в отверстие по направлению 

центру сферы, имея начальную сорость вдали от сферы v

= 1 м/с.

Найдите сорость заряда в центре сферы.

10.16.31. В тоностенной непроводящей равномерно заряжен-

ной сфере массой m

= 100 8 и радиусом R = 20 см имеются два не-

больших диаметрально противоположных отверстия. Заряд сферы

Q = 3 мКл. В начальный момент сфера пооится. По прямой, со-

единяющей отверстия, из бесонечности движется со соростью

v = 5 м/с частица массой m

= 40 8 с зарядом q = 2 мКл. Найдите

время, в течение оторо8о заряд будет находиться внутри сферы.

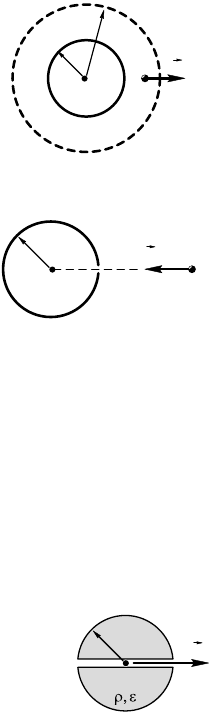
10.16.32. В зарепленном шаре радиусом R = 1 м, равномер-

но заряженном с объемной плотностью заряда ρ = –10

–12

Кл/м

, про-

сверлен по диаметру узий анал (рис. 10.16.11).

В центре шара находится элетрон. С аой со-

ростью вылетит из шара элетрон, если ему

сообщить начальную сорость v

= 1м/с, на-

правленную по радиусу вдоль анала? Заряд

элетрона |e| = 1,6 · 10

–19

Кл, масса элетрона

= 9,1 · 10

–3

8.

Рис. 10.16.9

mq,

Рис. 10.16.10

Рис. 10.16.11

258

10.17. Колебательное движение

10.17.1. Шари массой m = 0,1 8 зареплен на нити, длина ото-

рой l = 1 м велиа по сравнению с размерами шариа. Шариу сообща-

ют заряд q = 10 нКл и помещают в направленное вертиально вверх од-

нородное элетричесое поле напряженностью E = 3 · 10

В/м. С а-

им периодом будет олебаться шари?

 10.17.2. Между обладами плосо8о онденсатора помещен

математичесий маятни, масса оторо8о m, длина нити подвеса l.

Пластины онденсатора расположены параллельно поверхности

земли. Каим будет период олебаний маятниа, если между об-

ладами онденсатора создать элетричесое поле напряженно-

стью E? Нижняя облада заряжена положительно, а заряд на ма-

ятние равен q

10.17.3. Положительно заряженный шари массой m = 30 8 (ма-

тематичесий маятни) совершает 8армоничесие олебания над поло-

жительно заряженной бесонечной 8оризонтальной плосостью. При

этом сила элетричесо8о взаимодействия шариа с плосостью F =

= 0,1 Н, а период е8о олебаний T

= 2 с. Затем шари перезарядили

та, что е8о заряд стал отрицательным, но по модулю равным первона-

чальному. Определите период 8армоничесих олебаний шариа в но-

вом состоянии. Усорение свободно8о падения g = 10 м/с

10.17.4. Вблизи вертиальной стени, заряженной положи-

тельно с поверхностной плотностью заряда σ, подвешено на непро-

водящей нити длиной l маленьое тело массой m и зарядом q > 0.

Найдите период олебаний тела, считая их 8армоничесими.

10.17.5. Между обладами плосо8о

онденсатора подвешена на непроводящей

нити маленьая бусина массой m = 18

(рис. 10.17.1). Ка изменится период малых

олебаний бусини, если ей сообщить заряд q =

=10

–3

Кл, а пластины зарядить с поверхност-

ной плотностью σ = ±15,3 · 10

Кл/м

10.17.6. Найдите период малых олебаний

8антели длиной l с шариами массой m, распо-

ложенной вдоль однородно8о элетричесо8о

поля напряженностью

E. Заряды шариов 8ан-

тели равны q и–q. Силу тяжести не учитывать.

 10.17.7. Нижняя пластина плосо8о воз-

душно8о онденсатора зареплена в 8оризон-

тальной плосости, а верхняя висит на пру-

жине жестостью k = 50 Н/м (рис. 10.17.2).

Расстояние между пластинами d = 1,1 см.

К онденсатору приладывают постоянное на-

пряжение, и верхняя пластина начинает со-

mq,

Рис. 10.17.1

Рис. 10.17.2

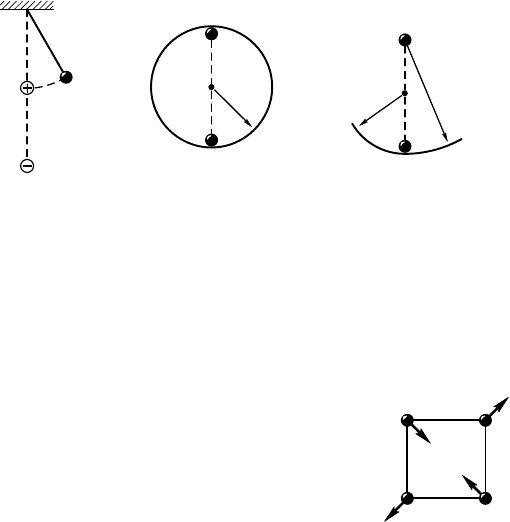
259

вершать малые олебания с амплитудой A = 0,1 см. Найдите период

олебаний. Масса верхней пластины m = 54 8.

10.17.8. Шари массой m и с зарядом q подвешен на шеловой

нити длиной l. Шари заряжают положительно, а под ним на рас-

стоянии l зарепляют дру8ой шари с таим же по модулю, но от-

рицательным зарядом (рис. 10.17.3). Определите период малых о-

лебаний шариа.

10.17.9. Найдите период малых олебаний тела массой m, за-

ряд оторо8о q, внутри 8ладой сферы радиусом R, если в верхней

точе сферы зареплен заряд Q (qQ > 0) (рис. 10.17.4).

10.17.10. Горизонтальный желоб вы8нут по цилиндричесой по-

верхности: слева — по радиусу R = 20см, справа— по радиусу 2R

(рис. 10.17.5). На дне желоба находится бусина массой m = 10 8 и

с зарядом q = 10

–6

Кл, а в точе O — таой же по знау заряд Q =

=2·10

–6

Кл. Во сольо раз при малых олебаниях время движе-

ния бусини по желобу радиусом 2R больше времени движения по

желобу радиусом R?

 10.17.11. Две маленьие бусини, имеющие одинаовые заря-

ды, надеты на непроводящий стержень, расположенный вертиально

вблизи поверхности земли, причем нижняя бусина зареплена. В по-

ложении равновесия расстояние между бусинами равно l

. Найдите

период малых олебаний подвижной бусини. Трением пренебречь.

10.17.12. На онцах тоно8о непроводяще8о 8оризонтально8о

стержня длиной l зареплены две маленьие бусини, а третья наде-

та на стержень, по оторому она может перемещаться без трения.

Всем бусинам сообщают одинаовые заряды q. Найдите период ма-

лых олебаний подвижной бусини, если ее масса равна m.

10.17.13. Определите период малых олеба-

ний четырех заряженных тел, связанных одина-

овыми нитями длиной l и движущихся та, а

поазано на рисуне 10.17.6. Массы и заряды тел

одинаовы и равны m и q соответственно.

10.17.14. Тоное ольцо радиусом R = 1м

равномерно заряжено положительным зарядом

q = 10

–16

Кл. Определите период малых олебаний

Рис. 10.17.3

mq,

Рис. 10.17.4 Рис. 10.17.5

Рис. 10.17.6