Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 53

= S

/A, where A

is the area of wrinkled laminar ﬂame in a streamtube

of cross-sectional area A. The conditions under which an unstretched laminar ﬂame

can provide a valid model for localised zones of heat release in premixed turbulent

combustion were reviewed by several authors, including Peters [55], Poinsot and

Veynante [56], and Driscoll [57], and are often presented in the form of a regimes

diagram such as that shown in Fig. 1.3. The classical perspective assumes that lam-

inar ﬂamelets will persist so long as a laminar ﬂame is thinner than all scales of

turbulence, that is, when the Karlovitz number Ka = τ

/τ

< 1. Thickened ﬂamelets

are assumed to occur whenever Ka ≥ 1. However, much experimental and DNS

evidence [57] now suggests that laminar-like reaction-zone structures can be much

more robust than is implied by the Ka = 1 criterion. An explanation may be found

in studies [58, 59] of individual vortices interacting with laminar ﬂames: Small eddies

are found to be unable to disrupt the ﬂame structure, as they are rapidly dissipated

by the combined effects of viscosity and dilatation. Consequently laminar-like ﬂame

zones persist in much more intense turbulence than was previously thought possi-

ble. However, it must be kept in mind that, however small Ka may be, composition

gradients in the outermost edges of these ﬂame zones will always be inﬂuenced by

turbulent ﬂuctuations. Some models [46, 55] describe these interactions in terms of

a preheat zone that is thickened by turbulence followed by a thin laminar reaction

layer. Another perspective [60] argues that the range of validity of ﬂamelet models

may be extended by including the inﬂuence of stretch on a laminar ﬂame.

Laminar ﬂamelet models can be implemented in several different ways: One

approach [61] is to represent the reaction zones in terms of a laminar ﬂame speed

(with or without allowance for the inﬂuence of strain and curvature) and a ﬂame

surface area or FSD

. The mean chemical source term in the

c equation is then ˙ω

, where I

is a factor to allow for the inﬂuence of ﬂame stretch. Alternatively,

in a level-set or G-equation approach [55], the rate of propagation of a chosen

isosurface is modelled. Another way to apply a laminar ﬂamelet model is to assume

(see Section 2.2 and [62, 63]) that all chemical species mass fractions Y

(x, t) and their

reaction rates ω

(x, t) at given temperature, pressure, and composition are unique

functions of c, determined from the properties of an unstretched laminar ﬂame. This

assumption can be combined with several different alternative mean-reaction-rate

models; for example, in a presumed PDF model (see Chapter 1, Subsection 1.7.2),

the chemical kinetic mechanism allows ˙ω

reaction rates ˙ω

i,F

(c). Then

˙ω



ρ(c)

˙ω

c,F

(c)

(c; x)dc, (2.24)

where

(c; x) is the presumed Favre PDF, and



i,F

(c)

(c; x)dc, (2.25)

where Y

i,F

A more r estrictive but potentially powerful laminar ﬂamelets approach, explored

in the next subsection, is to assume [21, 62] that reaction zones can be replaced with

unstretched laminar ﬂames not only in composition space but also in physical space.

54 Modelling Methods

Laminar ﬂame stretch, which is included in the model of Bradley et al. [ 45 ], is brieﬂy

considered at the end of this section.

2.1.5 A Simple Laminar Flamelet Model

To develop this presumed PDF laminar ﬂamelet analysis we recall from Chapter 1,

Eq. (1.39), that the PDF

P(c

∗

; x) on a chosen internal isosurface c = c

∗

is related to

the surface density function (c

∗

; x)by[64, 65]

(c

∗

; x) =





∂c

∂x



∗



P(c

∗

, x). (2.26)

In the limit of thin weakly wrinkled laminar ﬂamelets, (c

∗

; x) is almost independent

of the choice of the isosurface c

∗

, so l ong as c

∗

is not too close to zero or unity and

is identiﬁed as the FSD

(x). The progress-variable gradient at a point c = c

∗

in a

steady, unstretched laminar ﬂame is a function of c

∗





∂c

∂x



∗





dη



. (2.27)

Although this assumption may be valid in the interior of the reaction zone, where

the composition gradients are large, it must become less accurate at the edges of this

zone. It follows from Eq. (2.27) that the interior part of the PDF

P(c; x)ofEq.(2.4)

as a function of c is [41, 62]



dη



−1

, (2.28)

where C

is a normalising factor given by

1 = C



−

(

dc/dη

)

= C



max

min

dη.

Here 0

and 1

−

represent the limits within which (c; x) is to be assumed constant and

η = η

min

and η

max

are the corresponding values of η. It then follows that C

= 1/η,

where η = η

max

− η

min

is a measure of the laminar ﬂame thickness.

The ﬂamelets contribution to the Reynolds mean of any property ϕ can then be

found as

ϕ(x) − α(x)ϕ

− β(x)ϕ

= γ(x)



−

(c)f

(c)dc

= γ(x)



−

(c)

(

dc/dη

)

(c)

γ(x)

η



max

min

[c(η)] dη, (2.29)

where the integral can be determined from a laminar ﬂame calculation.

This analysis was used in Ref. [18] to model ﬂamelet contributions to the pressure

gradient co-variances in the s econd-moment transport equations; see Eq. (2.18). The

co-variances were found to play an important role in the closure of these equations,

so the successful prediction of second-moment quantities, illustrated in Figs. 2.4

and 2.5, provides support for the validity of the approach. We now illustrate the

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 55

application of the analysis by using it to derive simple laminar ﬂamelet expressions

for the mean reaction rate and by recovering the relationship, Eq. (2.9), between this

and the mean scalar dissipation. The mean reaction rate can be expressed in several

different ways, the ﬁrst of which is

˙ω

= γC



max

min

˙ω

[c(η)] dη =

η

, (2.30)

where the c equation for an unstretched laminar ﬂame is used to evaluate the integral,

assuming η

max

→∞and η

min

→−∞.

To evaluate this equation, the burning-mode (BM) probability γ can be related

to the variance



2

by use of the PDF of Eq. (2.4) to ﬁnd expressions for

c and



2

terms of α, β, and γ and recalling that α + β + γ = 1. The result is

γ =

η

c(1 −

(1 + τ

c)δ

∗

, (2.31)

where (x) is a variance parameter deﬁned as

 = 1 −



2

c(1 −

which may be predicted from a solution to the transport equation for



2

. We have

  1 in the thin-ﬂamelets limit in which ˜γ  1 and  → 1 if the variance approaches

zero. It may be seen that  = O(γ) = O(1/Da) in the present analysis. Also δ

∗



max

min

c(1 − c)/(1 + τc)dη is another measure of the laminar ﬂame thickness, which

reaches a constant value as η

max

and η

min

approach ±∞. Note that γ ∼ η because,

in this simple model, the reaction-zone probability increases when the laminar ﬂame

limits η

max

and η

min

are extended.

It follows from Eqs. (2.30) and (2.31) that

˙ω



c(1 −

(1 + τ

c)δ

∗

, (2.32)

which removes the apparent sensitivity of

˙ω

in Eq. (2.30) to the choice of η

max

and

min

. This expression can be rewritten in terms of the generalised FSD 

. The SDF

of an isosurface c = c

∗

(c

∗

) =



∂c

∂x

||c

∗



∗

) =

η

, (2.33)

and, as assumed earlier, this is independent of c

∗

. It follows that the generalised

FSD is



≡



(c

∗

)dc

∗

=  =

η



c(1 −

(1 + τ

c)δ

∗

. (2.34)

An alternative way of presenting this laminar ﬂamelet mean-reaction-rate

model, in terms of chemical kinetic parameters rather than laminar ﬂame properties,

can be obtained from

˙ω

= γ



−

˙ω

(c)f

(c)dc. (2.35)

If we now introduce a dimensionless reaction-rate function 

/ρB, where B

is a characteristic reaction-rate constant with dimension (time)

−1

, and substitute f

56 Modelling Methods

100

0.1

0.01

0.0

PDF

0.2 0.4

(a) (b) (c)

0.6 0.8 1.0

1000

100

0.1

0.01

0.0

PDF

0.2 0.4 0.6 0.8 1.0

100

0.1

0.01

0.0

PDF

0.2 0.4

ccc

0.6 0.8 1.0

Beta

DNS

c = 0.25

Flamelet

Double delta

c = 0.51

c = 0.74

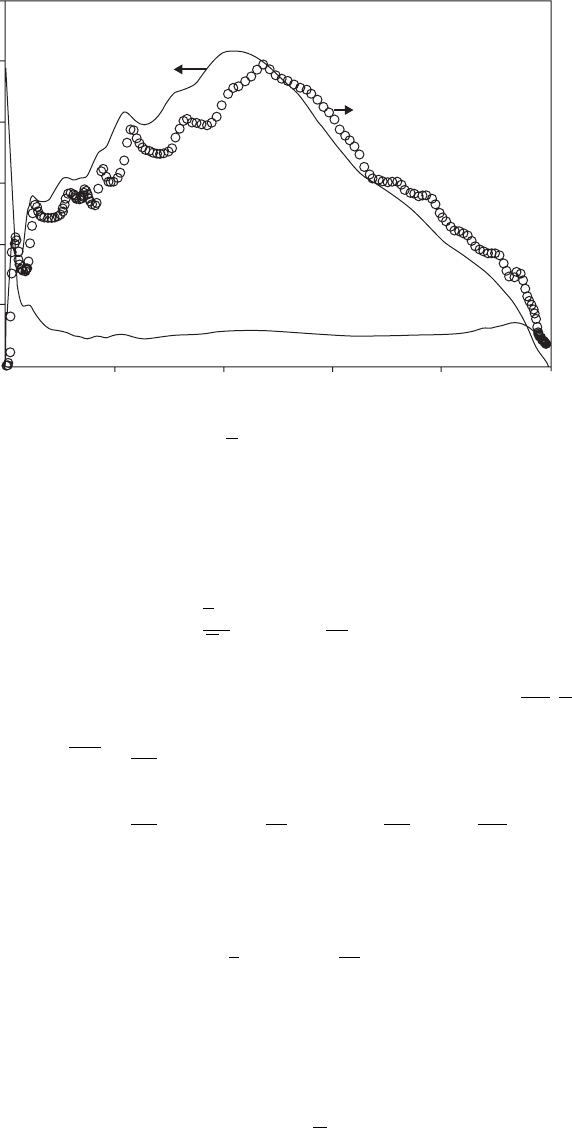
Figure 2.6. Laminar ﬂamelet PDF (heavy line), beta function PDF (light line), and twin-delta

PDF (triangles), compared with DNS data of Rutland and Cant [43] (data points); from Bray

et al. [41].

from Eq. (2.28) and γ from Eq. (2.31), we ﬁnd [41]

˙ω

=  ρ

c(1 −

c)I

B, (2.36)

where

∗



max

min



(η)

1 + τc(η)

dη

is a constant, related to the assumed global reaction-rate mechanism, whose value can

be calculated from a laminar ﬂame solution. Comparing Eqs. (2.36) with the earlier

mean-rate expression of Eq. (2.30) and using Eq. (2.31), we ﬁnd that I

B = S

/δ

∗

Equation (2.36) shows the mean reaction rate to be the product of a turbulent

mixing factor

c(1 −

c) and a reaction-rate factor I

B. Note that, if the order

of magnitude  = O(γ) = O(1/Da) were to be replaced with an ad hoc model of

the form  = constant/Da, the chemical time scale in Eq. (2.36) would cancel, the

turbulence time

k/˜ would control reaction, and an eddy break-up (EBu) mean-

reaction-rate expression would be recovered. However, experience shows this to be

incorrect, as the mean rate depends on both characteristic s cales.

It was shown in [41] that, in the limit γ  1, other presumed PDF shapes

(c; x)

lead to exactly the same mean-reaction-rate expression as Eq. (2.36), but with the

constant I

replaced with a constant I

whose magnitude depends on the reaction-

rate expression and the shape of the PDF

(c; x). It is also shown in [41] that I

and I

approach constant values when the ﬂamelet limits η

min

and η

max

approach

±∞. The ﬂamelet PDF is shown to give the best agreement with the DNS data of

Rutland and Cant [43], as shown in Fig. 2.6, and to provide an excellent match to

the mean heat release rate from the DNS; see Fig. 2.7. By way of contrast, a beta

function PDF gives a mean rate 2.4 times as large as that required to match the DNS,

whereas a double delta leads to a rate that is 8.6 times too large.

We turn now to the scalar dissipation ˜

, which must be modelled in order to

determine  from the



2

equation. The instantaneous scalar dissipation function is

ρN = ρ

(

∂c/∂x

)(

∂c/∂x

)

if it is assumed that ρD = ρ

. We further assume that

the gradient within a ﬂamelet is large in comparison with mean property gradients,

and

ρN can then be equated to ρ

, which is the dissipation term in the transport

equation for the variance



2

. Thus

ρ˜

 ρN = ρ

η



−



dη



dc. (2.37)

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 57

1.2

1.0

0.8

0.6

0.4

0.2

0.0

Model

Magnitude

DNS

0.0 0.2 0.4 0.6

0.8 1.0

Figure 2.7. Mean heat release rate ω

/ and  vs

c: Predictions compared with DNS data of

Rutland and Cant [43] (data points). From Bray et al. [41].

Equations (2.30) and (2.37) both contain the BM probability γ, which can be

eliminated by forming the ratio of Eqs. (2.30) and (2.37). If we introduce the laminar

ﬂame thickness δ = D

, we ﬁnd

ρ˜

˙ω

= δ



−



dη



dc, (2.38)

which resembles the reaction–dissipation relationship of Eq. (2.9). To demonstrate

that these two expressions are compatible, we may calculate C

≡ c ˙ω

/ ˙ω

from

c ˙ω

η



max

min

c ˙ω

dη

η



max

min

dη

dη − ρ

η



max

min

dη

dη,

where the c equation for an unstretched laminar ﬂame has been used. Evaluation of

the integrals then shows that C

in this ﬂamelet model is a constant, given by

−

= δ



−



dη



dc, (2.39)

and substitution of this into Eq. (2.38) allows Eq. (2.9) to be recovered.

The ﬂamelet mean-reaction-rate expressions of Eqs. (2.32) and (2.36) contain

the chemical time scale δ

∗

= 1/I

B, but characteristic turbulence scales can enter

the present description only by means of (x). This quantity can be determined from a

solution of the transport equation for the variance



2

, which determines the balance

between the reactive part γ(x)ofthePDF

P(c; x) and the non-reactive components

α(x) and β(x). Although an expression for the scalar dissipation ˜

in this equation

may be obtained because of Eq. (2.36) and the reaction–dissipation expression,

58 Modelling Methods

Eq. (2.9), with ˜

(x) expressed in terms of



2

, it does not satisfy the requirement that

all terms in the variance equation must vanish as



2

→ 0. Consequently a model

must be provided for the O(γ) correction to Eq. (2.9), which may be viewed as a

representation of the inﬂuence of turbulent ﬂuctuations on the progress-variable

gradient at the edges of the thin reaction zone. One such model, [32], meets this

‘realisability’ requirement by ensuring that ˜

approaches the classical non-reactive

ﬂow expression, ˜

= C





2

˜/

k, in the limit Da  1, and goes to Eq. (2.9) only when

Da  1. Such models are conceptually related to that of Anand and Pope [ 66 ], who

added a classical turbulence contribution to the conditional scalar dissipation in

their laminar ﬂamelet closure of the transport equation for the J-PDF of velocity

and progress variable in premixed combustion. A consequence of the additional

term in the present problem is that ˜

(x) t hen depends on both sets of characteristic

scales. It may be seen from Eqs. (2.32) and (2.36) that the mean reaction rate is

extremely sensitive to the predicted value of



2

; for example, if  = 0.01, a reduction

of 0.5% in



2

can reduce ˜

and ω

by 50%. The fact that the



2

equation at large

Damk

ohler numbers is essentially a balance between scalar dissipation and reaction

effects suggests a sensitivity of 

and the mean heat release rate to the chosen scalar

dissipation model; see Section 2.3.

An aim of model development for premixed turbulent combustion must be to

derive models that are applicable in a wider range of burning regimes, and laminar

ﬂamelet combustion should be included within this range. Although the present

model is greatly simpliﬁed, it does capture important features of the ﬂamelet heat

release process. It provides a straightforward and tested route to the prediction of

ﬂamelet contributions to the closure of terms such as pressure gradient co-variances

[18]. As shown in Fig. 2.8, combustion ﬂow-ﬁeld predictions [32] using the ﬂamelet

model agree well with experimental data. The separation of mean heat release rate

expression (2.36) into the product of a turbulent mixing factor and a chemical kinetic

factor permits the inﬂuence of the shape of the interior PDF f (c; x) to be quantiﬁed

[41] and has recently been extended [27] to include more complex chemical kinetic

mechanisms.

Finally, the theoretical framework previously presented to describe burning in

terms of assumed unstretched laminar ﬂamelets will be adapted to make qualitative

assessments of the inﬂuence on the mean burning rate of, ﬁrst, laminar ﬂame stretch,

and then a thickening of the laminar ﬂame preheat zone.

STRETCHED LAMINAR FLAMELETS. Bradley et al. [45, 67] describe a second-moment,

stretched laminar ﬂamelet model in which the heat release rate is obtained

in the form ˙ω

(c, K) ≈ ˙ω

(c, K = 0)f (K) from laminar ﬂame calculations, where

K = (u

rms

/λ)(δ/S

) is the Karlovitz stretch factor, λ is the Taylor microscale of tur-

bulence, and f (K) is a correction factor for the inﬂuence of stretch. The mean rate

˙ω

is obtained by multiplying this rate expression by the JPDF P(c, K) and integrating

twice. Taking

P(c, K) = P(c)P(K), they ﬁnd

˙ω

= P



˙ω(c, K = 0)P(c)dc,

where



max

min

f (K)P(K)dK.

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 59

1.0

0.8

0.6

0.4

0.2

0.0

–0.2

–0.4

–0.6

–0.8

–1.0

0.0 0.2 0.4 0.6 0.8 1.0

ε/ε (0)

Figure 2.8. Flamelet predictions [32] (lines) compared with the experimental data of Li et al.

[34] (data points), where W = ˜w(˜z), ˜z = z/d. From Bray et al. [32].

It may be seen that the mean heat release r ate is modelled as the product of a

probability P

that the stretch rate can sustain a ﬂamelet and a mean heat release

rate, calculated in the absence of stretch effects. Bradley et al. [45] assume a beta

function PDF

P(c; x). If we repeat this analysis, replacing the beta function with our

unstretched ﬂamelet PDF, we obtain

˙ω

= P



c(1 −

(1 + τ

∗

, (2.40)

where Eq. (2.32) has been used and S

and δ

∗

are to be evaluated with K = 0. Bradley

et al. [67] calculate P

as a function of K, with Markstein number Ma as a parameter;

with Ma > 0, they ﬁnd it to decrease monotonically with K but, when Ma < 0, P

can

increase with increasing K. This analysis suggests that our simple laminar ﬂamelet

model can be adapted to include the inﬂuence of stretched laminar ﬂames with

Le ≈ 1 simply by including the ﬂamelet burning probability P

, as illustrated in

Eq. (2.40).

THICKENED PREHEAT ZONE. Here we demonstrate that, as expected on physical

grounds, a thickening of the preheat zone in this model will not modify the predicted

mean heat release rate so long as the thickening is conﬁned to a non-reactive portion

of the ﬂamelet. The internal PDF of Eq. (2.28) is modiﬁed as follows: The progress-

variable gradient in a non-reactive portion of the preheat zone where 0 ≤ c ≤ c

∗

assumedtobe1/ϑ times that in a laminar ﬂame, where ϑ ≥ 1; for c

∗

≤ c ≤ 1, the

gradient is that of a laminar ﬂame. Then the constant C

of Eq. (2.28)is

η

≡

ϑ(η

∗

− η

min

) + (η

max

− η

∗

)

, (2.41)

60 Modelling Methods

where η

∗

corresponds to c

∗

, and it follows from Eq. (2.30) that

˙ω

= γ



˙ω

= γC





max

min

˙ω

dη + (ϑ − 1)



∗

min

˙ω

dη



= γC



max

min

˙ω

dη

γρ

η

However, in the thin-ﬂamelets r egime, the ﬂamelet burning probability γ is directly

proportional to the ﬂamelet thickness η

= ϑ(η

∗

− η

min

) + (η

max

− η

∗

), so the in-

ﬂuence of the thickening parameter ϑ cancels from this equation.

In classical descriptions of a laminar ﬂame [68], in terms of an inert preheat layer

followed by a thin reaction layer, the rate of reaction is governed by the molecular-

transport ﬂux from the preheat zone to the reaction layer. I t follows that a thickening

of a part of the preheat zone will not inﬂuence the reaction unless the gradient at

the boundary between the two layers is modiﬁed.

2.1.6 Conclusions

The BML model considers a burning zone formed by one or more thin wrinkled

ﬂame surfaces, identiﬁes ‘turbulence’ production and scalar ﬂux changes that are due

to intermittency between reactants and combustion products, and provides models

to describe these processes. In this subsection we have assumed the wrinkled ﬂame

surface to be adequately represented by an unstretched laminar ﬂame and shown that

the U-shaped interior PDF f (c) is then proportional to the reciprocal of the known

laminar ﬂame gradient dc/dη. Simple algebraic expressions for the mean reaction

rate, proportional to the scalar variance quantity , then follow. To calculate ,the

variance



2

must ﬁrst be determined by closing and solving the ﬁrst of Eqs. (2.3).

Closure of this equation requires a model for the scalar dissipation ˜ε

, and such

models are discussed at length in Section 2.3. Other models, involving a more detailed

description of the interaction between combustion and turbulent ﬂow than has been

presented here, are described in the following pages.

2.2 Flame Surface Density and the G Equation

By L. Vervisch, V. Moureau, P. Domingo, and D. Veynante

FSD and the ﬁeld equation (or G equation) are fundamental tools of premixed

turbulent combustion modelling [55, 56, 69, 70]. They have been intensively studied

in RANS [71–74 ], LES [75–81], and DNS [82–86] contexts and also in experiments

[87, 88].

The FSD and G equation were introduced in combustion mainly for two reasons.

The ﬁrst comes from the direct observation of ﬂames: The reactive fronts behave

as more-or-less convoluted surfaces separating fresh and burnt gases. The second

2.2 Flame Surface Density and the G Equation 61

is related to the discussion in earlier sections of the molecular-diffusion-controlled

character of combustion: According to Fick’s law, molecular diffusion depends on

species gradients developing between isoconcentration surfaces, and the knowledge

of the properties of these surfaces is thus a basic ingredient of turbulent combustion

modelling to which detailed chemical kinetic information can readily be added.

This section reports on the basis of FSD and ﬁeld equation or G equation. The

interlinks between these approaches and the PDF formalism are also discussed in

the context of the introduction of tabulated detailed chemistry in the numerical

simulation of ﬂames.

2.2.1 Flame Surface Density

BASIS OF FSD. Scalar surfaces in turbulent ﬂows are non-planar 2D objects evolving

in time, which are not easy to comprehend directly: The density of isosurface per

unit volume, , was then introduced as an Eulerian quantity [89] deﬁned at every

point in the ﬂow as

(ϕ

∗

; x, t) = lim

δV →0

∗

δV

, (2.42)

to denote the limit, for a measuring volume δV that goes to zero, of the ratio between

∗

, the area of the iso-ϕ

∗

scalar surface, and the volume δV centred at x.

Considering a small volume dV

∗

= A

∗

dξ, built over the A

∗

surface from a

displacement dξ = ξ

− ξ

−

in the direction normal to the surface and centred on

the surface, with ϕ(ξ

, t) = ϕ

∗

+ dϕ/2 and ϕ(ξ

−

, t) = ϕ

∗

− dϕ/2, the probability of

ﬁnding ϕ = ϕ

∗

at x maybewrittenas

P(ϕ

∗

; x, t)dϕ = lim

δV →0

∗

δV

, (2.43)

where

P(ϕ

∗

; x, t)isthePDFofϕ

∗

. This PDF can be deﬁned here in both RANS [90–

92] and LES [93] frameworks. The combination of relations (2.42) and (2.43) yields

(ϕ

∗

; x, t) = P(ϕ

∗

; x, t)G(ϕ

∗

), (2.44)

where G(ϕ

∗

) ≡



dϕ/dξ | ϕ = ϕ

∗



is the conditional mean in RANS, or the conditional

ﬁltered value in LES, of the scalar gradient estimated for ϕ = ϕ

∗

. This relation may

be derived in a more formal way by considering the integral over the volume V of

the ﬁne-grained PDF δ[ϕ

∗

− ϕ(x, t)] [90], leading to the  deﬁnition [94, 95]:

(ϕ

∗

; x, t) = P(ϕ

∗

; x, t)G(ϕ

∗

). (2.45)

From here onwards, G(ϕ

∗

) ≡



|dϕ/dx

||ϕ = ϕ

∗



. Relation (2.45) indicates that the

FSD is a conditional moment of

P(ϕ

∗

,γ

∗

; x, t), the joint scalar, scalar-gradient PDF:

(ϕ

∗

; x, t) =



∞

∗

P(ϕ

∗

,γ

∗

; x, t)dγ

∗

, (2.46)

where γ

∗

is the magnitude of the scalar gradient. With this deﬁnition, (ϕ

∗

; x, t)

features similarities with conditional moment closure (CMC) [96, 97], also focussing

on the behaviour of thermochemical variables (species concentrations, enthalpy) for

given isoscalar values.

62 Modelling Methods

To avoid focussing on a single isoscalar surface, a generalised FSD was also

introduced by integration through the ﬂame [70]:

(x, t) =



(ϕ

∗

; x, t)dϕ

∗

= |∇ϕ|. (2.47)

Surface densities are then all related to scalar gradients and provide direct informa-

tion on the scalar ﬁeld topology.

If ϕ denotes a premixed ﬂame progress variable used to tabulate chemistry [98–

101] then the averaged (RANS) or ﬁltered (LES) burning rate

˙ω

required to simu-

late premixed ﬂame propagation may be written with Eq. (2.45)as

˙ω



˙ω(ϕ

∗

)P(ϕ

∗

)dϕ

∗



1−



˙ω(ϕ

∗

)

(ϕ

∗

; x, t)

G(ϕ

∗

)

dϕ

∗

, (2.48)

where ˙ω(ϕ

∗

) denotes the tabulated chemical source that vanishes for ϕ → 0 and ϕ →

1, so that the integral can be completed in the range ϕ

∗

∈ [, 1 − ], where  is a small

number avoiding the s ingularity appearing when |∇ϕ|→0. Relation (2.48) shows

that the FSD and the conditional mean scalar gradient are fundamental components

of burning rates in both RANS and LES.

The surface density evolves in accordance with the scalar equation controlling

the iso-ϕ

∗

∂ρϕ

∂t

∂ρu

∂x

∂

∂x





ρD

∂ϕ

∂x





+ ˙ω

, (2.49)

where ρ is the mass density, u is the velocity vector, and D

is the molecular-diffusion

coefﬁcient of ϕ assuming Fick’s law. In a reference frame attached to the thin-ﬂame

front, with ξ as the direction normal to the reaction zone, relation (2.49) becomes

∂ρϕ

∂t

∂ρu

∂ξ

∂

∂ξ



ρD

∂ϕ

∂ξ



+ ˙ω

−

, (2.50)

where

is a stretch leakage term that cumulates budgets of ﬂuxes occuring along

the ﬂame surface and is thus representative of transverse convection and diffusion

resulting from straining and curvature of the ﬂamelet surface. The case of a freely

propagating 1-D unstrained premixed ﬂame corresponds to

= 0. For such an

unstrained and steadily propagating ﬂame, the integration across the reaction zone of

the scalar budget with boundary conditions ϕ(−∞) = 0, ϕ(+∞) = 1, and ∂ϕ/∂ξ = 0

at ±∞ gives



+∞

−∞

˙ω

(ξ)dξ = ρ

, (2.51)

where ρ

is the fresh gas mass density and S

is the burning velocity. In thin re-

action zones, the iso-ϕ

∗

surfaces stay almost parallel and  weakly depends on ϕ

∗

;

relations (2.48) and (2.51) provide

˙ω



1−



˙ω(ϕ

∗

)



G(ϕ

∗

)

dϕ

∗

= 



1−



˙ω(ϕ

∗

)

G(ϕ

∗

)

dϕ

∗

= 



+∞

−∞

˙ω

(ξ)dξ = ρ

,

(2.52)

where it is assumed that G(ϕ) =|dϕ/dξ| because the gradient measured through

the laminar ﬂame is a good approximation to the conditional mean gradient in the