Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames
Подождите немного. Документ загружается.

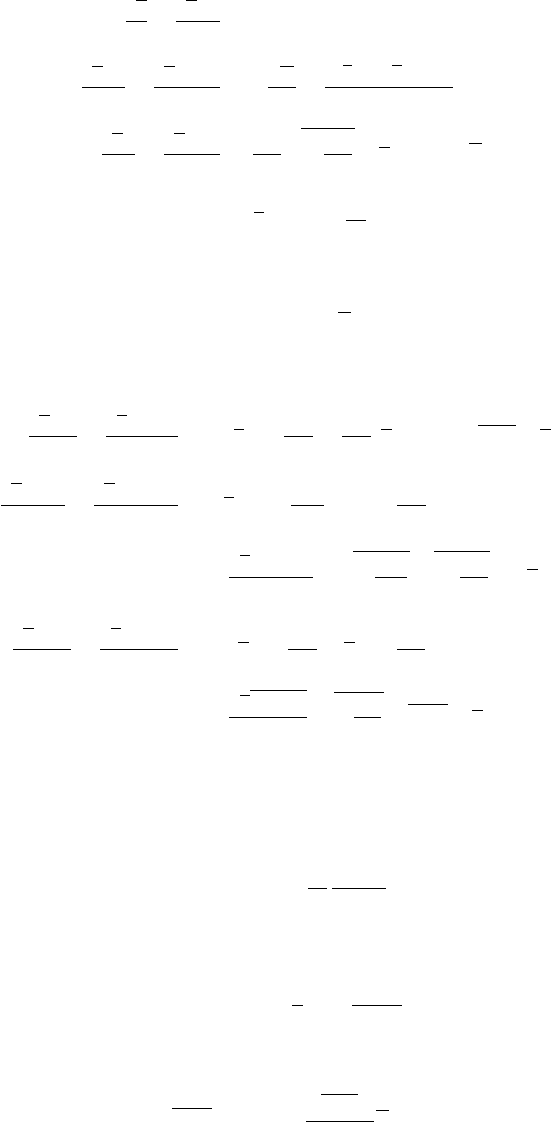
2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 43
Reynolds number, with a Lewis number Le = 1, are
∂
ρ
∂t
+
∂
ρ ˜u
k
∂x
k
= 0,
∂
ρ ˜u
∂t
+
∂
ρ ˜u
k
˜u
∂x
k
=−
∂
p
∂x
+
∂(
τ
k
− ρ
u
k
u
)
∂x
k
,
∂
ρ
˜
c
∂t
+
∂
ρ ˜u
k
˜
c
∂x
k
=
∂
∂x
k
ρν
∂c
∂x
k
− ρ
u
k
c
+
˙ω
c
, (2.2)
where the molecular transport terms
τ
k
and ρν
∂c
∂x
k
are negligible at high Reynolds
numbers, except near solid walls [13]. Buoyancy effects are assumed negligible here,
but were treated in a BML analysis by Libby [14], whose predictions were subse-
quently confirmed by direct numerical simulation (DNS) [15]. Closure assumptions
are required for the mean chemical source term
˙ω
c
together with the Reynolds stress
components
u
u
k
and Reynolds flux components
u
k
c
, which are obtained from the
second-moment equations:
∂
ρ
c
2
∂t
+
∂
ρ ˜u
k
c
2
∂x
k
=−2ρ
u
k
c
∂
˜
c
∂x
k
−
∂
∂x
k
(ρ
u
k
c
2
) + 2c
˙ω
c
−ρ˜
c
,
∂
ρ
u
u
m
∂t
+
∂
ρ ˜u
k
u
u
m
∂x
k
=−ρ
u
k
u
∂ ˜u
m
∂x
k
+
u
k
u
m
∂ ˜u
∂x
k
−
∂
ρ
u
k
u
u
m
∂x
k
−
u
∂p
∂x
m
+ u
m
∂p
∂x
−
ρ˜ε
m
,
∂
ρ
u
c
∂t
+
∂
ρ ˜u
k
u
c
∂x
k
=−
ρ
u
k
c
∂ ˜u
∂x
k
+ ρ
u
k
u
∂
˜
c
∂x
k
−
∂
ρu
k
u
c
∂x
k
− c
∂p
∂x
+ u
˙ω
c
− ρ˜ε
c
. (2.3)
Here the closure requirements include third-moment turbulent transport terms,
which can be approximated by gradient transport expressions of varying degrees of
complexity [11], the simplest of which is [9]
u
k
u
u
m
=−C
s
k
2
ε
∂
u
u
m
∂x
k
,
where C
s
is a constant. Alternatively [16],
u
k
u
u
m
=−C
s
k
ε
u
m
u
n
∂
u
k
u
l
∂x
n
,
where C
s
0.25. The velocity–reaction-rate co-variance is modelled as
u
˙ω
c
= (A −
˜
c)
u
c
˜
c(1 −
˜
c)
˙ω
c
,
44 Modelling Methods
P
c
*
1 – c
*
1
c
0
α
β
γ
Figure 2.1. Sketch of the PDF P(c; x)ofEq.(2.4).
where A is a constant, normally taken to be 0.83. The dissipation terms in the
Reynolds stress and Reynolds flux equations are assumed [11]tobe
ρ˜ε
m
=
2
3
ρ˜εδ
m
+ κ
2
u
c
u
m
c
[
˜
c(1 −
˜
c)]
2
˙ω
c
; ρ˜ε
c
= κ
1
u
c
˜
c(1 −
˜
c)
˙ω
c
,
where [7] κ
1
0.85 and κ
2
0.25 are constants (but see [17], in which a more general
model is proposed). The important scalar dissipation term
ρ˜
c
= D(∂c/∂x
k
)
2
in the
variance equation and the pressure gradient co-variances
c
∂p
/∂x
k
and u
∂p
/∂x
k
,
which are known to play an essential role in models for non-reactive flows, are
discussed later. Finally, an essentially empirical transport equation is required for
the viscous dissipation ˜ε;seeEq.(1.24) in Chapter 1.
(3) PROBABILITY DENSITY FUNCTION. The reacting flow field is partitioned [18]
into three categories: reactants,forwhich0≤ c ≤ c
∗
, reaction zones,forwhich
c
∗
≤ c(x, t) ≤ (1 − c
∗
), and combustion products,forwhich(1− c
∗
) ≤ c ≤ 1, whose
probabilities are denoted by α(x), γ(x), and β(x), respectively, with α + β + γ = 1,
see Fig. 2.1. In the limit c
∗
→ 0, the Reynolds-averaging PDF of c can be written as
P(c; x) = αδ(c) + βδ(1 − c) + γ [H(0) − H(1)] f (c; x), (2.4)
where the Dirac delta functions δ(c) and δ(1 − c) represent reactants and products,
respectively. Also, H is the Heaviside function, f (c; x)istheinternal part of the PDF
P(c; x), and
1
0
f (c; x)dc = 1.

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 45
In the thin-flame limit with Da 1 we have γ 1. No assumption is required at
this point as to whether or not the reaction zone is to be approximated as a laminar
flame.
It is sometimes convenient to define a Favre or mass-weighted PDF, equivalent
to Eq. (2.4) and related to
P by
˜
P(c; x) = ρ(c)/ρP(c; x). Then
˜
P(c; x) = ˜αδ(c) +
˜
βδ(1 − c) + ˜γ [H(0) − H(1)]
˜
f (c; x), (2.5)
so that the Favre mean of any thermochemical variable ϕ(x, t)is
˜ϕ(x) =
1
0
ϕ(x, t)
˜
P(c; x)dc.
It can be shown, using the relationship between
˜
P and
P together with the normali-
sations of f (c) and
˜
f (c), that the two sets of variables are related by
α = ˜α
ρ
ρ
u
,β=
˜
β
ρ
ρ
P
,
γ = ˜γ
1−c
∗
c
∗
ρ
ρ(c)
˜
f (c)dc, f (c) =
ρ
ρ
˜
f (c)
1−c
∗
c
∗
(ρ/ρ)
˜
f (c)dc
.
Continuing in terms of the Reynolds PDF
P of Eq. (2.4), the Reynolds mean of
ϕ is
ϕ(x, t) =
1
0
ϕ(x, t)P(c; x)dc = (1 − c)ϕ
R
+ cϕ
P
+ O(γ), (2.6)
where ϕ
R
and ϕ
P
are t he values of ϕ in reactants and products, respectively. These
terms represent the effects of intermittency between reactants and products, as the
thin-flame surface moves past the location x. Because ˙ω
c
(x, t) is zero everywhere
outside the reaction zones, its mean value,
˙ω
c
(x) = γ(x)
1−c
∗
c
∗
˙ω
c
f (c; x)dc, (2.7)
is proportional to γ. If the turbulent transport terms in the
˜
c transport equation,
Eq. (2.2), are estimated to be O(ρ
u
/τ
T
), whereas ˙ω
c
is O(γρ
u
/τ
L
), then, if ˙ω
c
is to be
of a magnitude similar to that of the transport terms, it follows that γ = O(1/Da).
Consequently, when Da 1, γ(x, t) 1, and Eq. (2.6) shows that, for all properties
other than those like ˙ω
c
(c), which are zero in reactants and products, ˜ϕ can be very
simply approximated in terms of ϕ
R
and ϕ
P
. We also have
ρ =
ρ
u
1 + τ
˜
c
; α =
1 −
˜
c
1 + τ
˜
c
+ O(γ); β =
(1 + τ)
˜
c
1 + τ
˜
c
+ O(γ).
The first of these equations is exact. The Favre variance of c is given by
ρ
c
2
= αρ
u
˜
c
2
+ βρ
P
(1 −
˜
c
2
) + γ
1−c
∗
c
∗
ρ(c −
˜
c)
2
˜
f dc
=
ρ
˜
c(1 −
˜
c) + O(γ), (2.8)
when c
∗
1. It follows that, when γ 1, the variance transport equation is reduced
to a second transport equation for the Favre mean
˜
c. The reconciliation of these

46 Modelling Methods
P(u, c; x)
P
0
(u, 0; x)
u
c
1
0
P
1
(u, 1; x)
u
p
(x)
u(x)
c(x)
u
r
(x)
~
~
Figure 2.2. Sketch of JPDF P(c, u
k
; x).
two transport equations leads [19] to the following important ‘reaction–dissipation’
relationship, which has been confirmed by analysis of DNS data [20], namely,
˙ω
c
=
2
2C
m
− 1
ρ˜
c
+ O(γ), (2.9)
as has been noted in Eq. (1.35). The scalar dissipation ˜
c
can be interpreted as the
reciprocal of a local time scale for molecular transport, and Eq. (2.9) shows the mean
rate of heat release to be linked to the rate at which molecular processes transport
heat and reactive species between reactants and products. With γ 1, both of these
processes occur in the thin reactive–diffusive interfaces separating reactants from
products. It may be seen that, if
˙ω
c
is modelled,
c
can be found from Eq. (2.9), and
vice versa. The modelling of
c
is explored in Section 2.3.
The partitioning illustrated in Eq. (2.6) can be extended [21] to the joint PDF
(JPDF) of a velocity component u
k
(x, t) and the progress variable c(x, t):
P(c, u
k
; x) = αδ(c)f
R
(u
k
; x) + βδ(1 − c)f
P
(u
k
; x)
+γ [H(0) − H(1)] f
F
(c, u
k
; x), (2.10)
as illustrated in Fig. 2.2. Conditional mean velocities in reactants and products can
then be defined from
α
u
k,R
(x) =
c∗
0
∞
−∞
u
k
(x, t)P(c, u
k
; x)du
k
dc,
β
u
k,P
(x) =
1
1−c∗
∞
−∞
u
k
(x, t)P(c, u
k
; x)du
k
dc, (2.11)
where c
∗
→ 0 and it follows that
˜u
k
= (1 −
˜
c)u
k,R
+
˜
cu
k,P
+ O(γ). (2.12)
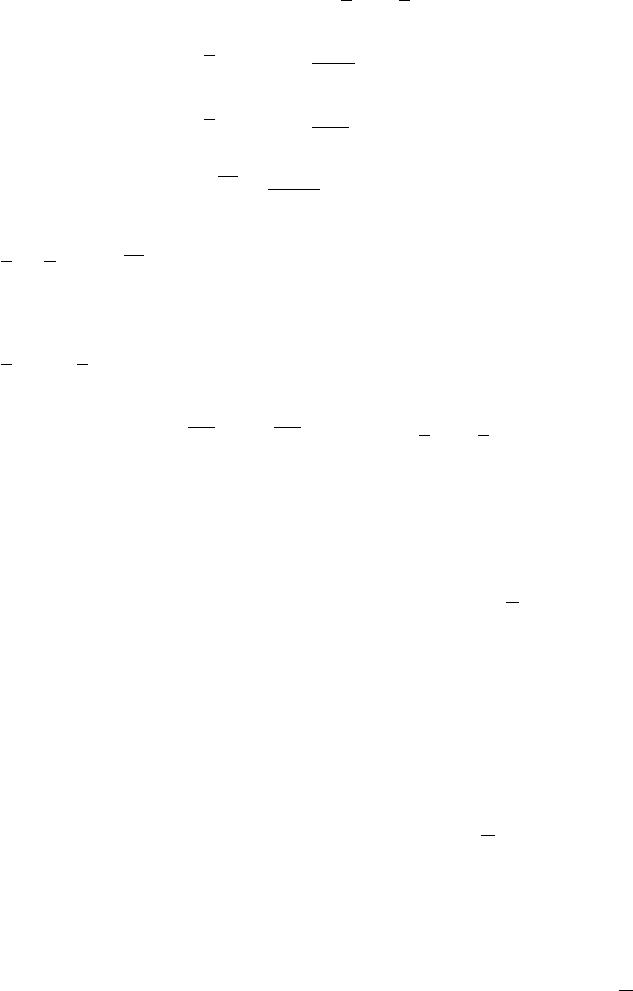
2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 47
Useful expressions following from these definitions include
u
k
c
=
˜
c(1 −
˜
c)(u
k,P
− u
k,R
) + O(γ),
u
k,R
= ˜u
k
−
u
k
c
1 −
˜
c
+ O(γ),
u
k,P
= ˜u
k
+
u
k
c
˜
c
+ O(γ),
u
k
=
τ
u
k
c
1 + τ
˜
c
+ O(γ). (2.13)
It can be seen that, if ˜u
k
and
u
k
c
are determined from transport equations, values of
u
k,R
, u
k,P
, and u
k
readily follow. The important implications of the first of Eqs. (2.13)
for gradient or counter-gradient scalar transport will be discussed later. Here we
simply note that
u
k
c
arises because of intermittency between reactants and products;
its sign is determined by the relative magnitudes of the conditional mean velocities
u
k,P
and u
k,R
.
A component of Favre mean square velocity is
u
2
k
= (1 −
˜
c)(u
2
k
)
R
+
˜
c(u
2
k
)
P
+
˜
c(1 −
˜
c)(u
k,P
− u
k,R
)
2
+ O(γ). (2.14)
The first and second terms on the right-hand side of Eq. (2.14) r epresent contributions
from turbulence in reactants and products, respectively, and the third term, which
appears as a flame-generated contribution to the turbulence intensity, is in fact again
a consequence of the intermittency between the mean velocities in reactants and
products. Its properties do not resemble those of a quasi-random turbulent field.
An alternative to this BML partitioning of the JPDF
P(c, u
k
; x) into contribu-
tions from reactants, products, and burning zones is to formulate conditional mean
transport equations for reactants and products [22–24]. These equations contain
additional terms, representing fluxes at the interface with the thin reaction zone,
which must be modelled. An advantage of such a formulation is that the flow in
reactants and products may be treated as having constant density. A possible dis-
advantage is that the interface flux terms depend on the reaction-zone structure at
a chosen isosurface location, and satisfactory general closure models have not yet
been demonstrated.
It is worth noting here that any multivariate PDF
P(c,ϕ
1
,ϕ
2
... ; x) involving
c(x, t) along with other variables ϕ
1
(x, t),ϕ
2
(x, t),..., can be partitioned in a manner
similar to that shown in Eq. (2.10), allowing conditional mean quantities in reac-
tants, products, and reaction zones to be defined and their relationships explored.
For example, premixed turbulent combustion with variable enthalpy is analysed in a
partitioned bivariate PDF of specific enthalpy and progress variable, [25] and in tran-
sient combustion in a spark-ignition engine in which the bivariate PDF is
P(c, T ; x, t)
[11]. A similar analysis is applied [26] to situations in which several chemical reac-
tions occur sequentially. Finally, BML fluid mechanics is recovered in an analysis
[27] incorporating systematically reduced reaction-rate mechanisms.
The application of the partitioning introduced in Eq. (2.6) can be further illus-
trated by considering the pressure gradient co-variances appearing in the transport
equations for Reynolds stress and flux components. Taking the term in the scalar
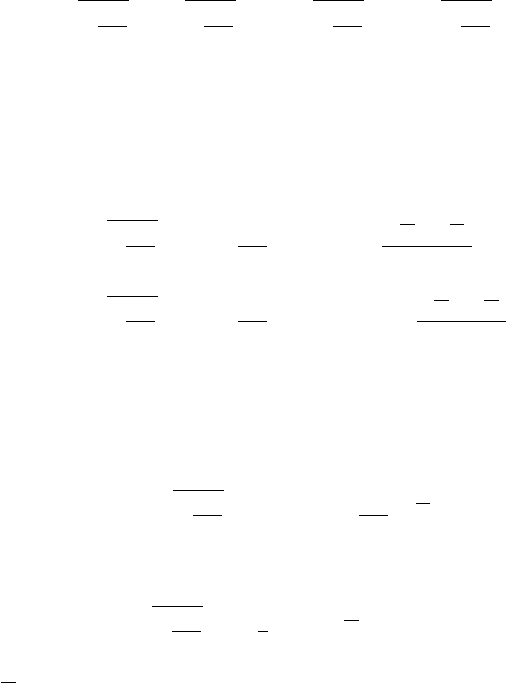
48 Modelling Methods
flux equation as an example, we have
c
∂p
∂x
k
= α
c
∂p
∂x
k
R
+ β
c
∂p
∂x
k
P
+ γ
c
∂p
∂x
k
F
. (2.15)
Note that, although γ 1, gradients through reaction zones may be larger than
those that are due to turbulence if
ˆ
N = τS
0
L
/u
rms
> Da
−1/2
[2], so the final term in
Eq. (2.15) must be retained. Domingo and Bray [18] developed a model for these
co-variances assuming that the reaction zones could be approximated by unstretched
laminar flames. The reactants and products contributions are
c
∂p
∂x
k
R
=
c
∂p
∂x
k
|c = 0
=−
˜
c
∂(
p
R
− p)
∂x
k
,
c
∂p
∂x
k
P
=
c
∂p
∂x
k
|c = 1
= (1 −
˜
c)
∂(
p
P
− p)
∂x
k
, (2.16)
and the conditional mean pressure gradients ∂p
R
/∂x
k
and ∂p
P
/∂x
k
are evaluated
from Euler equations applied upstream and downstream of the thin flame, respec-
tively, but neglecting additional terms representing fluxes at the interface with the
reaction zone [24]. The flamelet contribution,
γ
c
∂p
∂x
k
F
=
1−c
∗
c
∗
c
∂p
∂x
k
|c
P dc, (2.17)
with c
∗
→ 0, is evaluated by means of laminar flamelet assumptions, leading to
γ
c
∂p
∂x
k
F
=
1
2
τn · N
k
ρ
u
S
2
L
(0.7 −
˜
c), (2.18)
where
is the flame surface density, n and N
k
are unit vectors normal to the flamelet,
pointing towards reactant and in the direction of x
k
, respectively, and n ·N
k
is
treated as a constant of the order of unity. Models of these pressure gradient co-
variances with a wider range of applicability may be found in [12, 17, 28].
2.1.2 Application to Stagnating Flows
Predictions from the BML model were systematically tested and compared with
experimental data in a series of papers [29–32] addressing the problem of a pla-
nar turbulent flame brush stabilised in the vicinity of a stagnation point, which is
established either between two opposed turbulent jets, as illustrated in Fig. 2.3(a),
or on the surface of a plate arranged perpendicular to a single turbulent jet, as in
Fig. 2.3(b). These are convenient configurations for experiments and a large amount
of data were published [33–40].
Although the experiments of Kalt et al. [38] include the highest available tur-
bulence levels, much of the available experimental data involve turbulence of low
intensity, as measured by a parameter δ = k
1
/w
2
1
, where k
1
and w
1
represent the
turbulence kinetic energy and mean axial flow velocity, respectively, at the nozzle
exit.
2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 49
REACTANTS
z, w
r, u
r, u
z, w
w
1
z = d
BURNER
NOZZLE
PRODUCTS
FIELD OF VIEW
FOR FIGURE 3
REACTION
ZONE
(a) (b)
Figure 2.3. Sketches of stagnation point flow geometries: (a) stagnation plate (b) counterflow.
Figure 2.3 shows flow arrangements for stagnation point flow. The nozzle is
placed at a distance d from the stagnation plane, the axial coordinate is z, measured
from the stagnation point, and the radial coordinate is r. A dimensionless quantity
˜z = z/d is introduced for the analysis. With δ 1, this flow is dominated by pressure
gradients, and turbulent transport terms in the RANS equations are shown [29]to
be negligible. In the first stage of the analysis [29], the flame brush is shown to be
planar in the vicinity of the axis of symmetry. The relative unimportance of Reynolds
stresses and fluxes when δ 1istestedbyfirstimposing a mean progress-variable
distribution
˜
c(˜z) from experiment and calculating
ρ(˜z)fromEq.(2.1) and then solving
the mean-flow equations with these stresses and fluxes set to zero and showing that
predictions agree well with published experimental data. A second stage [30] begins
with
˜
c(˜z),
ρ(˜z), ˜w(˜z), and U(˜z) = ˜ud/w
1
r, all known from these calculations [29].
With these quantities provided, the uncoupled second-moment transport equations
are closed and solved to predict the Reynolds stresses
u
2
and
w
2
and the Reynolds
flux
w
c
. It is found that, in these circumstances, the pressure gradient co-variance
expressions described earlier [see Eqs. (2.17) and (2.18)] play an essential role in
these equations and give good agreement with available experimental data.
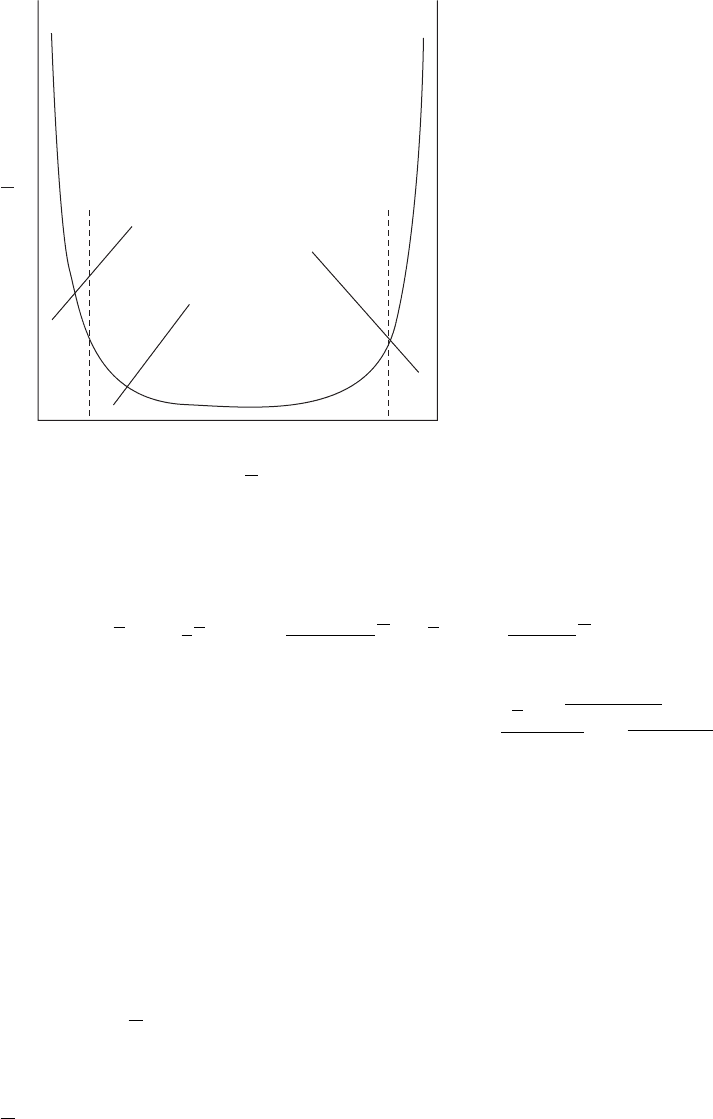
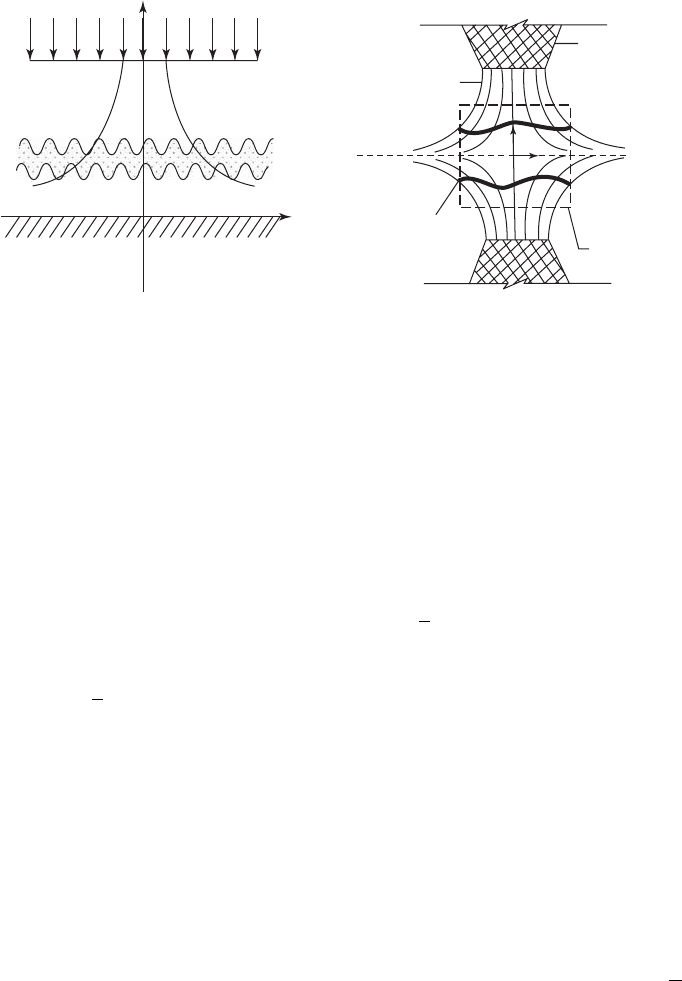
The turbulence intensity components, Fig. 2.4, are shown to be anisotropic and
strongly peaked inside the flame brush as a result of flame-generated ‘turbulence’
that is due to intermittency.
A further stage in the analysis of flames in stagnating flows [31] uses the mea-
sured mean progress-variable distributions
˜
c(˜z) from five different experiments to
calculate the corresponding experimental mean-reaction-rate distributions,
˙ω
c
(˜z).
It then makes use of earlier calculations [29, 30] to compare predictions from five
different mean-reaction-rate models with the experimental data. Only qualitative
agreement is found. Finally [32] the coupled model flow equations are solved di-
rectly, using a new laminar flamelet mean-reaction-rate model [41] [described in
Subsection 2.1.5; see Eq. (2.36)] and without any assumed mean progress-variable
distribution, and predictions are again found to be in satisfactory agreement with
published experimental data. It is also shown that an approximately sixfold increase
50 Modelling Methods
8
6
4
2
0
5
4
3
2
1
0
0 0.25
G
uu
G
ww
0.50 0.75
(a) (b)
1 0 0.25 0.50
z
0.75 1
z
~
~
Figure 2.4. Turbulence intensity components from the model of Bray et al. [30] (lines), com-
pared with experimental data of Li et al. [34] (data points): (a) radial intensity G
uu
=
u
2
/k
0
,
(b) axial intensity G
ww
=
w
2
/k
0
,wherek
0
is the turbulence kinetic energy at the nozzle exit.
From Bray et al. [30].
in a mean-strain-rate function is required for displacing the flame brush from a loca-
tion where flashback to the nozzle is about to occur to a position so close to the wall
that extinction is imminent.
2.1.3 Gradient and Counter-Gradient Scalar Transport
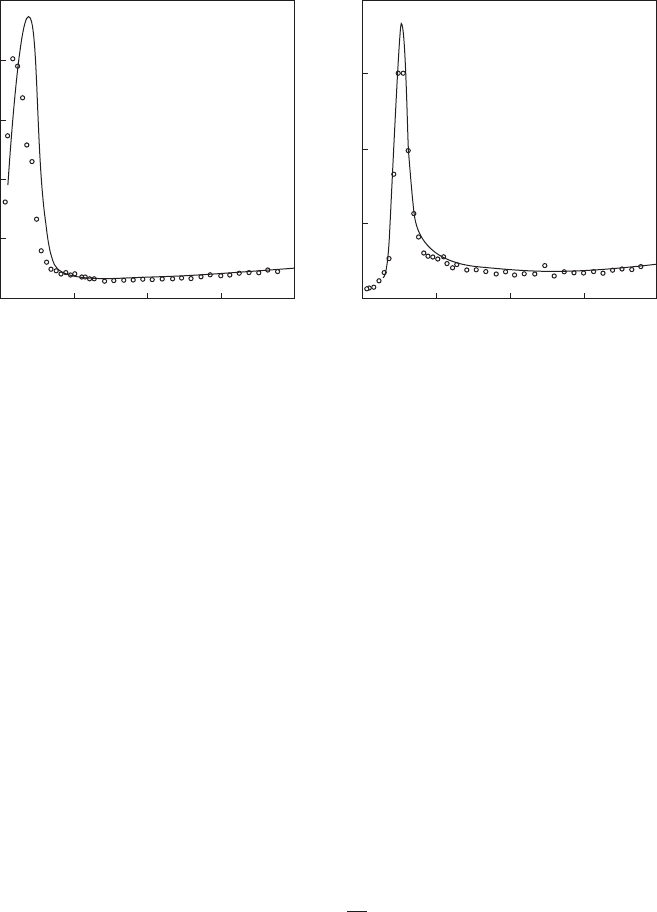
An important result of this asymptotic analysis of flames near stagnation points [30]
is that, to the lowest order in δ, the scalar flux transport equation reduces to an
algebraic expression:
w
c
=−τS
L
n · N
z
˜
c(1 −
˜
c). (2.19)
Counter-gradient scalar transport [6] therefore occurs because n · N
z
is positive
here, so
w
c
has the same sign as d
˜
c/dz, both being negative in the coordinate
system shown in Fig. 2.3. The scalar flux is in the opposite direction to that predicted
by the usual gradient transport expression of non-reactive turbulent flows, namely
w
c
=−ν
T
d
˜
c
dz
(2.20)
where ν
T
is a turbulent diffusivity.
As may be seen from Fig. 2.5,Eq.(2.19) gives excellent agreement with available
experimental data. Other experiments [42] and DNS calculations [1, 20, 43] confirm
the occurrence of counter-gradient transport.
Counter-gradient transport in premixed flames was first observed in experi-
ments by Moss [44] and was predicted in RANS calculations by Libby and Bray [6].
It was also predicted in calculations from other second-moment turbulent combus-
tion models [17, 45], and Zimont and Biagioli [46] proposed a model in which scalar
transport is described by the sum of a k– gradient transport expression and ‘gas
dynamic’ counter-gradient quantity. A theoretical and DNS analysis of planar turbu-
lent flames by Veynante et al. [1] identifies the increased conditional mean velocity

2.1 Laminar Flamelets and the Bray, Moss, and Libby Model 51
0
–0.5
–1
–1.5
0 0.25
G
wc
0.50
z
0.75 1
~
Figure 2.5. Axial scalar flux G
wc
=
w
c
/k
1/2
0
from the model of Bray et al. [30] (lines),
compared with experimental data of Li et al. [34] (data points). From Bray et al. [30].
in burned gases, resulting from the reduction in density, relative to the reactants, as
a cause of counter-gradient transport. The analysis therefore introduces the velocity
jump τS
0
L
across a laminar flame as the driver of counter-gradient transport, opposed
by a turbulence quantity α u
rms
, where u
rms
is the turbulence rms velocity ahead of
the flame. The quantity α is an ‘efficiency factor’ [47] measuring the influence of
eddies of different scales on a laminar flame. The scalar flux in an assumed planar
turbulent flame brush is then modelled as
u
c
=
˜
c(1 −
˜
c)(τS
0
L
− 2α u
rms
). (2.21)
This expression predicts that a transition from gradient to counter-gradient transport
occurs when
ˆ
N
∗
≡
τS
0
L
2α u
rms
≥ 1. (2.22)
Typical values of α are close to 0.5, so
ˆ
N
∗
is similar in magnitude to the parameter
ˆ
N = τS
0
L
/u
rms
introduced earlier. This criterion is supported by DNS data from [1]
and elsewhere. It is also in reasonable agreement with the experimental data of Kalt
et al. [38] in stagnation point flames in intense turbulence, although these authors
also suggest a modified expression.
In contrast to the expression of Veynante et al. in [1], Eq. (2.22), which depends
on the velocity jump τS
L
across a flamelet, the alternative criterion proposed by
Swaminathan et al. [48, 49] involves the internal structure of the thin reaction zone.

52 Modelling Methods
Considering a steady, planar, turbulent flame brush, they integrate the transport
equation for the variance of c [the first of Eqs. (2.3)] through the brush and show
thatthesignof
u
c
depends on the sign of
I =
∞
−∞
c
∂u
k
∂x
k
dx. (2.23)
If the peak in the conditional mean dilatation
∂u
k
/∂x
k
|c
occurs at a large value
of c, I > 0 and counter-gradient transport is favoured, but gradient transport is
indicated in situations in which the peak dilatation comes at smaller values of c.
They conclude that, unlike methane–air flames, counter-gradient transport will not
occur in stationary planar hydrogen–air flames with equivalence ratios greater than
about 0.5. However, in a more recent work, Chen et al. [50] s how that mean flow
divergence can modify this picture in such a way that either gradient or counter-
gradient transport can occur when I > 0.
Chakraborty and Cant [12] use DNS of planar turbulent flame brushes to explore
the influence of Lewis number Le =
ˆ
λ/c
p
ρD on scalar turbulent transport. The small-
Lewis-number flames are found to be much more strongly wrinkled and propagate
more quickly. They show that, under the same initial conditions of turbulence, flames
with Le < 1 exhibit counter-gradient transport, whereas flames with Le > 1 tend to
have gradient transport. The efficiency factor α in Eq. (2.22) is evaluated and found
to increase as Le decreases, and they conclude that the criterion of Veynante et al.
cannot correlate their data. Chakraborty and Cant [12] then test a wide range of
models to close the scalar flux transport equation and develop new closures including
Lewis number effects.
It is important to note that most of the experimental and DNS data that were used
to investigate scalar transport and to assess the criterion of Veynante et al. [1] involve
planar turbulent flame brushes in which Reynolds shear stresses are absent. A model
calculation by Masuya and Libby [51], representing a V-flame highly constrained
within a duct, indicates the presence of a mean scalar flux along the flame brush,
a direction in which the mean progress-variable gradient is zero. The existence
of this non-gradient transport is not predicted by inequality in Eq. (2.22). Also,
experimental data [42, 52] and DNS calculations [20] in more complex flow fields
sometimes show that the various components of the scalar flux at a given location
involve a combination of gradient and counter-gradient transport. The transition
between these two types of transport process in complex flows deserves further
study.
Most LESs of premixed turbulent combustion assume a gradient expression for
subgrid scalar transport. However, Tullis and Cant [53], using filtered DNS data,
show that regions of both gradient and counter-gradient transport can frequently
occur within the same simulation; LES closures were proposed [53] to address this
issue.
2.1.4 Laminar Flamelets
Damk
¨
ohler [54] proposed that a premixed flame in turbulence of sufficiently low in-
tensity and large scales can be viewed as a wrinkled laminar flame of increased
surface area per unit streamtube area, leading to a turbulent burning velocity
