Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames
Подождите немного. Документ загружается.


1.5 Equations of Turbulent Flow 13
contained in these larger eddying motions, it is difficult to find universal model ex-
pressions to close the system of equations. The large-eddy simulation technique was
developed to overcome this difficulty. In LES, the large-scale motions are resolved
in both space and time, but the small scales are not resolved, so the requirement for
spatial resolution is related to the larger eddying motions. Small scales are filtered
out by use of a localised spatial averaging (weighted by F ) of the form
ϕ(x, t) =
ϕ(x
, t)F [(x − x
); ]dx
, (1.19)
where F is a filter function whose shape is chosen so that it approaches zero when
x − x
exceeds the chosen filter size and also
F (x
)dx
= 1. The commonly used
shapes for F and their characteristics can be found in [4, 9]. A couple of points
worth noting at this stage are, that (1) the filtering operation does not commute with
derivative operators, and (2)
ϕ = ϕ and ϕ
= 0, unlike in RANS averaging.
The preceding averaging or filtering process results in loss of information about
small-scale motions, and consequently the filtered equations are unclosed because
they contain co-variance terms analogous to the Reynolds stresses in RANS. The
subgrid scale (SGS) model expressions with which the system of equations is closed
are often developed from the corresponding RANS models. A discussion of such
modelling for non-reacting flows can be found in [4]. For flows with density variation,
such as combustion, it is convenient to solve the Favre mean version of the LES-
filtered transport equations, which can be obtained by density-weighted filtering
given by
ρϕ(x, t) =
ρϕ(x
, t)F [(x − x
); ]dx
. (1.20)
Equations (1.19) and (1.20) suggest that the LES solution is expected to have
some dependence on the artificial (scale) parameter . This raises some fundamental
conceptual questions, as discussed by Pope [39]. Although it is not unexpected that
this filter scale will influence the degree of resolution in the LES solution, the
averaged solution obtained from the LES should be independent of the choice
of .
1.5 Equations of Turbulent Flow
The mass-weighted, Favre mean transport equations of turbulent reacting flow are
obtained by the averaging of the equations of Section 1.3. Equations (1.1)give
∂
ρ
∂t
+
∂
ρu
k
∂x
k
= 0,
∂
ρu
∂t
+
∂
ρu
k
u
∂x
k
=−
∂
ρ
u
u
k
∂x
k
−
∂
p
∂x
+
∂
τ
k
∂x
k
+ρ
N
i=1
Y
i
f
i
,
∂
ρ
Y
i
∂t
+
∂
ρu
k
Y
i
∂x
k
=−
∂
ρ
u
k
Y
i
∂x
k
−
∂
J
ik
∂x
k
+ ˙ω
i
. (1.21)

14 Fundamentals and Challenges
Similarly the simplified energy conservation expression of Eq. (1.10) becomes
∂
ρ
h
∂t
+
∂
ρu
k
h
∂x
k
=−
∂
ρ
u
k
h
∂x
k
−
∂
∂x
k
ρD
∂h
∂x
k
, (1.22)
and the equation for the mean mixture fraction is
∂
ρ
Z
∂t
+
∂
ρu
k
Z
∂x
k
=−
∂
ρ
u
k
Z
∂x
k
−
∂
∂x
k
ρD
∂Z
∂x
k
, (1.23)
from Eq. (1.17). These equations are applicable to both RANS and LES, where
ϕ
ψ
≡
ϕψ − ˜ϕ
˜
ψ. The important assumptions introduced in the derivation of
Eqs. (1.10) and (1.17) should not be forgotten.
Several types of additional information are required before these equations can
be solved: (1) The equations of state, Eqs. (1.4) and (1.5), must be averaged to provide
relationships among
p, ρ,
h, and
Y
i
. (2) Models must be provided for the Reynolds
stress components
u
u
k
and the corresponding scalar flux components
u
k
Y
i
,
u
k
h
,
and
u
k
Z
. (3) The highly nonlinear reaction-rate expression of Eqs. (1.12) and (1.13)
must be averaged; the nature of the closure model for t hese mean reaction rates will
depend on assumptions about the unresolved small-scale structure of the flame. (4)
In many cases the Reynolds number is sufficiently large for all the mean molecular-
transport terms in these first-moment transport equations to be ignored; otherwise
simplifying assumptions are required. (5) Last, it may be noted that, if the final
term in the second of Eqs. (1.21) represents buoyancy that is due to gravity, then
f
i
= g
and no additional modelling assumption is needed. The strategies required
to provide the additional information are discussed in Section 1.7.
1.6 Combustion Regimes
The quantities to be modelled to obtain a closed set of averaged equations involve
statistical relationships between the fluctuating variables, and these relationships
depend on the small-scale structure lost because of averaging. Damk
¨
ohler [40] iden-
tified two limiting situations: If all length and time scales of the chemical reactions are
small in comparison with the smallest scales of the turbulent flow, then combustion
should be restricted to thin, laminar-like reaction zones. The turbulent flow stretches
and distorts these so-called laminar flamelet combustion zones and so increases the
mean rate of heat release. At the other extreme, if the chemical length and time
scales are all large in comparison with the biggest scales of turbulence, the structure
of the reaction zone would be expected to be more random.
To test and utilise this insight, one must first introduce characteristic scales of
the turbulent flow and chemical reactions. Those of the turbulence can be expressed
in terms of the mean turbulence kinetic energy
k = u
u
/2 and its mean rate of
dissipation
ε = 0.5 ν
∂u
∂x
k
+
∂u
k
∂x
2
.
Then characteristic turbulence length and time scales are = (
k
3/2
/ε) and τ
T
=
(
k/ε), respectively. A typical rms turbulence velocity u
rms
= (2k/3)
1/2
is often used in
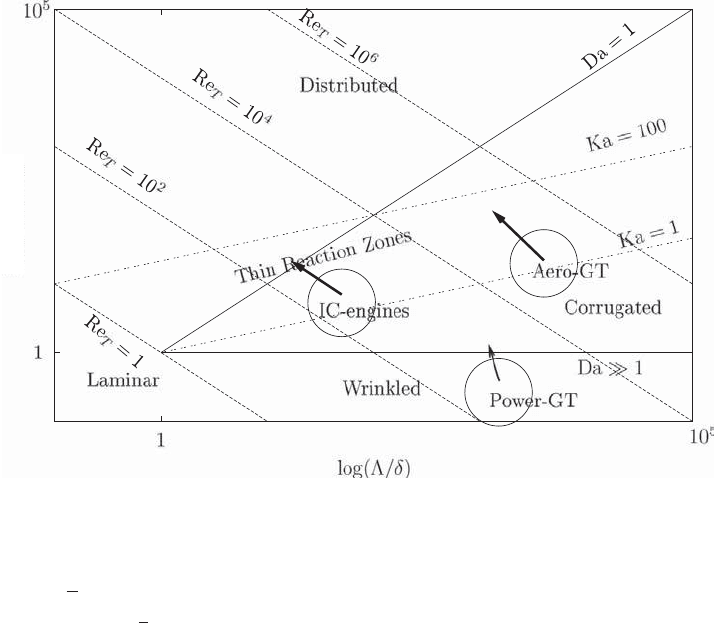
1.6 Combustion Regimes 15
S
L
0
log(u
rms
/ )
Figure 1.3. Turbulent combustion regime diagram. Typical combustion conditions in three
main categories of practical engines are shown, and the arrows indicate the likely direction of
change that is due to lean-burn technologies. GT, gas turbine.
place of k. The smallest length scale, limited by viscous dissipation, is the Kolmogorov
length η
K
= (ν
3
/ε)
1/4
, and the corresponding time scale is τ
K
= (ν/ε)
1/2
. It should be
noted that, in combustion systems, the predicted magnitudes of these characteristic
quantities can be significantly influenced by the choice of whether to evaluate the
kinematic viscosity ν(T ) in cold r eactants or hot products. It is convenient to use the
properties of an unstretched laminar flame to provide chemical scales. If the laminar
burning velocity of the premixed reactants is S
0
L
, then a characteristic diffusive
thickness is δ = D/S
0
L
, where D is a molecular-diffusion coefficient and τ
c
= δ/S
0
L
is the corresponding time. This diffusive thickness δ is often called the Zeldovich
thickness. One can also define a slope thickness, known as the thermal thickness δ
0
L
,
based on the maximum temperature gradient in and the temperature rise across an
unstrained laminar flame.
These characteristic scales may now be combined to form dimensionless pa-
rameters. The ratio of turbulence time to laminar flame time, Da ≡ τ
T
/τ
c
, is known
as a Damk
¨
ohler number. The quantity Re
T
≡ u
rms
/ν is a turbulence Reynolds
number. If the Schmidt number is 1 then Re
T
= u
rms
/(S
0
L
δ). A third important
parameter, known as the Karlovitz number, is the ratio of chemical to Kolmogorov
time scales, Ka ≡ τ
c
/τ
K
= δ
2
/η
2
K
. The relationship between these parameters can be
illustrated in the form of a regime diagram [7, 9, 41], in which either (Re
T
, Da) or
(/δ, u
rms
/S
0
L
) are used as coordinates. Such a diagram is shown in Fig. 1.3, depicting
various features. The line identifying Ka = 1 is called Klimov–Williams line.The
classical argument is that, when Ka < 1, laminar flame scales are smaller than all the
relevant scales of the turbulence; turbulent eddies can then only wrinkle a laminar
flame but cannot extinguish it. This is the laminar flamelets combustion regime, which
16 Fundamentals and Challenges
can be further classified into two regimes depending on the value of u
rms
/S
0
L
as in the
figure. If Ka > 1 but Da > 1, some scales of turbulence are smaller than those of the
laminar flame and the possibility of local extinction of a laminar flame is anticipated,
although τ
c
is still smaller than τ
T
.
DNS data analysis has been used to explore t he limits of flamelet combustion,
and it has been suggested that the Klimov–Williams boundary, above which turbu-
lence can influence the internal structure of a reaction zone, is shifted upwards above
the line Ka = 1. The details are in [9]. Finally, if Da < 1, all scales of turbulence are
smaller than those of a laminar flame and a more randomly distributed reaction
regime is anticipated. However, as discussed at greater length in Section 2.1, thin
flamelet-like reaction zones have been found to be more robust than is suggested
by this interpretation of the regimes diagram. A review by Driscoll [42] finds that
evidence of ‘non-flamelet’ behaviour is sparse.
The likely combustion regimes based on the data available in the literature for
three major categories of practical engines are shown in Fig. 1.3. These estimates are
made after the laminar flame scales are corrected for the temperature and pressure
of the reactants. Aeroengines do not currently operate in purely premixed modes
but, if one presumes a premixed mode, then the combustion conditions are likely
to occur at the border of the corrugated flamelets and thin-reaction-zones regimes.
The drive towards the lean-burn technologies that is due to emissions regulations is
likely to push these conditions towards lower values of global or overall Da, because
reaction rates are reduced in leaner mixtures. However, for gas turbines, it is quite
unlikely to involve local Da < 1, unless high-temperature air or product dilution
concepts are employed. These concepts and their possible modelling are discussed
in Section 5.1.
1.7 Modelling Strategies
Two main types of model are required for converting the first-moment equations of
Section 1.5 into a closed set: (1) a fluid mechanical model to describe the Reynolds
stress and Reynolds flux terms by means of equations involving only known mean
properties of the flow, and (2) a closure model for the mean values of highly nonlinear
chemical-reaction-rate terms. Although we describe these models separately, it must
be emphasised that, in reality, they interact strongly with each other. It is necessary
to account properly for, on the one hand, the influence of combustion and heat
release on the turbulent flow and, on the other, the effects of eddying turbulent
motion on the heat and mass transfer processes that accompany chemical reaction.
Combustion introduces very large variations in fluid density, and the corresponding
changes in the volume of fluid elements induce significant local velocity changes. Very
steep property gradients can result in regions of strong reaction, in which molecular-
transport processes play a vital role. Turbulent motion distorts and stretches these
thin regions and may further increase their gradients. A proper understanding of
these physical processes and their interaction is essential if realistic models are to be
developed. All models, together with their constituent submodels, must yield unique
solutions, and the variables that they predict must always lie within the physical
bounds of the quantities they represent. RANS models are considered first, and
then their adaption for LES is discussed.
1.7 Modelling Strategies 17
1.7.1 Turbulent Transport
In non-reactive turbulent flows, closure of the mean-flow equations is generally
obtained either through the so-called k–ε model, in which additional transport equa-
tions are closed and solved for the mean turbulence kinetic energy
k and its dissi-
pation rate
ε, or in a more detailed second-moment closure in which the transport
equation for
k is replaced with closed transport equations for all Reynolds stress and
flux components. In the presence of heat release it is convenient to replace
k and ε
with their Favre mean equivalents
k andε. Their modelled transport equations may
be written [10]as
ρ
∂
k
∂t
+
ρu
∂
k
∂x
=
∂
∂x
μ +
μ
T
σ
k
∂
k
∂x
−
ρε
−
ρu
u
m
∂u
m
∂x
− u
∂ p
∂x
+ p
∂u
∂x
P
,
ρ
∂ε
∂t
+
ρu
∂ε
∂x
=
∂
∂x
μ +
μ
T
σ
ε
∂ ˜ε
∂x
− c
ε2
ρ
ε
2
k
− c
ε1
ε
k
P. (1.24)
Additional terms are sometimes introduced to allow for other effects such as buoy-
ancy [43] or compressibility in high-speed flows [10]. The equation forε is essentially
ad hoc and contains empirical coefficients whose usual values are σ
ε
= 1.3, c
ε1
= 1.44,
and c
ε2
= 1.92. The terms marked as P need modelling.
An important feature of this modelling methodology is its incorporation of a
gradient transport assumption in which turbulent shear stresses are described, by
analogy with the molecular process, through an eddy viscosity
μ
T
= C
μ
ρ
k
2
ε
,
where the usual value of the coefficient is C
μ
= 0.09. The Reynolds stress components
are related to μ
T
by
ρu
u
m
=−μ
T
∂u
∂x
m
+
∂u
m
∂x
−
2
3
δ
m
∂u
k
∂x
k
+
2
3
ρ
kδ
m
. (1.25)
Using the decompositions ρ =
ρ + ρ
in ρu
= 0 gives u
=−ρ
u
/ρ. From the state
equation ρ T = const. and its averaged form
ρ
T = const., when combustion occurs
at constant pressure, one can show that
ρ
u
=−ρ
u
T
/
T . This r eadily gives a
model
u
=
u
T
T
. (1.26)
in terms of the scalar flux.
A s calar flux component may be determined from a gradient transport expres-
sion of the form
ρ
u
Y
i
=−
μ
T
σ
i
∂
Y
i
∂x
, (1.27)

18 Fundamentals and Challenges
where σ
i
is an empirically determined turbulent Schmidt number that is usually taken
to be about 0.7. However, it is found that the assumption of gradient scalar transport
can fail in premixed turbulent combustion, and this has led some researchers [44–
46] to develop more detailed second-moment models. Models of this kind can be
illustrated from the work of Bray, Moss, and Libby (BML) [ 47, 48], described in
Section 2.1.
It is convenient to introduce a reaction progress variable c(x, t), defined as a
reduced temperature or reaction product mass fraction, having values of zero in
reactants and unity in fully burned products. The transport equation for this instan-
taneous quantity is
∂ρ c
∂t
+
∂ρ u
k
c
∂x
k
=
∂
∂x
k
ρD
∂c
∂x
k
+ ˙ω
c
. (1.28)
By Favre averaging this equation, one obtains the following balance equation for
c:
∂
ρ
c
∂t
+
∂
ρu
k
c
∂x
k
=
∂
∂x
k
ρD
∂c
∂x
k
− ρ u
k
c
+
˙ω
c
, (1.29)
where the molecular transport is usually neglected compared with the turbulent
transport.
Its probability density function or PDF is denoted by
P(ζ; x), where ζ is a stochas-
tic variable corresponding to c(x, t). The PDF has the properties that its integral over
all possible states is unity and the integral of
P times a function of ζ gives the mean
value of the function so, for example, the Favre mean of c(x, t)is
˜
c(x) =
1
ρ
1
0
ρ(ζ) ζ P(ζ; x)dζ.
If the burning zone is made up of pockets of reactants, with probability α, and
pockets of products, with probability β, separated from each other by reaction zones,
having probability γ, then the PDF can be written as
P(ζ; x) = αδ(ζ) + βδ(1 − ζ) + γ f (ζ; x), (1.30)
with α + β + γ = 1. These weights depend on x and f (ζ; x)isthePDFoftheinternal
part of the distribution. If it is also the case that burning is restricted to thin reacting
zones or flamelets, whose characteristic dimension is small compared with all other
scales of the flow, then γ ∼ O(1/Da) 1 and the Favre mean of any property ϕ(c)
can be written as
ρϕ(x) = αρ
u
ϕ
u
+ (1 − α)ρ
p
ϕ
p
+ O(γ), (1.31)
where ρ
u
,ρ
p
,ϕ
u
, and ϕ
p
represent densities in reactants and products and values of
ϕ in reactants and products, respectively.
These thin-flamlets arguments can be extended to evaluate conditional mean
velocities in reactants and products, that is, mean values formed from velocity mea-
surements taken only when c = 0orc = 1, respectively, and written
u
k,u
=u
k
|c = 0
for reactants or
u
k,p
=u
k
|c = 1 for products, where the angle brackets indicate av-
eraging. It may then be shown (see Section 2.1) that
u
k
c
=
c(1 −
c)(u
k,p
− u
k,u
) + O(γ),
1.7 Modelling Strategies 19
so the direction of the scalar flux
u
k
c
is the same as that of the conditional mean ve-
locity difference
(
u
k,p
− u
k,u
)
. An explanation for counter-gradient scalar transport,
that is, transport in the direction opposite to that indicated by Eq. (1.27), is that force
fields that are due to pressure gradient [45] or Reynolds stress [49] act differentially
on low-density burned-gas pockets within the flame brush.
Second-moment models, in which transport equations are used to determine
second moments, variances, and co-variances, can be used to address these issues.
Reynolds stress components must satisfy [50–52]
∂
∂t
ρ
u
u
m
+
∂
∂x
k
ρu
k
u
u
m
=−
∂
∂x
k
ρ
u
k
u
u
m
+
u
g
m
+ u
m
g
− ρε
m
−
ρ
u
k
u
∂ ˜u
m
∂x
k
+ ρ
u
k
u
m
∂u
∂x
k
−
u
∂p
∂x
m
+ u
m
∂p
∂x
, (1.32)
and the scalar flux component
u
Y
i
obeys [10, 52, 53]
∂
∂t
ρ
u
Y
i
+
∂
∂x
k
ρ ˜u
k
u
Y
i
=−
∂
∂x
k
ρ
u
k
u
Y
i
+
Y
i
g
+ u
˙ω
i
− ρε
i
−
ρ
u
k
Y
i
∂ ˜u
∂x
k
+ ρ
u
k
u
∂
˜
Y
i
∂x
k
−
Y
i
∂p
∂x
. (1.33)
Closure models are required for all the terms on the right-hand sides of the preceding
two equations. The viscous term in Eq. (1.32) is given by
ρε
m
= u
∂τ
mk
∂x
k
+ u
m
∂τ
k
∂x
k
=
∂
τ
mk
u
∂x
k
+
∂
τ
k
u
m
∂x
k
−
τ
mk
∂u
∂x
k
+τ
k
∂u
m
∂x
k
.
The parts in the first set of square brackets are usually included with the third-order
correlation [54] because it represents diffusion, and those in the second set of square
brackets are known as viscous dissipation, which is obtained from the modelled
transport equation in Eq. (1.24) after the assumption of local isotropy [52, 54]is
introduced; ε
m
= 2δ
m
ε/3. Modelling of other terms in Eqs. (1.32), and (1.33)are
discussed by Jones [52], and an example of their application specifically to premixed
flames can be found in Section 2.4. The dissipation rateε is commonly modelled with
the second of Eq. (1.24). It is worth noting that the pressure-related terms in the
equations for
k,ε, and
u
u
m
can usually be neglected for open flames, but may not be
so for flames inside combustors. Possible modelling of the pressure–dilatation term
is discussed in Section 2.4.
20 Fundamentals and Challenges
The variance of Y
i
(x, t) is also needed, and it obeys
ρ
D
Y
i
2
Dt
= 2
Y
i
˙ω
i
− 2 ρ
i
− 2 ρ
u
k
Y
i
∂
Y
i
∂x
k
−
∂
ρu
k
Y
i
2
∂x
k
+2
∂
∂x
k
ρ ˆα
∂Y
i
2
∂x
k
+ 2
Y
i
∂
∂x
k
ρ ˆα
∂
Y
i
∂x
k
, (1.34)
in which closures are needed for third-moment, chemical reaction terms and the
mean scalar dissipation
ρ
i
= ρD(∂Y
i
/∂x
k
)
2
. The last two terms are small and are
usually neglected. The scalar dissipation rate has a dimension of (time)
−1
, and rep-
resents the reciprocal of a local time scale for molecular mixing. We will see later
that the scalar dissipation plays an essential role in most mean reaction rate models
for premixed combustion.
1.7.2 Reaction-Rate Closures
The PDF formalism also provides a means of evaluating the mean values of chemical
reaction rates. For example, if the chemical source term in the transport equation
for c(x, t)is ˙ω
c
(c)
1
, its Reynolds mean is
˙ω
c
=
1
0
˙ω
c
P dζ = γ
1
0
˙ω
c
f dζ, (1.35)
where the second expression follows from the PDF in Eq. (1.31) and the observation
that ˙ω
c
= 0 when c = 0orc = 1. By a similar argument, any property ϕ(c) that is
zero in both reactants and products, so ϕ(c = 0) = ϕ(c = 1) = 0, has a mean
ϕ =
1
0
ϕ P dζ = γ
1
0
ϕ f dζ.
Eliminating γ between these two equations, one sees that
˙ω
c
is proportional to ϕ.
The scalar dissipation ρ
c
= ρD(∂c/∂x
k
)
2
, whose mean appears as the dissipation
term in the transport equation for the variance
c
2
, is zero when c = 0 or 1 and is
therefore proportional to the mean reaction rate. A physical interpretation [55] (see
Section 2.1) is that, with γ 1, reaction zones resemble unstretched laminar flames,
for which both ˙ω
c
and
c
are unique functions of c. It can be shown [55] that
˙ω
c
=
2
ρ
c
(2C
m
− 1)
+ O(γ), (1.36)
where C
m
≡ c ˙ω
c
/ ˙ω
c
can usually be treated as a constant; typically it varies between
0.7 to 0.8 for lean hydrocarbon – and ultra-lean (φ ≤ 0.4) hydrogen–air flames. A
typical value of this parameter for hydrogen–air mixtures with 0.4 <φ≤ 1 is about
0.6 [56]. In situations in which γ 1, this equation allows the mean reaction rate to
be calculated in terms of the mean scalar dissipation, which is found from a closed
version of its transport equation. This approach is explored in Section 2.3.
1
For a single reaction with a heat release parameter of τ = (T
b
− T
u
)/T
u
and a Zeldovich number of
ˆ
β ≡ α T
a
/T
b
, the reaction rate is given by ˙ω
c
= B ρ (1 − c) exp
−
ˆ
β(1 − c)
1 − α(1 −c)
, where α = τ/(1 + τ)
and B = A
f
T
f
exp(−
ˆ
β/α) when the Lewis number is unity.

1.7 Modelling Strategies 21
The progress-variable approach previously outlined can be adapted to include
the effects of fluid dynamics on the reaction surface, as proposed by Bradley [57],
which is discussed in Section 2.3. The previous progress-variable approach can also
be adapted for partially premixed combustion [58] in which mass fractions depend
on mixture fraction Z as well as on c,soY
i
(x, t) = Y
i
[c(x, t), Z(x, t)]. The progress
variable can be defined in terms of fuel mass fraction Y
f
(x, t)as
c(x, t) =
Y
f ,r
[Z(x, t)] − Y
f
(x, t)
Y
f ,r
[Z(x, t)] − Y
f ,p
[Z(x, t)]
,
where the notation indicates that the fuel mass fraction in unburned reactants, Y
f ,r
,
depends on Z, which is a function of x and t. Similarly, Y
f ,p
, which is the mass
fraction of fuel in equilibrium products, is also a function of Z. These dependencies
introduce additional terms in the transport equation for c(x, t), Eq. (1.28), which can
be accommodated [58] by replacing the true reaction rate ˙ω
c
with an effective rate
˙ω
∗
c
= ˙ω
c
+ A(x, t) − B(x, t), (1.37)
where
A =
2(Y
f ,r
− dY
f ,p
/dZ)
Y
f ,r
− Y
f ,p
ρ N
zc
,
B =
1
Y
f ,r
− Y
f ,p
d
2
Y
f ,p
dZ
2
ρ N
z
.
These expressions introduce two additional scalar dissipation rates: N
Z
= D(∇Z ·
∇Z) is the dissipation of Z, and N
Zc
= D(∇Z ·∇c) is known as t he cross dissipation.
If Eq. (1.37) is averaged, then the dissipation rate
z
of the variance of Z and
zc
of
the co-variance
z
c
appear. It is clear that additional modelling is required.
Returning to fully premixed combustion, there are two ways in which PDFs
can be evaluated to determine mean reaction rates from Eq. (1.35). The first, more
empirical presumed PDF method assumes the PDF to be described by a specified
algebraic expression, containing parameters that are related to moments of the
argument(s) of the PDF. This approach becomes impracticable if the PDF depends
on more than one or at most two stochastic variables. An appropriate form for a
presumed PDF is provided by the beta function [10]; in the case of a monovariate
PDF
P(ζ; x), where the stochastic variable ζ, which is related to a flow variable ϕ(x, t),
lies between zero and unity, this leads to
P(ζ; x) =
ζ
(a−1)
(1 − ζ)
(b−1)
ˆ
β(a, b)
,
where a and b are functions of position x as they are related to the first and second
moments of ϕ by
a =
ϕ
2
(1 −ϕ)
ϕ
2
− ϕ, and b =
a(1 −
ϕ)
ϕ
.
22 Fundamentals and Challenges
The normalising factor
ˆ
β is the beta function [59], which is related to the gamma
function, and it is given by
ˆ
β(a, b) =
1
0
ζ
(a−1)
(1 − ζ)
(b−1)
dζ =
(a)(b)
(a + b)
;
the gamma function can be calculated with a fifth- or eighth-order polynomial ap-
proximation in [59]. This presumed form provides an appropriate range of shapes: If
a and b approach zero (in the limit of large variance), the PDF resembles a bimodal
shape of Eq. (1.30) whereas, if a and b are large (in the limit of small variance),
it develops a monomodal form with an internal peak. It has also been shown by
Girimaji [60] that this PDF behaves likes a Gaussian when
ϕ
2
is very small.
The alternative transported PDF method [61] provides a more rigorous means of
computing PDF shapes and evaluating the influence of finite-rate chemical reactions.
Take the PDF
P(ζ; x) as an example, where ζ is the stochastic variable corresponding
to ϕ(x, t). If we had a fully resolved time-dependent solution, then ϕ(x, t) would be
known, so ζ ≡ ϕ(x, t), and the instantaneous or ‘fine-grained’ probability would be
represented by the Dirac delta function δ(ϕ − ζ). It can then be seen that the PDF
is obtainable as the average of this delta function. Manipulation of the transport
equation for ϕ(x, t), together with the properties of the Dirac delta function, then
leads to the differential equation for
P (see [62] and Section 2.4). However, as
noted earlier, it is more convenient to work with mass-weighted, i.e., Favre mean,
quantities in flows with large variations in density, leading to the introduction of
a mass-weighted PDF
P(ζ; x) =
P(ζ; x)ρ/ρ, from which the Favre mean of ϕ(x, t)is
obtained as
ϕ(x, t) =
ϕ
max
ϕ
min
ζ(x, t)
P(ζ; x)dζ.
The mass-weighted PDF obeys the equation
ρ
D
P
Dt
=−
∂
∂x
k
u
k
|ϕ = ζ
ρ
P
−
∂
∂ζ
˙ω(ζ)
ρ
P
−
∂
2
∂ζ
2
D
∂ϕ
∂x
k
∂ϕ
∂x
k
ϕ = ζ
ρ
P
. (1.38)
The terms on the left arise from time variations and convection. In the first term
on the right, the notation u
k
|ϕ = ζ represents the mean of (u
k
−u
k
), subject to
the condition ϕ = ζ, and this term describes the influence of turbulent transport on
P. It is usually represented by assuming a gradient transport expression. However,
the transported PDF formulation can be extended [61] to encompass the joint PDF
(JPDF) of a scalar variable and the flow velocity, and the turbulent transport term
is then closed; an additional unclosed term then appears on the right-hand side of
the equation, involving fluctuations in pressure. With this addition, both gradient
and counter-gradient scalar transport can be predicted. Significantly, the second
term on the right in Eq. (1.38), representing effects of chemical reaction, is closed,
because ˙ω(ζ) is a function of independent variable ζ and
P is determined as part
of the solution. Also, as explained in Section 2.4, the transported PDF formulation
can again be extended to describe the joint PDF of several scalar variables – mass
fractions and temperature – so detailed and realistic chemical kinetic mechanisms
