Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

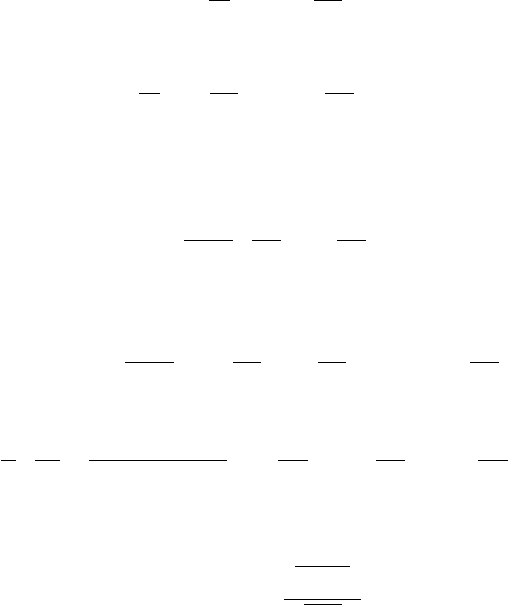
2.2 Flame Surface Density and the G Equation 63

thin-ﬂame reaction-zone regime. Hence the joint knowledge of the FSD and of the

laminar burning velocity S

is sufﬁcient to get a ﬁrst approximation of the heat

release rate in premixed turbulent combustion, further motivating the use of FSD.

Algebraic closures were proposed to express the FSD from resolved quantities [102 ]

or a balance equation for  may be solved.

FSD BALANCE EQUATION. The FSD balance equation may be derived from kinematic

considerations [94, 103], from surface analysis [82], or from scalar-gradient and PDF

equations [65]; in all cases, the scalar budget is written in its propagative form after

the introduction of the progression velocity of the isosurface relative to the ﬂow (or

displacement speed) S

(x, t) to express the absolute velocity of the isoscalar surface

Abs

= u

+ S

, (2.53)

with n

=−(∂ϕ/∂x

)/|∇ϕ|, the normal to the isoscalar surface, pointing towards

small scalar values. It is imperative that the displacement speed and the absolute

velocity be for isoscalar surfaces. By use of the absolute velocity and the mass

continuity equation, the scalar balance equation reads as

∂ϕ

∂t

+ ρu

Abs

∂ϕ

∂x

= 0, (2.54)

leading to

∂ϕ

∂t

+ u

∂ϕ

∂x

=−S

∂ϕ

∂x

= S

|∇ϕ|. (2.55)

This form of the scalar balance equation is further discussed in the subsection on the

G equation.

Equating Eqs. (2.49) and (2.55), we obtain

ρ|∇ϕ|



∂

∂x



ρD

∂ϕ

∂x



+ ˙ω



. (2.56)

The diffusive contribution may be decomposed exactly into a planar part to which a

curvature correction is added [55, 65, 83, 104]:

ρ|∇ϕ|





∂

∂x



ρD

∂ϕ

∂x





+ ˙ω



− D

∂n



∂x



. (2.57)

Now the corresponding FSD equation reads [56, 70]as





∂

∂t

∂



+ S





∂x





∂u

∂x

− n



∂u



∂x





∂n

∂x



. (2.58)

In this equation, the surface average in RANS (or ﬁltered surface average in

LES)





is deﬁned as







QG|ϕ

∗



G|ϕ

∗

. (2.59)

The right-hand side of Eq. (2.58) is the ﬂame stretch rate, composed of an in-

plane strain-rate term



∂u

/∂x

− n



(∂u



/∂x

)



and a curvature contribution



(∂n

/∂x

)



. Numerous closures exist in the literature to express the right-hand

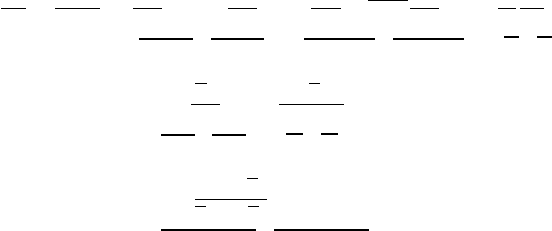
64 Modelling Methods

side of Eq. (2.58) (see [70] for a detailed review); it is usually decomposed into T

strain-rate term acting at the resolved scales of the simulation (for instance, induced

by the mean ﬂow ﬁeld in RANS or space-ﬁltered ﬁeld in LES), to which are added

, a strain-rate term that is due to the unresolved turbulent motions, and, P, a term

representative of ﬂame-area consumption by curvature or ﬂame interaction. Various

basic questions arise concerning the introduction of surface-based averaged (or ﬁl-

tered) quantities within usual ﬂow solvers, which are based on Eulerian single-point

quantities, a point that was further discussed in [105].

The most recent developments in FSD modelling applicable to premixed com-

bustion are within a LES context [80]. The balance equation for  then reads as

∂

∂t

∂u



∂x

∂

∂x





∂

∂x





 

(i)



∂

˜u

∂x

− n



∂

˜u



∂x







 

(ii)











 

(iii)

+ S



∂x







 

(iv)

−

∂S



∂x

  

(v)

+ β

∗

−ϕ

ϕ(1 − ϕ)

( − 

lam

)



 

(vi)

, (2.60)

where (i) is the turbulent transport of the FSD, i.e., transport by unresolved subgrid

scale (SGS) velocity ﬂuctuations, (ii) and (iii) are the resolved and SGS parts of

the strain rate, (iv) is the resolved curvature, (v) is the resolved propagation in the

direction normal to the ﬂame front, and (vi) is a dissipative term, combining SGS

contributions of propagation and curvature. u





is the SGS velocity ﬂuctuation taken

at a speciﬁc ﬁlter scale

 that is different from the LES ﬁlter size  used for the

momentum equations to account for the speciﬁc character of the response of the

ﬂame surface to the turbulent eddies cascade [106]. D



, σ

, , β

, and 

lam

are model

parameters, some of them are dynamically computed from the resolved ﬁelds; details

may be found in [80]. One of the major advantages of Eq. (2.60) lies in the fact that

it features a correct asymptotic behaviour if applied to laminar ﬂames; when the

turbulent velocity ﬂuctuations vanish, laminar ﬂame speed is properly reproduced

by Eq. (2.60), a point that may be of importance in LES to describe the stabilisation

of reaction zones through laminar ﬂame propagation.

2.2.2 The G Equation for Laminar and Corrugated Turbulent Flames

The FSD and G-equation approaches both describe premixed ﬂames as an interface

between a fresh mixture and burned gases. This geometrical description is closely

related to the ﬂamelet assumption in the sense that, once the interface is deﬁned

as a certain isosurface of temperature or species concentration in the ﬂame, all the

ﬂamelets may be parameterised by a distance to this interface. This concept can in

fact be generalised as long as the scale of the ﬂame is much smaller than the ﬂow

characteristic length scales, as for instance in large-scale ﬁre. This allows a proper

decoupling of the ﬂame–turbulence interactions from the chemistry.

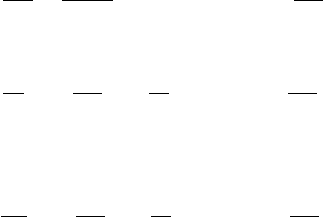
2.2 Flame Surface Density and the G Equation 65

For laminar and corrugated turbulent ﬂames with constant composition and

constant thermodynamic state of the fresh mixture, the ﬂame modelling is reduced

to the transport of the local FSD, or equivalently to tracking the interface position

and its evolution. In the context of the so-called G-equation model, the interface

is deﬁned as a surface G = G

of a level-set scalar G. This model was originally

introduced in [69] to illustrate the relationship between the wrinkling of a premixed

turbulent ﬂame and its turbulent ﬂame speed in the corrugated-ﬂamelets regime.

It must be kept in mind that the level set scalar G has a signiﬁcance only at the

G = G

surface. Elsewhere the level-set scalar may take any value. Nevertheless,

this implicit deﬁnition of the ﬂame-front position imposes a requirement to solve the

entire G ﬁeld to achieve the transport of the interface. For numerical reasons, the

G scalar is often chosen as the signed distance to the G = G

surface, which implies

that G

= 0. Additionally, the usual convention is to set G > 0 in the burned gases

and G < 0 in the fresh mixture. Then the transport equation for the level-set scalar

G is simply derived from the temperature or any reaction progress variable with

particular attention paid to the velocity of the G

surface.

As observed in relation (2.55), from a kinematic standpoint, the balance between

the diffusion and the reaction terms may be interpreted as an intrinsic displacement

speed of the interface, and relation (2.57) decomposes the diffusion contribution

into its normal and tangential parts. If the ﬂame is unstrained, the normal part of

ρS

, combined with the chemical source, is equal to the laminar burning velocity S

multiplied by the density of the fresh mixture ρ

. The second contribution on the

right-hand side of Eq. (2.57) may be positive or negative and represents the effect of

the curvature of the ﬂame front on the displacement speed. This contribution is noted

as ρ

κ,L

=−ρD

(∂n

/∂x

)orρ

κ,L

=−ρD

κ, where κ = ∂n

/∂x

is the curvature

of the ﬂame front. From this analysis the governing balance equation becomes

∂ρϕ

∂t

∂ρu

∂x

=−ρ

+ S

κ,L

∂ϕ

∂x

(2.61)

or, in non-conservative form,

∂ϕ

∂t

+ u

∂ϕ

∂x

=−

+ S

κ,L

∂ϕ

∂x

. (2.62)

The transport equation of the level-set G is then derived from progress-variable

Eq. (2.62) by means of a change of variables ∂G = ∂ϕ/|∇ϕ|:

∂G

∂t

+ u

∂G

∂x

=−

+ S

κ,L

∂G

∂x

. (2.63)

This transport equation for the level-set G clearly exhibits the different contri-

butions to the ﬂame-front velocity, namely the ﬂow velocity u, the laminar burning

velocity S

, and the curvature-induced velocity S

κ,L

. This transport equation is valid

for laminar ﬂames and turbulent ﬂames in the corrugated-ﬂamelets regime [55]. For

other regimes, or if the wrinkling of the ﬂame cannot be resolved, some additional

modelling is required.

In the wrinkled- and corrugated-ﬂamelets regimes, the smallest turbulent scales

are larger than the ﬂame thickness and the turbulent eddies may wrinkle only the

ﬂame front [55]. In the thin-reaction-zones regime, the smallest eddies may enter the

preheating zone and thicken the ﬂame brush, but these eddies do not interact with

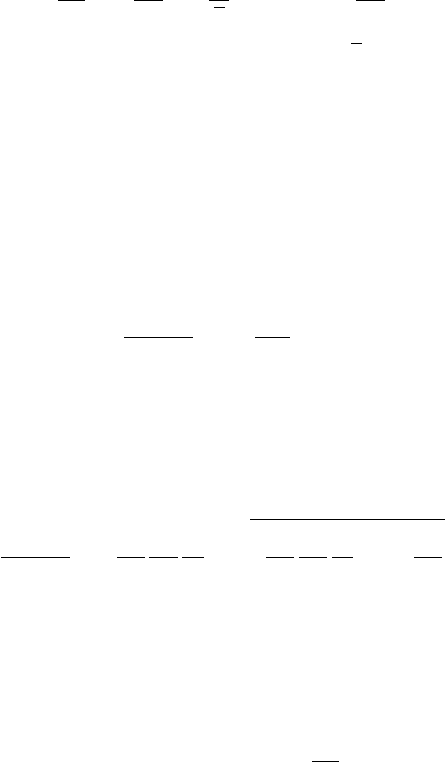
66 Modelling Methods

the reaction zone, which is an order of magnitude smaller than the ﬂame thickness.

In the previous regimes, the fresh mixture and the burned gases are still separated

by the inner layer, where the reactions occur. The ﬂamelet assumption is therefore

valid at the scale of the ﬂame thickness and may be used for further modelling. This

is not the case in the broken-reaction-zones regime, where the turbulent scales may

quench the ﬂame and lead to local extinctions. Then the ﬂamelet description is not

valid anymore because the gradients along the ﬂame front are large. Fortunately this

combustion regime is of limited interest for practical applications because the local

extinctions produce many pollutants such as unburned hydrocarbons and soot, and

they strongly affect the conversion rate of the burner.

In the other combustion regimes, a G-equation model may be derived from an

averaged progress variable in a RANS simulation or from a ﬁltered progress variable

in a LES following the procedure just detailed. In both cases, the G-equation model

for turbulent premixed combustion takes the form

∂

∂t

+ ˜u

∂

∂x

=−

+ S

κ,T

)ˇn

∂

∂x

, (2.64)

where ˜u denotes the Favre-averaged or ﬁltered velocity,

ρ is the Reynolds-averaged

or ﬁltered density, ˇn is the unit normal of the mean or ﬁltered ﬂame front pointing

towards the unburned gases, and S

and S

κ,T

are the intrinsic burning velocity of

the mean or ﬁltered ﬂame front and the increase or decrease of the burning velocity

that is due to resolved curvature, respectively. The mean or ﬁltered ﬂame front is

implicitly deﬁned as the

G =

isosurface. In this equation, the unclosed terms that

require a substantial modelling effort are the turbulent burning speeds S

and S

κ,T

The derivation of analytical closures for the turbulent burning speed S

has been

a very active ﬁeld since the pioneering work of Damk

ohler [54]. Detailed reviews

may be found in [55, 108]. One commonly used closure takes the following form:

− S

= C



rms



, (2.65)

where u

rms

is the turbulence rms velocity and C is a constant. The power m was

found experimentally to be close to 0.7. Nevertheless, this expression fails to agree

with experimental data in all of the combustion regimes. For this reason, similar

expressions were derived for both RANS simulation [55] and LES [109], respectively,

and take the form

− S

=−



(

)







+ b

, (2.66)

where the constants are b

= 1.0 and b

= 2.0. In a RANS simulation, D

is the

progress-variable turbulent diffusivity. In LES, D

is also the progress-variable tur-

bulent diffusivity used to represent unresolved SGS turbulent transport, but u



equal to the turbulent rms velocity at the ﬁlter scale u





. This expression satisﬁes two

important asymptotic behaviors: In the large-Damk

ohler-number limit, the turbu-

lent burning velocity S

scales linearly with the turbulence rms velocity u



, and in the

small-Damk

ohler-number limit, S

scales with u



√

Da. Other S

expressions have

been discussed in slightly different contexts, with algebraic closures [110]orfroman

2.2 Flame Surface Density and the G Equation 67

efﬁciency function used to ﬁne-tune ﬂame thickening in LES [106] or again from a

power-law ﬂame-wrinkling model [78, 79].

Concerning the resolved curvature contribution S

κ,T

, a closure similar to the

laminar case was proposed [55], simply accounting for the turbulent diffusivity:

κ,T

=−ρ

(

D +D

)

∂n

∂x

. (2.67)

This expression is also used in LES [109] if the Damk

ohler number Da



/(u





) is lower than unity, where l

is the reference laminar thermal ﬂame

thickness. It was then argued that the turbulent curvature contribution should van-

ish in the large-Damk

ohler-number limit and proposed for Da



> 1:

κ,T

=−ρ



D +D

−2





∂n

∂x

. (2.68)

Other expressions for the turbulent burning speed may be derived from higher-

order transport equations [55, 111] or from the FSD, for instance, alternative ap-

proaches for determining S

are also discussed in Subsection 2.3.6.TheG-equation

and FSD models share the same geometrical description of the turbulent ﬂame brush,

and many models may be transposable from one framework to the other.

In a RANS s imulation or a LES of turbulent premixed ﬂames, the G equation

provides only the position of the mean or ﬁltered ﬂame brush and its evolution.

Nevertheless, additional terms in the Navier–Stokes equations also have to be closed.

In the low-Mach-number limit, the density has to be prescribed everywhere in the

computational domain. Otherwise, in the generic framework of compressible ﬂows,

the heat release in the energy or enthalpy equation and the source term of any

progress variable or reactive species must be modelled. These necessary closures

have to be derived from the

G ﬁeld to ensure the consistency of the model.

Several approaches exist to evaluate the density or the source terms. The ﬁrst

one is a purely kinematic approach, in which the

G =

isosurface is considered to

be a sharp interface between the fresh mixture and the burned gases [75, 76, 112].

Consequently the density or any variable involved in the combustion process is

constant on each side of the level set and discontinuous at the interface

G =

Speciﬁc numerical methods may be used in this case to deal with the discontinuity,

like the ghost-ﬂuid method [113]. Alternatively, the temperature or density ﬁeld

may be ﬁltered on the computational mesh to avoid any numerical difﬁculty, as is

also done in the thickened-ﬂame model [106]. In the G-equation context, this latter

method usually requires many points in the ﬂame front. Because the thickness of

the ﬂame-brush is of primary importance to capture the ﬂame–turbulence interac-

tions in LES, a model was designed based on the ghost-ﬂuid method featuring an

arbitrary thickness of the ﬂame brush [114]. This thickness becomes an input to the

closure and may be obtained from analytical expressions [55]. Following the same

kinematic approach, the heat release and the progress-variable source term may be

evaluated from the volume swept by the level set because of the burning speed [115].

However, none of these methods gives a consistent modelling of the ﬂame-brush

thickness. Moreover, the coupling with a compressible solver for the computation of

combustion instabilities, for instance, is difﬁcult to perform.

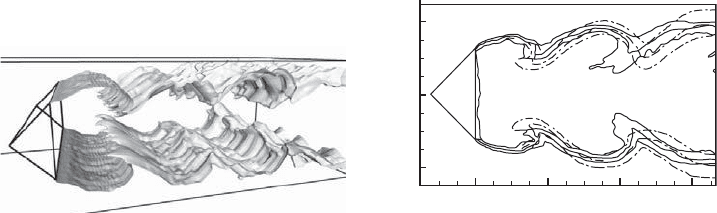
68 Modelling Methods

0.02

–0.02

Y (m)

X (m)

(b)

(

)

0.02 0.04 0.06

Figure 2.9. (a) LES: snapshot of the ﬂame surface; (b) comparison of experimental (solid

lines) [107] and LES (dot–dashed lines) progress-variable isocontours. The values of the

isocontours are 0.1, 0.5, and 0.9. The 0.1 isocontours are close to the channel walls and the 0.9

isocontours are close to the midplane, from [81].

These two last issues were recently addressed in a LES context [81]witha

coupled G-equation–progress-variable model. The G equation is transported to en-

sure the correct propagation speed of the ﬂame brush, and the progress variable

provides the species proﬁles in the ﬂame. The progress-variable source term is mod-

eled from the

G ﬁeld so that the progress-variable propagation speed is always

consistent with the

G ﬁeld. Figure 2.9 shows the application of the coupled G-

equation–progress-variable strategy to a turbulent premixed ﬂame anchored by a

triangular ﬂame holder. The stoichiometric premixed propane–air ﬂame under at-

mospheric pressure develops downstream of the triangular body [107], the ﬂame

surface interacts with the rolling up of the shear layers, and the progress-variable

isocontours are well reproduced by the simulation [Fig. 2.9(b)].

2.2.3 Detailed Chemistry Modelling with FSD

CHEMISTRY TABULATION. Detailed chemistry tabulation is widely used for the sim-

ulation of turbulent ﬂames; this tabulation may be completed before the burner

is simulated to drastically reduce CPU (i.e., CPU, central processing unit) time or

in situ during the simulation. In both cases, the detailed chemistry tabulation may

be conducted from the generic chemical point of view [116, 117], thus neglecting

molecular-diffusion effects or considering canonical ﬂame conﬁgurations to directly

include diffusion of species and heat, for instance, to mimic local ﬂamelet behaviour

[55, 99, 100, 118–123], a methodology that was in fact ﬁrst introduced for RANS

computations of diffusion [124] and premixed [98] ﬂames. These ﬂamelet methods

have been successfully used in RANS simulations and LESs of turbulent ﬂames with

steady premixed or non-premixed (diffusion) generated manifolds (i.e., composition

space trajectories tabulating chemistry from a few coordinates [63, 125–127]), along

with unsteady diffusion ﬂamelets [109, 128]. The LES of the forced ignition of an

annular bluff-body burner was conducted using such tabulated chemistry [129]; the

objective was to estimate the prediction capabilities of the LES in a fully transient

phenomenon. Figure 2.10 shows snapshots of 1 of the 20 ignition sequences that

were simulated by varying the spark position within the mixing zones, following a

preceding experimental study [130]. The LES observation agrees with experiment,

2.2 Flame Surface Density and the G Equation 69

Figure 2.10. LES-resolved instantaneous snapshots of temperature after sparking in a bluff-

body burner, from [129]. Solid black line: Isoline of stoichiometric mixture fraction. An image

covers a domain dimension of 70 × 70 mm; the temperature scale saturates at 1000 K to favour

low temperature levels. The ﬂow streamline is shown at sparking position in (a).

and comparisons with available measurements show that strain-rate effects need to

be included in the modelling of the ﬁltered burning rate; a correction to the usual

presumed PDF modelling associated with tabulated chemistry was then discussed

and validated to address this point [129], and this correction makes use of the FSD

concept suggesting that coupling PDF with FSD is an interesting option to improve

SGS modeling.

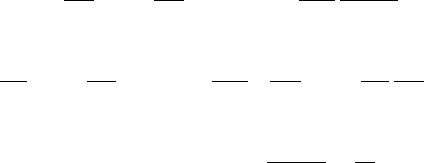
70 Modelling Methods

Flamelet-based chemistry tabulation may be summarized in a generic formalism

called multidimensional ﬂamelet-generated manifolds (MFMs) [101]. Considering

a detailed chemistry scheme of N species of mass fractions Y

(i = 1,...,N), a

restricted subset of dimension M < N composed of ϕ

subspace (or composition

space) variables is ﬁrst chosen, for instance from a direct analysis of the dynamical

response of the chemical system. The exact projection of the species and temperature

balance equations into this subset may be written [101]as

∂Y

∂τ



j=1

∂Y

∂ϕ

˙ω



j=1



k=1

ρχ

∂

∂ϕ

+ ˙ω

, (2.69)

∂T

∂τ



j=1

∂T

∂ϕ



˙ω

−



k=1

ρχ



∂c

∂ϕ



i=1

∂Y

∂ϕ





j=1



k=1

ρχ

∂

∂ϕ

−



i=1

˙ω

, (2.70)

where the usual notations are adopted and χ

= D∇ϕ

·∇ϕ

is the cross-scalar dissi-

pation rate between the scalars ϕ

and ϕ

. If one solves for the M balance equations

for ϕ

, which take the form of the usual species equations as in Eq. (2.49), together

with N + 1 − M equations in ϕ

space for Y

and temperature [Eqs. (2.69) and (2.70)],

the problem is still of size N +1 and therefore not yet reduced, but exactly projected

into a given ϕ

composition space. Two options allow f or reducing the problem size:

Equations (2.69) and (2.70) are solved prior to the simulation, with appropriate

boundary conditions, to construct a look-up table,

= Y

MFM

(ϕ

,...,ϕ

,τ; χ), (2.71)

T = T

MFM

(ϕ

,...,ϕ

,τ; χ), (2.72)

to store the thermochemical response as function of ϕ

so that only M equations

need to be solved with the ﬂow [101]. In Eqs. (2.71) and (2.72), χ denotes the

full set of scalar dissipation rates (SDRs). Figure 2.11 illustrates such detailed

chemistry tabulation, OH mass fraction trajectories versus a progress of reaction

are plotted for various equivalence ratios and strain-rate levels.

Equations (2.69) and (2.70) are solved during the simulation, according to local

ﬂow conditions, but for a reduced number of dimensions M. These equations

are usually easier to solve numerically than the primitive species equations

deﬁned in physical space, because the projection into the composition space ϕ

naturally acts as a zoom into the thin-ﬂame zone, hence reducing the resolution

requirement [55].

In both options for M = 1, if ϕ

is a reactive species (passive scalar) usual premixed

(diffusion) ﬂamelet modelling is recovered. The situation with M > 1 allows for

improving the description of chemistry in lean premixed combustion modelling or

for addressing hybrid combustion regimes, as in stratiﬁed or partially premixed

ﬂames [101]. The ﬁrst option is quite easy to couple with ﬂow solvers, but may lack

generic character because the boundary condition of the ﬂamelets are ﬁxed once

and for all, as for instance pure fuel and pure air. The second option is more CPU

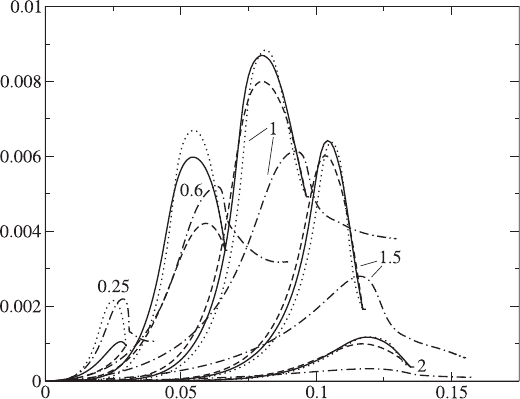
2.2 Flame Surface Density and the G Equation 71

Figure 2.11. Tabulated OH trajectories vs. progress of reaction using a 2D composition space

(M = 2, mixture fraction and reaction progress), from [101]. Equivalence ratios are given in

the graph, and various progresses of reaction scalar-dissipation-rate levels are considered,

Dotted, 1 s

−1

;solid,5s

−1

; dashed, 20 s

−1

; dot–dashed, 1D diffusion ﬂamelet response for

comparison (scalar dissipation rate of 40 s

−1

time consuming, but potentially more precise because the boundary conditions used

to solve (2.69) and (2.70) can be constructed from the local ﬂow conditions feeding

the reaction zones. In the ﬁrst option, the self-similar behaviour of ﬂames is of great

help to reduce the size of the chemical database [131].

With the rapidly growing computer capabilities, modern simulations of real burn-

ers involving many billions of computational cells will soon feature a mesh resolution

of about 100 μm, which is not sufﬁcient to resolve the intermediate radical-species

signals, but enough to fully capture the ϕ

signal based on major species (CO

,CO,

O), speciﬁcally in the lean premixed combustion regime. Therefore all ingredi-

ents of the tabulation (ϕ

, χ) will be fully resolved in these coming and advanced

simulations, and no submodel will be needed for simulating the control parame-

ters of the chemical table. In this future context, turbulent combustion modelling

will be reduced to the building of accurate chemistry reduction, for instance by

means of Eqs. (2.69) and (2.70). These highly reﬁned simulations may become the

standard tool for engineering design within the next decade, following the rapid

development of massively parallel computing, but meanwhile, there is still room

for the modelling of unresolved ﬂuctuations of ﬂame properties to conduct simula-

tions of many turbulent combustion applications. In this framework, both FSD and

the G equation are useful tools to couple with a given detailed chemistry look-up

table.

2.2.4 FSD as a PDF Ingredient

FSD provides information on ﬂame-front position and ﬂame wrinkling. This infor-

mation on ﬂame topology can be introduced in coarse-grid simulations to presume

72 Modelling Methods

the unresolved properties of progress variables of a detailed chemistry tabula-

tion [41, 132], usually approximated from presumed PDFs, which are built from

ﬁrst- and second-order moments of their variables. In lean premixed combustion

without any stratiﬁcation of equivalence ratio (i.e., no dilution with air or burnt

products having a different equivalence ratio) and without heat loss, chemistry tab-

ulation may be based on a single progress variable [99, 100]. The challenge is then

to estimate the unresolved statistical properties of this progress variable as its SGS

variance, ϕ

= ϕ

− ϕ

[132]. The production and dissipation of this SGS scalar en-

ergy are highly sensitive to ﬂame properties, and selecting closures that are derived

from chemically frozen ﬂow scalar-mixing studies may not be the best compromise

for capturing thin reaction zone behaviors. One option consists of relating the SGS

variance to the FSD, to estimate the variance from the FSD equation, so that the

topology of the ﬂame front enters the modelling. The shape of the PDF is then

presumed from the knowledge of

ϕ and , instead of ϕ and ϕ

DEFINITION OF -PDF. For a thin ﬂame, the premixed ﬂame -PDF may be cast

as [41, 132]

P(ϕ

∗

; x, t) = α(x, t)δ(ϕ

∗

) + β(x, t)δ(1 − ϕ

∗

) +

(x, t)

G(ϕ

∗

)

H(ϕ

∗

)H(1 − ϕ

∗

), (2.73)

where H denotes the Heaviside function. This PDF must satisfy



P(ϕ

∗

; x, t)dϕ

∗

= 1;



∗

P(ϕ

∗

; x, t)dϕ

∗

= ϕ;



∗

P(ϕ

∗

; x, t)dϕ

∗

= ϕ

. (2.74)

With Eq. (2.73), the constraint on the square of the progress variable reads [132]as

 =

, (2.75)

where ϕ

is the difference between the maximum variance level allowed and the

variance ϕ

[132],

= ϕ(1 − ϕ) − ϕ

= ϕ − ϕ

, (2.76)

and δ

is a characteristic ﬂame-length scale deﬁned as



1−



∗

(1 − ϕ

∗

)

G(ϕ

∗

)

dϕ

∗

. (2.77)

Assuming that combustion occurs in the thin-ﬂame-front regime, G(ϕ

∗

) may be

computed from the chemistry tabulation based on premixed ﬂamelets. The PDF

second-order moment is then deduced from the FSD with relation (2.75). The α and

β coefﬁcients of (2.73) are conveniently expressed from

ϕ and  [132]as

α = (1 −

ϕ) − 



1−



1 − ϕ

∗

G(ϕ

∗

)

dϕ

∗

, (2.78)

β =

ϕ − 



1−



∗

G(ϕ

∗

)

dϕ

∗

, (2.79)

respectively.