Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames
Подождите немного. Документ загружается.

2.3 Scalar-Dissipation-Rate Approach 83
where the term representing local flame propagation is
U
L
i
=
S
L
1 + u
rms
/S
L
∂
c
∂x
k
+
,
∂
c
∂x
∂
c
∂x
.
This proposal was revisited later in [166], and it was noted that the factors Re
1/2
T
are no longer present in the last two terms on the right-hand side that represent
turbulent stretching and dissipation–curvature effects.
DEPARTURE FROM THE FLAMELET REGIME – BRIDGING MODEL. One can also be inter-
ested in a closure that is valid for the situation of finite-rate chemistry. In the case
of highly turbulent flames (thickened-flame regime), the derivation of a transport
equation for the SDR of a reaction progress variable c was proposed first by Borghi
and Dutoya [164]. In this specific case of thickened turbulent flames, because diffu-
sion and chemical processes are not as strongly coupled as in the flamelet regime
of turbulent combustion [166], the reactive contribution (IX) of Eq. (2.97) can be
evaluated separately without considering the dissipation term (VIII). This means
that the previous modeled Eq. (2.96) can be used but with the additional reactive
term (IX) of Eq. (2.97), which must be closed:
∂
ρ
c
∂t
+
∂
∂x
k
(ρu
k
c
)
=
∂
∂x
ρ ˆα
T
∂
c
∂x
+ C
P
Y
ρ ˆα
T
ε
k
∂
c
∂x
k
∂
c
∂x
k
+C
P
U
ρν
T
c
k
∂u
∂x
k
∂u
∂x
k
+ ρ
c
A
e
ε
k
− β
c
c
2
+2D
∂c
∂x
k
∂ ˙ω
c
∂x
k
. (2.102)
In principle, a two-point statistical description is required for closing this reactive
contribution. As, in general, only single-point information is available, an addi-
tional hypothesis is required. Using, for instance, the linear mean-square estimation
(LMSE) formalism of Dopazo and O’Brien [181], one obtains the following closure:
2
ρ ˆα
∂c
∂x
k
∂ ˙ω
c
∂x
k
=
ρ
τ
c
c
∂ ˙ω
c
∂c
c
2
P(c)dY, (2.103)
where
P(c) is the one-point, one-time scalar Favre PDF of c.
Equation (2.102)for
c
is strictly valid for small values of the Damk
¨
ohler number
Da. For vanishingly small values of Da, the reactive contribution (IX) expressed by
Eq. (2.103) is negligible – the gradients of both the chemical rate and progress
variable become very small in the physical space – and it can be dropped from the
analysis and finally, because at large Re
T
, the instantaneous gradients of c are fixed
by turbulence rather than by chemical reaction; thus Eq. (2.94) can be used instead
of Eq. (2.102) to obtain
c
.
The previous result can be used to obtain a more general algebraic closure of the
SDR applicable to a wide range of conditions in terms of the Damk
¨
ohler number.
Indeed, in the case of premixed flames when combustion occurs in the flamelet
regime of turbulent premixed combustion, it is well known that there is a direct
proportionality between the mean chemical rate and the mean dissipation rate of
84 Modelling Methods
reactive scalar fluctuations. This result, which is strictly valid for infinite values of the
Damk
¨
ohler number, was recalled at the beginning of this section through Eq. (2.86).
By deriving a transport equation for c(1 − c) and considering that this is zero in
the limit of a very large Damkohler number, one obtains the following identity for
the instantaneous dissipation rate:
ρ N
c
= ρ ˆα
∂c
∂x
k
∂c
∂x
k
=
˙ω
c
2
(2c − 1). (2.104)
After averaging, the following result is obtained:
ρ
c
=−ρ ˆα
∂
c
∂x
k
∂
c
∂x
k
+
(2C
m
− 1)
2
˙ω
c
, (2.105)
which is nothing but the BML result in Eq. (2.86). In the other limit, that of a very
low Damk
¨
ohler number, turbulence dominates the chemical reaction to generate
scalar gradients, and this is expected to contribute in the non-reactive regions [160],
commonly known as the ‘out-of-flamelet’ contribution. This contribution is given by
Eq. (2.94). Hence the simplest strategy to recover these two limits is to use a linear
bridging function, depending on the value of the fluctuation-level parameter g by
ρ
c
= g
−ρ ˆα
∂
c
∂x
k
∂
c
∂x
k
+
(2C
m
− 1)
2
˙ω
c
+ (1 − g)C
D
ρ c
2
τ
T
. (2.106)
This closure was extended to partially premixed situations in [182 ] and success-
fully applied to stratified conditions in [141]. Such conditions are of special interest
for lean premixed flames that often propagate in imperfectly premixed mixtures of
fuel and oxidiser.
Having discussed the complexities associated with the chemical reaction, we
should now focus our attention on the effects induced by thermal expansion.
EFFECTS OF THERMAL EXPANSION. The heat release will duly influence turbulence,
which in turn will affect the reactions. Thus there is a close coupling among chemical
reactions, turbulence, and molecular diffusion in turbulent premixed flames [70, 183],
which needs to be captured for successful modelling. Swaminathan and Bray [150]
showed that the turbulent flame propagates significantly faster when the density
change across the flame front, represented by (X) in Eqs. (2.91), is considered in the
analysis. Bychkov [184] and Akkerman and Bychkov [185] made similar observations
about the influence of heat release on the flame propagation speed. DNS [177,
186–188] and experimental [189] studies showed that the dilatation changes the
characteristics of a turbulence–scalar interaction, resulting in the dissipation of the
scalar gradient, rather than its production, by turbulence. It will be shown later in this
section that these effects appear at leading order. Because of this, the scalings used
earlier in this section are likely to be modified and it is possible to use the laminar
flame speed S
0
L
or the turbulence rms velocity u
rms
to scale the fluctuating velocity.
However, if one uses the rms velocity then the dilatation-related term is found [190]
to be a lower-order term, which is contrary to intuition and observations in recent
studies. Thus the planar laminar flame speed is used in the following analyses.
For the situation with heat release from chemical reactions, one cannot neglect
any of the terms in Eq. (2.90); however the dilatation-related term (X) can be

2.3 Scalar-Dissipation-Rate Approach 85
simplified if one considers the combustion to be adiabatic with unity Lewis number in
low-Mach-number flows. These are reasonable approximations for typical practical
situations. Now, by use of the equation of state, the instantaneous and averaged
densities can be simply related to the progress variable and its Favre average by
ρ =
ρ
u
1 + τ c
,
ρ =
ρ
u
1 + τ
c
,
where τ is the heat release parameter (see Section 2.1). These relations allow one to
write [150]
(X) = 2
ρ
c
∂u
∂x
. (2.107)
This term involves the correlation between the SDR and dilatation, which turns out
to be a leading-order term, as one will see in the OMA presented next. It is to be
noted that this term was not hitherto considered in the analysis.
ORDER-OF-MAGNITUDE ANALYSIS. The turbulent integral length and time scales and
reactant density are used to scale the spatial derivative of mean quantities, time
derivative, and the density. The mean velocity is scaled with a reference velocity U
ref
and the diffusivity is scaled with S
0
L
δ
0
L
, as noted earlier. Because the gradient of the
progress variable is non-zero only inside the flame front, the quantities involving this
gradient are scaled with the laminar flame scales. Defining Re
T
≡ u
rms
/(S
0
L
δ
0
L
) and
Da ≡ S
0
L
/u
rms
δ
0
L
, and using the previous scalings, one obtains
(I) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Da
−1
,
(II) O
ρ
u
S
0
L
δ
0
L
2
c
2
;
Da u
rms
U
ref
−1
,
(III) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
−1
T
Da
−1
,
(IV) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Da
−1
,
(IV-b) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
−1
T
Da
−1
,
(V) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
−1/2
T
Da
−1/2
,
(VI) O
ρ
u
S
0
L
δ
0
L
2
c
2
;
Dau
U
ref
−1
,
(VII) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
0
T
Da
0
,

86 Modelling Methods
0.08
0.06
0.04
0.02
0
–0.02
–0.04
–0.06
–0.08
1
0.5
0
–0.5
–1
–1.5
0 0.2 0.4 0.6
c
0.8 1 0 0.2
(
a
)(
b
)
0.4 0.6 0.8 1
Ter ms
Ter ms
(V) + (VI) + (VII)
(IV) + (VI-b)
(VIII)
(VIII)
(III)
(X)
(IX)
(IX)
~
c
~
Figure 2.12. Variations of terms in Eq. (2.90) for (a) high-Da (Da = 6.84, Ka = 0.54, Re
T
=
56.7, τ = 2.3) and (b) low-Da (Da = 0.32, Ka = 13.2, Re
T
= 47, τ = 3.0) flames considered in
[191]. These DNS flames are statistically planar, have a Zeldovich number of 6.0, and a unity
Lewis number. The values given above are normalised by ρ
u
S
0
L
4
/ ˆα
2
.
(VIII) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
0
T
Da
0
,
(IX) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
0
T
Da
0
,
(X) O
ρ
u
S
0
L
δ
0
L
2
c
2
;Re
0
T
Da
0
. (2.108)
It is evident from the preceding equations that (VII), (VIII), (IX) and (X) are the
leading-order terms for high-Damk
¨
ohler-number flames and the other terms are
likely to be non-negligible when combustion occurs at low Da. This can be verified
by use of DNS or laser diagnostics data. However, spatial and temporal resolutions
required for resolving gradients of the progress-variable fluctuation and its reaction
rate preclude the use of laser diagnostics data at this time and the use of DNS data
is inevitable. Figure 2.12 shows the behaviour of various terms across a statistically
planar flame brush [191]. The values are appropriately normalised by use of the
reference density, planar laminar flame speed, and the reference diffusivity. The case
of a high-Da flame (Da ≈ 6.84) is shown in Fig. 2.12(a), and the low-Da (≈ 0.32) case
is shown in Fig. 2.12(b). A positive value in this figure implies a source, whereas a
negative value indicates a sink for the Favre-averaged SDR,
c
. The following points
are evident from this figure [191]:
r
the most dominant contributions come from the turbulence–scalar interaction,
dilatation, dissipation, and chemical reaction processes for both the flames.
r
The chemical reactions (IX) and dilatation (X) provide dominant sources
whereas the turbulence–scalar interaction and dissipation processes provide
dominant sinks. More detailed analyses [176, 186, 191, 192] clearly showed that
major contributions, by nearly an order of magnitude, of the turbulence–scalar

2.3 Scalar-Dissipation-Rate Approach 87
interaction effects come from (VII) for high-Da flames whereas it is quite likely
to have equal contributions from all of the three terms for low-Da situations.
r
The most apparent difference is on the physical behaviour of the turbulence–
scalar interaction process. It is clear from Fig. 2.12 that this process destroys
the (negative-value) scalar gradient in high-Da situations whereas it produces
the (positive-value) Scalar gradient in most parts of the flame brush in low-
Da situations. Small negative values can also be noted in Fig. 2.12(b) for
c ≥
0.65, implying that strong heat release in those regions is destroying the scalar
gradients. This is intuitively correct, as one would expect, but requires further
close understanding to help model construction.
These relative behaviours among the various terms and their components in the
SDR transport equation are also observed for non-unity Lewis number situations
[168, 193] and the dominant terms noted in Fig. 2.12 remain dominant. However, their
magnitudes increase as the Lewis number decreases [193] because thermodiffusive
(TD) instability, noted in Section 3.1, significantly increases the reaction rate when
the Lewis number is smaller than unity. The increased reaction rate results in an
increase of scalar and velocity gradients, yielding larger magnitude for all the terms
shown in Fig. 2.12. When Le > 1 the magnitudes of these terms are smaller than for
the Le = 1 case; their relative behaviours, however, remain the same [193]. It is clear
from the previous discussion that the dominant terms shown in Fig. 2.12 are likely to
remain dominant for a wide range of flow and thermochemical conditions, spanning
from the corrugated-flamelets to the thin-reaction-zones combustion regimes when
Da > 1. Hence one can envisage developing an algebraic model for the SDR by
balancing the dominant terms, which can be used in Eq. (2.86) to obtain the mean
reaction rate. However, one should be careful for low-Da cases, and it is quite likely
that the SDR transport equation, Eq. (2.90), will then need to be solved. Before an
attempt is made to derive an algebraic model for
c
, the closure models proposed
in the earlier discussion on the dissipation-rate transport equation are to be revised,
where necessary, to capture the close coupling among turbulence, heat release, scalar
mixing, diffusion, and molecular dissipation. Hence the modelling of unclosed terms
is considered next.
MODELLING OF TURBULENT TRANSPORT TERM (IV). Scalings in Eqs. (2.108)give
(IV)/(IV-b) ∼ O
(
Re
T
)
, which indicates that the modelling of the turbulent flux
of the SDR,
ρ u
k
c
, which is often modelled with the gradient hypothesis, is essen-
tial. This flux is counter-gradient when
ρ u
k
c
(∂
c
/∂x
k
) > 0, and it is gradient when
ρ u
k
c
(∂
c
/∂x
k
) < 0. A typical behaviour of this flux in statistically planar flames is
showninFig.2.13. By writing the gradient of
c
as (∂
c
/∂
c)(∂
c/∂x
k
) and noting the
typical behaviours of these two gradients, one observes that turbulent flux is counter-
gradient in high-Da and small-Le flames. A strong flame-normal acceleration that
is due to greater heat release in the low-Le as well as in the large-Da flames acts
to promote counter-gradient transport, and the magnitude of the flame-normal ac-
celeration decreases with either increasing Lewis number or decreasing Damkohler
number, promoting gradient transport. This is evident from the DNS results shown
in Fig. 2.13.

88 Modelling Methods
(
a
)(
b
)(
c
)
Figure 2.13. Variations of turbulent flux ρ u
1
c
in statistically planar turbulent premixed
flames of (a) high Da (Da = 6.84, Ka = 0.54, Re
T
= 56.7, τ = 2.3, Le = 1), (b) low Da
(Da = 0.32, Ka = 13.2, Re
T
= 47, τ = 4.5, Le = 1.0); (c) Da = 0.32, Ka = 13.2, Re
T
= 47,
τ = 4.5, Le = 0.34. These flames are studied in [193] and have a Zeldovich number of 6.0.
Further analyses [193] revealed that the counter-gradient transport for the tur-
bulent flux is observed when the scalar flux
ρ u
c
is counter-gradient. Earlier studies
by Veynante et al. [1] and Chakraborty and Cant [194] also demonstrated that the
turbulent transport of a scalar gradient is closely related to the scalar flux in premixed
flames. Following these studies, a model for
ρ u
1
c
is proposed as [193]
ρ u
1
c
=
ˆ
A
(
" −
c
)
ρ u
1
c
&
c
2
+
c(1 −
c)
'
c
, (2.109)
where
ˆ
A = 2 and " = 0.5 are model parameters. A typical performance of this model
is compared with the DNS result in Fig. 2.13. It is evident that this model captures the
counter-gradient as well as gradient transport without any modification to the model
parameters,
ˆ
A and ". The quantitative agreement between the model prediction and
the DNS data is satisfactory. It is to be noted, however, that proper modelling of the
scalar flux
ρ u
1
c
is required, which will be discussed later (see also Section 2.1).
MODELLING OF SCALAR–TURBULENCE INTERACTION. The sum of three terms, (V) +
(VI) + (VII) in Eq. (2.90), is collectively called the scalar–turbulence interaction
term because they originate from T ≡−
2 ρ ˆα∂c/∂x
(∂u
/∂x
k
) ∂c/∂x
k
, which is the
averaged form of the second term on the right-hand side of Eq. (2.89). This term
signifies the interaction of turbulence and scalar gradients, and it is to be noted that
only the symmetric part, e
k
≡ 0.5(∂u
/∂x
k
+ ∂u
k
/∂x
), of the strain tensor ∂u
/∂x
k
is involved because the contribution of the rotational part R
k
to T is exactly zero.
Using eigendecomposition, one writes
T =−
2 ρ N
c
(e
α
cos θ
α
+ e
β
cos θ
β
+ e
γ
cos θ
γ
), (2.110)
where e
α
, e
β
, and e
γ
are the eigenvalues of e
k
ordered as e
α
> e
β
> e
γ
,withe
γ
being
the most compressive principal strain rate; the three eigenvalues are orthogonal to
one another. It is apparent that the statistical behaviour of T is governed by the statis-
tics of the alignment angles, denoted previously by θ, between the scalar-gradient
vector and directions of the principal strain rates. It is well known that the scalar
gradient aligns most probably with the compressive strain rate e
γ
in cold turbulence
[195–200] and even in flows with passive chemical reactions [203, 204] (without dilata-
tion). This situation, shown schematically in Fig. 2.14(a), implies that the turbulence
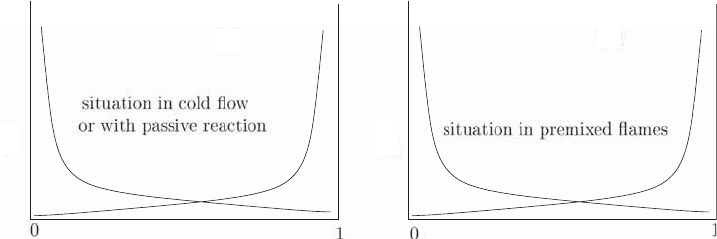
2.3 Scalar-Dissipation-Rate Approach 89
e
α
e
α
e
γ
e
γ
|cos θ|
(a) (b)
|cos θ|
PDF
PDF
Figure 2.14. Schematic of scalar-gradient alignment with the most extensive and compressive
principal strain rates e
α
and e
γ
, for (a) passive scalar mixing in a turbulent flow and (b) reactive
scalar in a premixed flame.
produces scalar gradients by bringing isoscalar surfaces together and this production
is balanced by the molecular-diffusion process. When there is strong heat release, the
dilatation usually occurring in the local normal direction overwhelms the turbulence
effects, resulting in alignment PDFs shown in Fig. 2.14(b) for premixed flames –
the scalar gradient aligns most probably with the most extensive strain rate, e
α
,re-
sulting in the destruction of the scalar gradient by the turbulence [168, 186–189].
This destruction, aided by the molecular diffusion, balances the production of scalar
gradients by chemical reactions. As one can see, this is different from the passive
scalar or cold-flow scenario, and it is important to understand and to account for the
change in physics for correct modelling of turbulent premixed flames.
The local production or destruction of scalar gradients by the turbulence is
determined by the competing effects of heat-release-induced straining and turbu-
lence straining. The former is related to the dilatation rate, which scales as a
chem
≡
∂u
/∂x
∼ τ f (Le) S
0
L
/δ
0
L
, and the turbulent strain rate scales as a
turb
≡ u
rms
/.A
function of the Lewis number is included to account for the non-unity Le effects
[168] on dilatation, and its specific form, introduced later, is not important at this
time. However, it is worth noting that this function should take a value of unity for
Le = 1 to be consistent with the classical scaling, and it increases with decreasing Le
[168]. The ratio of these two strain rates is a
chem
/a
turb
∼ τ f (Le) Da
L
, where Da
L
is
local Damk
¨
ohler number. Because t he turbulence involves a r ange of scales, one can
also use the Kolmogorov time to scale the turbulent strain rate. If one uses this time
scale, then a
chem
/a
turb
∼ τ f (Le)/Ka
L
, where Ka
L
is the local Karlovitz number. One
has a
chem
/a
turb
1 when the heat release effects are dominant, resulting in the scalar
gradient aligning with the extensive strain rate e
α
. This happens when (1) τ is large,
(2) Le is small, (3) the local Damk
¨
ohler number is large, and (4) the local Karlovitz
number is small. All of these conditions, except (2), are met, even for Le ≥ 1 flames
when the combustion is in the corrugated-flamelets as well as wrinkled-flamelets
regimes, which are signified by Da 1 and Ka < 1 (see Fig. 1.3). Physically, in these
regimes the flame scales are smaller than typical large and small scales of turbulence.
The alignment characteristics shown in Fig. 2.15(a) for this situation indicates that
the turbulence dissipates the scalar gradient. On the other hand, one expects the
turbulence to produce the scalar gradients when Da < 1 and Ka > 1 because the

90 Modelling Methods
(
a
)
PDF
(
b
)(
c
)
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
Figure 2.15. PDF of scalar-gradient alignment angle with the most extensive principal strain
rate e
α
in the flames considered in Fig. 2.13.
turbulence straining dominates the dilatation-induced straining, but the DNS results
in Figs. 2.15(b) and 2.15(c) show that the heat release effects dominate the turbulence
locally in the regions of intense heat release. For Da > 1 and Ka > 1 conditions, one
may argue that the turbulence dissipates the s calar gradient because Da > 1byjust
considering the large scales of turbulence. But Ka > 1 implies that the small-scale
fluid dynamic processes are faster than the chemical reaction and thus the align-
ments may be those of a passive scalar situation. It seems that the bulk behaviour
of the turbulence–scalar interaction will be determined by the preponderance of
one of these competing processes at different scales. Experimental investigation by
Hartung et al. [189] showed that the scalar gradient aligns with the most extensive
strain rate even in laboratory flames with Da > 1 and Ka > 1. Although results for
statistically planar flames with unity and non-unity Le flames are shown here, a de-
tailed analysis [205] of flame kernels (curved flame brushes) showed that the scalar
gradients are likely to align with the most extensive strain rate when the local heat
release effects are strong.
Out of the three terms of turbulence–scalar interaction, (V) and (VII) are influ-
enced by the alignment characteristics previously discussed. One can note from the
preceding discussion that the alignment characteristics are influenced by both Da and
Ka. Thus the modelling of these terms should explicitly include Da and Ka to cap-
ture the heat release effects; such models were developed in [168, 191, 193, 205]. In
the following these models are briefly discussed, highlighting their salient features,
and the readers are referred to appropriate works for further details. However,
the information provided here is sufficient for model calculations using the SDR
approach.
The predominant contribution to the turbulence–scalar interaction term, i.e., the
sum (V) + (VI) + (VII), comes from (VII) when the thermochemical or heat release
effects are significant. The contributions of (V) and (VI) are likely to be important
in low-Da combustion. These observations are noted in [168, 186, 191, 192, 205].
Modelling of (V)
Mantel and Borghi [165] proposed a model for (V) as
(V) ∼−
ρ
u
c
t
scal
∂
c
∂x
−C
P
c
ρ
u
c
ε
k
∂
c
∂x
, (2.111)

2.3 Scalar-Dissipation-Rate Approach 91
with
k and ε denoting the turbulent kinetic energy and its dissipation rate, respec-
tively, and the model constant C
P
c
is of the order of unity. The time scale t
scal
is taken
to be the turbulence time scale τ
T
. This model notes a direct relationship between
the scalar flux and (V), which was noted in a number of DNS studies under a variety
of flame and flow conditions [191–193, 205]. However, if one follows the arguments
[1] behind Eq. (2.22) then the scalar flux can be expressed as
u
c
≈
(
2 α u
rms
− τS
L
)
c(1 −
c)M
, (2.112)
where α is an appropriate efficiency function and M
is the component of the unit
normal vector of
c field pointing towards the reactant side. After substituting this
expression into relation (2.111), one sees that the resultant expression has scalings
O(ρ
u
c
2
u
2
rms
/
2
;Re
0
T
) and O(ρ
u
c
2
S
0
L
2
/δ
0
L
2
;Re
−1/2
T
Da
−3/2
) for the non-reacting and
reacting parts, respectively. The scaling of the non-reacting part is consistent with
that in Eqs. (2.93) but that of the reacting part is not consistent with Eqs. (2.108).
This is because the turbulent time scale is also used to represent t
scal
in the reactive
regions. Clearly this is inadequate because the heat release affects the turbulence–
scalar interaction, as previously discussed, and also it is inconsistent with the scalings
suggested in [150]. Thus the preceding model is revised [191, 192]as
(V) −
[
C
1
+ C
2
Da
∗
L
]
ρ
u
c
ε
k
∂
c
∂x
, (2.113)
where Da
∗
L
≡ ρ
u
Da
L
/ρ is the density-weighted local Damkohler number and
the density weighting is used to minimise the effect of the kinematic viscosity
change that is due to heat release on ε. The model parameters are C
1
= 0.5 and
C
2
= 1.3Ka
2
L
/(1 + Ka
L
)
2
. The second term involving C
2
inside the square brackets
accounts for the contributions from the reacting r egions, and it explicitly includes
the local Damk
¨
ohler and Karlovitz numbers to account for the heat release effects
on the turbulence–scalar interactions. This is because δ
0
L
/S
0
L
is used to represent the
time scale t
scal
. This model is noted to work well in [192] and [191] for high- and
low-Da flames without having to alter the numerical values of the model parameters
C
1
and C
2
.
Local flame propagation is strongly influenced by the TD instability in non-
unity Le flames and also by the flame stretch effects induced by flame straining
and bending. Flame straining by turbulence is already included in relation (2.113).
Although this model qualitatively predicts (V) in non-unity Le cases satisfactorily
[168], its quantitative predictions may be improved by including Le effects on flame
straining by use of f (Le), as noted earlier. This gives a model
(V)
&
ˆ
C
1
+
ˆ
C
2
f (Le) Da
∗
L
'
ρ
u
c
ε
k
∂
c
∂x
; (2.114)
alternative ways are also available [193]. The flame-curvature-induced stretch effects
can be included [205] following the Markstein diffusivity analogy [56][seeEq.(3.1)
also] for curved flames. The turbulent scalar flux expression given in relation (2.112)
can be written as
u
c
≈
(
2 α u
rms
− τS
L
)
c(1 −
c)M
, (2.115)

92 Modelling Methods
where a modified flame speed S
L
= S
0
L
−
ˆ
D∂M
/∂x
is used, with
ˆ
D as an appropriate
diffusivity to include the mean-curvature effects. Now, some algebraic rearrange-
ments yield
(V) −
[
C
1
+ C
2
Da
∗
L
]
ρ
u
c
ε
k
∂
c
∂x
+
ˆ
ˆ
C
2
ρτDa
∗
L
c(1 −
c)
ε
k
∂
c
∂x
ˆ
D
∂M
∂x
. (2.116)
This relation becomes relation (2.113) for statistically planar flames because the last
term in relation (2.116) becomes zero. This model is shown in [205] to capture the
variations of (V) in kernel DNS satisfactorily with
ˆ
ˆ
C
2
≈ 1.0.
Mura et al. [176] recently proposed the following models:
(V) =−C
M
ρ
c
c
2
u
c
∂
c
∂x
,
=−τ S
L
ρ
c
−→
n
f
·
−→
x
∂
˜
c
∂x
, (2.117)
where C
M
is a model constant of the order of unity, n
f
is the local flame-normal
vector, and the average value of the direction cosine is taken to be 0.8. If one uses
the scaling
c
∼
c
2
ε/
k then the first of the two models in Eqs. (2.117) becomes
similar to that in relation (2.111). These two models perform satisfactorily for high-
Da flames considered by Mura et al. [176]; however, their performance for low-Da
combustion is yet to be assessed. One shall recall an earlier observation that the
contribution of (V) in high-Da flames is negligible, and it is likely to be important in
low-Da situations.
Modelling of (VI)
Mantel and Borghi [165] proposed a model for this term as
(VI) −C
P
U
ρ
c
u
u
k
k
∂ u
∂x
k
. (2.118)
The scaling estimate for this model is consistent with the order-of-magnitude estimate
in Eqs. (2.108), but it relates gradients of scalar fluctuation to the Reynolds stress
with an assumption
H
k
≡
ρD
ρ
c
∂c
∂x
∂c
∂x
k
u
u
k
2
k
, (2.119)
which is unclear. Recently, a proposition [192] that is similar to the concept of the
Cant, Pope, and Bray (CPB) model [206] for surface averages of the products of the
flame-normal components,
(n
n
k
)
s
= n
n
k
|
∇c
|
/, appearing in the FSD approach
is made as
H
k
= ψ
ψ
k
+
1
3
δ
k
(1 − ψ
m
ψ
m
), where ψ
k
=−
∂
c
∂x
k
,
ρ
u
D
u
ρ
c
. (2.120)
The Reynolds average of Favre fluctuations is
c
= c −
c = τ
c(1 −
c)/(1 + τ
c) when
the combustion occurs in thin flamelets, and the PDF of c can be approximated as
