Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames
Подождите немного. Документ загружается.

3.1 Instabilities in Flames 163
Δ
time (s)
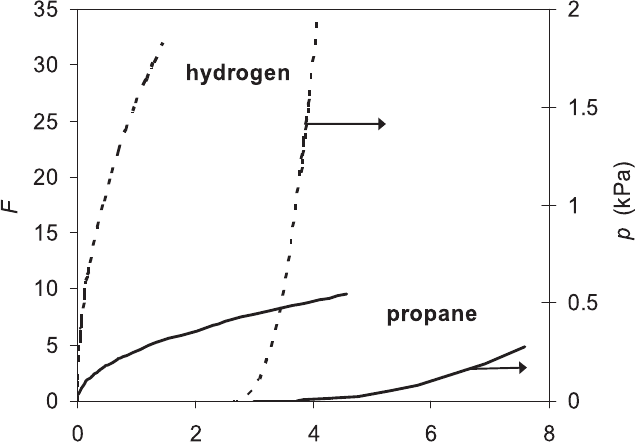
Figure 3.9. Computed F and p 1 km from the centre of the fireball for large spherical
atmospheric explosions of hydrogen (broken lines), φ = 0.5 and propane–air (solid lines),
φ = 1.06, up to maximum radii of 100 m.
for the propane–air flame, φ = 1.06, that was studied in the large-scale experimental,
atmospheric explosions of [22]. Relevant properties are Ma
sr
= 5.5, u
= 0.41 m/s,
B = 0.242, σ = 8.303, and
ˆ
c = 333.7m/s. The computed values of F and p are
plotted against the time from the onset of the instability by the solid lines in Fig. 3.9.
The time lag in the arrival of the pressure pulse is apparent. Values of p are for
a distance of 1 km from the centre of the fireball. The computed flame radii extend
to a maximum of 100 m, when the flame terminates. With σ = 8.303, for this radius
of a completely burned mixture, the original radius over which the initial unburned
mixture extended, prior to ignition, would be 49.4 m. The maximum computed
pressure of about 0.3 kPa is not severely damaging, although it would be higher
closer to the flame and is rising rapidly as the flame propagates. It is close to a value
at which glass windows would fail. In the experiments of [22], the maximum flame
radius was 3.75 m after 0.51 s.
In contrast, the broken lines give computed values of F and p in an atmospheric
explosion of a more unstable mixture of hydrogen–air, φ = 0.5, Ma
sr
=−8, u
=
0.65 m/s[6], B = 0.59, σ = 5.01, and
ˆ
c = 379.8m/s. Again, the maximum flame
radius was 100 m and d was 1 km. This explosion is more rapid, with F reaching a
maximum value of 32 and p one of about 2 kPa. Clearly, larger explosions would
be even more damaging and there is no apparent limit to the acceleration of large
unstable fireballs, other than that provided by an increasing radiative energy loss
from the burned gases [22]. This is an area worthy of further study.
RAYLEIGH–TAYLOR INSTABILITIES. The pressure waves generated by DLTD insta-
bilities can create additional instabilities and overpressures. Taylor instabilities
164 Combustion Instabilities
arise when pressure gradients are aligned orthogonally to the high-density gra-
dients at the flame surface, with vorticity generation by means of the baroclinic
term, ∇(1/ρ) ×∇p [25]. Markstein [26] demonstrated this instability by wrinkling
a smooth spherical laminar flame surface with an impacting shock wave. When the
planar pressure pulse hit the sphere, it accelerated the lower-density burned gas
preferentially. This phenomenon was also observed in vented explosions [14, 27]
and flame propagation along tubes [28], where it can produce large increases in the
burning rate. The Rayleigh instability occurs when the combustion energy release
feeds directly into the positive phase of a pressure wave, amplifying it according
to Rayleigh’s [29, 30] criterion: The amplitude of an acoustic wave will increase if
heat is added in phase with the pressure. The Rayleigh source term
p
q
dV [see
Eqs. (3.39) and (3.40)] in the acoustic energy equation can be highly destabilising,
and the unsteady rate of heat release arising from fluctuations in φ during the com-
bustion of lean premixtures also can affect the oscillation frequency [31]. In practice,
Rayleigh–Taylor thermoacoustic instabilities are usually coupled and are hereafter
designated by RT. The thermoacoustic instabilities and their control strategies and
simulation methods are discussed in Sections 3.2 and 3.3, respectively.
Confined and semiconfined flames create overall increases in pressure and gen-
erate pressure waves that reflect at containing walls. Transitions between different
instabilities in confined explosion flames were studied in an explosion bomb of 385-
mm diameter with three pairs of orthogonal windows of 150-mm diameter [32].
Simultaneous ignition at two diametrically opposite sparks at the wall of the bomb
created two near-identical imploding flames that could be viewed at the central win-
dow. The advantage of this configuration was that the flames propagated at higher
pressures and Peclet numbers than would have been possible with central ignition.
The technique was used to measure laminar burning velocities at high pressures in
[33]. Some experimental results from [32] for explosions of three different mixtures,
initially at 0.5 MPa and 358 K but with different degrees of instability, are presented
in Table 3.1. These values were measured at the maximum values of u
c
.Thethree
mixtures ranged from a relatively stable stoichiometric i-octane–air mixture to a very
unstable rich mixture, φ = 1.6, of the same gases.
It was possible to explain the maximum enhanced burning velocity
(
u
c
)
max
of the
first and most stable stoichiometric mixture entirely in terms of DLTD instabilities
after Pe
cl
was attained. The value of p was too small to be measured. Values of
F were found from Eqs. (3.14) and (3.16) and of u
c
from Eq. (3.19). The second
mixture was of H
2
–air with φ = 0.4, and this created a small primary thermoacoustic
instability, with p = 0.8 kPa at
(
u
c
)
max
.AfterPe
cl
was attained, burning velocities
initially could be attributed entirely to DLTD instabilities until just after the onset of
flame oscillations, when the associated cellularity began to decline. The oscillations
developed in tandem at both of the imploding flames and seemed to cause the
reduction in both flame cellularity and u
c
.
These changes are explained by reference to Fig. 3.2. The Taylor effect suggests
that, with this configuration, a pressure higher on the unburned than on the burned
side, the leading edge of burned gas would be preferentially accelerated towards
the burned gas, reducing the cellularity. Conversely, with a higher pressure on the
burned side, the same leading edge of burned gas would be preferentially accelerated
towards the unburned gas, now increasing the cellularity. Thus the Taylor generation
of vorticity can either stabilise or destabilise the flame. Laser-sheet observations and

3.1 Instabilities in Flames 165
Table 3.1. Summary of experimental findings [32] at maximum u
c
, with all values for this
condition. PA is primary acoustic and SA is secondary acoustic oscillations. estimated value,
RT
s
is Rayleigh-Taylor stabilisation
pT u
at (u
c
)
max
F at p at Type of
Mixture (MPa) (K) (u
c
)
max
(m/s) Ma
sr
(m/s) (u
c
)
max
(u
c
)
max
(kPa) instability
i-C
8
H
18
–air 1.8 502 0.295 2 0.66 2.2 0 DLTD
φ = 1.0
H
2
–air 0.97 440 0.34 −11 2.19 6.4 0.8 DLTD,
φ = 0.4 PA, RT
s
i-C
8
H
18
–air 2.06 508 0.10 −20
∗
3.75 37.5 300 DLTD,
φ = 1.6 RT , PA
SA
the changing values of u
c
suggest the stabilising, or laminarising, tendency to be
the stronger, with initially a pronounced reduction in cellularity. Subsequently this
was followed by the development of a ‘finger-like’ surface structure. Particle image
velocimetry also showed that, with unburned-gas flow into the flame surface, the
surface was smoothed and with the flow away from the surface it tended to form the
finger-like structure [32]. Kaskan [34] observed similar stabilising and destabilising
area changes in near-flat flames propagating along a tube and subjected to pressure
oscillations of small amplitude. Later experiments showed cellular flames to be
laminarised by low-intensity primary acoustic oscillations with a maximum p of
about 0.5 kPa during flame propagation along an open tube [35].
There is no such effect with the more severe, secondary thermoacoustic oscilla-
tions generated in the third, highly unstable, rich iso-octane–air mixture in Table 3.1.
This is clearly manifest as a severe secondary thermoacoustic instability, encouraged
by a very negative Ma
sr
and triggered by the original DLTD instabilities. It yields
high values of p = 300 kPa and of F = 37.5at
(
u
c
)
max
. The values of u
c
are more
than five times greater than those predicted for DLTD instabilities alone. This and
the high value of p confirm the generation of strong RT instabilities, which are
often referred to as thermoacoustic instabilities. These are addressed in detail in the
following two sections of this chapter.
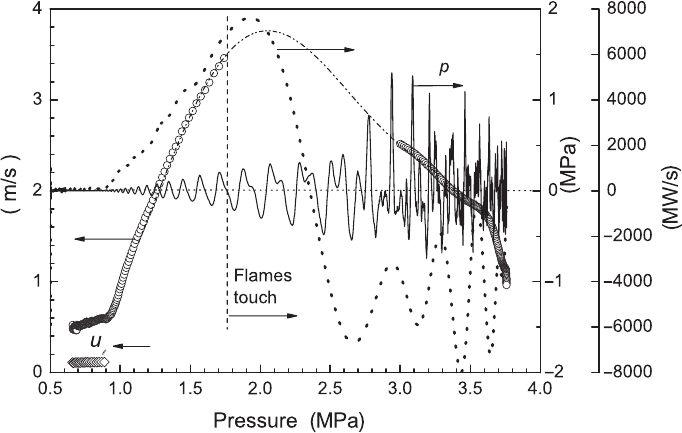
Figure 3.10 shows the developing amplitude of the pressure oscillations as the
pressure rises, as well as increases in u
c
and the changing rate of change of the heat
release rate. In the initial stages of the DLTD instabilities, the theory of the earlier
subsection on the peninsula of instability was able to predict the values of u
, indi-
cated by the diamond symbols. This instability seeded the RT instabilities through
the rate of increase of u
and associated increase in p, which further increased
values of u
c
. The further growth of p provided a powerful feedback mechanism
for further increases. Diagrams similar to Fig. 3.10 are provided in [32] for the other
two mixtures of Table 3.1.
In flame propagation from the end of a closed tube, pressure waves are generated
by the impulsive start to flame propagation at the closed end. These were analysed
numerically in [36]. A leading shock was found to be reflected at the open end and
the reflected wave then reflected at both ends, generating an increasingly complex
sequence of reflections. With high burning velocities, a rapid acceleration to a high
flame speed generates higher values of p in secondary thermoacoustic oscillations.
166 Combustion Instabilities
Δ
Δ
p
u
n
Figure 3.10. Changes in u
c
(u
n
in figure) and pressure oscillations during inward propagation
of two near-simultaneous i-octane–air, φ = 1.6, flames. The dotted curve shows the rate of
change of heat release rate [32].
Experiments showed that high flame speeds eliminate reversals in the direction of
flame propagation that arise from the interaction of the flame with the oscillating col-
umn of gas at lower flame speeds [37]. These reversals led to the laminarisation of the
flame. At the higher flame speeds, secondary thermoacoustic instablities with higher-
pressure amplitudes p of up to 20 kPa ultimately destroyed the cellular structure.
This was succeeded by one more akin to that of a highly turbulent flame, with a
burning velocity many times greater than the laminar burning velocity [35]. Theo-
retically, Bychkov [38] and Aldredge [39] identified a range of acoustic amplitudes
in which flames are stabilised by primary acoustic velocity oscillations. This regime
is intermediate between those of primary and secondary thermoacoustic instabilites.
Unconfined flames also can be subjected to RT intabilities, arising from the
generation of oscillations in the burner manifold ahead of the flame. Strong noise
can radiate because of the acoustic–combustion coupling between the flame and
the manifold’s resonant modes. For the configurations considered in [40], pressure
perturbations in the manifold were almost in phase with perturbations of the heat
release rate. The power generated by the Rayleigh source term minus the small
damping losses in the system determined the acoustic radiation to the far field,
which is explored more in Section 3.2.
3.1.2 Turbulent Burning, Extinctions, Relights, and Acoustic Waves
When mild velocity fluctuations are imposed on an unstable laminar flame, the burn-
ing velocity enhanced by instabilities persists [41, 42]. Paul and Bray [43] developed
a flamelet model for moderately turbulent combustion, based on the numerical sim-
ulations in [41]. It accounts for the persistence of DLTD instability, together with
stretch rate and Markstein number effects. The predicted burning velocities are in
good agreement with experimental measurements. As the spectrum of turbulence

3.1 Instabilities in Flames 167
develops with an increasing rms turbulent velocity u
rms
, the length scales increas-
ingly subsume those of the original unstable wavelengths. In the experiments in [32]
this process seemed to be completed at about u
rms
/u
= 3 and the original pressure
fluctuations that are due to instabilities largely disappeared. At higher turbulence
intensities, values of Markstein numbers continue to influence the burning rate and
flame extinction [44].
A practical definition of the turbulent burning velocity u
t
is that when multiplied
by the unburned-gas density and the appropriate flame area it gives the mass rate at
which burned gas is formed. Defining this area is problematic because of the very
different flow geometries in the various burners and explosion bombs that are used
to measure u
t
. In addition, as correlations involve u
rms
, this should be the same
over the entire flame surface. Vital information on the turbulent flame bush can be
revealed by laser-sheet measurements of the distribution of reactants, products, their
interfaces, and the mean reaction progress variable
c. Values of c have been used to
define appropriate flame surface areas for u
t
[45–47]. Further progress on this topic
is discussed in Section 2.3.
An earlier correlation of experimental turbulent burning velocities expressed
u
t
/u
rms
as a function of the turbulent Karlovitz stretch factor K and Le [48]. For
isotropic turbulence, K is based on the rms strain rate on a randomly orientated
surface, u
rms
/λ, where λ is the Taylor scale of turbulence. When normalised by the
chemical time, δ
/u
, this gives
K =
u
rms
δ
λ u
. (3.23)
With δ
approximated by ν/u
and λ related empirically to the integral length scale
by λ
2
/ = A
ν/u
rms
, where A
is an empirical constant, here assigned a value of
16, Eq. (3.23) gives
K = 0.25 Re
−1/2
T
u
rms
u
2
, (3.24)
where Re
T
is the turbulent Reynolds number based on .
When the flame surface area of spherical explosion flames is defined by a surface
at which the mean reaction progress variable is
c, the associated burning velocity
measured u
tc
in the isotropic turbulence of a fan-stirred bomb was correlated by [47]:
u
tc
u
rms
= A
c
α K
β
, (3.25)
in which A
c
is a constant that is dependent solely on the surface selected to define
the turbulent burning velocity based on the mass rate of burning. For the surface at
which the mass unburned behind it is equal to the mass burned ahead of it, A
c
is
unity and
c is usually close to 0.59. For a leading edge with c = 0.05, the value of A
c
is 0.75. Values of α and β are expressed by first-order equations in Ma
sr
:
α =
/
0.022
(
30 − Ma
sr
)
for + ve Ma
sr
0.0311
(
30 − Ma
sr
)
for − ve Ma
sr
,
β =
/
0.0105
(
Ma
sr
− 30
)
for + ve Ma
sr
−0.0075
(
Ma
sr
+ 30
)
for − ve Ma
sr
. (3.26)
168 Combustion Instabilities
A limit to the ever-increasing turbulent burning velocity with u
rms
is provided by
localised flame extinctions at sufficiently high values of K [49].
Flame-extinction stretch rates in laminar flow at different φ were obtained with
experimental opposed jet flames. Values are plotted in Fig. 3.1 by the solid lines for
C
3
H
8
and CH
4
[50] and H
2
[51], with air, under atmospheric T and p. The high values
for lean H
2
mixtures are particularly noteworthy. When turbulent flames make very
brief, localised excursions into stretch rates that are higher than those that would
extinguish a laminar flame, they do not necessarily extinguish [52]. Because of this
apparent time lag and other theoretical complexities [44], data on turbulent flame
quenching are best found experimentally. The probability of an initial flame kernel
continuing to propagate, p
f
, was measured in fan-stirred bombs at different rms
turbulent velocities, u
rms
. These experiments were with mixtures of CH
4
,C
3
H
8
, and
i-octane with air and very lean H
2
–air mixtures, all in the pressure range 0.1–1.5 MPa
and at room temperature. Values of K for probabilities of 0.8 and 0.2 were expressed
in terms of Ma
sr
by [49]
K
0.8
(
Ma
sr
+ 4
)
1.8
= 34.4forp
0.8
, (3.27a)
K
0.2
(
Ma
sr
+ 4
)
1.4
= 37.1forp
0.2
, (3.27b)
for −3.0 ≤ Ma
sr
≤ 11.0. Values of K
0.8
are plotted against Ma
sr
in Fig. 3.6.
Localised turbulence-induced extinctions followed by relights emerge as a prob-
lem when lean hydrocarbon–air mixtures are leaned off in low-NO
x
burners. The
associated rapid changes in dV/dt can induce pressure oscillations with frequencies
as high as 100 Hz [53]. A combined computational and experimental study of pre-
mixed turbulent combustion of CH
4
–air in a swirl burner showed a region of high
stretch rate between inner and outer recirculation zones [54]. As the mixture was
leaned off and K increased, reaction in this region was locally extinguished at about
φ = 0.59. However, reaction continued elsewhere, stabilised by the hot gas in an
inner recirculation zone in a different flame configuration. Video films revealed os-
cillations at a frequency of about 20 Hz between the two quasi-steady solutions with
the generation of acoustic waves. With a further reduction in φ, the redistribution of
strain rates generated a final flame configuration, after which further reduction in φ
below 0.56 extinguished the flame completely.
In another important area, localised flame extinctions by high stretch rates limit
the continuing acceleration of runaway turbulent flames in ducts with turbulence-
inducing obstacles. Under these conditions, the turbulent burning velocity attains a
maximum value [55]. If this and the generated shock waves [36] are high and strong
enough to auto-ignite the unburned mixture between the shock wave and the flame,
a transition from deflagration to detonation can ensue [55].
3.1.3 Auto-Ignitive Burning
AUTO-IGNITIVE PROPAGATION VELOCITY. Where the intended combustion mode is
either a premixed laminar or turbulent flame, a stochastic transition to auto-ignitive
burning can be perceived as an instability. A familiar example is knocking combustion
in a gasoline engine. Efficient engine operation, with a high burn rate on the fringe
of severe knock, can be nullified by occasional cyclic excursions into such a knock
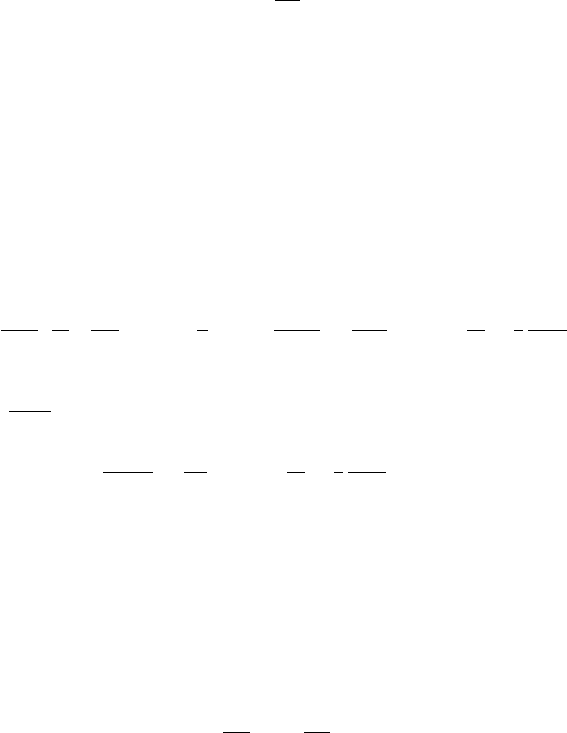
3.1 Instabilities in Flames 169
as a result of the sensitivity of auto-ignition to comparatively small changes. In
laminar and turbulent flames, molecular-transport processes are integral parts of the
mechanism of flame propagation. This is not the case with auto-ignition.
In a homogeneous mixture, auto-ignition manifests itself as a spontaneous re-
action throughout the mixture, without any propagating front and occurs after the
auto-ignition delay time τ
i
has elapsed. Where there are spatial gradients of τ
i
in
a radial direction r, because of those of either T or φ, or both, an auto-ignition
propagation velocity can arise, given by
u
a
=
dr
dτ
i
. (3.28)
When u
a
is close to the acoustic velocity
ˆ
c, the two can become coupled in a
strong shock wave, with the creation of a new entity, a detonation wave, with a
distinctive high-pressure peak and a very high detonation velocity. An important
parameter is the ratio ξ =
ˆ
c/u
a
. Because of inevitable inhomogeneities in mixtures,
auto-ignitive propagation usually originates at a hot spot at which the initial radius
of the hot spot must exceed the critical radius given by thermal-explosion theory
[56]. This condition is usually satisfied in engines. The rate of change of the rate of
volume generation again generates pressure waves, as given by Eq. (3.17).
From Eqs. (3.17) and (3.20), with r equal to the radius of an auto-ignitively
propagating spherical hot spot, replacing u
c
with u
a
, and with ξ =
ˆ
c/u
a
,
p(t) =
ρ
4π d
d
dt
dV
dt
t−t
d
=
ρ
d
(σ −1)
dr
2
u
a
dt
=
ρrc
2
d
(σ −1)
2r
ξ
2
+
r
ˆ
c
dξ
−1
dt
t−t
a
.
(3.29)
With
ˆ
c =
√
γp/ρ,Eq.(3.29) becomes
p(t)
p
=
r γ
d
(σ −1)
2r
ξ
2
+
r
ˆ
c
dξ
−1
dt
t−t
d
. (3.30)
The last term within the square brackets, unlike that with unstable flames, is likely
to be relatively small, and the fractional pressure increase that is due to the auto-
ignition, characterised as knock, is inversely proportional to ξ
2
. This can be as high as
0.4MPaat1.4 MPa for a single hot spot [57]. To derive this magnitude requires values
of u
a
. These can be found most conveniently if the mixture composition is assumed
uniform and the gradient of reactivity arises entirely as a temperature gradient. In
that case, Eq. (3.28) can be re-expressed as
u
a
=
∂T
∂r
−1
∂τ
i
∂T
−1
. (3.31)
Values of τ
i
(
T, p
)
differ between different fuels and change in different ways
with T and p . This is illustrated by the plots of τ
i
(
T, p
)
, at the indicated pressures,
against 1000/T in Fig. 3.11, taken from [58]. Four of the curves are for primary ref-
erence fuels (PRFs), which are used in attempts to simulate the knocking behaviour
of gasolines. The octane number, ON, is the percentage by volume of i-octane mixed
with n-heptane in a PRF. Only at the high temperatures in Fig. 3.11 do they exhibit
a similar straight-line Arrhenius relationship to the other three fuels. The variation
with pressure is an inverse one, expressed by p
−n
, where n is a pressure exponent.
170 Combustion Instabilities
Figure 3.11. Ignition delay times τ
i
(T, p) of various fuels with air at φ = 1.0, unless otherwise
stated. See [58] for source references.
It has a value of about 1.7 for PRFs and one closer to unity for many non-PRFs,
for T < 1000 K [59]. At higher temperatures, values of τ
i
(
T, p
)
become closer for
different PRFs.
Values of ∂τ
i
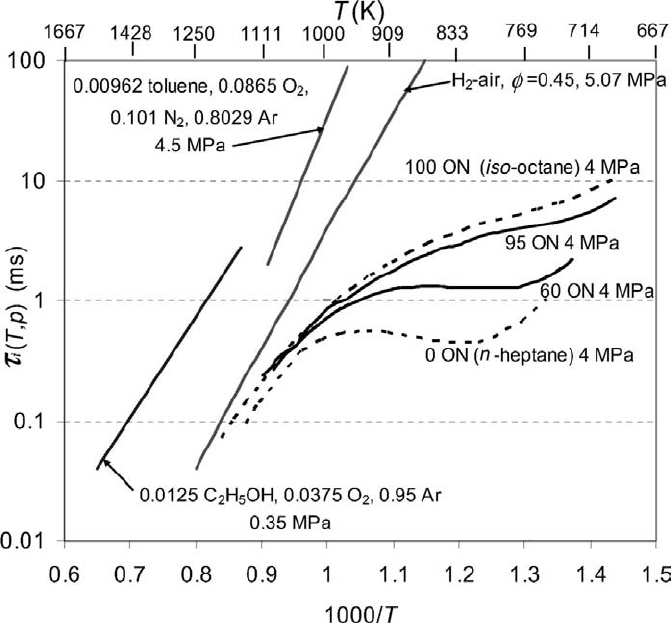
/∂T were derived for the PRF with ON = 60 for a stoichiometric
mixture at 4 MPa from the τ
i
versus 1/T data in [60]. To obtain u
a
, it is necessary
to assume a value of ∂T/∂r. Temperature gradients arise at cooled surface boundary
layers and, in the body of the charge, due to turbulence. An assumed value of
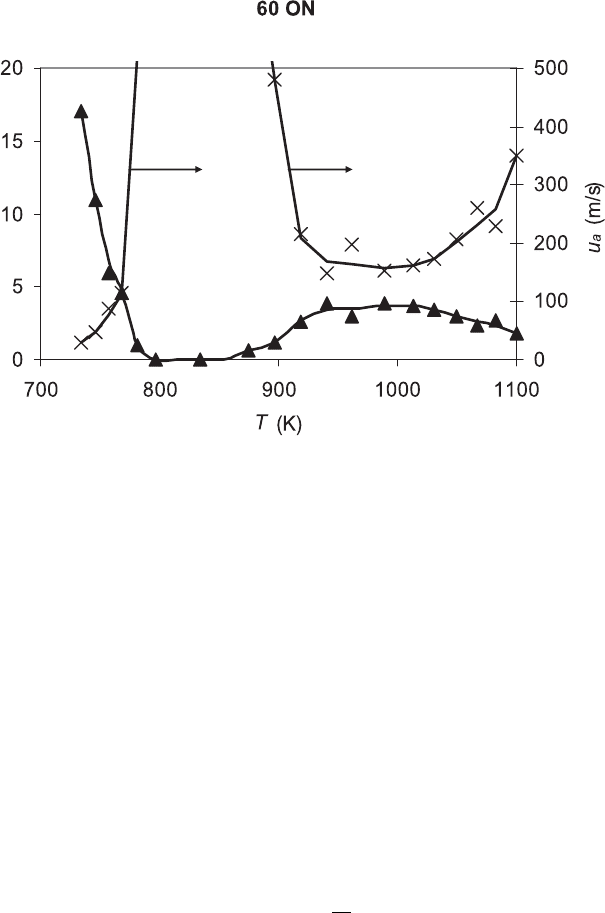
∂T/∂r =−1K/mm gave the values of u
a
shown by the cross symbols in Fig. 3.12
and, from the corresponding values of
ˆ
c, it also gave those of ξ. The 60 ON curve
in Fig. 3.11 shows a region where ∂τ
i
/∂T is close to zero between about 800 and
860 K, which implies an infinite value of u
a
and ξ = 0. It is apparent from Fig. 3.11
that, for the PRFs, ∂τ
i
/∂T increases numerically with ON. Hence u
a
will decrease and
ξ will increase. Clearly, from Eq. (3.30), low values of ξ imply large values of p(t)/p,
and severe knock would be anticipated for the conditions of Fig. 3.12 in a gasoline
engine. It would become less severe at about 950 K, but severe high-temperature
knock would begin to develop above 1100 K.
The computations of u
a
are for the given initial boundary conditions of T and
p. In practice, these correspond best to auto-ignitions in shock tubes and rapid-
compression machines. For slower compressions in engines when auto-ignition is
3.1 Instabilities in Flames 171
ξ
Figure 3.12. Variations of ξ and u
a
with temperature at 4 MPa, stoichiometric 0.60 i-octane,
0.40 n-heptane, and air, derived from τ
i
values in [55], dT/dx =−1K/mm. From [58].
not completed at fixed values of T and p , the mixture will have partially reacted
during compression. Consequently the mixture will auto-ignite rather more rapidly
than is suggested by the tabulated values of τ
i
for T and p. With a reduced effective
τ
i
in Eq. (3.31), u
a
would be increased.
MODES OF AUTO-IGNITION. A value of ξ close to unity is particularly significant
because it suggests a resonance between the acoustic speed
ˆ
c of the pressure wave
and the propagation velocity u
a
of the auto-ignitive front. The auto-ignition delay
time is followed by a much shorter excitation time τ
e
, during which most of the heat
release rate occurs [61]. A high rate of chemical heat release at small τ
e
, continually
feeding into the pressure front, will reinforce the front and increase the probability
of a detonation. The residence time of a pressure pulse in the hot spot is r
0
/
ˆ
c = t
r0
,
and a dimensionless measure of this energy input into the pulse is
ε =
t
r0
τ
e
. (3.32)
Here ε is the number of excitation times feeding into the pressure pulse during its
residence in the hot spot.
In a detonation wave the coupling of the chemical reaction with the shock wave
results in a very damaging high-pressure spike, and this single entity propagates at
the detonation velocity. In addition to this mode of auto-ignitive propagation, there
are a variety of other modes, and these depend on the values of ξ and ε. They were
identified in DNSs of auto-ignitions at spherical hot spots. The simulations involved
detailed chemical kinetics over wide ranges of initial values of ∂T/∂r and r
0
[62, 63].
Equimole CO–H
2
mixtures with air at different φ were chosen for this study because
of their relatively simple detailed chemical kinetics.
172 Combustion Instabilities
ξ
ξ
ξ
ξ
ε
εε
ε
ξ
ξ
DEVELOPING
DETONATION
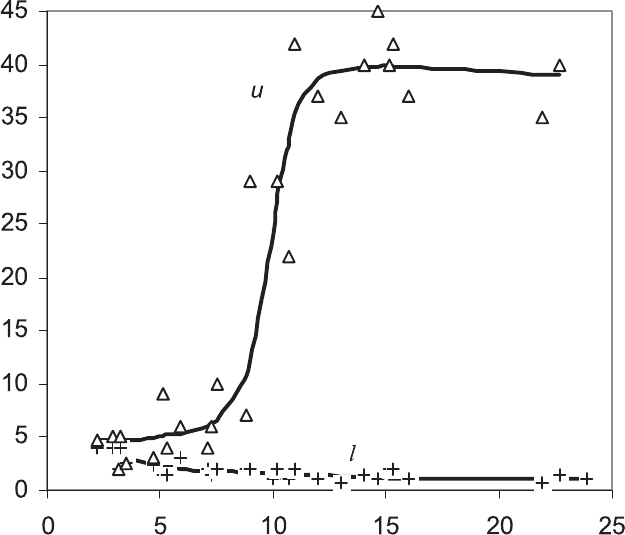
B
P
Figure 3.13. Developing detonation peninsula on plot of ξ against . Other modes are thermal
explosion below ξ
l
, supersonic and subsonic auto-ignitive fronts propagate in regions P and
B, respectively. From [62].
It was first necessary to compute values of τ
i
and τ
e
for different φ, p, and T .The
ensuing simulations ultimately identified the upper and lower limits of detonation,
ξ
u
and ξ
l
. These are indicated in Fig. 3.13,from[62], by the open triangle and
cross symbols. These define the boundaries of a developing detonation peninsula
within which detonations develop within a hot spot. Peak detonation pressures,
when normalised by the ambient pressure, increase with ε. Under these conditions
Eq. (3.30) cannot be used to predict the pressure pulse. At very low ε, as its value
increases, so does the range of ξ over which a detonation can develop at a hot spot.
At the highest values of ε this range does not appear to change. The smallest values
of ε are associated with the least-reactive lean mixtures and the largest values with
the most reactive, with φ = 1.0 and T = 1200 K.
With even more reactive mixtures, with values of ε of about 70, the detonation
can continue to propagate outside the hot spot in the absence of any gradient of
reactivity [64]. In addition, as the reactivity increases, so does the pressure ratio
at the detonation front and the hot-spot number density. Initially separate waves
from hot spots interact and are reinforced, inducing further auto-ignitions that can
generate severe engine knock [65]. Intersecting shock waves from closely packed
neighbouring hot spots can create enlarged (though not necessarily spherical) hot
spots that, because of their increased size and higher temperature and pressure,
have higher values of ε. Further study is needed to identify the initiating conditions,
