Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

3.2 Control Strategies for Combustion Instabilities 173

presumably with high values of ε and low values of ξ, under which a detonation can

propagate in the absence of a reactivity gradient [66].

Other modes of auto-ignition also are indicated in Fig. 3.13. These involve auto-

ignitive propagation in a supersonic mode below ξ

,withξ ≤ 1.0, in region P.From

Eq. (3.31), as

(

∂τ

/∂T

)

→ 0, u

→∞and ξ → 0. The reaction front moves so rapidly,

it runs ahead of the acoustic wave and Eq. (3.30) is again invalid. There is no sharp

pressure peak, as there is with a developing detonation, and the maximum pressure

tends towards that of constant-volume combustion. In the limit of ξ = 0athermal

explosion occurs instantaneously throughout the mixture, without any propagating

front. In region B,withξ>1.0 and also outside the peninsula, with ξ ≥ ξ

, auto-

ignitive propagation is subsonic and more benign.

An important practical aspect of this mode is that it can support combustion

in mixtures that are so lean that the turbulence would extinguish normal ﬂame

propagation. For non-stratiﬁed mixtures, the practical lean-burn limits for turbulent

ﬂame propagation in spark-ignition engines are about φ = 0.71 for gasoline–air [67]

and 0.62 for natural gas [68]. The addition of 60 vol% H

to CH

lowers this to

φ = 0.34 [69], whereas for H

–air the limit is about φ = 0.2, with effectively zero-NO

emission [70]. In sharp contrast, in the misnamed homogeneous charge-compression

ignition (HCCI) engine, auto-ignitive burning of gasoline–air mixtures is possible

down to φ = 0.25 and even lower, notwithstanding the increase in τ

as φ is reduced.

Controlled combustion is, in fact, dependent on a non-homogeneous charge,

in which gradients of reactivity drive auto-ignitive fronts. Multiple isolated auto-

ignitions are followed by combustion at distributed sites [71]. Chemiluminescent

imaging, with φ in the region of 0.24, showed sequential auto-ignition of progres-

sively cooler regions, with luminescence spreading through the charge with a prop-

agation speed of about 100 m s

−1

[72]. This is greater than that for normal turbulent

ﬂame propagation in spark-ignition engines. DNSs have shown that mixed types of

combustion are possible, in which auto-ignitive propagation coexists with laminar or

turbulent ﬂames [73].

Acknowledgement

To the late Arthur Smithells [1], in whose name a research studentship was awarded

to the author, enabling him subsequently to enjoy a lifetime in combustion research.

3.2 Control Strategies for Combustion Instabilities

By A. P. Dowling and A. S. Morgans

Lean premixed combustion systems are especially prone to thermoacoustic insta-

bilities, as noted in the discussion on RT instabilities in Subsection 3.1.1 and the

associated pressure oscillations and possibly enhanced heat transfer can lead to a

deterioration in the system performance and may even become sufﬁciently intense

as to cause structural damage. This means that control strategies are an important

element of the design of lean premixed combustors.

Combustion oscillations in conﬁned conﬁgurations usually arise because of cou-

pling between the unsteady heat release and the acoustic waves, and control strate-

gies need to interrupt this coupling. Passive control methods [74–76] may either

174 Combustion Instabilities

seek to reduce the susceptibility of the combustion process to acoustic excitation

through ad hoc hardware design changes, s uch as modifying the fuel injection system

or combustor geometry [77–79], or to remove energy from the sound waves by using

acoustic dampers such as Helmholtz resonators [80–82], quarter-wave tubes [83],

perforated plates, or acoustic liners [84, 85]. The problem with passive approaches is

that they tend to be effective over only a limited range of operating conditions. Also

they may be ineffective at the low frequencies at which some of the most damaging

instabilities occur and the changes of design involved are usually costly and time

consuming. The range of operation of a passive device can be extended by introduc-

ing an element of variable geometry, a variable volume in a Helmholtz resonator for

example, and altering the geometry to retune the device as the instability frequency

changes with changes in operating condition.

Active feedback control provides another means of interrupting the coupling

between acoustic waves and unsteady heat release. An actuator modiﬁes some system

parameter in response to a measured signal. The aim is to design the controller (the

relationship between the measured signal and the signal used to drive the actuator)

such that the unsteady heat release and acoustic waves interact differently, leading

to decaying, rather than growing, oscillations. In the past, approaches to controller

design were somewhat empirical, but more systematic approaches such as robust

control and adaptive control are now promoted.

In Subsection 3.2.1 the physics of these combustion oscillations is discussed and

a generalised energy equation is derived to identify what is needed for control.

Passive control techniques are described in Subsection 3.2.2, including factors that

affect their practical implementation in combustion systems. Techniques for tuning

passive devices are introduced in Subsection 3.2.3, and active control is discussed in

Subsection 3.2.4.

3.2.1 Energy and Combustion Oscillations

Self-excited combustion oscillations occur because of interactions between unsteady

combustion and acoustic waves. Rayleigh’s criterion [ 29, 30], noted in Subsec-

tion 3.1.1, states that an acoustic wave gains energy when heat is added in phase

with pressure, but loses energy when heat is added out of phase with pressure. This

clearly explains the energy exchange between acoustic waves and heat release, which

forms the basis for the majority of combustion oscillations. Chu [86] has since gen-

eralised this to incorporate the effect of boundary conditions, and this provides a

useful insight into combustion oscillations and methods for controlling them.

Following Chu [86], let us consider a perfect gas burning within a combustor of

volume V , bounded by the surface S, as illustrated in Fig. 3.14. For simplicity in this

illustrative example, the gas is considered linearly disturbed from rest with no mean

heat release (extensions accounting for mean ﬂow and mean heat release can be

made [87]). Viscous forces are neglected. The pressure, density, heat release rate per

unit volume, particle velocity, speed of sound, and ratio of speciﬁc heat capacities

are denoted by p, ρ, q, u,

c, and γ, respectively, and a mean value is indicated by an

overbar and a ﬂuctuating value by a prime.

We consider the inﬂuence of unsteady heat q

(

x, t

)

on pressure perturbations.

The density ρ varies through changes in both the pressure p and speciﬁc entropy s.

3.2 Control Strategies for Combustion Instabilities 175

Figure 3.14. Combustion within a resonator.

The chain rule of differentiation shows that

Dρ

∂ρ

∂s



. (3.33)

When viscous and heat conduction effects are neglected, ρT Ds/Dt = q(x, t),

where T is the absolute temperature. Moreover, for a perfect gas, ∂ρ/∂s

=−ρ/c

−ρT

(

γ − 1

)

, where c

is the speciﬁc heat at constant pressure. Substitution into

Eq. (3.33) leads to

Dρ



−

(

γ − 1

)



. (3.34)

Equation (3.34) may be applied to a combusting gas, provided that the reactants

and products behave as perfect gases, and there is no molecular weight change during

the chemical reaction [88]. After linearisation it becomes

Dρ



∂p



∂t

−

(

γ − 1

)



. (3.35)

The ﬁrst term on the right-hand side describes the change in density that is

due to compressibility, and the second term accounts for the combustion effects.

Substitution from Eq. (3.35) into the equation of mass conservation leads to

∂p



∂t

∂u

∂x

(

γ − 1

)

q, (3.36)

where q = q



and u = u



in the present approximation. Multiplying Eq. (3.36)byp



and adding it to the scalar product of the linearised momentum and the velocity

vector u leads to

∂

∂t



ρu





∂(p



)

∂x

(

γ − 1

)



q. (3.37)

176 Combustion Instabilities

Finally, after integration over the volume V , this yields

∂

∂ t





ρu





dV =



(γ − 1)



qdV −





u · dS. (3.38)

The term on the left-hand side of Eq. (3.38) represents the rate of change of

the sum of the kinetic and potential energies within the volume V . The ﬁrst term on

the right-hand side describes the exchange of energy between the combustion and

acoustic waves; as noted by Rayleigh, when the pressure and the rate of heat release

have a component that is in phase (i.e., when the phase difference lies between −90

◦

and +90

◦

), the acoustic energy tends to increase. The ﬁnal surface term accounts for

energy loss across the bounding surface S, which occurs because the ﬂuid within S

does work on its surroundings. Viscous dissipation has been neglected.

Equation (3.38) states that disturbances grow if their net energy gain from the

combustion is greater than their energy losses across the boundary. Therefore an

acoustic mode grows in amplitude if



(

γ − 1

)

ρ ˆ



q dV >





u · dS, (3.39)

where the overbar denotes an average over one period of the acoustic oscillation.

This is a generalised form of Rayleigh’s criterion. When it is satisﬁed, the combustor

has a thermoacoustic instability. Linear waves increase in amplitude until limited by

nonlinear effects. If the nonlinearity appears primarily in the heat release rate with

the acoustic waves remaining linear, it is clear that, for a system in which acoustic

waves are initially growing, heat release saturation or phase-change effects may cause

the terms to become equal at a certain pressure amplitude. This is the amplitude at

which limit cycle oscillations occur [89–91].

In combustors there have traditionally been a large number of inlet ports, both

primary and secondary, together with many cooling holes and rings. Across each of

these, there is a pressure drop, and the perturbations in pressure and velocity tend to

be in phase, resulting in damping according to the last term in Eq. (3.38). However,

to achieve lean burn, most of the airﬂow is routed through the premixing ducts,

leaving little air available for cooling. This means that there is little natural acoustic

damping in the combustor. Moreover, in lean premixed combustion systems, the

ﬂame responds signiﬁcantly (i.e., q



is nonzero) across a broad range of frequencies

[77]. We might therefore expect such combustors to be particularly susceptible to

combustion instability.

As well as offering insight into the energy transfers that give rise to and limit the

size of combustion oscillations, relation (3.39) also suggests ways in which combustion

instabilities can be eliminated. Either the energy source term,





q dV ,mustbe

decreased or the surface loss term,





u·dS, must be increased. Passive and active

control methods can target either term.

3.2.2 Passive Control

MODIFYING THE FLAME RESPONSE. One means of passive control is to seek to modify

the fuel input or the ﬂame shape to reduce the energy source term on the left-hand

3.2 Control Strategies for Combustion Instabilities 177

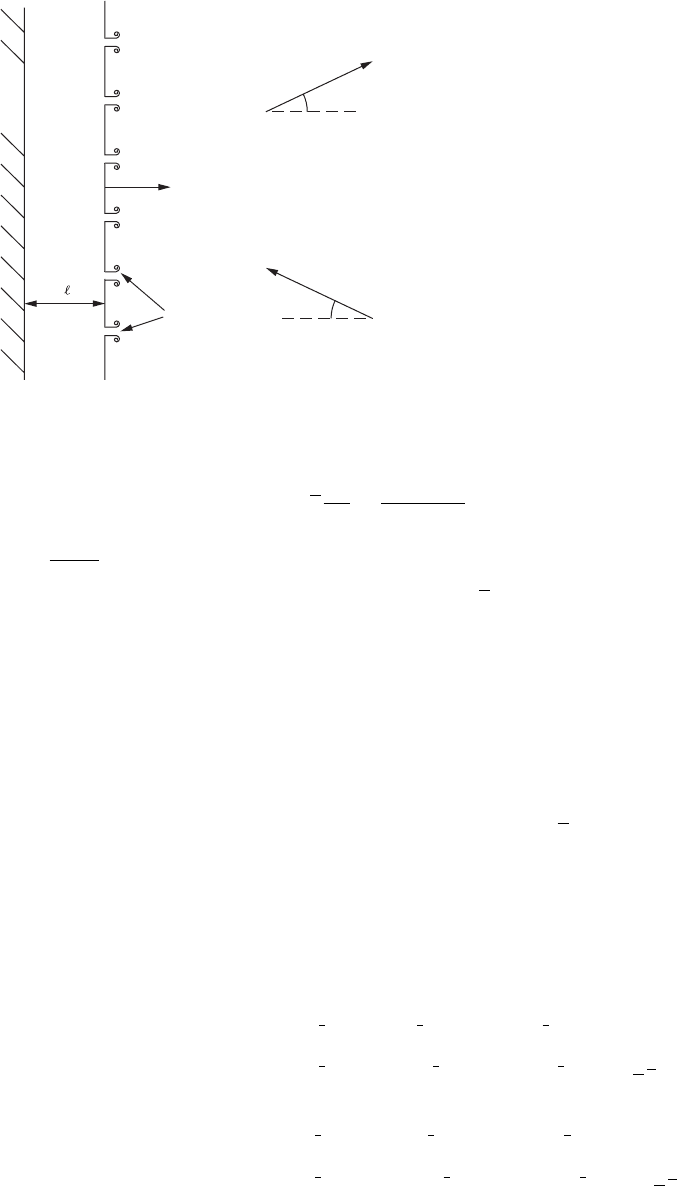
Figure 3.15. Fuel–air ratio ﬂuctuations from fuel bars πu

/ω apart cancel in the combustor.

side of relation (3.39) [4, 5]. Design changes might, for example, choose to alter

the position of the ﬂame or of the fuelling system to change the phase relation-

ship between oscillations in combustor pressure and the rate of heat release so

that





q dV < 0, (3.40)

ensuring that the interaction between the acoustics and the combustion tends to

dampen the pressure oscillations. But there are more subtle ways of changing this

driving term. For example, for a plane-wave instability, one might choose to introduce

some asymmetry into q(x,t): Then there is some cancellation in the integral of



over the combustor cross section. Such asymmetry could be introduced by ensuring

an angular variation in fuel distribution or in ﬂame position.

Convection time delays from fuel input to combustion are important in deter-

mining the ﬂame transfer function (FTF), and this can be exploited to reduce the

ﬂame response to ﬂow unsteadiness. Staging the fuel injection locations axially within

the premixing ducts, so that the fuel–air mixture from different fuelling bars reaches

the combustor after different time delays, can reduce the susceptibility to combustion

instability [78]. The situation is illustrated in Fig. 3.15. If the two fuel injection bars

are close compared with the acoustic wavelength, they both experience the same air

velocity and pressure perturbation and so instantaneously produce the same ﬂuctu-

ation in fuel–air ratio. If their axial separation corresponds to half the convection

wavelength (i.e., is equal to π

/ω, where u

is the mean convection velocity and ω

is the radian frequency of the ﬂow perturbations), these fuel–air ratio ﬂuctuations

arrive at the combustion zone half a period apart, thereby reducing perturbations in

fuel–air ratio and hence in the related ﬂuctuations in the rate of heat release. Nearly

complete cancellation is possible for a single frequency of oscillation. By the axial

distribution of many injection points, reductions in the ﬂame transfer function and

hence in the susceptibility to oscillation can be achieved across a wide frequency

range [92].

178 Combustion Instabilities

iωt

m′(t)

Figure 3.16. Sound incident upon an oriﬁce.

SOUND ABSORPTION. Passive acoustic dampers aim to increase the energy loss on

reﬂection at the combustor boundaries, typically by converting energy in the acoustic

wave into vorticity. If there is a hole in the bounding surface of the combustor such

that when p



is high u is outward, according to relation (3.39), this tends to dampen

the oscillation.

PERFORATED PLATES. Perforated plates exploit this mechanism, which can be en-

hanced if the hole is at the entrance to an acoustic resonator causing small pressure

perturbations to induce large velocity ﬂuctuations. This is usually done by attaching

a resonator, for example a Helmholtz resonator [7, 8] or quarter-wave tube [83],

to the walls of the combustor or by inserting perforated plates [85]. When used in

combustors, the neck of a Helmholtz resonator or the holes of a perforate need to be

cooled by blowing cooler air through them. The interaction between acoustic waves

and the oriﬁce leads to unsteady vortex shedding, which is convected away by the

mean ﬂow. If the Strouhal number of the ﬂow in the oriﬁce is chosen appropriately,

this can be used to enhance the absorption of acoustic energy [93–95].

Howe [93] considered a sound wave that causes an incident pressure pertur-

bation p

iωt

at a circular aperture in a rigid plate [as usual, the actual pressure

perturbation is the real part of the complex amplitude p



(t) =

iω t

]. This leads

to a ﬂuctuating mass ﬂux m



(t) through the aperture (see Fig. 3.16). Howe determines

K such that



= Kp

iωt

. (3.41)

In the absence of a mean ﬂow, K = 2a, where a is the radius of the aperture.

With a mean ﬂow through the aperture, K = 2a(η + iδ), where η and δ are functions

of the Strouhal number ωa/

u. Howe determined the functional forms of η(ωa/u)

and δ(ωa/

u) in terms of Bessel functions, and these are plotted in Fig. 3.17.

The sound transmitted and reﬂected by a perforated plate can be determined

by combining the results for individual holes [93]. Consider the plate illustrated

3.2 Control Strategies for Combustion Instabilities 179

/2a

0.8

0.4

Strouhal number ωa/ u

Figure 3.17. The dependence of the aperture con-

ductivity K = 2a(η + iδ) on the Strouhal number

ωa/

u [93].

in Fig. 3.18, with holes of radius a separated by distance d. There are hence d

−2

apertures/area. The plate is illuminated with sound of frequency ω, resulting in

reﬂected and transmitted waves. Provided d is small in comparison with

c/ω,we

can work with smoothed ﬂow variables averaged over many holes. The smoothed

velocity normal to the plate, u



(x, t), is related to the mass ﬂow rate through an oriﬁce

ρu



= m



Continuity of mass across the plate shows that the area-averaged velocities



(x, t) are the same on the two sides of the plate, i.e.,

[



]

x=0

−

x=0

= 0. (3.42)

From Eq. (3.41),

∂m



∂t

= K

[



]

x=0

−

x=0

= 2a(η + iδ)p



, (3.43)

Figure 3.18. Geometry of a perforated

plate.

180 Combustion Instabilities

Reflected sound

Incident soun

Aperture

wakes

Rigid

plane

Figure 3.19. Sound incident at angle θ on a

perforated plate at x = 0 with a rigid backing

plate a distance  behind it.

where p



[



]

x=0

−

x=0

, the difference in the smoothed pressure ﬂuctuation p



(x, t)

across the plate, and K = 2a(η + iδ). Rewriting Eq. (3.43) in terms of u



gives

∂u



∂t

2a(η + iδ)

p



. (3.44)

We see that it is δ, the imaginary part of K, that gives an non-zero value to



p



that describes the rate of absorption of acoustic energy/unit plate area. In the

absence of a mean ﬂow, the Strouhal number ωa/

u tends to inﬁnity, δ tends to zero

(see Fig. 3.17), and there is no sound absorption by the linear elements of the pressure

perturbation. Then it is only the elements of p



of the order of u

n

, where n ≥ 2, that

give the sound absorption. Absorption by this mechanism is discussed further in

Subsection 3.2.3. It is effective only for large-amplitude sound waves. Ideally we

would like good absorption at low amplitudes so that the pressure perturbations in a

combustion oscillation could be controlled to be at a low level. This is possible when

there is a bias or mean ﬂow through the apertures. Then the fraction of incident

sound energy absorbed is independent of amplitude but relies on a nonzero value of

δ. We see from Fig. 3.17 that the maximum δ occurs for ωa/

u ≈ 1.

When perforated plates are used in combustors they are usually as wall liners.

Hughes and Dowling [84] used Howe’s results to determine the sound absorbed in

an incident plane wave by a perforated liner has a rigid backing plate a distance 

behind it, as illustrated in Fig. 3.19, after neglecting the axial evolution of pressure

wave.

If I and R denote the pressure amplitude of the incident and reﬂected waves in

x = 0,



(x, t) = e

iω(t−y sin θ/

(Ie

iωx cos θ/

−iωx cos θ/



(x, t) = e

iω(t−y sin θ/ˆ

(−Ie

iωx cos θ/ˆ

−iωx cos θ/ˆ

) cos θ/(ρ ˆ

c). (3.45)

While in − ≤ x ≤ 0, the rigid-wall condition u



= 0onx =− gives



(x, t) = Ae

iω(t−y sin θ/

iω(x+)cosθ/

+ e

−iω(x+)cosθ/

]



(x, t) = Ae

iω(t−y sin θ/

[−e

iω(x+)cosθ/

+ e

−iω(x+)cosθ/

] cos θ/(ρ

c), (3.46)

where A is a complex constant.

3.2 Control Strategies for Combustion Instabilities 181

Resonance parameter, Q

(a) (b)

1.0

Absorption coefficient, Δ

2.0

1.0 2.0

Figure 3.20. The variation of the absorption coefﬁcient  with Q for (a) M = 0.014, a/ =

0.15, and a/d

= 0.052, and (b) M = 0.052, a/ = 0.032, and a/d

= 1.06 (from [11]).

The reﬂected-wave amplitude R can be found in terms of the incident-wave

amplitude I after substitution from Eqs. (3.45) and (3.46)into(3.42) and (3.44). The

fraction of the incident energy absorbed  then follows from

 = 1 −

. (3.47)

The backing screen introduces an additional non-dimensional parameter /a

into the problem. Hughes and Dowling [84] found it convenient to use a ‘resonance’

parameter, Q = ω

/ω

, where ω

= ˆ

c[2a/(cos θd

)]

1/2

. The absorption coefﬁcient

is then a function of three non-dimensional parameters, Q, ω cos θ/

c, and ωa/

The variation of absorption coefﬁcient with Q for ﬁxed Mach number M =

u/ˆ

c and

two different plate geometries is shown in Fig. 3.20. The predictions are compared

with experimental results for a normally incident sound wave. There is excellent

agreement between predictions and experiment.

Hughes and Dowling [84] went on to develop design rules: Typically the peak

sound absorption is near Q = 1 (the exceptions to this are when the gap is non-

compact or the mean velocity is very high). Then Fig. 3.21 can be used to choose

an appropriate Strouhal number. It is evident from Fig. 3.21 that very high levels of

absorption can be achieved if plate parameters are chosen appropriately.

1.0

0.5

0.1

0.3

0.5

= 0.05

Absorption coefficient, Δ

024

Strouhal number, ωa /u

6810

ω cos c

Figure 3.21. Absorption coefﬁcient for

a plane-backed perforated screen when

Q = 1. (from [11]).

182 Combustion Instabilities

iω(t − x/c )

Figure 3.22. Lined section of duct of length L.

However, this theory gives no absorption when the incident wave is tangential

to the plane of the liner (θ =±90

). Then, although Eq. (3.41) is still appropriate

to describe an individual aperture, the axial evolution of the waves needs to be

considered.

Eldredge and Dowling [85] considered the geometry shown in Fig. 3.22. They

used the perforated-plate impedance Eq. (3.44) to determine the axial evolution

of ∂p



/∂x over the lined section. They then went on to determine the absorption

of an incident plane wave Ie

iω(t−x/ˆ

and to develop design criteria to optimise the

absorption.

Figure 3.23(a) shows that over 80% of the incoming sound energy can be ab-

sorbed by a perforated lining plate, provided the plate parameters are chosen ap-

propriately. An inappropriate choice for parameters leads to little absorption [see

Fig. 3.23(b)]. For optimal absorption the perforated plate should be located in the

duct near a pressure antinode, and M

, the Mach number of the ﬂow through the

holes, should be chosen to be near σ CL/(A

√

2), where σ is the open-area ratio, C is

the circumference of the lined duct, L is its length, and A

denotes its cross-sectional

area.

HELMHOLTZ RESONATORS. A Helmholtz resonator is another passive damping de-

vice. Figure 3.24 shows an idealised system consisting of a Hemholtz resonator con-

nected to the side of a duct. A Helmholtz resonator consists of a standard acoustic

device with a short neck opening out into a large volume [96, 97]. The absorption ob-

tained from a Helmholtz resonator can also be enhanced by cooling ﬂows through its

neck [82, 98]. Again the location of the Helmholtz resonator(s) within the combustor

has a major inﬂuence on its effectiveness. The absorption of sound by a Helmholtz

resonator can be analysed in a straightforward way.

1.0

0.8

0.6

0.4

0.2

Fraction of incident

energy absorbed

0 0.02

(a)

0.04 0.06

1.0

0.8

0.6

0.4

0.2

0 0.02

(b)

0.04 0.06

Figure 3.23. Fraction of incident sound energy absorbed by a perforated plate of length L:

(a) ωL/

c = 0.89, (b) ωL/

c = 1.22, M

is the Mach number of the mean ﬂow through the holes

(from [85]).