Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

3.2 Control Strategies for Combustion Instabilities 193

controller

filter

microphone

loudspeaker

flame stabilised

on grid

white noise

controller

K(s)

Rijke tube

loudspeaker

open-loop system, G(s)

microphone

+ filter

−

loudspeaker

input to

microphone/filter

output from

ref

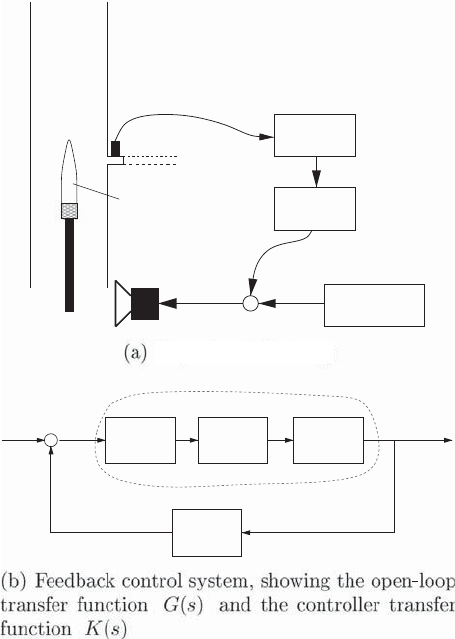
Experimental setup

Figure 3.30. The Rijke tube exhibiting

a combustion instability.

MEASURING THE OPEN-LOOP TRANSFER FUNCTION (OLTF). The transfer function ap-

proach to controller design, also known as classical control theory, is used in con-

troller design. For an overview of this refer to [135, 136]

The OLTF needed for control purposes is from the actuator signal to the sensor

signal, in this case from t he loudspeaker voltage V

to the ﬁltered microphone reading

ref

. This is shown as G(s)inFig.3.30(b), where s denotes the Laplace transform

variable. As with all naturally unstable systems, characterising G(s) is complicated by

the fact that, during instability, nonlinear limit cycle behaviour dominates and masks

the linear relationship that would be observed at low oscillation amplitudes. To

prevent the growth of small perturbations, it is measurement of the linear behaviour

that is required for controller design.

To overcome this problem, a loudspeaker voltage input V

is used, which com-

prises two components:

1. a control signal from a trial-and-error controller to eliminate the nonlinear limit

cycle, and

2. a wide bandwidth signal, in this case white-noise signal from a white-noise

generator, for identiﬁcation of the OLTF.

One may ask this question: If a trial-and-error controller has been found, why do

we need to design another controller? The answer lies in the superior performance

194 Combustion Instabilities

2000 4000 6000 8000 10000

−50

−40

−30

−20

−10

Gain in dB

2000 4000 6000 8000 10000

−720

−360

−540

−180

Phase in deg

ω in rad/s

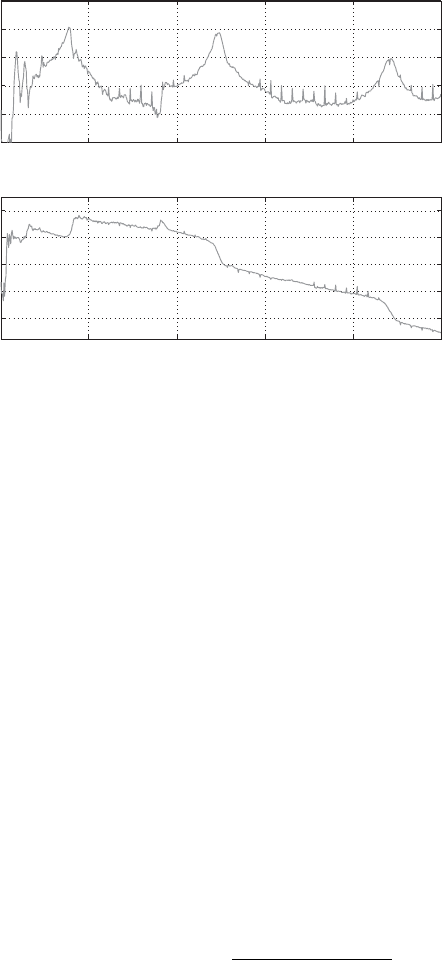
Figure 3.31. The measured Bode diagram of G(s) = p

ref

(s)/V

(s) for the Rijke tube.

of a model-based controller: Feedback control is most successful when an accurate

model of the system to be controlled is available.

Measuring the OLTF involves applying the preceding voltage input to the loud-

speaker, recording the r esponse of the ﬁltered microphone signal, and using the

ratio of Fourier transforms to deduce the open-loop frequency response G(iω). Note

that it is important to use the total loudspeaker voltage in deducing this, not just

the white-noise component. Although the controller causes the loudspeaker input

spectrum to have a peak at the unstable frequency, applying sufﬁciently loud white

noise ensures that this peak does not dominate.

The open-loop frequency response G(iω) is shown as the Bode diagram of G(s)

in Fig. 3.31. The magnitude peaks represent system resonances and correspond to

the various ‘organ-pipe’ modes of the acoustic waves in an open-ended tube. For

example, the fundamental frequency of an open–open tube has a wavelength of

twice the tube length, in this case 1.5 m. The fundamental frequency is then c/(2L),

where

c is the speed of sound in the tube. Taking this to be 360 m/s gives a fundamental

frequency of 240 Hz or approximately 1500 rad/s, which is the frequency of the ﬁrst

modal peak.

By considering each modal peak to be caused by a second-order transfer func-

tion,

+ 2ζ

s + ω

)

stability information can be deduced from the phase change across the modal peaks.

A phase increase of 180

◦

indicates an unstable conjugate pair of poles (ζ

< 0)

whereas a phase decrease of 180

◦

indicates a stable conjugate pair (ζ

> 0). The

measured transfer function shows that the ﬁrst (fundamental) mode is unstable,

whereas all other modes are stable.

CONTROLLER DESIGN. The system is single-input–single-output, and so Nyquist tech-

niques [135, 136] provide a suitable means of designing robust controllers. The exper-

imentally characterised G(iω) can then be used directly in controller design: Subject

3.2 Control Strategies for Combustion Instabilities 195

−0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3

−0.25

−0.2

−0.15

−0.1

−0.05

0.05

0.1

0.15

0.2

0.25

Real part

Imaginary part

(a) G (iω)

−2 −1.5 −1 −0.5 0 0.5 1

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Real part

Imaginary part

−1

(b) G(iω)K(iω)

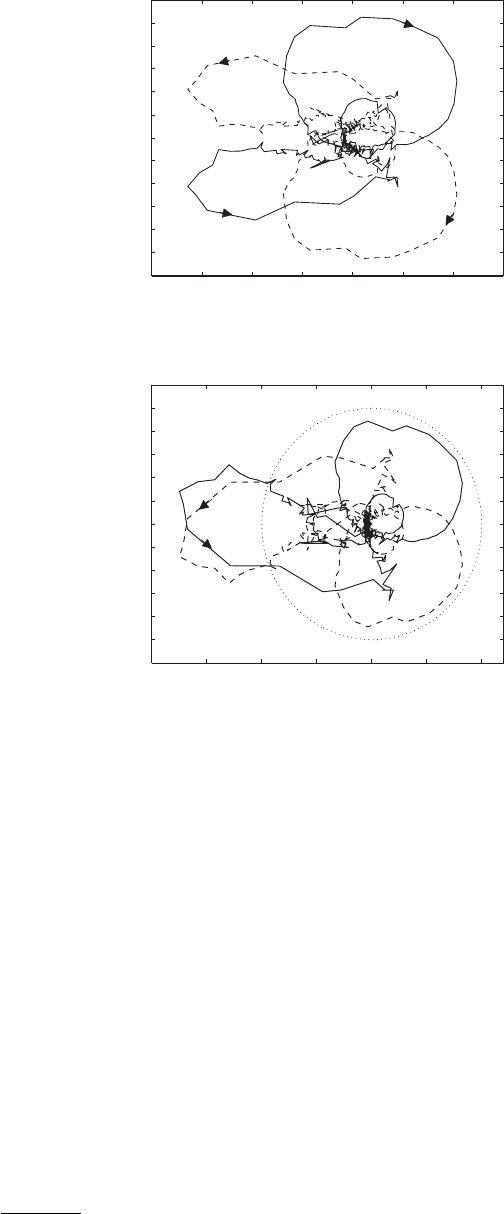
Figure 3.32. Nyquist diagrams: positive ω,---

negative ω.

to the system having low noise, there is no need to model or approximate what has

been measured. The Nyquist diagram for G(s)isshowninFig.3.32(a). According to

the Nyquist criterion, a negative feedback system such as that in Fig. 3.30 is stable if

the number of anticlockwise encirclements of the −1 point shown by the controlled

OLTF, G(s)K(s), is equal to the number of unstable poles in the uncontrolled OLTF,

G(s)[135, 136]. The phase increase across the ﬁrst mode conﬁrms that this is the

only unstable mode and that it has a pair of unstable poles associated with it. The

Nyquist plot for G(s)K(s) therefore needs to encircle the −1 point in an anticlock-

wise direction twice in order for the closed-loop system to be stable. The Nyquist

plot for G(s) has no encirclements of the −1 point. To achieve two encirclements, it

is clear that the controller should introduce both gain and additional phase lag near

the frequency of the unstable mode.

A good choice of controller structure to achieve this is that of a phase-lag

compensator:

K(s) =

k(s + βa)

(s + a)

, where β ≥ 1. (3.61)

196 Combustion Instabilities

The maximum lag should be close to the location of the unstable mode, which from

the Bode plot in Fig. 3.31 is at a frequency of ω = 1600 rad/s. The maximum lag of

the phase-lag compensator in Eq. (3.61) occurs at an approximate frequency of a

√

β,

and so good choices of values for the controller are a = 980, β = 2.67. These values

give a good compromise between maximising the phase and gain margins. The value

of k is then chosen to be 3.1 to maximise the gain margin (note that the gain–phase

margins must be considered in terms of both reducing and increasing the gain or

phase because two encirclements of the −1 point are required).

The resulting Nyquist plot for G(s)K(s) is shown in Fig. 3.32(b). It can be seen

that there are indeed two anticlockwise encirclements of the −1 point. The gain

margin is 4.5 dB and the phase margin is 21

◦

; thus the closed-loop system should

be stable and reasonably robust to plant uncertainties and changes (if needed, the

stability margins could be increased by use of a higher-order controller).

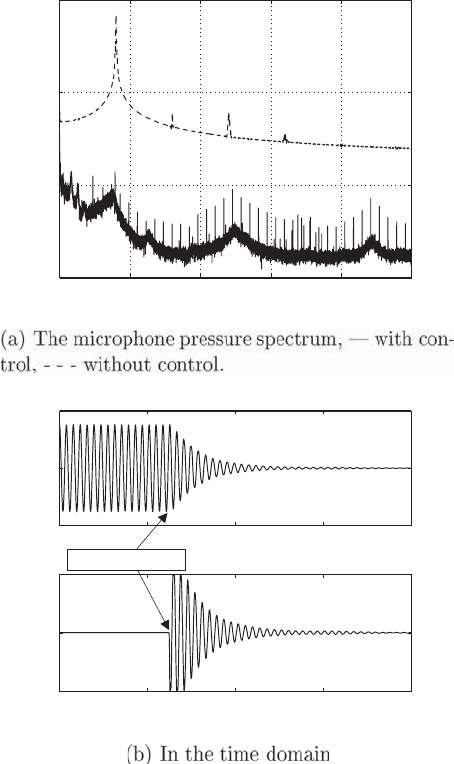
CONTROLLER IMPLEMENTATION. After the preceding controller is implemented on

the Rijke tube, it is seen to eliminate the combustion instability. The effects of

control on both the measured pressure spectrum and the time-domain oscillations are

shown Fig. 3.33. Control gives a reduction of approximately 80 dB in the microphone

pressure spectrum: This represents a reduction of four orders of magnitude. The

controller obtains control rapidly, with oscillation amplitudes down to 10% of their

unstable levels in fewer than 10 oscillations. Although the loudspeaker voltage is

initially large in order to attain control, once control has been achieved very little

actuator effort is needed to maintain it.

CONTROL STRATEGIES – ADAPTIVE CONTROL. The type of model-based controllers

considered so far are robust to small changes, but are essentially designed for a

single operating condition. Their redesign would be necessary should the operating

conditions change signiﬁcantly. Adaptive controllers, whose parameters are contin-

ually updated to track plant changes, offer an efﬁcient means of achieving control

across a range of operating conditions. Although some adaptive controllers, such

as neural networks, gain information about the plant ofﬂine [137, 138], others treat

the combustion system as a ‘black box’ and rely on an online system identiﬁca-

tion. The ﬁrst adaptive controllers to be applied to combustion oscillations were

least-mean-squares (LMS) controllers [139, 140]. These have the form of inﬁnite-

impulse-response (IIR) ﬁlters whose coefﬁcients are updated according to the LMS

algorithm [141]. Despite recent improvements to the online system identiﬁcation

within the algorithm [142], LMS controllers are unlikely to be sufﬁciently robust for

use in practical applications as they rely on assumptions such as the primary noise

source being slowly varying and do not offer any guarantees of global stability.

Possibly the most physics-based type of adaptive control is guided directly by

the Rayleigh criterion [105, 143]. Open-loop testing is ﬁrst used to determine the

time delay between the actuator input signal and the heat release rate as a function

of frequency. When control is activated, a real-time observer, similar to the one

described in Subsection 3.2.3, is used to detect and track the frequencies, amplitudes,

and phases of several combustor modes. This real-time detection combined with the

open-loop information then allows fuel to be added unsteadily such that the heat

release rate is exactly out of phase with the pressure ﬂuctuations. Even though only

3.2 Control Strategies for Combustion Instabilities 197

0 2000 4000 6000 8000 10000

100

150

Sound pressure level in dB

Frequency in rad/s

4.3 4.35 4.4 4.45 4.5

−500

500

time in s

mic pressure in Pa

4.3 4.35 4.4 4.45 4.5

−5

time in s

loudspeaker voltage in V

control switched on

Figure 3.33. The effect of the model-

based controller on the Rijke tube

instability.

a gain–time-delay controller is used, the observer ensures that any secondary peaks

created are detected so that the control action can adapt to the new frequencies. This

approach has been demonstrated experimentally on a large-amplitude instability in

a small-scale gas rocket motor, in which the observer detected the most dominant

mode, and has since been extended to a full-scale gas turbine combustor [144].

A particularly attractive approach to adaptive control, which avoids the need

for either detailed prior measurements or online system identiﬁcation, is to use self-

tuning regulators (STRs). The remainder of this subsection discusses the use of STRs

as adaptive controllers.

STR ADAPTIVE CONTROL THEORY. STRs are model-based adaptive controllers [145].

They use some general properties of the open-loop system to infer the controller

structure needed for stability and then update the controller parameters by using

a Lyapunov-based algorithm. A brief outline of STR background theory is now

provided.

198 Combustion Instabilities

For the class of combustion systems whose OLTF has relative degree

∗

equal

to 1 or 0, it follows from root-locus arguments that a ﬁrst-order compensator of the

form

K(s) = k

s + z

s + p

(3.62)

can always stabilise the system if its parameters are chosen correctly. The adaptive

control algorithm seeks to ﬁnd stabilising values for the parameters of this ﬁrst-order

compensator. Note that real combustion systems have inﬁnite dimension because of

the presence of time delays. In practice, the requirement that n

∗

= 0 or 1 therefore

translates to the requirement that the OLTF is well approximated by a rational

transfer function with n

∗

= 0 or 1 over a sufﬁciently wide frequency range.

If we deﬁne W

∗

(s) as the transfer function of the resulting closed-loop stabilised

system, the derivation of such an adaptive control algorithm relies on W

∗

(s) being

strictly positive real (SPR). If W

∗

(s) is SPR, it is possible to form a positive-deﬁnite

Lyapunov function which depends on the s tates (in a state-space sense) of W

∗

(s)

and a control vector k. Because the Lyapunov function is positive-deﬁnite, it can

be thought of as an energy function. The time derivative of the Lyapunov function

is guaranteed to be negative if the time derivative of the control vector k obeys a

certain rule: This provides the updating rule for the controller parameters. When this

updating rule is used, the Lyapunov function is guaranteed to decrease monotonically

in time and the control vector k is guaranteed to converge to a stabilising value (which

we call k

∗

). The existence of such a Lyapunov function – which depends on W

∗

(s)

being SPR – is crucial for obtaining an adaptation algorithm that guarantees stability.

∗

(s) being SPR requires that

∗

(s) has no right half-plane (RHP) zeros (i.e., the closed-loop system is mini-

mum phase),

the high-frequency gain of W

∗

(s) is positive, and

[W

∗

(s)] > 0 for all s, which is equivalent to the phase of W

∗

(s) lying in the

range −π/2toπ/2.

For a more rigorous deﬁnition of SPR transfer function, see Narendra and

Annaswamy [145]. We now look at how each of these three requirements relates to

the properties of combustion systems.

Attention is restricted to longitudinal combustion systems governed by 1D

acoustic behaviour. For these, active control is typically achieved by fuel actua-

tion at a single location and pressure sensing at a single location. The OLTF needed

for control purposes is from the actuator signal V

to the sensor pressure p

ref

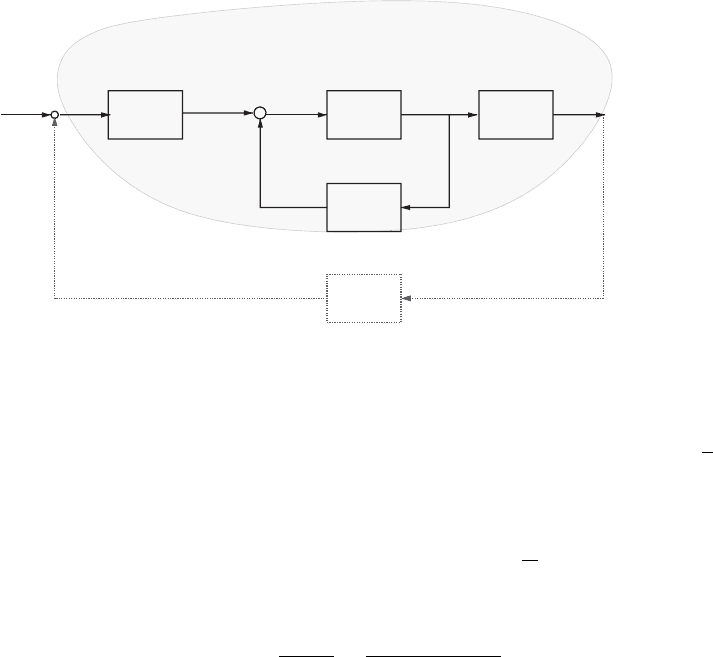
general model describing the constituent physical processes is shown in Fig. 3.34.It

includes the effect of the actuator, the ﬂame, and the acoustics.

Physically, changes in the actuator voltage V

result in fuel mass-ﬂow-rate ﬂuctu-

ations m



. These and the air mass-ﬂow-rate ﬂuctuations at the combustion zone, m



combine to change the equivalence ratio according to φ



/φ = m



− m



.Itis

generally agreed that ﬂuctuations in the heat release rate respond to both ﬂuctuations

in the equivalence ratio and in the air mass ﬂow rate [146, 147]. Recent experimental

The relative degree of a transfer function n

∗

is deﬁned as the degree of the denominator minus the

degree of the numerator.

3.2 Control Strategies for Combustion Instabilities 199

m (s)

ref

p (s)

acoustics

flame

H(s)

Q(s)

φ(s)

V (s)

c W (s)

actuator acoustics

F(s)

m (s)

heat

release

air flow

at premix

controller

fuel flow rate

valve

voltage

equiv. rato

pressure

measured

K(s)

A(s)

UNSTABLE OPEN-LOOP SYSTEM G(s)

Figure 3.34. Block diagram for a general longitudinal combustion system.

work suggested that, when the ﬂame is compact, heat release ﬂuctuations are domi-

nated by the response to equivalence ratio changes [148]. Assuming a compact ﬂame,

the heat release ﬂuctuation Q



is modelled by the relationship Q(s) = H(s)φ(s)/φ,

where H(s) is the ﬂame model and s = iω is the Laplace transform variable.

The response of the pressure measurement, p

ref

, to the heat release ﬂuctuation,



, is modelled by an acoustic transfer function F (s), and the response of the frac-

tional air mass ﬂow ﬂuctuation at the combustion zone, m



, to the heat release

ﬂuctuation Q



is modelled by A(s). The overall OLTF G(s) can then be expressed as

G(s) =

ref

(s)

(s)H(s)F (s)

1 + A(s)H(s)

. (3.63)

Using this general model, we can interpret the three requirements for W

∗

(s)to

be SPR as follows:

1. W

∗

(s) has no RHP zeros: The zeros of the open-loop plant G(s) become the

zeros of W

∗

(s). G(s) has no RHP zeros if the actuator transfer function W

(s),

the FTF H(s), and the acoustic transfer function F (s) are all free of RHP zeros.

It can be shown that the latter condition requires that the acoustic reﬂection

coefﬁcients at all combustor boundaries have magnitudes less than unity and

that the temperature ﬂuctuations generated by unsteady combustion are largely

dissipated before reaching the end of the combustor [149].

2. The high-frequency gain of W

∗

(s) is positive: This requires that the sign of the

high-frequency gain g

of the open-loop system is also positive, sgn(g

) > 0.

As long as the sign of g

is known, however, the algorithm can be modiﬁed to

guarantee stability.

3. [W

∗

(s)] > 0 for all s: This corresponds to the phase of W

∗

(s) lying between

−π/2 and π/2. Meeting this requirement means that the OLTF must have a

relative degree n

∗

of 0 or 1 [because n

∗

) = n

∗

(G)]. The phase change caused

by any time delay must also be negligible. Furthermore, the zeros and poles must

be ‘close’ in some sense; for example in systems dominated by second-order poles

and zeros, the pole and zero pairs would need to interlace.

200 Combustion Instabilities

For a combustion system whose OLTF obeys the preceding properties, the phase

compensator of Eq. (3.62) is implemented in the form

K(s) = k

(t)

s + z

+ k

(t)

, (3.64)

where z

is prescribed and k

(t) and k

(t) are the adaptive parameters that we seek

to tune to stabilising values. We deﬁne a control vector k(t) = [k

(t) k

(t)]

and a

data vector d(t) = [p

ref

(t)

(s+z

)

]

. The control signal sent to the actuator, V

(t), can

then be written as the dot product of k(t) and d(t), i.e., V

(t) = k(t) · d(t).

It can be shown that if we update the values of the control vector according to

the rule

k(t) = p

ref

(t)d(t), (3.65)

then the elements k

(t) and k

(t) are guaranteed to converge to stabilising values.

The mathematical details of the control proof are not reproduced here (see [134, 145]

for details). In practice the equation

k(t) = p

ref

(t)d(t) is used, where  is a diagonal

matrix with entries γ

and γ

. These are convergence coefﬁcients, which determine

the speed of the control action. If they are too large, i.e., if control attempts to force

a response too rapidly, numerical problems may occur and the actuator bandwidth

may become limiting. If they are too small, the controller may not be effective from

within the limit cycle. Guidance on choosing suitable values is provided in [150].

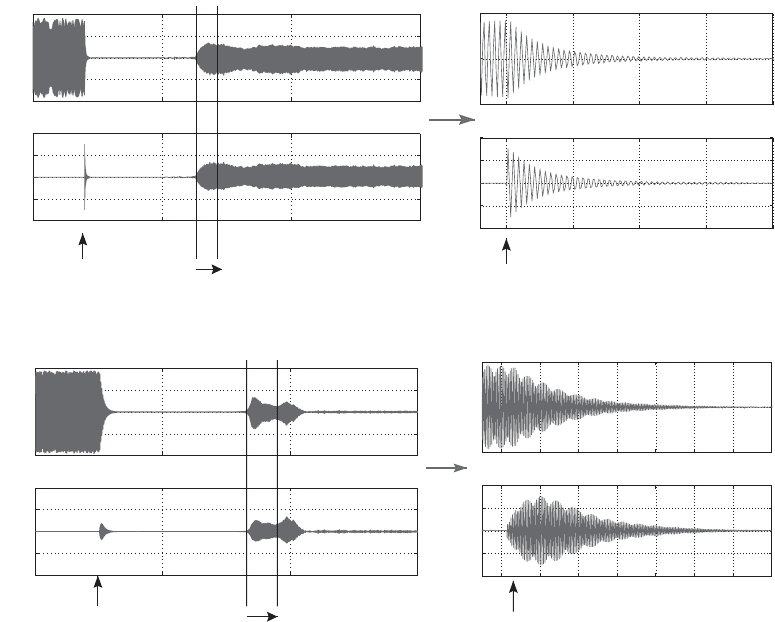
EXPERIMENTAL IMPLEMENTATION OF THE STR. The STR algorithm was implemented

experimentally on the same Rijke tube described in Subsection 3.2.4 [134]. To test

whether it was able to adapt to changes in operating condition, the length L of the

tube was varied by use of the ‘trombone-like’ arrangement to vary the unstable

oscillation frequency. The results are compared with those for a ﬁxed-parameter

phase compensator, of the type designed in Subsection 3.2.4,inFig.3.35. It can be

seen that, although the ﬁxed parameter loses control after the length of the tube is

varied, the adaptive controller maintains control.

The same STR was recently applied to a lean premixed prevapourised combus-

tion rig operating at atmospheric conditions, in which modulation of the fuel supply

was used for actuation [151]. The primary instability was reduced by up to 30 dB, and

initial robustness studies conﬁrmed that the controller retained control for a 20%

change in frequency and a 23% change in air mass ﬂow rate.

Because of their applicability to a wide range of combustion systems and the

fact that stability can be guaranteed, STRs hold real promise in terms of future im-

plementation in full-scale combustion systems. Recent work extended their use to

combustors with higher relative degree and signiﬁcant time delays [134, 152, 153],

combustors exhibiting undesirable reﬂections from boundaries [149], and combus-

tors with an annular shape exhibiting multiple instability modes [150]. Work on how

to extend the adaptive algorithm to more complex combustion systems is ongoing.

FULL-SCALE IMPLEMENTATION OF ACTIVE CONTROL. Although many sophisticated

feedback controllers have been applied to combustion models and laboratory-scale

rigs, there have been very few reported full-scale demonstrations of feedback control.

All used fuel modulation and very simple (and in many ways restrictive) controller

designs.

3.2 Control Strategies for Combustion Instabilities 201

0 5 10 15

−1000

−500

500

1000

Time (s)

0 5 10 15

−4

−2

Time (s)

(Volts)

2 2.05 2.1 2.15 2.2

−500

500

Time (s)

2 2.05 2.1 2.15 2.2

−4

−2

Time (s)

L varied from 75 to 105 cm

control ON

-500

500

Zoom in

2.5 2.6 2.7 2.8 2.9 3 3.1 3.2

−500

500

Time (s)

2.5 2.6 2.7 2.8 2.9 3 3.1 3.2

−1

−0.5

0.5

Time (s)

0 5 10 15

−1000

−500

500

1000

Time (s)

0 5 10 15

−4

−2

Time (s)

control ON

L varied from 75 to 105 cm

control ON

-500

500

Zoom in

(a) Fixed first-order compensator

(a) Adaptive first-order compensator

ref

(Pa)

(Volts) P

ref

(Pa)

(Volts) P

ref

(Pa)

(Volts)

ref

(Pa)

Figure 3.35. Control of Rijke tube under varying tube length L (from [134]).

The ﬁrst full-scale demonstration was in 1988 on the afterburner of a Rolls-

Royce RB 199 military turbofan engine [118]. Actuation was achieved by spilling

fuel from the engine, rather than adding it, using high-response electrohydraulic

servovalves. The modulated fuel was approximately 5%–10% of the mean. Using

a simple gain–time-delay controller, a 12-dB reduction in the dominant low- ‘buzz’

frequency was obtained.

A decade later, active control was performed on a Siemens heavy-duty industrial

gas turbine [117, 154]. The combustor was annular, and the unstable modes were

azimuthal. The pressure at several locations around the combustor circumference

was measured, with a separate control system used at each location. Actuation was

performed by modulating the fuel to the pilot ﬂames by use of a high frequency

solenoid value supplied by MOOG. Simple gain–phase-shift controllers were used,

and the dominant frequency was reduced by 17 dB. It was found that the required

controller parameters changed with operating condition.

Researchers at United Technologies Research Center then demonstrated active

control on full-scale liquid-fuelled lean premixed combustors [124, 155]. With a

solenoid valve to modulate the fuel supply, a 16-dB reduction of the dominant

mode in a single combustor and a 6.5-dB reduction in a 67.5

◦

sector cut from a full

combustor annulus were obtained.

202 Combustion Instabilities

The adaptive phase-shift controller discussed in Subsection 3.2.4 [105] was also

applied at full scale to a Siemens-Westinghouse Dry Low NO

combustor [144]. The

dominant mode was reduced by 15 dB, and the NO

emissions were reduced by

approximately 10%.

3.3 Simulation of Thermoacoustic Instability

By L. Gicquel F. Nicoud and T. Poinsot

As noted in previous sections, thermoacoustic instabilities arise from the coupling

between acoustic waves and ﬂames and can lead to high amplitude instabilities

[29, 74, 75, 156]. In general, these instabilities induce oscillations of all physical quan-

tities (pressure, velocities, temperature, etc.); in the most extreme cases, they can de-

stroy the burner by inducing large-amplitude ﬂame motion ( ﬂashback) or unsteady

pressure (material fatigue). Because the equivalence ratio oscillates when instabil-

ities are present, there is a general trend for combustors to be more unstable when

operating in the lean regime. Also, because of new international constraints, pollu-

tant emissions must be reduced and gas turbine manufacturers need to operate their

systems under leaner and leaner conditions. Consequently there is a need to under-

stand combustion instabilities and to be able to predict them at the design level [157].

The objective in the following subsections is to provide the reader with the rel-

evant information regarding the description, modelling, and computation of thermo

acoustic instabilities. The basic equations are ﬁrst recalled in Subsection 3.3.1. Among

the possible levels of description, two are discussed in more detail in the subsequent

subsections, the large-eddy simulation (LES) approach in 3.3.2 and a 3D linear

description based on the Helmholtz equation in 3.3.3. Because using appropriate

acoustic boundary conditions is critical when analysing combustion instabilities, this

issue is discussed in Subsection 3.3.4. Finally, the different tools and approaches

discussed are used to study the thermoacoustic behavior of an industrial annular

combustor in Subsection 3.3.5.

3.3.1 Basic Equations and Levels of Description

Three types of numerical or semi-analytical methods have been considered so far to

predict and describe these instabilities:

1. LESs of all relevant scales of the reacting, turbulent, compressible ﬂow where

the instability develops. Many recent studies demonstrated the ability of this

method to represent ﬂame dynamics [158–164], as well as the interaction between

reaction zone and acoustic waves [165–168]. However, even when simulations

conﬁrm that a combustor is unstable, LES calculations do not say why and how to

control the instability. Besides, because of its intrinsic nature (full 3D resolution

of the unsteady Navier–Stokes equations), LES remains very CPU demanding,

even on today’s computers (CPU stands for central processing unit).

2. Low-order methods in which the geometry of the combustor is modelled by a

network of homogeneous (constant-density) 1D or 2D axisymmetric acoustic el-

ements for which the acoustic problem can be solved analytically [102, 119, 169–

172]. Jump relations are used to connect all these elements, enforcing pressure

continuity and mass conservation and accounting for the dilatation induced by