Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

3.1 Instabilities in Flames 153

2000

1500

1000

500

–2

–4

–6

–8

0.2 0.4 0.6

0.8

equivalence ratio

1 1.2 1.4 1.6

extinction stretch rate (s

–1

)

Markstein number Ma

Figure 3.1. Markstein numbers (broken lines) and extinction stretch rates (solid lines) under

atmospheric conditions.

counter, or enhance, the Darrieus–Landau (DL) instability. These comprise a con-

ductive energy ﬂux from burned to unburned gas, indicated by the broken arrowed

lines at the leading edge of the ﬂame in Fig. 3.2, and a diffusion ﬂux of the deﬁcient

reactant from the unburned gas into the ﬂame reaction zone, indicated by the solid

lines. The deﬁcient reactant is fuel in the case of a lean mixture and oxygen in the

case of a rich one. The Lewis number, Le =

λ/ρc

D, is a key parameter, where D is

the diffusion coefﬁcient of the deﬁcient reactant. With Le < 1, the ﬂame curvature

focuses diffusion of enthalpy into the ﬂame, shown by the arrowed solid lines. This

exceeds the conductive energy loss out of the ﬂame, shown by the arrowed broken

lines. As a consequence, the local burning velocity increases. An opposite effect oc-

curs in the valley, with a reduction in local burning velocity. As a consequence, the

ﬂame instability is increased further. This TD instability reinforces the DL instability.

Figure 3.2. Development of DL and TD instabilities, after perturbation from a planar ﬂame.

+ and − between perturbed streamlines indicate relative changes of unburned gas pressure.

Arrowed solid lines at the wave crest indicate deﬁcient reactant diffusion; arrowed dotted

lines indicate thermal conduction.

154 Combustion Instabilities

Similar reasoning shows that Lewis numbers greater than unity exert an opposite

and stabilising effect, as does the increase in viscosity with increasing temperature.

The two types of instability are coupled and are hereafter designated by DLTD.

The additional TD term in the instability dispersion relation introduces the

inﬂuences of Le, the unburned to burned gas density ratio σ, ﬂame stretch rate, and

the overall activation energy for the reaction, all acting over a range of wavelengths.

These further complexities make even guideline solutions difﬁcult to obtain. A

successful one was achieved through the linear stability theory of Bechtold and

Matalon [11] for spherical explosion ﬂames. This demonstrates how ﬂames can be

unstable to both types of instability between inner and outer wavelength limits. It led

to a dispersion relationship that expressed the growth of the perturbation in terms

of wave number.

The general approach in [11], now outlined, analyses the perturbation of a spher-

ical ﬂame, including the effect of the changing global ﬂame stretch rate. Perturbed

variables are expanded in spherical harmonic series, and ﬂame instability is investi-

gated over a spectrum of wave numbers. For a ﬂame radius r, with an initial value

signiﬁcantly greater than the ﬂame thickness δ



, the dimensionless amplitude a of

the perturbation relative to r develops according to

a = a

ω(1+/Pe ln R)

. (3.2)

Here a

is the initial value of a and R is r/r

, Pe is the Peclet number deﬁned as

Pe = r/δ



, ω is a growth-rate parameter, which depends on only σ and wave number

n. The expression for  is complex [11]:

 =

β(Le − 1)

ω(σ −1)

, (3.3)

where Q

, Q

are functions of σ, ω, and n, given in [12], and

β, the Zeldovich number,

is deﬁned as

β = T

(

− T

)

The growth rate

A(n) of the amplitude of the perturbation for a wave num-

ber n is expressed by the differential of the natural logarithm of amplitude of the

perturbation with respect to that of Pe. It can be derived from Eq. (3.2) and is

A(n) =

dln(a/a

)

dln(Pe)

= ω



1 −





. (3.4)

The ﬁrst term on the right gives the contribution of the DL instability to the growth

rate, and the second, ω/Pe, gives the contribution of the TD instability. The sign

A(n) depends on that of /Pe and indicates whether the ﬂame is stable. If it is

negative, there is no growth and the ﬂame is stable. If it is positive, the amplitude of

the perturbation grows and the ﬂame is unstable. The critical Peclet number, Pe

,is

reached when, at some value of n(= n

), A(n) ﬁrst becomes equal to zero. This is

the condition that deﬁnes both Pe

and n

. From this and Eq. (3.4),

= . (3.5)

It follows from Eqs. (3.4) and (3.5) that the relative contributions of the DL and TD

instabilities to

(

)

are in the ratio Pe/Pe

. In the absence of instabilities, the inﬂu-

ence of ﬂame stretch rate on the stretched ﬂame speed, dr/dt, is well approximated

3.1 Instabilities in Flames 155

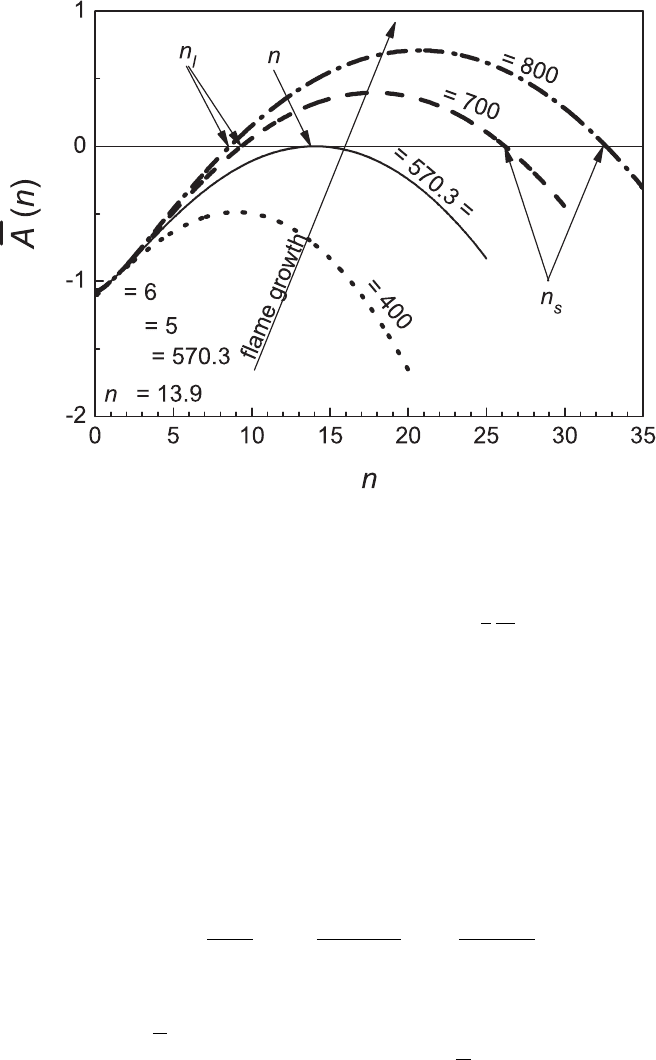
Figure 3.3. Growth rate of perturbation as a function of wave number, σ = 6, Ma = 5.

by a variant of Eq. (3.1), for the ﬂame speed of a spherical ﬂame:

− S = L

∗

, with α

∗

. (3.6)

Here S is the stretched ﬂame speed, S

is the ﬂame speed at zero stretch rate, and L

is the burned-gas Markstein length, which when divided by δ



gives the ﬂame-speed

Markstein number Ma

. When S is linearly extrapolated to α

∗

= 0(r =∞), it yields

Reference [11] does not explicitly employ a Markstein number, based on the

burning velocity as in Eq. (3.1), but in Eq. (3.3)theterm

β(Le − 1) can be linked

to a single Markstein number Ma, as proposed by Clavin [13]. Computed relation-

ships between Markstein numbers based on ﬂame speed and burning velocity are

presented in [14]. From [13],

Ma =

σ −1

ln σ +

β(Le − 1)

2(σ − 1)



σ−1

ln(1 + x)

dx. (3.7)

An improved expression, with allowance for the temperature dependence of the

thermal conductivity

λ, is given in [4].

Variations of

A(n)withn for four different values of Pe are shown in Fig. 3.3 for

σ = 6 and Ma = 5. The dotted line, Pe = 400, shows

A(n) to be always negative for

the full range of n and the ﬂame is stable. As Pe increases, eventually the amplitude

of the perturbation begins to increase and it ﬁrst becomes positive at the critical

wave number n

. The Peclet number at which this occurs is Pe

, which is 570.3 for

the present conditions, with n

= 13.9. When Pe increases above Pe

, there is a range

of wave numbers, between the lower limit n

and the higher limit n

, within which

156 Combustion Instabilities

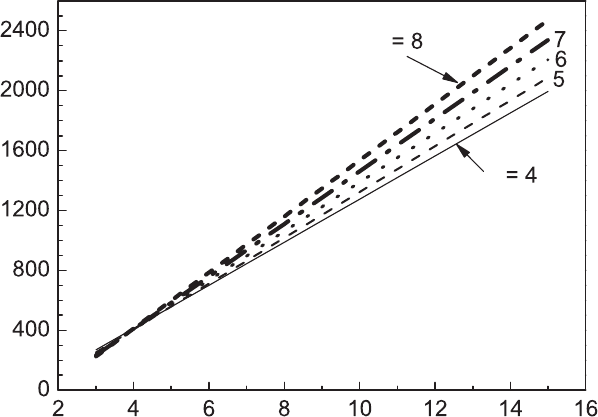
Figure 3.4. Theoretical dependence of Pe

on Ma and σ.

the ﬂame is unstable. The range of unstable wave number broadens as Pe increases,

with the greatest rate of growth of amplitude about midway between these limits.

Computed theoretical values of Pe

for different values of Ma are shown in

Fig. 3.4. The higher the values of Ma and σ, the higher are those of Pe

and, at a

given Pe, the lower are those of n

[15]. All these are factors making for a more

stable ﬂame. The full Bechtold–Matalon theory is valid only for

>30, where

 is

the wavelength normalised by δ



. This which generally corresponds to Ma > 3[15].

The effect of σ is greater at higher values of Ma. When Le is unity, the last term in

Eq. (3.7) becomes zero and only σ has an inﬂuence on Ma. As a result, Ma attains

its lowest values. Furthermore, over the full range of φ for a given fuel, the changes

in σ are relatively small, and the ﬁrst term on the right of Eq. (3.7) changes no more

than a few percent. With little change in Ma, there is negligible change in Pe

with φ,

as indicated by the theoretical plot in Fig. 3.4. This was conﬁrmed experimentally for

near-equidiffusive, spherical, acetylene explosion ﬂames with Le close to unity [16].

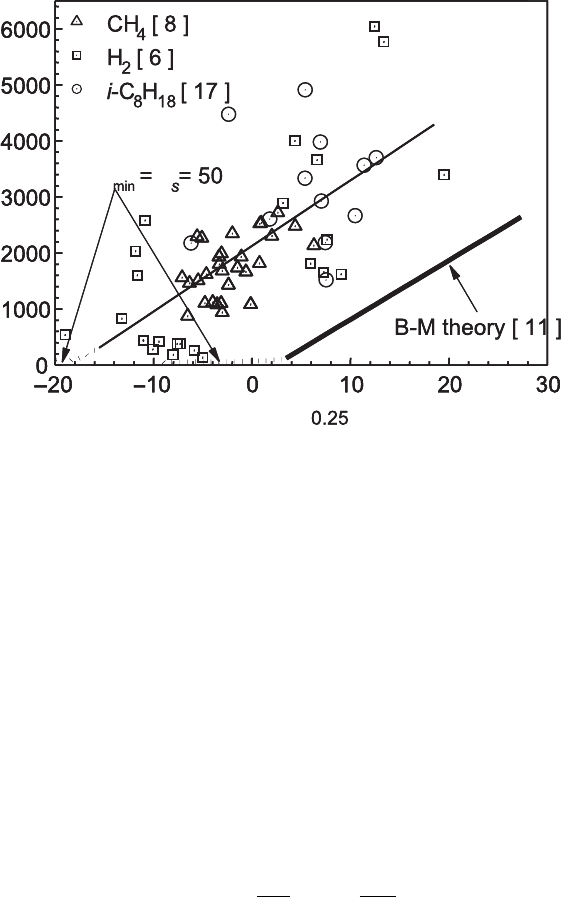
Theoretically predicted values of Pe

are expressed as a function of Maσ

0.25

the bold line in Fig. 3.5. Experimental values, identiﬁed by the initial development

of a full cellular structure, are given by the symbols. These were obtained from

measurements in a spherical explosion bomb with mixtures of methane [8], hydrogen

[6], and i-octane [17] with air at different pressures. There is much scatter in these

experimental values, not only because of the difﬁculty in obtaining accurate values

of Ma, but also in deﬁning precisely the onset of instability, particularly for very

negative Ma

. Such ﬂames become unstable almost immediately. Because of this,

the observed instability of lean H

ﬂames at high pressures questions the concept of

a s table laminar burning velocity under such conditions [6]. Values of δ



are given by

ν/u



. For both experiment and theory, the effect of σ is embodied in the Maσ

0.25

term.

The non-bold, solid line is the best ﬁt to the experimental results. Both lines have

3.1 Instabilities in Flames 157

(Pe

)

Figure 3.5. Measured values of Pe

(symbols) compared with theoretical predictions (bold

line).

almost the same gradient, and the order-of-magnitude difference between them is

attributed to the time lag in the development of a fully cellular ﬂame from an initially

‘cracked’ ﬂame [12]. The lower theoretical value of Pe

is close to the point at the

ﬁrst ‘cracking’ on the ﬂame surface. The higher experimental value is identiﬁed by

the full development of a cellular structure and the increase in the ﬂame speed that

results from the wrinkling of the ﬂame surface.

Because of the importance of ﬂame stretch rate in stabilising a ﬂame, the critical

value of a dimensionless group based on this might be of more general utility than

one based on ﬂame radius. Hence the laminar Karlovitz stretch factor at criticality,

, equal to α

∗

(δ



), was evaluated, where α

∗

is the total stretch rate at Pe

.With

Eq. (3.6) applied to this condition and the relationship S

= σu



at constant pressure

and zero stretch rate, it is readily shown that

2 σ



1 + 2



−1

. (3.8)

Values of K

, found from the experimental values of Pe

in Fig. 3.5, are indicated by

crosses and plotted against Ma

in Fig. 3.6. The larger circle symbols show additional

ethanol–air data from [18]. A best-ﬁt curve to all the data is shown in Fig. 3.6 by the

lower solid line curve in the plot of laminar Karlovitz stretch factor, K



= α

∗



/δ



against Ma

and given by

= 0.0075 exp (−0.123 Ma

). (3.9)

The regime of unstable ﬂames lies below this curve. Above it, the value of



is sufﬁcient to stabilise the ﬂame. Also shown are the values of the turbulent

Karlovitz stretch factor, K

0.8

, at which the probability of a turbulent ﬂame being able

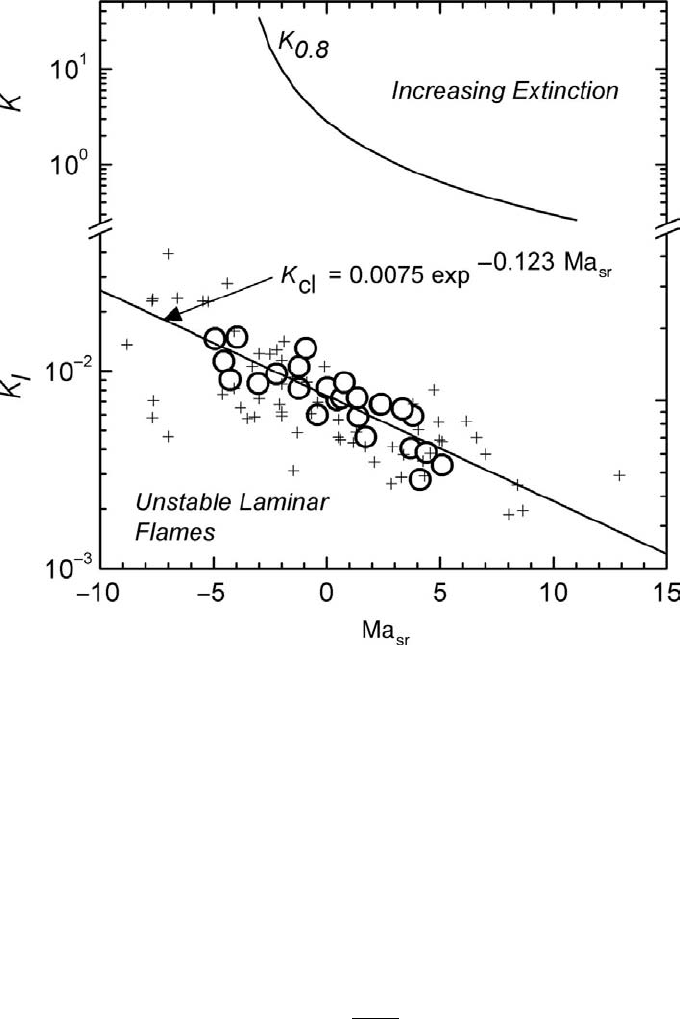
158 Combustion Instabilities

Figure 3.6. Limit of instability for laminar ﬂames, K

on K



scale, and onset of ﬂame extinc-

tion in turbulent ﬂames, K

0.8

on K scale.

to propagate is reduced to 0.8. This is due to the onset of ﬂame extinction arising

from the higher stretch rate. This is discussed in Subsection 3.1.2.

PENINSULA OF INSTABILITY AND INCREASING FLAME SPEED. It was shown in [12] that

the theoretical results from [11] could be presented as a peninsula of instability,

bounded by n

and n

and also dependent on Pe and Ma

, as indicated in Fig. 3.7.As

decreases, fn

increases, Pe

decreases, and the area of the peninsula increases.

The relationship between wave number n and the wavelength normalised by δ



,is

n =

2π Pe



. (3.10)

Allowance for the experimentally observed lag between the theoretical value of Pe

and the onset of a fully cellular ﬂame was made in [12] by multiplying the theoretical

value of the upper-limit wave number n

by a lag factor of less than unity, f .This

was evaluated at the measured Pe

by equating fn

s,cl

to the known theoretical value

of the lower-limit wave number n

l,cl

, where the subscript cl indicates a value at the

measured Pe

3.1 Instabilities in Flames 159

wave number

Peclet number

)

(f n

)

Figure 3.7. Instability peninsula, with limiting wave numbers at constant Ma

.AsMa

de-

creases, so does Pe

, whereas

(

dfn

/dPe

)

increases.

For Pe > Pe

the theory shows n

to increase close to linearly with Pe. This

linearity is maintained for the modiﬁed wave number, fn

,asshowninFig.3.7 and

given by [12]

= fn

s,cl

(

Pe − Pe

)

d fn

dPe

. (3.11)

With Eq. (3.10) applied to experimental conditions, dfn

/dPe = 2 π/



, and this

increases as Ma

decreases. A limit to the gradient is set by the ﬁnite thickness of the

ﬂame, and experiments suggest a lower limit to the value of



of about 50 at very

negative values of Ma

[19]. This results in a maximum value of dfn

/dPe = 2π/50.

At this limit, the experiments show that a high negative ﬂame stretch causes localised

ﬂame extinctions at the cusps. They also suggest a threshold for the onset of localised

extinctions that begin to reduce the expected burning rate of the wrinkled ﬂame at

about



= 167.

As a ﬂame grows in size,



, the shortest wavelength, remains constant, whereas,

from Eq. (3.10), the longest wavelength,



, might be expected to be proportional to

Pe, with consequently very little change in n

. As the ﬂame propagates, it is wrinkled

by an ever-increasing range of wavelengths, which is due entirely to the increase in



The evolution of the associated cellular structure that exists through the peninsula

was traced in detail in [17]. Newly formed cells are initially stabilised by the localised

stretch rate, but, as they grow in size, their stretch rate decreases because of the

decreasing curvature. Eventually, at a critical localised Peclet number or Karlovitz

160 Combustion Instabilities

stretch factor, an instability arises at the growing cell and the original cell ﬁssions

into smaller cells. The newly formed smaller cells are initially stabilised by their

high curvature and the greater stretch rate. They grow in size, and the evolutionary

cycle is repeated. By these means, the original instability is re-stabilised through the

formation of a cellular structure over the entire ﬂame surface.

The increased wrinkling of the ﬂame surface with increasing Pe results in an

increasing ﬂame speed that can be estimated from fractal considerations [12]. These

suggest that the ratio of the fractal surface area with a resolution of the inner cut-off

to that with a resolution of the outer cut-off, at Pe, is

(

)

D−2

, where

D is the

fractal dimension. If Pe is large enough for ﬂame stretch rates to be relatively small,

ﬂame speeds are proportional to the surface area. Consequently this ratio is equal

to the ratio F of ﬂame speeds, with and without instabilities. The former is indicated

by S

and the latter by S

(= u



σ). The unstable ﬂame speed S

is equal to dr/dt,

where r is the mean ﬂame radius of the wrinkled surface. Hence, at a given Pe, with

D = 7/3,

F =





σ u



dPe





1/3

, (3.12)

in which S

= u



σ, δ



= ν/u



, and t = tu



/ν, where ν is the kinematic viscosity. The

value of F increases with the range of unstable wavelengths, which increases as Ma

becomes more negative and Pe increases. The last is further increased with increasing

pressure because of the decrease in δ



With these conditions and d(fn

)/d Pe assumed to be constant, Eqs. (3.11)

and (3.12), after appropriate integration, yield, in the unstable regime [12, 15],

Pe = Pe

+ Bt

3/2

, (3.13)

where Pe

is the value of Pe at t = 0 and it can be relatively close to Pe

.The

numerical constant B depends on σ and Ma

, particularly through the gradient

dfn

/dPe.From[15],

B =







3/2



dPe



0.5



. (3.14)

It is readily shown from Eq. (3.13) that

dPe

2/3

(

Pe − Pe

)

1/3

, (3.15)

and also from Eqs. (3.12) and (3.13) that

F =

2σ

t =

2σ

2/3

(

Pe − Pe

)

1/3

. (3.16)

In the earlier nonlinear theory of [20] the ﬂame radius also varied as t

3/2

, and

Eq. (3.13) was applied to large-scale explosions [21, 22]. There are problems in the

DNS of the self-acceleration of unstable ﬂames because of the generation of numer-

ical noise [23]. The simulations in [23] showed that, after an initial acceleration, 2D

expanding ﬂames slow down to a constant speed, whereas spherical ﬂames continue

to accelerate. For the latter, over the computed period of time of the acceleration,

the optimal exponent for

t was 1.32.

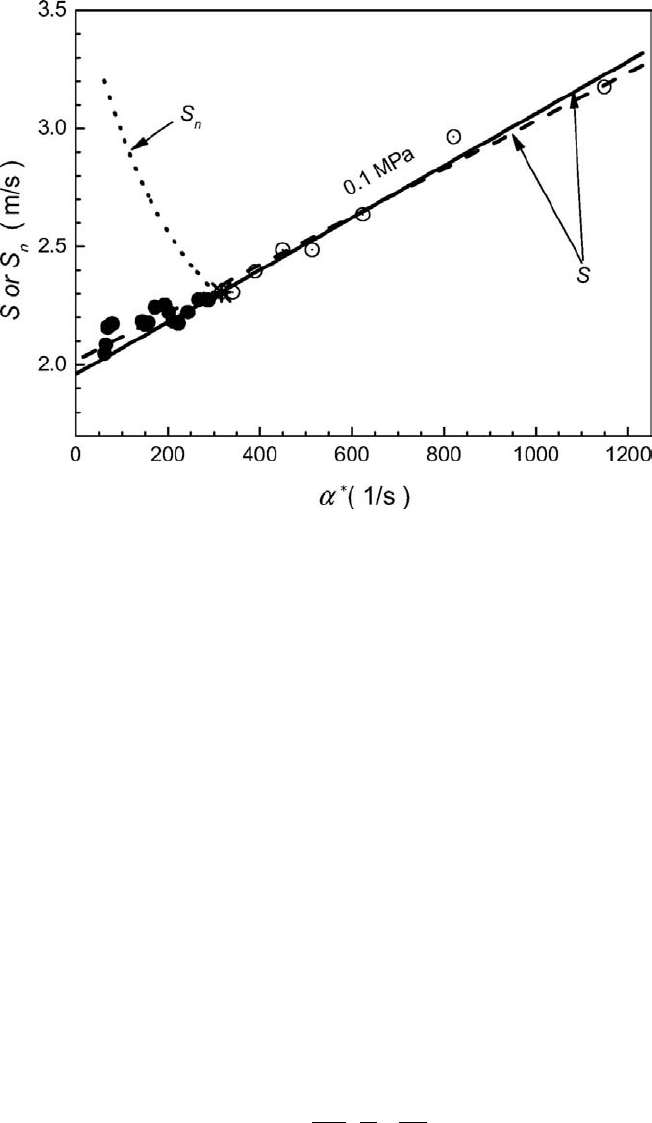
3.1 Instabilities in Flames 161

Figure 3.8. Variations of ﬂame speeds S and S

with ﬂame stretch rate, α

∗

= (2/r)S,for

0.1MPa,φ = 0.4, T = 365 K, from [6].

The changes in ﬂame speed with α

∗

during an experimental spherical explosion

of a lean H

–air mixture at 0.1 MPa, T = 365 K, φ = 0.4, are shown in Fig. 3.8 [6].

The Markstein number is negative, initially the ﬂame is stable, and the open symbols

show the stretched ﬂame speed S decreasing with α

∗

prior to the development of

instabilities when α

∗

decreases below about 350 s

−1

. The unstable ﬂame speed S

shown by the dotted curve, increases sharply as the ﬂame propagates more rapidly

as a result of its increasing cellularity. The enhancement of ﬂame speed that is due to

cellularity was found with Eq. (3.12), from which the theoretical stable ﬂame speed,

shown by the black circular symbols in Fig. 3.8, could be found. Extrapolation of the

stable, stretched, ﬂame speed to zero stretch rate gave S, which when divided by σ

yielded u

ell

ACOUSTIC WAVES GENERATED BY BURNING-RATE ACCELERATION. The higher the

burning velocity, the higher the net rate of volume generation at the reaction front,

dV/dt. A rapid rate of change in this rate can induce appreciable acoustic waves.

At a sufﬁcient distance d from a part of a ﬂame or an entire small ﬂame surface,

the noise approximates that from a monopole sound source. Simple acoustic theory

gives the associated instantaneous sound pressure p(t) above the ambient at time

t. From Hurle et al. [24], this is

p(t) =

4πd









t−t

, (3.17)

where t

is the time for the sound wave to propagate the distance d from the source

to its measurement point through a non-reacting gas of density ρ. Values of p(t),

162 Combustion Instabilities

predicted from measurements of the rate of change of C

emission intensity in

an explosion of a 4-cm-diameter soap bubble of stoichiometric ethylene–air, were

conﬁrmed [24 ] by microphone measurements 0.33 m away. A pressure pulse of 3 Pa

was recorded at the end of combustion, after which p(t) fell to zero before reaching

a minimum value of −5 Pa in a rarefaction wave.

If A is the area of the reaction front propagating relative to the unburned gas

at a burning velocity u

, then the volumetric rate of consumption of unburned gas

is Au

. The corresponding volumetric rate of production of burned gas is greater in

the ratio of unburned-gas to burned-gas densities σ. Hence the net rate of volume

generation that is due to reaction is

= Au

(σ −1) . (3.18)

Arising from this expression, mass conservation and the deﬁnition of u

lead

to a propagation speed relative to the ﬁxed radial stationary coordinates of u



σ and,

following Eq. (3.12),

= u

σ = u



dPe

. (3.19)

In Eq. (3.17) for a truly monopole source, in which the total sound pressure is a

simple sum of the component pressures from all ﬂame elements, the overall size of

the ﬂame, or part of it, must be restricted. In [24],thesizeisrestrictedtoaquarter

wavelength of the acoustic wave. In addition, the compression and expansion of the

acoustic wave are assumed isentropic. This becomes less justiﬁable as p(t) becomes

large. For a spherical ﬂame of radius r,Eqs.(3.18) and (3.19)give

= 4πr

(σ −1) = 4πr

σ −1

. (3.20)

For large ﬂames there can be differences in the time intervals t

originating at

different points in the ﬂame and their arrival time at the ﬁxed measurement point.

Allowance can be made for this by expressing Eq. (3.17) in integral form. Here

simpliﬁed solutions are presented. These assume the same value of dr/dt throughout

the ﬂame at a particular instant and a ﬁxed value of d, measured from the centre of

the spherical ﬂame. Starting with Eq. (3.20) and involving Eqs. (3.13) and to (3.19),

it can be shown that at the average dimensionless distance,

d = d/δ



, the averaged

overpressure in an unconﬁned explosion is

p

ρu



Pe B

4/3



σ −1



3(Pe − Pe

)

2/3

2(Pe − Pe

)

1/3



. (3.21)

The ﬁrst term within the square brackets arises from the rate of change of ﬂame

area, the second from the rate of change of ﬂame speed. The mean dimensionless

time for an acoustic wave to propagate the average distance d from the centre of the

spherical ﬂame at the acoustic velocity

c is



. (3.22)

The duration of ﬂame propagation in the unstable regime to Pe is found from

Eq. (3.13). This time, added to

, gives the time from the onset of the instability to

the elevation p at the distance

d. The expressions for p and F were evaluated