Swaminathan N., Bray K.N.C. (eds.) Turbulent Premixed Flames

Подождите немного. Документ загружается.

2.4 Transported Probability Density Function Methods 123

500

1000

1500

2000

500

1000

1500

500

1000

1500

T (K)

x75(%)

500

1000

1500

0.5

r/D

500

1000

1500

0.5

1.5

r/D

x/D=10.5

x/D=8.5

x/D=6.5

x/D=4.5

x/D=2.5

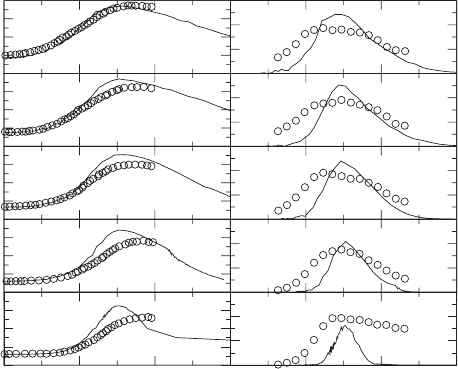
Figure 2.33. Mean temperature and OH mass fraction for a stoichiometric CH

/–air mixture

at Re = 52 500 [211]. Transported PDF calculations with modiﬁed Curl’s model [254]and

Eq. (2.155) with C

∗

= 1.2andC

= 4(—)andT

= 1785 K. Experimental data ( ◦)from

Chen et al. [256].

two computations with higher time-scale ratios burn stably. It is also evident from

the reaction progress variable that the pilot ﬂame temperature is too high. How-

ever, computations with T

= 1785 K lead to extinction over an extended range

of values of C

. The computations thus indicate more extensive ﬂame-stabilisation

problems than observed experimentally. The inﬂuence of the extended SDR closure

[Eq. (2.155)] can, however, be expected to be signiﬁcant in the early part of the

ﬂame. Based on the experimental data, u

can be estimated to be O(1) close to

the nozzle. It may also be noted that, despite the apparent overprediction of temper-

ature, the computed peak OH concentrations are well reproduced. This is surprising

as there is a direct sensitivity of OH levels to temperature, as shown in Fig. 2.32.The

comparatively high value of C

required in the current ﬂame, compared with diffu-

sion ﬂames [295], may at ﬁrst be somewhat surprising. However, given that typically

2.6 ≤ C

≤ 4.0 [17 ], the reported values of C

are not inconsistent.

The experimental study of O’Young and Bilger [156] indicates that the velocity–

scalar time–scale ratio varies signiﬁcantly as a function of the Damk

ohler number

and increases by almost an order of magnitude as Da →∞. As just discussed, the

inﬂuence is likely to be particularly strong in the proximity of the pilot ﬂame and

thus close to the burner surface. Accordingly, the functional form of Eq. (2.155)was

explored with a pilot temperature of T

= 1785 K and with C

= 4 and C

∗

= 1.2.

The choice of modelling constants thus corresponds to that used in the simulations

shown in Fig. 2.21. As previously mentioned, the computational ﬂame could not be

stabilized with C

∗

= 0 under these conditions. The level of agreement is arguably

signiﬁcantly improved, though some level of overprediction remains, as shown in

Fig. 2.33. The discrepancies between the measured temperature and OH proﬁles,

also previously discussed, are readily apparent. However, the current closure at the

joint scalar level has a tendency to produce thinner ﬂames [17] and the presence on

124 Modelling Methods

0.0 1.0 2.0 3.0 4.0

(cm/s)

0.2 0.4 0.6 0.8 1.0

stoic

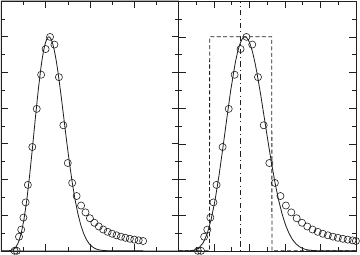
Figure 2.34. Proﬁle of laminar burning veloc-

ities obtained for a CH

(1:1) mixture at

varying equivalence ratios (left) and shown

against mixture fraction for the φ = 3.2ﬂame

(right) [257]. The symbols represent the nu-

merical results, and the solid line is a ﬁt using a

β-function.

non-gradient transport effects cannot be ruled out – particularly in the vicinity of the

burner. However, it appears clear that the extended algebraic closure for the SDR

carries potentially signiﬁcant beneﬁts in the context of the computation of mixing

frequencies and that the inclusion of more comprehensive chemistry permits the

computation of the thermochemical structure of high-Reynolds-number premixed

ﬂames.

2.4.10 Partially Premixed Flames

The closure applied to compute the premixed ﬂames in the previous section was

also used by Lindstedt et al. [257] to investigate piloted partially premixed CH

–

–air turbulent jet ﬂames at high Reynolds numbers (Re ≈ 60 000 and 67 000) for

two equivalence ratios, φ = 2.1 and φ = 3.2. The ﬂames were studied experimentally

at Sandia National Laboratories and were well characterised close to the nozzle

through multiscalar measurements for 1 ≤ x/d ≤ 4. The ﬂames offer the opportu-

nity of computational investigations of their thermochemical structure close to the

burner. Moreover, the data sets are ﬁnely spaced through the local extinction region.

The current aim is to provide further examples of the impact of closure approxima-

tions for the SDR. The effects of variations in the time-scale ratio (2.3 ≤ C

≤ 4) in

Eq. (2.152) were thus investigated along with the impact of the extended algebraic

relationship shown in Eq. (2.155). The laminar burning velocity required in the latter

closure was obtained from the corresponding premixed laminar ﬂames with a fuel

stream of 50% H

and 50% CH

, giving a value of 0.6 m/s. The value C

∗

= 1.2was

retained from previous work [210, 211].

Lindstedt et al. [257] evaluated two approaches for the extension of Eq. (2.155)

to partially premixed combustion. In the ﬁrst, the stoichiometric value of the burn-

ing velocity was used to determine the time-scale ratio in the ﬂammability region

± Z, where Z = 0.5 Z

) with the term set to zero elsewhere by means of

Heaviside functions at the edges of the ﬂammability range. The approach was found

to overestimate the inﬂuence of the term; u

(φ) was also computed, and the resulting

shape was represented by a β function [257]. The resulting expressions are shown

in Fig. 2.34, and the ﬁtted function was judged to provide a sufﬁcient match in the

critical regions of scalar mixing (φ ≤ 1.6).

2.4 Transported Probability Density Function Methods 125

500

1000

1500

2000

2500

500

1000

1500

2000

2500

Temperature (K)

0.0 0.2 0.4

0.6

0.8 1.0

Mixture Fraction

500

1000

1500

2000

2500

0.2 0.4

0.6

0.8 1.0

Mixture Fraction

0.2 0.4

0.6

0.8 1.0

Mixture Fraction

pilot

= 10.2 m/s

pilot

= 7.4 m/s

pilot

= 8.2 m/s

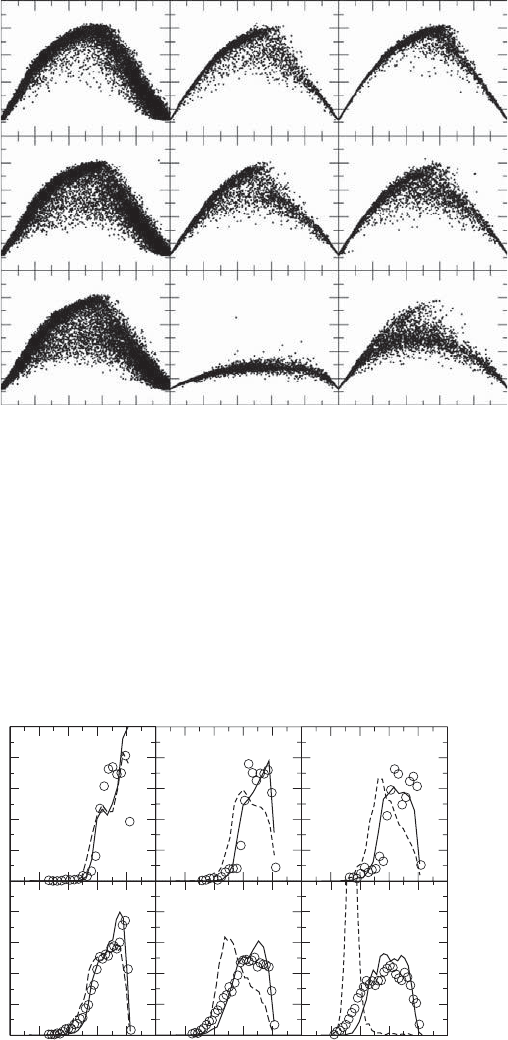
Figure 2.35. (Left) measurements and computations of temperature in mixture fraction space

in a φ = 2.1ﬂameatx/d = 4 for three pilot settings using (middle) a constant time–scale ratio

of C

= 3.0 and (right) the extended algebraic relationship with C

= 2.3andC

∗

= 1.2[257].

The value of C

(with C

∗

= 0) was varied in the range 2 .3 ≤ C

≤ 4.0 as several

ﬂames extinguished early with the ‘standard’ value of 2.3 used in earlier studies,

e.g., [233, 234]. Raising the value to 3.0 promoted burning and led to better predic-

tions for most cases, as shown in Figs. 2.35 and 2.36. However, the extinction kernel

was still overextended unless a strong pilot was used, and the sensitivity to successive

0.0005

0.0010

0.0015

0.0020

0.0025

Conditional PDF

0.0

0.5

1.0

1.5

2.0

2.5

0.0000

0.0005

0.0010

0.0015

0.0020

0.0025

0.5

1.0

1.5

2.0

2.5

T × 10 (K)

0.5

1.0

1.5

2.0

2.5

<x/d=2>

<x/d=4>

<x/d=2>

<x/d=4>

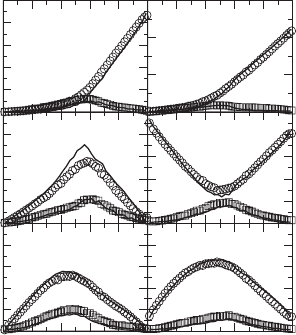
Figure 2.36. Conditional PDFs (Z

± Z,whereZ = 0.5 Z

) of temperature for the φ =

2.1ﬂameatx/d = 4 for (left) V

pilot

= 10.2, (middle), V

pilot

= 8.2, and (right) V

pilot

= 7.4[257].

The symbols represent experimental data, and the lines are predictions of the extended

algebraic relationship with (—) C

= 2.3andC

∗

= 1.2 and (- - -) the modiﬁed Curl’s model

with C

= 3.0.

126 Modelling Methods

0.02

0.04

0.06

0.08

0.10

0.005

0.010

0.015

0.01

0.02

0.03

0.04

0.05

0.050

0.100

0.150

0.200

0.250

0.0 0.2 0.4

0.6

0.8 1.0

Mixture Fraction

0.00

0.02

0.04

0.06

0.08

0.10

0.2 0.4

0.6

0.8 1.0

Mixture Fraction

500

1000

1500

2000

2500

T (K)

Figure 2.37. Conditional means and rms of tem-

perature and species mass fractions for the φ = 2.1

ﬂame with V

pilot

= 7.4m/satx/d =4[257].

reductions in the pilot velocity was not predicted accurately. A value C

= 4.0 caused

burning for all cases, though the validity of applying such a high value, compared with

the standard  2.0, is questionable and may lead to an inappropriate downstream

evolution of the variance.

An advantage of the extended algebraic expression is that the time–scale ratio

increases conditionally in the ﬂame zone and that other parts of the ﬂow remain

unaffected. The results obtained are also shown in Figs. 2.35 and 2.36. The ﬁndings

are encouraging in the sense that the progressive extinction patterns are captured.

However, the tendency of the extended model to underpredict extinction at the

highest pilot velocity is shown by the slightly elevated temperatures on the rich side.

There is also a tendency to promote too much extinction at the lowest pilot velocity.

Nonetheless, scatter plots of temperature, as shown in Fig. 2.35, clearly show the

extent to which the closure is able to reproduce the sensitivity to changes in the pilot

velocity. The improvement is also apparent in the conditional PDFs of temperature

shown in Fig. 2.36.

The ability of the transported PDF method to correctly predict species mass

fractions is highlighted in Fig. 2.37, which shows the most extreme pilot case for the

φ = 2.1 ﬂame. The trends are encouraging, though a modest overprediction of CO

appears as a result of the elevated temperatures on the rich side of the ﬂame. Clearly

some inadequacies remain, though the results do indicate signiﬁcant improvements

compared with the standard closure.

2.4.11 Scalar Transport at High Reynolds Numbers

Ferr

ao [296] and Duarte et al. [297] studied scalar transport in lean highly sheared

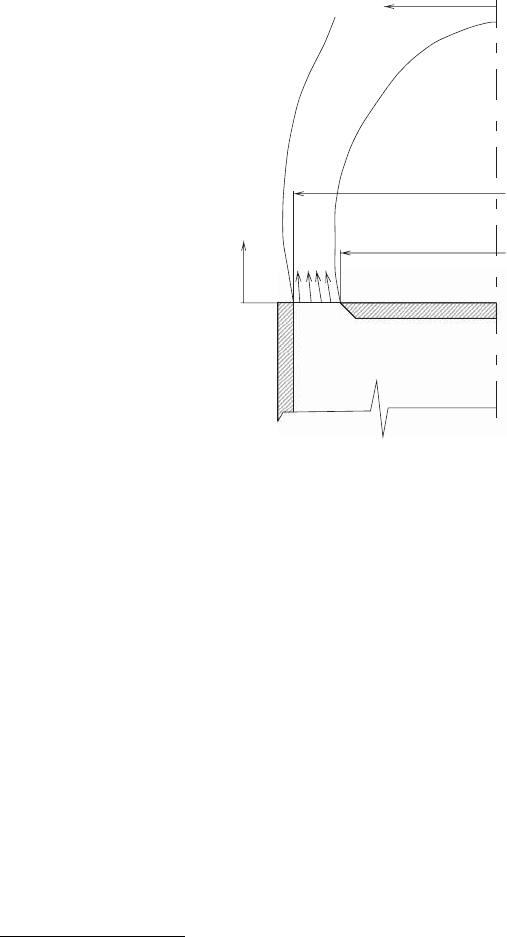
premixed turbulent propane ﬂames, and a schematic picture of the geometry is

presented in Fig. 2.38. The case discussed here features a mean inlet velocity of

= 42.4ms

−1

resulting in a Reynolds number of 154 000. The Reynolds number of

turbulence, estimated [296]withu

rms

≈ 0.14U

and an integral length scale  ≈ d/2,

was Re

≈10 800. The ambient temperature was 303 K, and the adiabatic ﬂame

temperature for φ = φ

= 0.55 was reported as 1617 K, which agrees well with the

2.4 Transported Probability Density Function Methods 127

Ψ=1

air

Ψ=0

, u

r, v

= 56mm

C + air

(φ = 0.55)

= 80mmD

U = 42.4m/s

Figure 2.38. The experimental geometry of Ferr

ao [296] (not

to scale) [283]. The ﬂow pattern is indicated by the dividing

streamlines and values of the normalised mean stream func-

tion !. The streamline deﬁned by ! = 0markstherecircula-

tion bubble.

value of 1596 K obtained in laminar ﬂame calculations using detailed chemistry. The

transported PDF approach closed at the joint velocity–scalar level was applied [283]

with different velocity closures to explore the impact on scalar transport: (1) The

k- model, ( 2) the GLM of Haworth and Pope [248], and (3) the GLM with the

preferential acceleration term removed [see Eq. (2.151)].

The principal aim was to explore the impact of turbulent transport, and hence

a simpliﬁed chemical source term, based on detailed chemical kinetic laminar ﬂame

solutions, was used for the scalar c. However, the ﬂame under consideration is

not purely premixed and dilution by ambient entrained air must be considered.

Assuming equal diffusivities of species, a conserved scalar z can be deﬁned that

takes zero value in air and unity in the reactant mixture (φ = φ

). Only very lean

mixtures (φ ≤ φ

= 0.55) are considered. The reactive scalar c is deﬁned as a ‘global’

reaction progress variable. Its deﬁnition is based on the mass fraction of O

converted

to products at a particular value of Z and made non-dimensional by the maximum

mass fraction of O

available for conversion into products (i.e., at Z = 1) as outlined

by H

ulek and Lindstedt [255]:

c =

Z=ξ

− Y

Z=1

− Y

Z=1

. (2.169)

An analysis of detailed chemical kinetic solutions of relevant lean propane–air ﬂames

shows that a reaction progress variable deﬁned in the manner of Eq. (2.169) has the

practical advantage in that the gas temperature is, to a very good approximation,

linear in c and almost independent of the value of z.Ifτ = τ|

Z=1

= (ρ

/ρ

Z=1

− 1is

the maximum expansion ratio (for Z = 1 and thus φ = φ

), then the gas density can

be written in the customary manner [ ρ = ρ

/(1 + τc)]. The maximum temperature

of the burnt gases is approximately linear in Z and c

max

(ξ) = ξ. As a consequence,

the scalar c has the properties of a standard reaction progress variable (e.g., [7])

except that its upper bound depends on the local stoichiometry. The resulting region

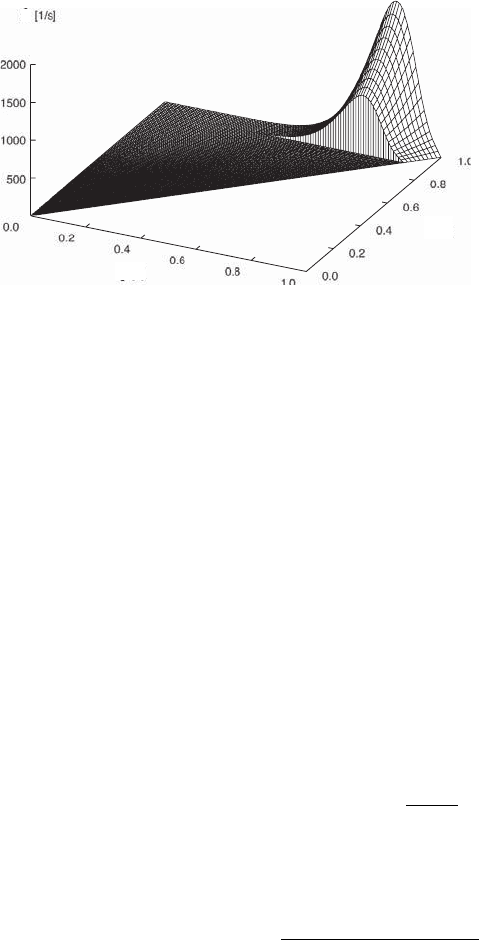
128 Modelling Methods

Figure 2.39. A 3D plot of the source term for the reaction progress variable c as a function

of ξ and ζ [see Eq. (2.170)] [283].

of allowed compositions forms a triangle in ξ–ζ space, deﬁned by 0 ≤ ζ ≤ ξ and

ζ ≤ ξ ≤ 1.

The practical ﬂammability limit was set to φ

= 0.50, which corresponds to

≈ 0.91. Reaction rates based on the depletion rate of O

[i.e., consistent with

Eq. (2.169)] were extracted from laminar ﬂame calculations for stoichiometries

φ = 0.50, 0.52, and 0.55. The shape of the source term does not depend strongly

on stoichiometry, and the value for the local reaction progress variable ˆζ = ζ/ξ scales

with the laminar burning velocity as u

as shown by Spalding [298]. The laminar burn-

ing velocity can be approximated as a linear function of ξ with the parameterisation

of the chemical source term:

(ξ, ζ) =

(ξ, ˆζ)ifξ ≥ ξ

0ifξ<ξ

, (2.170)

where S

(ξ, ˆζ) is the chemical source term for the local-stoichiometry-based reaction

progress variable (bounded between 0 and 1), obtained as

(ξ, ˆζ) = S

(ˆζ)|

ξ=1



ξ=1



. (2.171)

The value of u

was ﬁtted as a linear function of Z, and the function S

(ˆζ)|

Z=1

was

approximated with a least-squares ﬁt.

(

c)|

Z=1

= (1 −



exp



+ a

c + a

+ a

1 + a

c + a

+ a



− exp(a

)



. (2.172)

The shape of S

(ξ, ζ)witha

=−2.219641, a

=−0.566512, a

= 26.17081, a

−1.294479, a

=−39.28250, a

= 0.87046, and a

= 15.44937 is illustrated in

Fig. 2.39. The source term falls rapidly as ξ approaches the limit and at ξ = ξ

the

peak rate is only 40% of the maximum at ξ = 1.

The molecular transport in Eq. (2.144) was closed with the binomial Langevin

model [250] extended to account for joint velocity–scalar statistics and multiple

scalars, as described by H

ulek and Lindstedt [255]. The functional forms for the

diffusion (B

) and drift (G

) coefﬁcients are given in Appendix 2.D. The decay

time scale of scalar ﬂuctuations [τ



2



/(2







)] was estimated by Eq. (2.152)

2.4 Transported Probability Density Function Methods 129

0.00 0.02 0.04

0.06

0.08

r (m)

0.0

0.2

0.4

0.6

0.8

1.0

Figure 2.40. Radial proﬁles of the mean re-

action progress variable



c at x = 0.081 m.

Experimental data (symbols) [296] com-

pared with predictions obtained with (– –)

the k- model; (—) the GLM; (– · –)

the GLM without preferential acceleration

terms (2.151)[283].

with τ

= τ

, where τ



k/ and the coefﬁcient had the standard value of

= 2[91 ].

The treatment of boundary conditions was outlined by Hulek [283], and experi-

mental proﬁles obtained at x = 10 mm were used to derive an estimate at x = 0mm.

The distance of 10 mm was relatively small compared with the diameter of the jet,

and the ﬂow was considered to be locally parabolic. Following translation along the

experimentally determined mean streamlines, the proﬁles measured at x = 10 mm

were used for in-ﬂow boundary conditions between d = 56 mm and D = 80 mm at

x = 0 mm (see Fig. 2.38). Solid boundaries at x = 0 mm were treated with the wall-

functions approximation in the ﬁnite-volume part of the algorithm, and the no–slip

specular-reﬂection boundary condition [299] was used for the Lagrangian particles.

Information relating to the the ﬂame shape can be obtained from radial proﬁles



c. Comparisons of predictions with the experiment at x = 0.081 m are shown in

Fig. 2.40. Two features are worthy of comment. First, the position of the ﬂame is

predicted accurately by the second-moment-based model provided that preferential

acceleration is included. By contrast, the k-ε model gives a ﬂame brush that is located

too close to the symmetry axis, and the same problem prevails for the second-moment

closure with the preferential acceleration term removed. Secondly, the shape of the

mean reaction progress variable is not well reproduced by the eddy viscosity closure.

The impact of preferential acceleration on the turbulent scalar ﬂux is clearly

noticeable in Fig. 2.41, which shows the radial component of the scalar ﬂux





at the same locations. Similar observations can be made from the



c(r) proﬁles at

x = 0.114 m, shown in Fig. 2.42, and the corresponding scalar ﬂux shown in Fig. 2.43.

0.00 0.02 0.04

0.06

0.08

r (m)

0.0

0.5

1.0

1.5

c"v" (m s

–1

)

Figure 2.41. Radial proﬁles of the radial com-

ponent of the turbulent scalar ﬂux





x = 0.081 m [283]. Lines and symbols are as

in Fig. 2.40.

130 Modelling Methods

0.00 0.02 0.04

0.06

0.08

r (m)

0.0

0.2

0.4

0.6

0.8

1.0

Figure 2.42. Radial proﬁles of the mean

reaction progress variable



c at x = 0.114 m

[283]. Lines and symbols are as in Fig. 2.40.

Measurements of the scalar–velocity correlation are very difﬁcult to perform, and

one should exercise caution when making quantitative comparisons. Nevertheless,

it is obvious that neglecting preferential acceleration results in the magnitude of the

ﬂux being overpredicted by a large margin. Interestingly, the k-ε model also predicts

very high values of the turbulent scalar ﬂux (the PDF solution in this case includes

the effect of preferential acceleration). An explanation can be found in the turbulent

kinetic energy proﬁles at x = 0.081 m in Fig. 2.44 – both the k-ε model and the second-

moment model without preferential acceleration overpredict the



k values close to the

symmetry axis. A higher level of turbulence means a stronger generation of gradient-

wise scalar transport (by means of the term











∂



c/∂x



) and thus more gradient

diffusion. Farther downstream, all predictions are characterised by a too-low value of



k at the centreline, as shown in Fig. 2.45. Nevertheless, predicted values in the shear

layer where the ﬂame is located are adequate, and comparisons with experimental

data suggest that preferential acceleration effects and non–gradient diffusion exert

a signiﬁcant inﬂuence at high Reynolds numbers and need to be taken into account

to ensure accurate modelling of velocity statistics under the current conditions.

2.4.12 Conclusions

In this chapter the ability of the transported PDF approach to reproduce the char-

acteristics of stable premixed turbulent ﬂames and those close to extinction was

assessed at different closure levels. Predicted turbulent burning velocities depend

0.00 0.02 0.04 0.06 0.08

r (m)

0.0

0.5

1.0

1.5

c"v" (m s

–1

)

Figure 2.43. Radial proﬁles of the radial

component of the turbulent scalar ﬂux





at x = 0.114 m [283]. Lines and symbols are

as in Fig. 2.40.

2.4 Transported Probability Density Function Methods 131

0.00 0.02 0.04

0.06

0.08

r (m)

100

150

k (m

–2

)

Figure 2.44. Radial proﬁles of the kinetic en-

ergy of turbulence



k at x = 0.081 m [283].

Lines and symbols are as in Fig. 2.40.

on the structure of the model for turbulent transport in scalar space (i.e., the struc-

ture of the prescribed mixing transition density function) and on the magnitude of

the relevant (mixing) time scale. Examples given suggest that the effects of closure

approximations for the SDR do have a signiﬁcant inﬂuence on computed ﬂame

properties. An extended multiscale algebraic model, derived to account for small-

scale properties, yields signiﬁcant improvements irrespective of the application of a

closure at the joint scalar or joint velocity–scalar level. The success of the modiﬁed

Curl’s model in predicting turbulent burning velocities may perhaps be viewed as sur-

prising, and it can be argued that mixing models that enforce locality in composition

space [300, 301] may be better suited to handling combustion in the high-Damk

ohler-

number regime [275]. As noted in Chapter 1, the JPDF approach as implemented

in the context of LES or FDF methods needs to be explored further in the context

of premixed turbulent ﬂames. However, Yilmaz et al. [302] applied a closure at the

joint scalar level to compute a premixed turbulent ﬂame stabilised on a Bunsen

burner with encouraging results. Furthermore, the approach does in principle per-

mit a consistent treatment of pressure terms, provided a higher level of closure is

applied.

Computations of axisymmetric high-Re

turbulent ﬂames with the joint scalar

PDF approach coupled with augmented reduced chemistry showed that the detailed

ﬂame structure can be reproduced with encouraging accuracy – including effects

related to ignition and extinction. However, the reported cases also suggest that

0.00 0.02 0.04

0.06

0.08

r (m)

100

150

k (m

–2

)

Figure 2.45. Radial proﬁles of the kinetic

energy of turbulence



k at x = 0.134 m [283].

Lines and symbols are as in Fig. 2.40.

132 Modelling Methods

a more complete account for the inﬂuence of turbulent transport, including non-

gradient effects, can be expected to further improve model predictions over a wide

range of conditions. Furthermore, the impact of molecular transport on the reaction

rate at the leading edge of the ﬂame can be expected to exert inﬂuence depending

on the nature of the fuel and the Reynolds number of the ﬂow. The inﬂuence of

pressure-related terms was highlighted and the impact of models derived on the

basis of ﬂamelet-related assumptions assessed.

This chapter also highlighted the inﬂuence of boundary conditions and identiﬁed

the closure for the SDR (or time-scale ratio of scalar to mechanical turbulence) as

principal sources of uncertainty. The computations also suggest, by implication,

that scalar dissipation and velocity statistics and scalar ﬂuxes along with detailed

boundary conditions are essential for evaluating and improving the accuracy of the

current models. Hence future progress is inextricably linked to the procurement

of appropriate experimental data sets that should preferably cover a wide range of

Reynolds and Damk

ohler numbers. Such data sets should ideally include information

relating to SDRs, species concentrations, and conditional PDFS for key parameters

such as temperature and pollutants (e.g., CO and NO) exhibiting a range of chemical

time scales.

Acknowledgements

The author wishes to acknowledge the contributions of Tomas H

ulek, Evangelos

aos, Henri Ozarovsky, Magnus Persson, and Philipp Geipel. The encouragement

and ﬁnancial support of Gabriel Roy and the Ofﬁce of Naval Research is gratefully

acknowledged.

Appendix 2.A

The general form of the tensor G

follows directly from the original constant-density

form [264]:

= (α

+ α

)

+ H

ijkl

∂ u

∂x

, (2.173)

where τ

is the time scale of decay of velocity ﬂuctuations (τ



k/˜ε) and the

Reynolds stress anisotropy tensor is deﬁned as









−

. (2.174)

The notation for the contracted tensor product b

= b

and the tensor coefﬁcient

ijkl

is deﬁned as

ijkl

= β

+ β

+γ

+ γ

+γ

+ γ

. (2.175)