Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Наибольшее значение в выражении (XI.

имеет коэффициент /

, обусло-

вленный полярным сжатием Земли, его численное значение 1/1000, в отличпе

от всех последующих коэффициентов, имеющих порядок 10~

и меньше.

Совокупность членов разложения потенциала, вызывающая отклонения

в движении спутника от Кеплерова эллипса, называется возмущающей, или

пертурбационной, функцией. В соответствии с (XI.1) представим возмущающук

функцию в сферических координатах

В — V

/А/

№

-I-

-со п

2 2 {т)

(°

пк

со8 кХ+8пк з1п Рпк

п=2 к=1

(Х1.2)

Часть уравнения (IX.1), не зависящая от долготы, называется зональной

частью потенциала Земли (при к = 0)

Пертурбационная функция от зональной части потенциала Земли имеет вид

В*

}М

_П= 2

(XI.3)

В этом случае гармоники с четным п характеризуют составляющие гра-

витационного поля симметричные относительно экваториальной плоскости.

Так, например, параметр /

характеризует, как будет показано дальше, поляр-

ное сжатие Земли а.

Все гармоники с нечетным п выражают составляющие симметричные

только относительно оси вращения и характеризуют асимметрию северного

и южного полушарий.

При изучении движений искусственных спутников следует учитывать, что

отклонения спутника от Кеплеровой орбиты происходит не только под дейст-

вием гравитационного притяжения Земли, но и под влиянием других факторов,

главными из которых являются: торможение атмосферы, притяжение Луны.

Солнца и радиационное давление Солнца. Хотя возмущающее действие ука-

занных выше факторов на движение спутника по сравнению с действием грави-

тационного притяжения Земли относительно невелико, пренебрегать им в целом

ряде случаев нельзя и поэтому в наблюденное движение необходимо вводить

соответствующие поправки.

Для близких спутников наибольшая поправка обусловлена торможение?:

атмосферы. Главный эффект торможения сказывается на большой полуоси

и эксцентриситете орбиты, которые под действием указанной силы постоянна

уменьшаются. Вычисление этой поправки достаточно сложно, поскольку плот-

ность атмосферы подвержена значительным изменениям во времени.

Возмущающее действие Луны и Солнца будет тем больше, чем больше рас-

стояние спутника от Земли.

310.

Радиационное давление наиболее важно для более удаленных спутников

и тем больше, чем больше отношение площади спутника к его массе. Точная

теория учета всех перечисленных выше факторов пока не разработана. Поправ-

ка, вытекающая из релятивистских уравнений движения, весьма мала и может

не учитываться.

Из сказанного следует, что для определения внешнего потенциала Земли

наиболее целесообразно использовать спутники, параметры движения которых

максимально изменяются под действием возмущений, обусловленных отступле-

ниями фигуры Земли от сферически симметричного тела и практически мало

чувствительны к другим возмущающим факторам.

§ 66. НЕВОЗМУЩЕННОЕ ДВИЖЕНИЕ. ЭЛЕМЕНТЫ ОРБИТЫ

Рассмотрим движение материальной точки Р с массой т вокруг некоторого

вращающегося тела $ с массой М, создающего центральное силовое поле.

В качестве такого тела можно взять шар, плотность которого есть функция

только радиального расстояния (рис. 65).

Возьмем вращающуюся систему пря-

моугольных координат с началом в 8.

Координаты точки Р будут х, у, г.

Дифференциальные уравнения дви-

жения точки Р в выбранной системе

координат имеют вид

Ц2 "Г"

г3

V, -Г

г3

. [Я2 „

где [г = / (М + т)\ / — гравитационная постоянная.

Дифференциальным уравнениям движения можно придать иной вид

<И" ~~ дх ' сИ2

и=

ду '

й^г _ дУ

А& ~ дг '

где V — потенциальная функция тяготения.

Обычно, когда рассматривают невозмущенное движение, под точкой (или

телом) 8 понимают либо Солнце, либо Землю. Соответственно этому за основ-

ную плоскость ху принимается либо плоскость эклиптики, либо плоскость

экватора. При изучении движений искусственных спутников вокруг Земли

оси координат ориентируют в пространстве следующим образом: ось 7, совме-

щают с осью вращения Земли в направлении на север, а плоскость ху с пло-

скостью земного экватора, при этрм ось х направляется в точку весеннего

равноденствия и. Если учитывать, что ось вращения Земли как и точка весен-

него равноденствия меняют свое положение в пространстве, оси координат

относят к некоторой определенной эпохе Т

, при этом ось г направляют к сред-

нему полюсу эпохи Т

, а ось х к средней точке весеннего равноденствия, соот-

ветствующей той же эпохе.

Ориентация плоскости орбиты спутника в пространстве относительно

выбранной неподвижной плоскости экватора ху показана на рис.66. Движение

311.

спутника Р происходит в направлении, указанном стрелкой. Линия пересеч-

ния плоскости орбиты с плоскостью экватора называется линией узлов ЙЙ

Узел, в котором точка (спутник) Р из южного полушария переходит в северно*

называется восходящим узлом (на рис. 66 — точка й), а узел, в котором точк

Р из северного полушария переходит в южное, — нисходящим (точка Й

Угол между плоскостью орбиты и плоскостью экватора называется накло-

ном (или наклонением) орбиты г. Угол об'й между направлением оси х и напр;

влением на восходящий узел называется долготой восходящего узла и обозна-

чается через й. Измеряется она в направлении движения спутника Р.

Интегрируя дифференциальное уравнение движения, определим траекто-

рию спутника

1—{—

е соз

(и -со) " V

•

Это выражение является уравнением конического сечения, фокус которого

находится в точке 8, где р — параметр конического сечения; е — его эксцен-

„ ^Перигей триситет.

Точка орбиты, находящаяся на самом

близком от Земли расстоянии, называется

перигеем, точка орбиты, находящаяся Не

самом далеком от Земли расстоянии, на-

зывается апогеем. Линия, соединяющая

точки перигея и апогея, называется ли-

нией апсид (см. рис. 66).

Полярный угол и, отсчитываемый

от линии узлов 5Й (см. рис. 66) до напра-

вления на спутник, называется аргумен-

том широты, на сфере он измеряется

дугой й(? (рис. 67).

Под величиной со понимается угловое расстояние перигея от восходящего

узла (см. рис. 66).

Обозначим разность и — со через V. Тогда

Экватор

Лпогей

Рис. 66

г=——^ , (XI.5)

1 —(—

соз

где V — угловое расстояние точки Р от перигея — называется истинной ано-

малией.

При е < 1 коническое сечение будет эллипсом и истинная аномалия меня-

ется от 0 до 360°.

Если через а обозначить большую полуось эллипса, то

р = а( 1-е

). (XI.6)

Таким образом, устанавливают шесть параметров Кеплерова эллипса,

которые вполне определяют положение точки Р в пространстве. Эти пара-

метры называются также элементами орбиты. Разобьем их для удобства на две

группы. Первую группу составляют элементы й, со, I, V.

Элементы й и I определяют положение плоскости эллипса относительно

экватора и точки весеннего равноденствия, элемент со определяет ориентацию

линии апсид относительно линии узлов, а истинная аномалия V определяет

положение точки на орбите.

312.

Вторую группу составляют элементы а, е, которые характеризуют размеры

п форму орбиты. Шестым параметром вместо V может служить момент прохо-

ждения точки Р через перигей — т. Прямоугольные координаты точки Р (х, у, г)

связаны с элементами орбиты простыми соотношениями

—

г (соз и соз й — зш и зт й соз г)

у = г (соз и зт й + зт и соз й соз г)

2 = 7

зтизтг

Эти соотношения совместно с равенствами

а (1-е2)

: СО, г

1-)-е соз

(Х1.7)

(XI. 8)

дают искомые координаты точки Р в функции истинной аномалии V и пяти

постоянных: Я, I, со, а, е.

Рис. 67 Рис. 68

Чтобы получить полное решение задачи двух тел, истинную аномалию V

следует выразить в функции времени.

Однако при этом вместо у выгоднее ввести новую переменную, так называе-

мую эксцентрическую аномалию Е (см. рис. 68).

Величины у и Е связаны соотношением

При определении эксцентрической аномалии Е для данного момента вре-

мени I в небесной механике используют трансцендентное уравнение Кеплера

Е — еашЕ=М. (XI. 10)

В (XI.10) принято обозначение

Ш = п{1-т), (XI. 11)

где т — момент прохождения точки Р через перигей и

(XI. 12)

/з •

313.

Величина п связана также простым соотношением с периодом полног'

оборота точки Р, а именно:

360° 2я ,

ут

п =—или п = —. (XI. ^

На этом основании п получило название среднего суточного движения

Величина М — п (I — т) называется средней аномалией. Под средней

аномалией следует понимать угол, на который повернется за отрезок времена

I — т радиус-вектор, вращающийся равномерно, со средней угловой ско-

ростью п.

Иногда вместо т пользуются другим элементом — М

, называемым сред-

ней аномалией для момента или, иначе, средней аномалией в эпоху. Сред-

няя аномалия М

связана с произвольным начальным моментом соотно-

шением

М = ге(*-*

) + М

, (XI.

где М

= п (г

— т). . (XI.15

Таким образом, в качестве шестого элемента орбиты помимо й, г, со, а и е можно

в зависимости от характера решаемых задач использовать т, М

, Е или ь\

однако наиболее частое применение находят величины т и М

Иногда бывает выгодным применять следующую модифицированную

систему эллиптических элементов: Я, I, п, а, е, г.

В этой системе элемент л = Й + со, называемый долготой перигея, есть

угол, измеряемый от точки весеннего равноденствия у до восходящего узла Й

орбиты и далее по орбите до точки перигея. Элемент е, называемый средней

долготой в эпоху, связан с М

соотношением е = я + М

В этой системе элементов средняя долгота спутника Р, обозначаемая

через I, связана со средней аномалией М формулой

= й +

<о

+ М = я +

ДГ.

(XI.16)

Средняя долгота спутника Р может быть определена через величину г как

= е + М-М

. (XI.17)

Величины я, е и / связаны с п

М выражениями

г =

+ п(* + *

). (XI.18)

М = 1- я, (XI. 19)

М = п{1~

)

+ в — я. (XI.20)

Модифицированной системой элементов удобно пользоваться при со близ-

ком к нулю.

§ 67. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ.

ОСКУЛИРУЮЩИЕ ЭЛЕМЕНТЫ

Если в выражении потенциала тяготения V Земли выделить главный член,

соответствующий случаю центрального поля, а всю совокупность по-

следующих членов обозначить через возмущающую функцию К (XI.2),

314.

уравнения возмущенного движения спутника в поле тяготения Земли

будут

АЦ

А1 2

<1*2

(«2

I "V*

—;г-

4-2

гЗ

[Х2

(XI.21)

где X, У, 2 — проекции возмущающего ускорения. Интегрирование системы

(XI.21) в конечном виде оказывается невозможным и поэтому приходится при-

бегать к методу последовательных приближений, пользуясь тем обстоятель-

ством, что возмущающее ускорение весьма мало но сравнению с ускорением,

создаваемым центральным телом (в данном случае — сферически симметрич-

ной Землей). Частный случай 1=7 = 2= 0в уравнениях (XI.21) соответ-

ствует невозмущенному движению. Решение такой системы определяется выра-

жением (XI.7). Отсюда легко получить формулы для производных

Ах

ИГ'

Ау_

А(

Аг

ИТ

Дифференцируя уравнения (XI.7) и учитывая, что Ли — д,V, получим

производные

Ах • Ау __ йг

ПГ^^ ИГ

-У *пг=

= гг~

х + иг (—зт и соз й — соз и зт й соз I)

у = гг

г/ + иг (-8ЩМ8Ш

+ соз и соз й соз I)

2 = гг'

2 + иг соз и зт

)

где

Г —

•

Аг V

1-1 е 81П V

Ау

А(

Ур

УрУр

Г 2

(XI.22)

(XI.23)

(XI.24)

Выражения (XI.7) и (XI.22) можно рассматривать как общее решение

системы дифференциальных уравнений невозмущенного движения.

Найдем решение уравнений возмущенного движения (XI.21) при помощи

уравнений (XI.7) и (XI.22), которые определяют координаты спутника в невоз-

мущенном движении, рассматривая величины Й, I, со, а, е, М

как переменные,

зависящие от времени I.

Эти величины, являющиеся функциями времени, носят название мгновен-

ных элементов; их совокупность определяет мгновенную орбиту спутника.

Таким образом, зная мгновенную орбиту, можно вычислять координаты спут-

ника (точки Р) для любого момента по формулам эллиптического движения.

Функции времени й {I), I ({), со {I), а (I), е ({), М

({), однозначно опреде-

ляемые шестью уравнениями (XI.7) и (XI.22), называются оскулирующими

элементами, а соответствующая им эллиптическая орбита (непрерывно

изменяющая свое положение и форму) — оскулирующей орбитой. Поэтому

315.

оскулирующие элементы можно определить как элементы того невозмущенног

движения, которое имел бы спутник Р, если бы в момент

возмущающе*

ускорение исчезло.

§ 68. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ,

ОПРЕДЕЛЯЮЩИЕ ОСКУЛИРУЮЩИЕ ЭЛЕМЕНТЫ

В предыдущем параграфе было установлено, что для изучения движение

спутника Р можно вместо прямоугольных координат х, у, г определить шесп

оскулирующих элементов: Й, г, со, а, е, М

. Такая замена переменных выгодно

в том отношении, что элементы, остающиеся постоянными в певозмущеннок

движении, в возмущенном движении меняются сравнительно медленно. По-

этому определение элементов й, г, . . . способом последовательных прибли-

жений удобнее, нежели определение ко-

ординат х, у, %.

Прежде чем привести дифференциаль-

ные уравнения, которым удовлетворяют

^ оскулирующие элементы, введем в рассмо-

трение составляющие возмущающего уско-

рения по трем подвижным осям,' неиз-

менно связанным с движущейся точкой Р.

Одну из подвижных осей направим по

радиус-вектору движущейся точки и назо-

вем ее «направлением 8», другую выберем

в плоскости мгновенной орбиты, перпен-

дикулярно к радиус-вектору, и назовем ее «направлением Т», третью ось

направим перпендикулярно к мгновенной орбите и назовем ее «направле-

нием И

». Составляющие возмущающего ускорения по этим осям обозначим

соответственно через 8,Т и IV (рис. 69). Составляющая возмущающего уско-

рения (5? называется радиальной, Т — трансверсальной, И

— бинормальной.

Проведем через точку 5 — начало прямоугольной системы координат —

прямые, параллельные положительным направлениям собственных для точки Р

осей: линии ДО, 8Т и 8№. Тогда положение точки (спутника) Р относительно

осей х, у, г определится тремя эйлеровыми углами: I, й, и.

Направляющие косинусы этих трех направлений относительно неподвиж-

ной системы координат обозначим:

соз (5,

ж)

= а; соз (5,

*/)

= Р; соз (5, г) = у,

соз (Т, х) =

;

соз (Т,

г/)

= Р'; соз (Г, г) = у',

соз (Ж, х) = а"; соз (Ж, р) = Р"; соз (И^, г) = у".

Установим теперь связь между проекциями X, У, Ъ возмущающего ускоре-

ния на неподвижные оси координат х, у, г и проекциями возмущающего ускоре-

ния 8, Т, И

на подвижные оси, связанные с движущейся точкой. Очевидно,

что

8=Ха + У$+2у ч

Т=Ха" + У$" + 2у> . (XI.25)

№ = Ха" + У$" + 2у" |

316.

В свою очередь

Х = 8а + Та' +

\Уа"

У = + + }. (XI.26)

2 = 8у + Ту' + Щ"

Обозначим

5 = У ^ 8, Т = УТ, V? = У^ IV, (XI.27)

и приведем без вывода формулы, устанавливающие зависимость между возму-

щениями в движении спутника и составляющими возмущающего ускорения

^ = Л

шисо8есгИ

, (Х1.28)

М р .

4^-= —со зиШ, (XI.29)

Ир'

йа 2а2вв1пу 2а

^ рц дд^

йЬ р

Ле

а(

=зти8+{сози + соз Е)Т, (Х1.31)

ЙЕО 008 V 77

+ (XI.32)

+ (XI.33)

/ в р

йМ

У~1— е2 / 2ег /1—е2

СОЗ

И е \ р

В дальнейшем для производных йй/й*, йе]д,1, йсо/с^, . . . будем пользо-

ваться также обозначением й, е, со, . . .

Рассматривая полученные уравнения, можно сделать некоторые выводы

о характере вариации элементов орбиты под действием возмущающего ускоре-

ния. Поскольку ускорения 8 и Т лежат в плоскости орбиты, они не могут изме-

нить ориентацию плоскости орбиты в пространстве и, следовательно, не могут

вызвать изменения наклона I или долготы й восходящего узла. Однако они

изменяют а, е, М

и влияют на изменение положения перигея.

Ускорение IV перпендикулярно к плоскости орбиты, и потому не влияет

на изменение большой полуоси орбиты а. Это ускорение вызывает движение

узлов и перигея, а также изменение наклона орбиты I.

В движении узлов и перигея можно выделить члены, равномерно изменя-

ющиеся в течение времени (так называемое вековое движение) и члены, период

которых равен периоду обращения перигея (долгопериодические члены).

Существуют еще и короткопериодические члены, но возмущения от этих чле-

нов имеют период около суток и менее и не влияют на характер векового движе-

ния. Поэтому можно утверждать, что как узлы, так и перигей под влиянием

возмущающего ускорения постоянно смещаются в одном направлении. Линия

узлов имеет обратное движение (т. е. движется в направлении, противополож-

ном движению спутника), а перигей перемещается по орбите навстречу спут-

нику, как схематически показано на рис. 70. Из всех возмущений, наблюдае-

мых в движении спутника, самыми важными являются два вековых движения:

постоянное вращение плоскости орбиты вокруг земной оси (регрессия узлов)

п вращение большой оси орбиты в ее .собственной плоскости (движение перигея).

317.

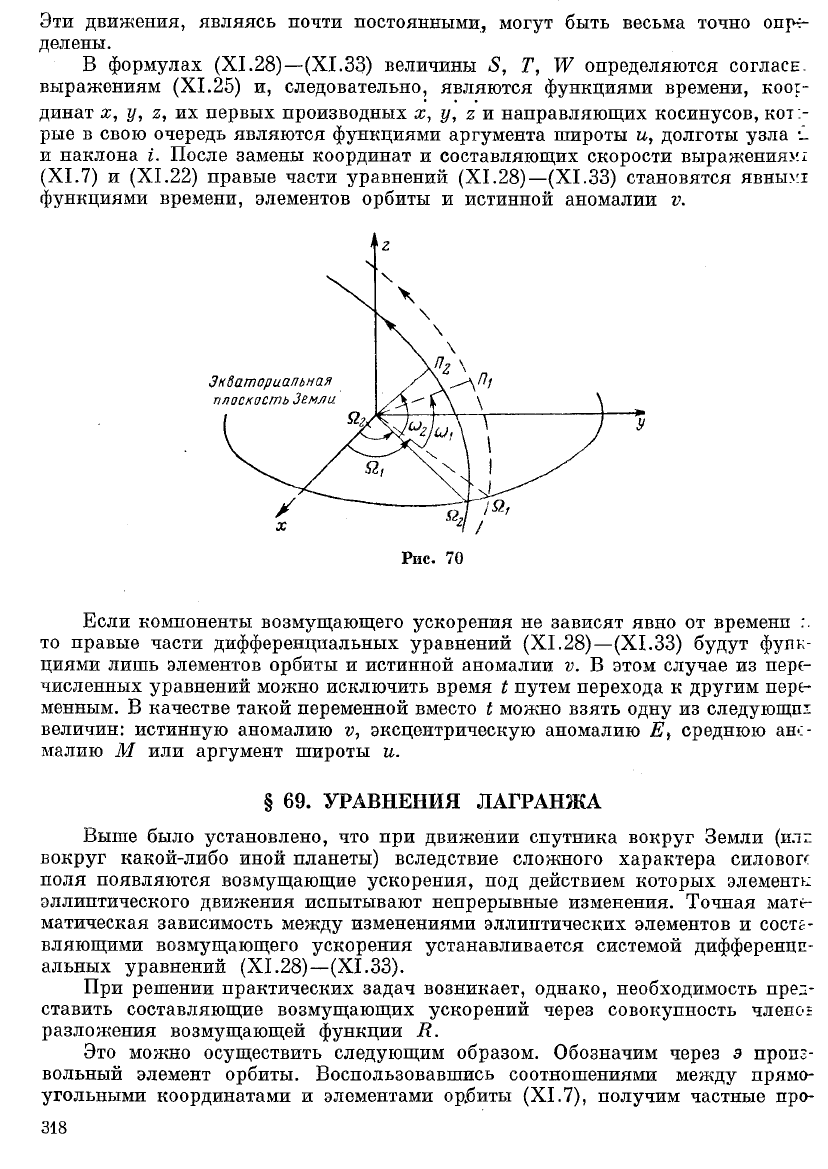
Эти движения, являясь почти постоянными, могут быть весьма точно опре-

делены.

В формулах (XI.28)—(XI.33) величины 5, Т, У/ определяются согласи,

выражениям (XI.25) и, следовательно, являются функциями времени, коор-

динат х, у, их первых производных х, у, г и направляющих косинусов, кот:-

рые в свою очередь являются функциями аргумента широты и, долготы узла

и наклона г. После замены координат и составляющих скорости выражениям!

(XI.7) и (XI.22) правые части уравнений (XI.28)—(XI.33) становятся явным1

функциями времени, элементов орбиты и истинной аномалии V.

Если компоненты возмущающего ускорения не зависят явно от времени :.

то правые части дифференциальных уравнений (XI.28)—(XI.33) будут функ-

циями лишь элементов орбиты и истинной аномалии V. В этом случае из пере-

численных уравнений можно исключить время I путем перехода к другим пере-

менным. В качестве такой переменной вместо I можно взять одну из следующих

величин: истинную аномалию V, эксцентрическую аномалию Е> среднюю ано-

малию М или аргумент широты и.

§ 69. УРАВНЕНИЯ ЛАГРАНЖА

Выше было установлено, что при движении спутника вокруг Земли (ил::

вокруг какой-либо иной планеты) вследствие сложного характера силового

поля появляются возмущающие ускорения, под действием которых элемента

эллиптического движения испытывают непрерывные изменения. Точная мате

матическая зависимость между изменениями эллиптических элементов и соста-

вляющими возмущающего ускорения устанавливается системой дифференци-

альных уравнений (XI.28)—(XI.33).

При решении практических задач возникает, однако, необходимость пред-

ставить составляющие возмущающих ускорений через совокупность члене*

разложения возмущающей функции К.

Это можно осуществить следующим образом. Обозначим через э произ-

вольный элемент орбиты. Воспользовавшись соотношениями между прямо-

угольными координатами и элементами орбиты (XI.7), получим частные про-

318.

дх ди д, ,-г

зводные -д^, и После чего частные производные от возмущающей

функции В по элементам орбиты вычислим по формуле

Ш __дК_дх_.дЯ_ду_ , дП дт.

да дх дв ду да дг да

Так как X, У, 2 зависят от составляющих Т, IV возмущающего ускоре-

5ля (XI.26), то каждое равенство вида (XI.34) представляет собой соотношение

между этими составляющими и частными производными от возмущающей функ-

ции В по элементам возмущенного эллиптического движения. Таким образом,

*ы получаем возможность выразить составляющие возмущающего ускорения

5. Т, IV через производные от возмущающей функции В ив системе дифферен-

циальных уравнений (XI.28)—(XI.33) заменить эти составляющие Т,

соответствующими производными от функции В.

В результате приходим к уравнениям Лагранжа, которые устанавливают

мвпсимость между изменениями элементов орбиты спутника, движущегося

аокруг некоторой планеты, и возмущающей функцией В.

Приведем без вывода уравнения Лагранжа для изменения долготы узла

х перигея

1 дН

(хи5)

110$

1 <?2 8111 I

д1

с? со __ дП со! I дН

й1 па2е де

па

2 ]/"|

2 д1

(XI.36)

Используя уравнения Лагранжа, установим зависимость между возмуще-

жпями, наблюдаемыми при движении спутника и коэффициентами /„, с

пк

1-ь разложения потенциала тяготения в ряд.

§ 70. ТИПЫ ВОЗМУЩЕНИЙ.

ПРЕОБРАЗОВАНИЯ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ

Уравнения Лагранжа, как и уравнения (XI.28)—(XI.33), в конечном виде

не интегрируются. Поэтому для их интегрирования применяют приближенные

численные или аналитические методы.

Рассмотрим типы возмущений, действующих на ИСЗ в полете. Восполь-

зуемся аналитическим подходом. Обозначим через произвольный элемент

орбиты, в качестве независимой переменной интегрирования примем аргумент

шпроты и. Тогда дифференциальные уравнения (XI.28)—(XI.33) можно пред-

ставить в виде

= А

+ 2

(

1к С08 ки

+ В

!к

зт ки),

к=1

где коэффициенты А/ь и В

1к

есть функции элементов орбиты.

319.