Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

или при представлении нечетных зональных гармоник пятью коэффициент

наилучшее решение, по мнению авторов, дает следующие результаты:

= -2,73 ±0,2

= 0,17 ±0,3

= -0,94 ±0,2

= 0,53 ±0,2

= -0,68 ±0,2

За последние годы различными авторами был выполнен целый ряд 01

делений зональных гармоник. Характерными особенностями этих опред.

ний явилось использование орбит с малыми наклонениями (I = 3,5 и 1

большое число используемых ИСЗ (20—27), обеспеченных большим чие~

точных наблюдений, и использование более совершенных теорий движения И

Основные результаты определения зональных гармонических коэффипг -

тов, полученные за последние годы, приведены в табл. 26.

§ 75. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ

СЕКТОРИАЛЬНЫХ И ТЕССЕРАЛЬНЫХ ГАРМОНИК

При определении коэффициентов секториальных и тессеральных гармс:

из анализа возмущений орбит ИСЗ приходится учитывать ошибки не тол

вариаций элементов орбиты спутника, но и координат станций наблюден

По этой причине проблема анализа результатов наблюдений значительно сл

нее, чем при определении зональных гармоник. В частности, при опред'

нии коэффициентов тессеральных и секториальных гармоник нельзя ввод;

в уравнения амплитуды периодических возмущений, как при определе:

коэффициентов зональных гармоник, и приходится анализировать непос*

ственно уклонения наблюденных и вычисленных положений ИСЗ.

При этом используют программы вычислений, базирующиеся на прогр

мах дифференциального уточнения орбит. После получения элементов п{

варительной орбиты остаточные уклонения фактической орбиты от расчет:

представляют как функции поправок к принятым координатам станций еле;

ния, начальным параметрам орбит, коэффициентов разложения гравиташ

ного потенциала Земли в ряд по сферическим функциям и в некоторых случ.

величин, характеризующих сопротивление атмосферы и радиационное г.

ление. Таким образом, возникает большое число определяемых параметр

что приводит к весьма громоздким вычислениям (даже при наличии мош:

ЭВМ) и плохой обусловленности решения.

В 1961 г. Каула предпринял попытку анализа такого рода наблюде;

ИСЗ Авангард 1, выполненных системой Минитрек в течение 385 дней,

были определены поправки в исходные геодезические даты систем Амерг

Южной Африки и Австралии, а также коэффициенты пяти тессеральных г

моник. Однако лишь два из них, а именно при Р

и Р

оказались определ

ными более или менее надежно.

В том же году И. Ия^ак использовал результаты наблюдений спутнп:

1959 а 1 и 1959 т), полученные при помощи камеры Бейкера-Нанна, принпу

положения станций известными и определял только член с Р

, соответствуй

щий сжатию экватора. Соответствующие формулы приведены в §

340.

Таблица

Нормированные значення коэффициентов тессеральиых

секториаиьных гармоник

"„к'

8 .10»

ПК

п и

«5

я 3

я я

от

Ен кН

йн

и 3

СЙ Э

в о

от

1-Н

1—(

са

ан

«Б

и 5

а>

ОГО

то

СУ-1

8«

& й>

осо

нн

1-Н

1-1

ьн

1-1

[3]

1966

[13]

1969

[21]

[25]

1966

1969

2,38

1,94

0,73

0,56

—0,57

0,33

0,85

—0,05

-0,08

0,63

—0,52

—0,26

0,16

—0,05

0,07

—0,05

—0,04

-0,31

-0,04

2,41

1,97

0,89

0,69

—0,53

0,33

0,99

—0,08

—0,05

+0,66

-0,43

—0,27

0,13

-0,10

0,05

0,03

0,00

-0,21

—0,09

2,43

2,00

0,93

0,74

—0,53

0,35

0,99

—0,17

—0,06

0,64

—0,40

—0,29

0,13

—0,08

0,05

0,03

—0,10

-0,26

0,03

2,42

1,99

0,92

0,69

-0,53

0,34

0,98

-0,17

-0,07

0,66

-0,43

—0,25

0,20

-0,08

0,06

0,03

—0,08

-0,26

0,02

2,43

2,02

0,91

0,72

—0,53

0,35

0,98

-0,18

—0,07

0,66

-0,47

-0,32

0,15

-0,09

0,07

0,02

-0,11

-0,30

0,04

2,42

2,02

0,92

0,71

-0,53

0,35

0,97

-0,18

-0,07

0,66

-0,47

-0,31

0,17

-0,09

0,07

0,02

—0,10

-0,30

0,03

2,44

2,00

0,91

0,69

-0,54

0,34

0,90

—0,18

-0,04

0,66

-0,46

—0,28

0,12

-0,07

0,11

—0,03

-0,10

—0,34

—0,05

—1,35

0,27

—0,54

1,62

-0,47

0,66

-0,19

0,23

—0,10

—0,23

0,01

0,06

-0,59

—0,03

—0,37

0,03

-0,52

-0,46

-0,16

-1,36

0,26

-0,63

1,43

-0,49

0,71

-0,15

0,34

-0,10

-0,35

-0,09

0,08

-0,60

0,04

-0,35

0,04

-0,40

—0,52

-0,07

-1,37

0,24

—0,61

1,40

-0,44

0,68

-0,21

0,30

-0,10

-0,31

-0,25

0,04

—0,67

—0,03

—0,35

-0,01

—0,45

-0,53

-0,24

-1,38

0,24

—0,62

1,46

-0,46

0,68

-0,21

0,31

—0,09

—0,31

—0,18

—0,04

-0,67

0,01

—0,36

0,02

—0,45

-0,56

-0,25

—1,39

0,25

-0,62

1,42

-0,44

0,66

—0,22

0,31

—0,08

—0,32

-0,28

0,03

—0,68

-0,02

—0,37

-0,03

-0,46

—0,50

-0,22

-1,39

0,25

-0,63

1,42

-0,46

0,67

-0,22

0,32

-0,08

-0,31

-0,25

0,03

—0,69

0,01

-0,38

—0,01

—0,46

-0,51

-0,23

-1,36

0,21

—0,70

1,39

—0,47

0,67

-0,20

0,34

—0,07

-0,32

—0,20

0,01

—0,58

0,04

-0,35

0,02

—0,47

—0,46

-0,24

Использование двух спутников позволяло получить два независимых определ-

ния постоянных. Фазовый угол тригонометрических членов (XI.61) и (XI.61

имеет незначительное суточное изменение, поэтому для вычисления постоян-

ных а' и 1

желательно использовать длинные интервалы времени. Однако дан.-

в случае таких относительно высоких спутников, как 1959 а 1 и 1959 т), ок.

залось невозможным с достаточной точностью в течение слишком длинно:

интервала времени представить эффект торможения в атмосфере в виде прс

стых полиномиальных выражений. Поэтому пришлось ограничиться 20-днег

ными интервалами. Все орбитальные элементы были представлены в вил

полиномов первой (г и е), второй (со и Й) и третьей степеней (средняя ан>

малия М).

В программу вычислений включались полученные эмпирическим нуте;

прямые и непрямые эффекты торможения в атмосфере, радиационного давления

вековые и долгопериодические возмущения, обусловленные четными и нечет-

ными зональными гармониками в гравитационном потенциале Земли, лунн> -

солнечные возмущения и аналитические выражения для короткоперподическп:

возмущений первого порядка, обусловленных сжатием Земли.

Вычисление постоянных а' и 1

, входящих в уравнения для бсо, 60, 6

и бМ, повторялось до тех пор, пока новые значения не совпали со старыми в пре-

делах ошибок их определения.

Наиболее надежные модели тессеральных гармонических коэффициентов

были получены в период 1970—1973 гг. в (СЕМ I—VI) и (Стандартны,

Земли I—III). Названные модели содержат полные ряды коэффициенто:

до 12—16 порядков, а также ряд резонансных коэффициентов до п = 22

В определения включено большое количество (порядка 300 ООО—500 000

различных наблюдений 20—27 ИСЗ с пунктов Мировой сети. При определенпг

моделей ОЕМ II, IV и VI, а также Стандартной Земли II и III помимо спут-

никовых наблюдений использовались наземные гравиметрические данные в вид

средних аномалий по трапециям 5 X 5°, охватывающие около 70% поверхност;

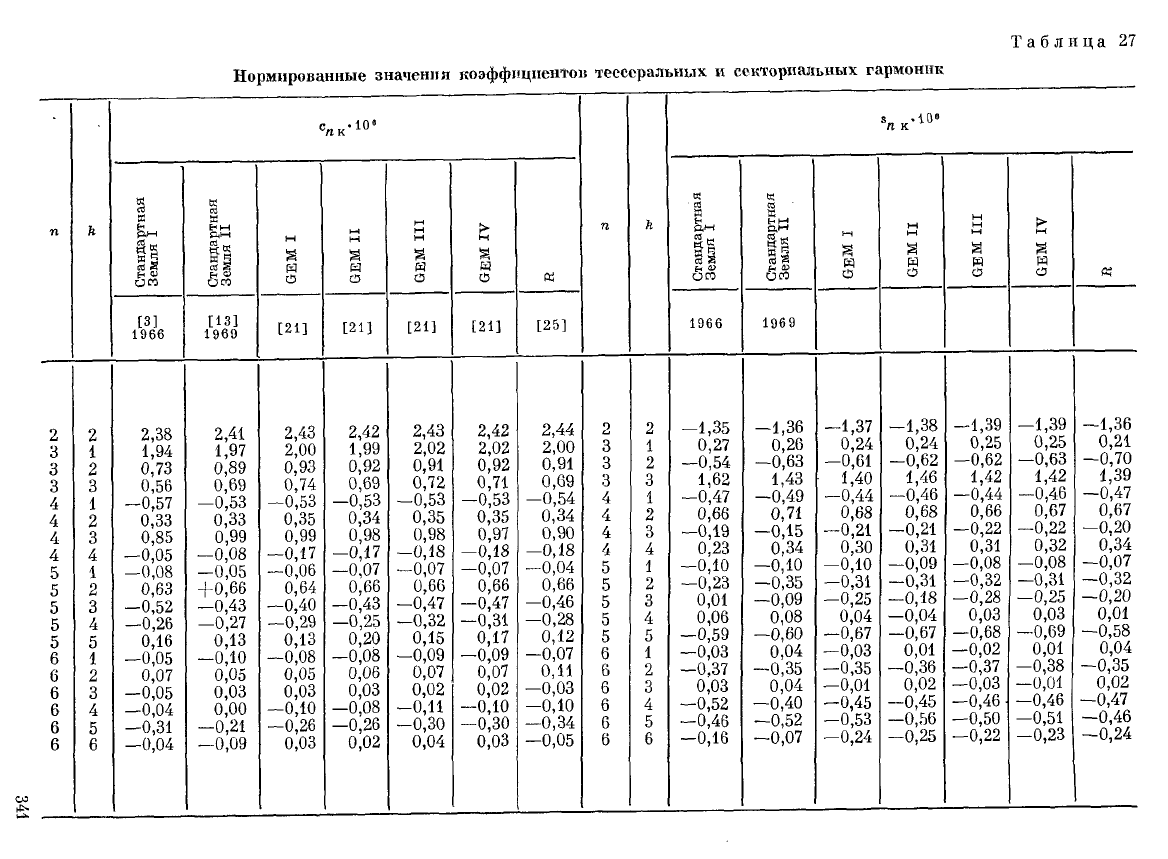
земного шара. Результаты указанных определений коэффициентов тессераль-

ных гармоник (ограничиваясь п = 6) приведены в табл. 27.

§ 76. СВЯЗЬ МЕЖДУ ДИНАМИЧЕСКИМИ ПАРАМЕТРАМИ

И ГЕОМЕТРИЧЕСКИМИ, ХАРАКТЕРИЗУЮЩИМИ

ФИГУРУ ЗЕМЛИ

Коэффициенты /М, с

пк

и з

пк

принято называть динамическими. Эти коэф-

фициенты позволяют однозначно определить такие геометрические параметра

характеризующие фигуру Земли, как значения полуосей общего земного эл-

липсоида, полярное и экваториальное сжатие, параметры, характеризуют^

асимметрию северного и южного полушарий, и отклонения поверхности кь,-

зигеоида от общего земного эллипсоида. При помощи динамических коэффи-

циентов определяются также координаты центра масс Земли и направление гляч-

ных осей инерции.

Введем в качестве фигуры относимости трехосный эллипсоид с полуосям;

а,

и с. Полярное а и экваториальное а' сжатия эллипсоида будут определяться,

как

а — с , а — Ь

342.

Эти параметры связаны с разностями С—А

и В—А главных моментов

инерции эллипсоида

/ (С - АЛ = ^ (2а - а

) - ^ (1 -1 а ) , ' (XII.23)

= (ХН.24)

В свою очередь разности главных моментов инерции эллипсоида на осно-

вании формул (IV.28), (IV.30) и (IV.33) можно связать с динамическими коэф-

фициентами /

и с

= (XII.25)

(

ХП

)

а при помощи формул (XII.23) и (XII.25) установить зависимость между /

и а

Т * /о о\ со2

з / 9 \

(2а-а-) —^ (!--<*)•

Последний член справа с учетом (V.27) и (У.22) можно представить

а)- V ' '

V 7 }

С точностью до малых величин второго порядка получим

шз а / 9 \ ?/, 2 3 \

ттлг ( т

)

т( у

а —

2"^)

Решая это уравнение последовательными приближениями, можно выра-

зить полярное сжатие а через коэффициент /

. С точностью до малых величии

первого порядка

а = ~/2 + у. ""• (XII.28)

Выразим экваториальное сжатие а' через коэффициент с

. На основании

(XII.24) и (XII.26)

1 ,. со-а 4 , /ллтт оп\

= ]м~Ж

- (XII.29)

а2

Для определения величины ]М!а

воспользуемся формулой {Ч .21)

= + а). (ХП.ЗО)

Член (<о

а)/(Щ)/а

в выражении (XII.29) можно представить в виде

со

а о)2а й)2о

/ЛГ

а2

Т.(1-«) + -|

шВа

(

—Т

) V, [!-«+-§-г (1-уа)]

343.

Таким образом, (со

а)/(/М/а

) — д = ад — 3/2д

, т. е. различие между

(со

а)/(/М/а

) и д является величиной второго порядка.

В формуле же (XII.29) из-за наличия множителя а' замена

(со

а)/({М/а

)

на г

вызовет пренебрегаемо малую ошибку четвертого порядка, следовательно,

или

Отсюда получаем

1,4,

- Ж«

6с

= а'—^а'д.

1-у

«Г

или, ограничиваясь малыми величинами второго порядка,

а" = 6с

. (XII.31)

Разность (а—Ь) максимального и минимального радиус-вектора эквато-

риального сечения трехосного эллипсоида определяется через коэффициент с

а — 6 = аа' = 6ас

. (XII. 32)

Для получения разложения высоты квазигеоида в ряд по сферическим

функциям воспользуемся соотношением (VI.21). При этом для возмущающего

потенциала используем разложение (VI.4*), положив М = М

и приняв

начало координат совмещенным с центром массы Земли. Тогда для высоты

квазигеоида будем иметь

оо п

2 (?)"

{Спк со8кК+8пк 8[п к1) Рпк (е)

и=2 к=0

Полагая а = р = В, у = /М/В

, получим

со п

(с

пк

соз кХ + з

пк

зт кХ)

(6) = -йс

(соз 8) +

со п

+ Вс

(соз 9) + ... + В 2 2 (с

пк

соз кХ + $

п/г

зт кХ) Р

пк

(6).

п= 2 й=1

Асимметрия северного и южного полушарий Земли характеризуется не-

четными гармониками в разложении Наиболее крупная волна квазигеоида,

вызывающая асимметрию полушарий, определяется зональной гармоникой

третьей степени в разложении Х>

= с

за

ВР

(соз 9).

Определим эту асимметрию:

при 8 = 0, соз 8 = + 1, Р

(соз 8) = + 1, 1

= + с

В,

при 8 = 180°, соз 8 = —1, Р

(соз 8) = —1, = —

зо Я.

Следовательно, квазигеоид у северного полюса будет приподнят на вели-

чину с

В и настолько же опущен у южного полюса. Асимметрия полушарий

составит при этом величину 2с

В метров.

344.

Высоты квазигеоида (геоида) являются наиболее наглядной характеристикой

возмущающего потенциала Земли. В настоящее время в результате целого

ряда выполненных различными авторами исследований амплитуды многих

наиболее значительных поднятий и опусканий геоида (квазигеоида) уверенно

-.180460°-Н0Ч20Ч00°-80°-60° -40° -20° О° 20° 60° 80° 100° 120° М° 160° 180

Рис. 73

выявлены и служат удобной для решения многих задач характеристикой гео-

потенциала.

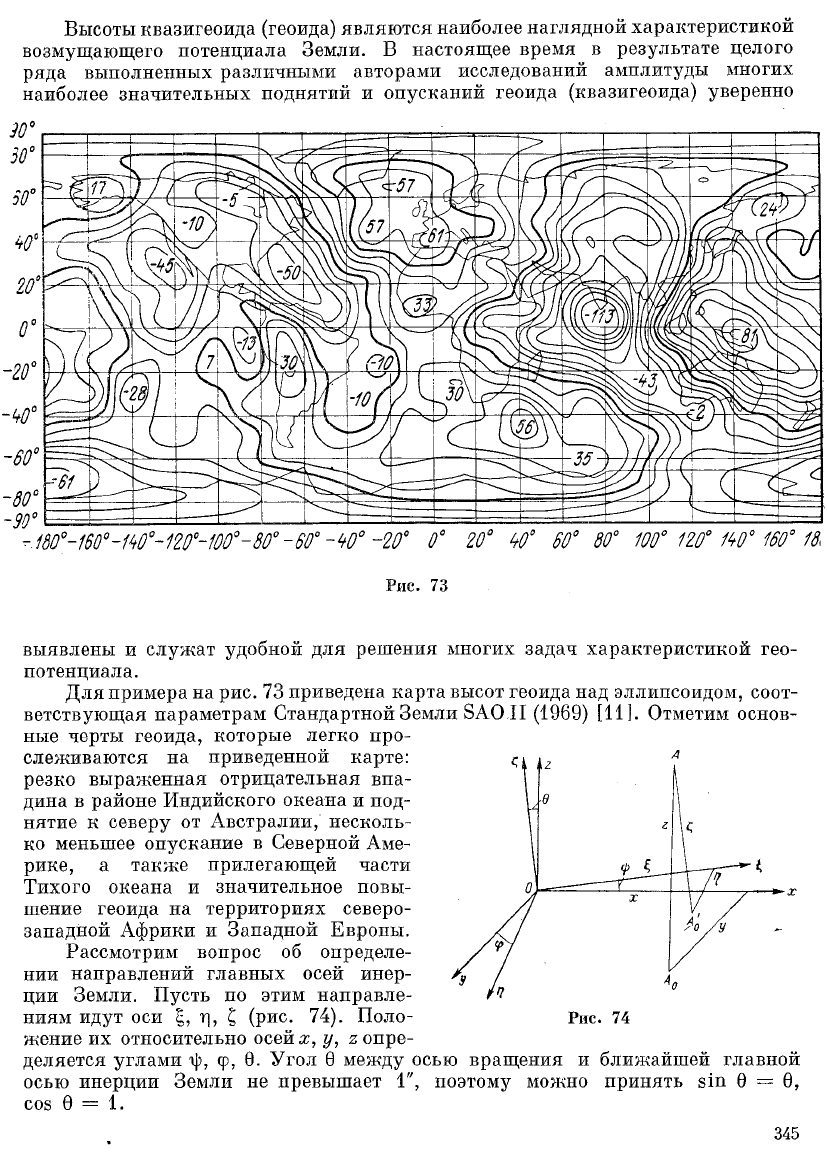
Для примера на рис. 73 приведена карта высот геоида над эллипсоидом, соот-

ветствующая параметрам Стандартной Земли ЗАО II (1969) [11]. Отметим основ-

ные черты геоида, которые легко про-

слеживаются на приведенной карте:

резко выраженная отрицательная впа-

дина в районе Индийского океана и под-

нятие к северу от Австралии, несколь-

ко меньшее опускание в Северной Аме-

рике, а также прилегающей части

Тихого океана и значительное повы-

шение геоида на территориях северо-

западной Африки и Западной Европы.

Рассмотрим вопрос об определе-

нии направлений главных осей инер-

ции Земли. Пусть по этим направле-

ниям идут оси г], % (рис. 74). Поло-

жение их относительно осей х, у, г опре-

деляется углами -ф, ф, 8. Угол 0 между осью вращения и ближайшей главной

осью инерции Земли не превышает 1", поэтому можно принять зт 0 = 9,

соз 0 = 1.

Рис. 74

345.

В этом случае

\—х соз

(г|)

ф)

зт +

ср)

зт ф,

т)

= — х зт

(ф

ф)

+ у

соз (г|з

ф)

соз

ф,

^ = Х&

8111 я[з

— г/0 С08 + 2.

Составим выражения для произведений инерции и ] ^г,.;

и приравняем их нулю, так как оси т), I, — главные оси инерции Земг:

В полученные уравнения введем моменты инерции Земли А, В и С относительу

координатных осей х, у, г, а также произведения инерции относительно тех :-:

осей. Используя зависимости § 21, установленные между этими величинами

коэффициентами с

, с

, $

, с

и 8

, после некоторых преобразований пол

чим выражения для углов, определяющих направления главных осей инернг:

Земли

2(г|>+

) = -^., 0 =

(С21)2+(521)2

. (ХН.О

22 С 2 О

Сравнивая значения высот квазигеоида (геоида), полученные по резуль-

татам спутниковых наблюдений со значениями тех же высот, определенные

астрономо-геодезическим методом ^дг, можно получить размеры общего зе?

ного эллипсоида.

Систематическая часть разности —определенная по возможно бог:

шему числу станций, характеризует отличие в значениях больших полуоск

референц-эллипсоида и общего земного эллипсоида. Таким образом, если с::

тать сжатие а общего земного эллипсоида известным, то поправка Да к бо.~"

шой полуоси может быть найдена из соотношения (^аг —?

)ср

•

Недостаток данного метода определения большой полуоси по отдельнь.

станциям состоит в том, что при этом не учитываются высокочастотные ВОЛЕ:

геоида. Эту трудность можно частично преодолеть, согласовывая с результатам^

полученными спутниковым методом, не отдельные значения высот, а полнк

карты высот геоида, составленные астрономо-геодезическим методом.

§ 77. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОБЩЕГО

ЗЕМНОГО ЭЛЛИПСОИДА И КООРДИНАТ ЦЕНТРА

МАСС ЗЕМЛИ

Совместное использование астрономо-геодезических составляющих укл

нений отвеса "ЧАГ или высот квазигеоида ^

Г, полученных методом и.:

ропомического или астрономо-гравиметрического нивелирования, и «плане

тарных» характеристик гравитационного поля Земли ц или полученш:

по гравиметрическим и спутниковым данным, позволяет определять параметр

общего земного эллипсоида и элементы его внешней или внутренней ориенг

ровки в теле Земли. В настоящее время сжатие общего земного эллипсои.

получено с высокой степенью точности по результатам наблюдений ИСЗ. Поэт

задачу определения параметров и ориентировки общего земного эллипсои

можно свести к определению его большой полуоси и координат центра м^

Земли.

В 1956 г. И. Д. Жонголович [1] подробно рассмотрел теорию мет<

позволяющего определить параметры и элементы ориентировки общего земн-

эллипсоида. Сущность этого метода состоит в следующем. Сначала

346.

гравиметрическим данным определяют сжатие общего земного эллипсоида и

планетарные характеристики гравитационного поля Земли (составляющие укло-

нений отвеса | и г), высота квазигеоида Затем, считая полученное сжатие

общего земного эллипсоида окончательным, по астрономо-геодезическим со-

ставляющим уклонений отвесных линий в плоскостях меридиана |АГ

первого

вертикала ЛАГ или по высотам квазигеоида ^АГ И планетарным характеристи-

кам 5, г), \ определяют из решения системы уравнений градусных измерений

большую полуось общего земного эллипсоида и элементы внешней или внут-

ренней ориентировки референц-эллипсоидов относительно центра масс Земли.

Рассмотрим этот метод. Если обработка астрономо-геодезических изме-

рений на референц-эллипсоиде выполнена по методу развертывания и для не-

которого начального пункта к, кроме составляющих астромоно-геодезических

и планетарных уклонений отвеса известны составляющие абсолютного укло-

нения отвесной линии с,

, г]

, которые получаются не только на основании

данных о внешнем гравитационном поле Земли (как планетарные), но и на

основании детальной гравиметрической съемки в районе данного пункта к,

то для каждого астрономо-геодезического пункта исследуемой территории можно

составить градусные уравнения

+ [ёАГ-^ + А !*)+Ра

(ЛАГ

—ЛА) +

+ р

6з

+ +

Рв Ла\

= V,

+ [ЛАГ —

Ц1

Я1

— + (ЛАГ — ЛЙ) + + =и?

{

где — длина геодезической линии от начального пункта к до текущего г;

— геодезический азимут.

Величины в квадратных скобках являются свободными членами, а вели-

чины и Ю; представляют собой остаточные погрешности этих уравнений.

Вся система уравнений решается относительно неизвестного ба/а по способу

наименьших квадратов при условии 2 (

у2

+ м

) —

- Если данных для

надежного вывода абсолютных уклонений отвеса |

и т]

даже для одного ка-

кого-либо пункта к недостаточно и имеются лишь планетарные значения §

и т] для всех пунктов съемки, то кроме неизвестной поправки в большую полуось

6а следует считать неизвестными также величины (^АГ —1

)> (ЛАГ —Л

)

и 6Т^ и использовать следующие уравнения:

Рх (!АГ - !*) +

Рг

(ЛАГ - Л*) + Р4 йТ

+ Рь^- +

+ [|АГ — \ —Рз

й«1

Рв _

Ях

(ЙГ- 1

) +

Я*

(ЛАГ-Л,) + Я,йТ

+ +

+ [л^

—

ЛI

Яз

+ Я

^а] =

Рассмотрим несколько подробнее случай обработки астрономо-геодези-

ческих измерений по методу проектирования. Пусть имеются две геодезические

системы координат: референц-система, координаты в которой отсчитываются

относительно референц-эллипсоида (большая полуось а, сжатие а) и абсолютная

система, координаты в которой отсчитываются относительно общего земного

эллипсоида (большая полуось а, сжатие а).

Получим соотношения между двумя системами геодезических координат

для некоторой произвольной точки Р земной поверхности.

В системе прямоугольных координат х, у, 2, за начало которой принят

центр референц-эллипсоида, направим ось 2 по направлению полярной осг

референц-эллипсоида, оси х и у расположим в плоскости экватора.

В референц-системе прямоугольные кординаты точки Р будут х, у, г.

а геодезические — Н (высота), В (широта) и Ь (долгота). Связь между прямоуголь-

ными и геодезическими координатами определяется соотношениями

х = ^+ Н)соиВ созЬ, |

У — Н) соз В 5111Ь, , (XII.34

2 = [ЛГ(1— е

) + #]зтЯ ]

где

VI— «

81П2Д

радиус кривизны первого вертикала;

V о,'

—б

е =

эксцентриситет меридиана.

Пусть имеется также и другая — абсолютная — система как прямоуголь-

ных координат х, у, 2, так и геодезических Н, В, Ь той же точки Р Земли. При

этом прямоугольные оси О, X, У, 2 абсолютной системы расположены парал-

лельно предыдущей, и начало прежней системы имеет в новой системе коор-

динаты х

, у

, 2

, так что

х = х + х

Уо,

2 =

+ 2

. (XII.351

Соотношения между абсолютными прямоугольными и геодезическими ко-

ординатами выражаются формулами аналогичными (XII.34). Напишем теперь

соотношения между двумя системами геодезических координат произвольной

точки Р. Для этого следует в выражение (XII.35) лишь поставить указанные

соотношения для прямоугольных координат точки Р. Получим

(ТУ + Н) соз В соз Ь = (И + Н) соз В соз Ь + х

(В +~Н) со

В зт 1 = (А

+ Н) соз ВзтЬ + у

[ТУ (1 —ё

) + Н] зт В = (1 -

)

+ Н] зт В +

(ХИ.31

При известных значениях, а, е, а, е, х

, у

, 2

, характеризующих размеры,

форму и взаимное расположение эллипсоидов, можно с помощью этих форму."

по заданным значениям геодезических координат Н, В, 2 некоторой точки /

рассчитать координаты Н, В, Ь этой точки, и наоборот. Однако это не очень-

удобно для вычислений. Преобразуем формулы (XII.§6) последовательнс-

умножив их сначала на соз В соз Ь, соз В зт Ь, зт В, затем на зт В соз Ь.

348.

вп В зш Ь,—соз В и, наконец, на зт Ь, соз В, О. В результате после не-

яачительных преобразований получим точные формулы преобразования

геодезических координат

(.V+Н)

соз (В — В) — 2

соз

В соз В зт

ь—Ь

— е-М зт В зт В

= N + Н—зт

В — {х

соз В соз Ь + у

соз В зт Ь + 2

зт В)

(Х + Н)

зт (В — В) + 2

соз

В зт В зт

— е

7Узт5 соз 5

(XII.37)

= — зт В соз В — (х

зт В

соз

Ь + у

зт В зт Ь — 2

соз

В)

(Л

+ И) соз В зт (Ь

—

Ь) — — х

зт Ь + у

соз Ь

Упростим полученные формулы, сохраняя малые величины шестого по-

рядка {

% «1:3 ООО ООО). Под малой величиной первого порядка будем по-

нимать величину е

= 1 : 12, близкую к эксцентриситету меридианов. В соот-

ветствии с этим будем пренебрегать произведениями величин

Да

Дв« =

—е

, В —В, Ь

а также произведениями этих величин на Н/а и Н/а. Для этого достаточно при

величине а, близкой к 6000 км, полагать, что значение каждой из величин

, у

о,

, Да не превосходит 1 км, значения Н и Н не превосходят 6 км, а об-

ратная величина сжатия отличается от 300 не более чем на 10 единиц.

Введем вместо эксцентриситетов е и е сжатия а и а, связанные соотноше-

ниями е

= 2а—а

, е

= 2а—а

, и обозначим Да = а—а.

Если произвести с указанной точностью все необходимые преобразования

выражений (XII.37), получим приближенные формулы

Н__Н__ Да

а а а

а зт"

(В-

где

зт

В —^ зт

2В

В) + Да (зп

4- (Ш.

соз

В соз Ь + соз В зт Ь + зт В )

я а а

В)" = зт 2В + Да

— а + 2а зт

В) зт 2 В

— 81П В СОЗ + — 31П В зт Ь — — СОЗ В )

а а а /

(Ь — Ь)" зт 1"

соз

-2- 31П Л/ -|—СОЗ Е/

а а

У О

1 —е2

, (XII.38)

(1—е2

81П2

В)

3/г

Три величины ж

, у

, г

, определяющие сдвиг центра референц-эллипсоида

по отношению к центру общего земного эллипсоида, можно заменить тремя

геодезическими координатами Н

, В

, Ь

произвольной начальной точки к

349.