Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

то неучтенная часть высоты квазигеоида I, будет определяться формулой

Л 2Я

о о

в которой 8 (ф) — непрерывная на отрезке 0 ф я кусочно-гладкая фуь; -

ция, равная постоянной (ф

) при 0 с ф

==5

и совпадающая с функцз?-*

Стокса при ф

ф ^ я. Если функцию $ (ф) разложить по полиномам .".—

жандра, обозначив коэффициент п-ой степени этого разложения через [(2г. -

+ 1)/2] @

, то неучтенную часть высоты квазигеоида I, можно представг~«

в виде

со

Этот ряд сходится быстрее аналогичного рада (XIII.9).

Рассмотрим кратко способ М. С. Молоденского.

Можно считать, что после выполнения интегрирования в пределах облает

радиуса ф

(XIII.2) величина А^ определяется формулой

Я 2Я

А ь = Л {ё~

У)р

8 (ф) аш

ф йг|>

Л А,

о о

в которой интегрирование ведется по всей сфере, функция 8 (ф) — разрывна

равная нулю при ф <ф

и равная 8 (ф) при ф - ф

. Введем вместо функпп

<5 (ф) ее приближенное значение 8

(ф) в виде разложения функции Стог:«

8 (ф) по полиномам Лежандра до степени т. Эту функцию 8

(ф) Молоденскг!

определяет из сл ующих двух условий:

1) (Ф) является многочленом степени т от сов ф;

2) коэффициенты этого многочлена определяются при условии

^ [5 (ф) — 8

(я|;)]

зт ф йф ЗА = тт.

Фо

Цель последующих преобразований СОСТОИТ В ТОМ, чтобы вновь образован-

ный ряд сходился значительно быстрее, чем первоначальный ряд Стокса, в итч:-

вале от ф

до я (и, конечно, медленнее в интервале от 0 до ф

, что, одна:- .

в данном случае не существенно). Тогда формуле Стокса можно придать ЕЕ I

вид. Интегрирование должно распространяться только на близлежащие к псс-~.г-

дуемому пункту области; наоборот, дальние зоны проще всего учитывать ан.-

литически — разложением их влияния по сферическим функциям. Если ог: •-

ничить область изменения я); интервалом от ф

до я, то подходящим выбо: :»

угла ф

можно в этом интервале получить для функции Стокса достаток:

быстро сходящийся ряд, в котором практически можно ограничиться несколь-

кими первыми членами.

Следовательно, непосредственное интегрирование следует выполнять лг:*

в области от 0 до ф

. Действие аномалий в области от г|)

до я достаточно точзх

при этом учитывается первыми членами разложения ряда сферических фун1-

360.

ций. В этом состоит основная идея преобразования формулы Стокса. Если

вместо функции 5 (Ф) использовать функцию 8

(гр), то формулу Стокса (XIII.2)

следует представить в виде суммы трех членов

•фо 2Я

Бо

+ +

& = $ $ -

У)р

(гр) - 8

(г|з)]

зт

ар

# а А +

о о

Я 2Я

о о

Я 2Я

+ ^

8т

81П

^ ^

АА

Фо

Первое условие, поставленное Молоденским, позволяет точно предста-

вить Асуммой сферических функций до степени т включительно. Второе

условие при соответствующем выборе ф

и т — член сделать меньше любой

наперед заданной величины с тем, чтобы можно было им пренебречь. В этом

случае

Фо 2Я

о о

Я 2Я

+ 4^" И &ДО) йпфЛМЛ. (Х1П.Ю)

о о

Разложив функцию 8

по полиномам Лежандра и представив аномалию

силы тяжести через ограниченную сумму сферических функций в соответствии

с (XIII.4), М. С. Молоденский получил выражение для Д^ в виде

п= 2

Тогда окончательно

Фо 2Я т

1= | 5 (ё - У)г [3

ДО)

- ДО)] зт ^ Лр й/1 + А- 2 (З

) д

(9, X).

О 0 п= 2

(XIII.11)

Числовые значения коэффициентов К

) при т = 6 и т — 8 приведены

в табл. 32—33.

Таблица 32

(8.)

г, км

Кг (8.)

К,

(3.)

«4 (8.) к» (8.)

к. (8„)

1274

2548

3823

+ 1,716

+ 1,551

+1,425

+0,720

+0,570

+0,467

+0,393

+0,261

+0,182

+0,233

4-0,122

+0,068

+0,140

+0,052

+0,020

361.

Таблица

)

г, км

Кг (За)

(За) к

(За)

К, (3,) К

(За)

. К

(За)

К а (5,

1274

2548

3823

+1,748

+1,610

+1,503

+0,751

+0,624

+0,532

+0,422

+0,308

+0,234

+0,261

+0,162

+0,106

+0,167

+0,084

+0,045

+0,107

+0,041

+0,017

+0,067

+0,017

+0,005

Итак, формула (XIII.9) Еремеева и Юркиной, аналогичная формула Оста-

и формула (XIII.11) Молоденского являются обобщением формулы Стоки

и ряда Стокса. Обе формулы при т —>- оо совпадают с решением Стокса. Хот*

метод Молоденского для учета дальних зон дает большую точность, чем мет .

Еремеева и Юркиной, он не получил применения из-за того, что при переход

к нему необходимо заново повторить большой объем вычислений, уже выпол-

ненных по интегральным формулам. В практике нашел применение мет. :

Еремеева и Юркиной, в котором не требуется повторять прежних вычислении,

и метод Остача, дающий точность, близкую к методу Молоденского.

§ 79. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ВЛИЯНИЕ АНОМАЛИЙ

В ДАЛЬНИХ ЗОНАХ

Для оценки среднего квадратического влияния аномалий дальних зс

будем исходить из преобразованной формулы Стокса (XIII.9). Среднее квадр.

тическое значение А^ влияния аномалий в области, расположенной за окру? -

ностью со сферическим радиусом "ф

, на высоту квазигеоида равно

где А^ — второй член формулы (XIII.9).

Подставляя значение А^, получим

_Й!_ГГ

со

<?пёпр, я')

ЙСО.

На основании свойства ортогональности сферических функций члень;

вида

т!^-<?*<?'И а/)йа>

со

будут равны нулю и

П-2 со

где — порядковая дисперсия аномалий силы тяжести. На основании иссл

дований найдено значение этой величины, равное примерно 120/га мгл

Збй'

Введем в рассмотрение величину §

, определяемую равенством

^ = (XIII.12)

со

Эту величину выразим через коэффициенты А

пк

и В

пк

разложения анома-

лии силы тяжести

пк

созкк Р

пк

(О')+ 2 В

пк

зткХ'Р

пк

(&')

к=1 , к=1

(О со

Преобразуем это выражение. Найдем

= (А

по

)

Р%

(соз 6')

йсо

+ 2 (А

пк

у ЭД соз

кЪ'

[Р

пк

(0')]

Лв +

со со со

к-1

^ ^

со

^Р

(СО3 0')Й©=-2^

<2со.

Поскольку

(С08

ИЛ

2л (п+к) !

2я-)-1 (га—/с) ! '

получим

Следовательно, среднее квадратическое значение сферической функции

?г-й степени в разложении аномалий силы тяжести в соответствии с (XIII.12)

можно выразить через коэффициенты А

пк

и В

пк

й-

(А,

)

Таким образом, с учетом (XIII.12) получим

4у2 ^ Чпёп

где

А =

(XIII.14)

является средним квадратическим значением члена п-ш степени в разложении Д^

в ряд по сферическим функциям. Формулу для вычисления можно написать

иначе.

363.

Известно, что при ф

= 0 формула (XIII.9) превращается в ряд сфег

ских функций, для которого

Уп

•

Выше было показано (VIII.27), что сферическая функция Т

(0, А

степени в разложении возмущающего потенциала связана со сферической

цией д

(0, X) той же степени в разложении аномалий силы тяжести соотн-

нием

Тп{

Используя выражение (VI. 21), найдем, что сферическую функцию 1,

(/г

п-й степени в разложении высоты квазигеоида можно представить в виде

с„(в,

Таким образом, выразив при помощи этого соотношения §

через пс

чим

(д—1) у у

а подставив это значение в (XIII.14), получим более удобную формулу ~

вычисления среднеквадратического влияния дальних зон на высоту кв.

геоида

Чп = ^<2пйп. (XIII.

Для определения среднего квадратического влияния дальних зон на уб-

иение отвеса применяется формула (М. С. Молоденский, В. Ф. Еремс

И. М. Юркина, 1960 г.)

СО

(XIII

71=2

Выполним преобразования, аналогичные тем, которые были сделаны в г

ражении (XIII.14). В данном случае можно выразить через среднее квад

тическое значение члена п степени разложения в ряд уклонения отвеса.

Если ф

= 0, то (?„ = 2/(п — 1), АI = Аг] = т] и среднее квадратичен

значение уклонения отвеса на Земле определится по формуле

оо

|2 I

V >

Ь 1

Л (и —1)2

71=2

Отсюда среднеквадратическое значение члена п-й степени разложен*,

в ряд уклонения отвеса будет

ёп+Пп— („_

1)2

8п-

Следовательно,

2 1)"

о /^о

364.

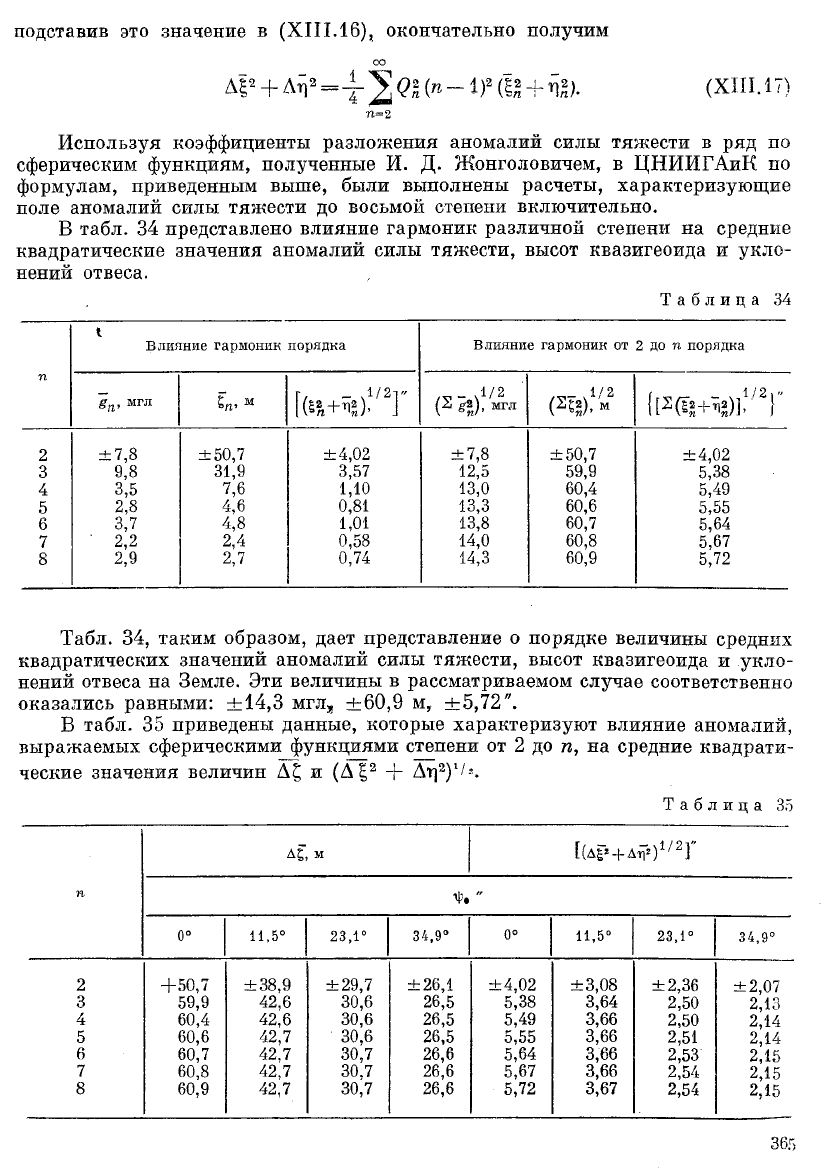
подставив это значение в (XIII.16), окончательно получим

со

А!

+ Л^

= -12 <21 (И •- 1)" (II + К). (XIII. 17)

п= 2

Используя коэффициенты разложения аномалий силы тяжести в ряд по

сферическим функциям, полученные И. Д. Жонголовичем, в ЦНИИГАиК по

формулам, приведенным выше, были выполнены расчеты, характеризующие

поле аномалий силы тяжести до восьмой степени включительно.

В табл. 34 представлено влияние гармоник различной степени на средние

квадратические значения аномалий силы тяжести, высот квазигеоида и укло-

нений отвеса.

Таблица 34

Влияние гармоник порядка

Влияние гармоник от 2 до та порядка

та

, мгл

Еп.*

(г, мгл

1/2

±7,8

9.8

3,5

2,8

3,7

• 2,2

2.9

±50,7

31,9

7,6

4.6

4,8

2,4

2.7

±4,02

3,57

1,10

0,81

1,01

0,58

0,74

±7,8

12,5

13,0

13,3

13,8

14,0

14,3

±50,7

59,9

60,4

60,6

60.7

60.8

60,9

±4,02

5,38

5,49

5,55

5,64

5,67

5,72

Табл. 34, таким образом, дает представление о порядке величины средних

квадратических значений аномалий силы тяжести, высот квазигеоида и укло-

нений отвеса на Земле. Эти величины в рассматриваемом случае соответственно

оказались равными: ±14,3 мгл, ±60,9 м, ±5,72".

В табл. 35 приведены данные, которые характеризуют влияние аномалий,

выражаемых сферическими функциями степени от 2 до п, на средние квадрати-

ческие значения величин Д^ и (Д|

+ Дг]

)

/*.

Таблица 35

ДЕ, м

[(д|"

+ ЛгГ

)

1/2

•Ф. "

0° 11,5°

23,1°

34,9°

0°

11,5°

23,1°

34,9°

2 +50,7 ±38,9 ±29,7

±26,1

±4,02 ±3,08

±2,36

±2,07

3 59,9 42,6

30,6

26,5

5,38 3,64

2,50

2,13

60,4 42,6

30,6

26,5

5,49 3,66

2,50

2,14

60,6 42,7

30,6

26,5 5,55

3,66

2,51 2,14

60,7 42,7 30,7 26,6 5,64 3,66

2,53

2,15

60,8

42,7 30.7

26,6 5,67

3,66

2,54

2,15

60,9

42,7 30,7 26,6 5,72 3,67

2,54

2,15

365.

Влияние аномалий, выражаемых сферическими функциями степени ет -»

до п на средние квадратические значения величин

А'С,

и (А|

+ Дт]

)

1/г

, пока-

зано в табл. 36.

Таблица

Д&, м

Фо

0°

11,5°

23,1°

34,9°

0°

11,5°

23,1° 34,9"-

±7,6 ±2,6

±0,3

±0,6

±1,10

±0,37

±0,05

±0,09

8,9

2,7

1,0

1,37 0,39

0,19 0,17

6 10,1 2,7

1,8

1,3

1,70

0,39 0,37 0,23

7 10,4 2,7 2,0 1,3

1,80 0,40 0,42

0,24

10,7

2,8

2,1

1,3

1,94 0,46 0,46

0,24

Эти таблицы наглядно иллюстрируют эффект, достигаемый в результате

улучшения сходимости ряда Стокса. Уже при ф

= 11,5° прирост поправок

с увеличением п значительно слабее, чем при -ф

= 0, особенно это проявляется

при ф

= 23,1 и 34,9°.

Из табл. 35 видно, что если интегрировать до сферического расстояния

= 23,1° (2550 км) или ф

= 34,9° (3820 км) от определяемого пункта, то

среднее квадратическое влияние всех дальних зон на высоты квазигеоида

и уклонения отвеса составляет соответственно ±31 м и ±2,5" или ±27 м и

±2,2".

Если коэффициенты разложения аномалий силы тяжести, входящие в сфе-

рические функции второй и третьей степени, считать известными и с их по-

мощью учесть влияние гармоник 2 и 3-ей степени на величины Д^ и (АЕ

—

+ Дг]

)

^ то и среднее квадратическое влияние дальних зон на высоты квази-

геоида и уклонения отвеса, обусловленное только сферическими функциями

четвертой степени и выше, значительно уменьшится. Как следует из табл. 35.

в этом случае при учете аномалий в пределах сферической зоны радиуса ф

—

= 23,1° или 34,9° влияние дальних зон соответственно будет составлять ±2,1 м

и ±0,5" или ±1,3 м и ±0,2".

§ 80. ДИСКРЕТНОСТЬ МИРОВОЙ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ,

ТОЧНОСТЬ ВЫВОДОВ УКЛОНЕНИЙ ОТВЕСА

И АНОМАЛИЙ ВЫСОТЫ

Формула ошибки представительства (Х.З) дает возможность рассчитать

точность выводов уклонений отвеса и аномалий высоты при заданном распо-

ложении гравиметрических пунктов. При этом вычисления следует начи-

нать со сферического расстояния я]),,, так как гравиметрическую съемку в ради-

усе 2 тыс. км (ф

= 18°) можно сделать такой плотности, при которой она

полностью обеспечит требуемую точность.

Итак, положим, что вся поверхность Земли сферическими радиусами ф

, . . ., разбита на п зон, а каждая зона с номером к — на равные между

собой трапеции, равновеликие квадрату со стороной, равной ширине данной

зоны ф* — ф/г_1*

366.

Средняя линия этой трапеции должна быть равна ее высоте, т. е. должно

соблюдаться условие

ДЛ^зт

яЬ

ср

= % —

где

= 4" +

^А-а)'

АА

= А

— А

—

разность азимутов, ограничивающих трапеции зоны с номером к.

Число трапеций в этой зоне будет

Тогда

Жзт^+вш^) (XIII.18)

ДЛ

= —= . (XIII. 19)

Пусть в каждой сферической трапеции имеется один гравиметрический

пункт. Поскольку

1/аГ

= ]/~у =

ошибка представительства от такой трапеции в зоне к в соответствии с (Х.З)

будет

= 2

1/(%-1|>,_

) Я, (XIII.20)

где Е — радиус Земли.

При вычислении высот квазигеоида по формуле Стокса (VII

1.53)

и укло-

нений отвеса по формулам Венинг-Мейнеса (VIII.57) каждая сферическая

трапеция будет вносить ошибку в аномалию высоты, равную

Е = 1| (XIII.21)

а в составляющую уклонения отвеса

1 * /. л „ , , Г й

д.=

1 (ХШ.22)

Н-1

В выражении (XIII.22) составляющая уклонения отвеса вычисляется по

произвольному направлению. Поэтому надобность в вычислении составляющей

в первом вертикале отпала. Подставив в (ХШ.21) значение б^з из (XIII.20)

и ДА

из (XIII.19), получим

А^

сд8/г

? (XIII.23)

Заменим в (XIII.22) разность косинусов ее средним квадратическим зна-

чением в зоне по формуле

соз А

—

соз А

2 (соз А

—сов Ат-!)*

т=1

367.

но

К ' к

^(соаА,

—

соз4

_х)

= 2(

281П

-\-Ат+1 • Ат—Ат-\ \

•

81П

-т=1

|/ 2

281

1 т= 1

зт

ср

Заменив 2 зт

ср

через 1 — соз 2А

СХ)

, можно доказать, что

2 2 зт

ср

= У 1

Поскольку в соответствии с (XIII.19)

Л.4 . п

31Н

—г— =

81И

— ,

2 1к

получим

соз А

— сое А„

У 2

зт

г к

По малости угла л/г

положим зт (л/г

) л/1

и с учетом (XIII.18) окон-

чательно получим

соз А

— соз А

= У 2 —

8Ш +

8Ш 1))^-

Теперь (XIII.22) принимает вид

сЛ'/.

АЕ =

Лу • 81П

(3111 ф/г

8111 Я^-х)

^ ^

•к-1

1 -й-зт^йгр

или в линеинои мере

К 31П1"А;

СП*'*

У2пу (81П +

81П

СЧ>А—ФА

-х)

3/г

111^-1) Л

аз

(XIII.24;

Каждая трапеция зоны к с одним представительствующим пунктом внесет

ошибку Ат в положение определяемого пункта

Дт.

= А

+ Я

вт

1"Д|.

(XIII.

2.=

А т

Подставляя в (XIII.25) из (ХШ.23) и (ХШ.24), получим

2ДЗ (фа—^)»

Ч \

] 5

(г|?)

апиМФ ) I

81п

^ ^

(ХШ>-

368.

Поскольку суммарная ошибка для всей зоны к будет Ат с учетом

(XIII.

18)

получим

( Ч V

/ % \

Л^

(8111

-I- 81П

^к-Х)

М* =

с2ПЗ

У УРк-Ък-О*

к" 1

Средняя квадратическая ошибка в положении пункта, вызванная всеми

имеющимися трапециями, будет равна

Ч \

/ % у

/ /

(ХШГ27)

Формулы (XIII.26) и (XIII.27) позволяют решить вопрос о наивыгодней-

шем распределении пунктов мировой гравиметрической съемки.

Еще в 1935 г. Грааф Хентер пришел к выводу, что для определения вели-

чин, обусловленных гравитационным полем Земли, необходимо иметь съемки

двух типов:

1) общую мировую гравиметрическую съемку со станциями, равномерно

расположенными на поверхности всего земного шара;

2) местные гравиметрические съемки с соответствующей плотностью стан-

ций в окрестностях определяемого пункта.

При расчетах оптимального распределения гравиметрических станций

Грааф Хентер исходил из условия, чтобы влияние каждой станции на среднюю

квадратическую ошибку вывода было бы одинаковым, т. е. чтобы при всех

значениях к от 1 до п

Лт

= СОП81. (XIII. 28)

По мнению Граафа Хентера, большую практическую пользу могла бы

иметь общая мировая гравиметрическая съемка с плотностью один пункт на

трапецию размером 5x5°. Это предполагает наличия всего 1654 пункта. При

такой съемке по расчетам Граафа Хентера высота геоида могла бы быть полу-

чена с ошибкой ±10,4 м. При наличии дополнительной съемки сгущения

радиусом 20°, состоящей из 84 пунктов, ошибка определения аномалии высоты

уменьшится до ±7,0 м.

Составляющие уклонения отвеса | или т], выведенные по результатам

общей мировой гравиметрической съемки (1654 пункта) и дополнительной

съемки сгущения (84 пункта), получаются по данным Граафа Хентера с ошиб-

кой ±0,35".

В. В. Броваром [2] показано, что наивыгоднейшее распределение пунктов

будет обеспечено в том случае, если будет соблюдено условие

= 4*) = тш, (ХШ.29)

к=1

где каждое слагаемое в М

— функция двух переменных

г|з

и а два смеж-

ных слагаемых связаны между собой значением переменной

Средняя квадратическая ошибка в положении определяемого пункта

(ХШ.29) минимальна, когда г|?„, . . . являются корнями системы уравнений

4^ = 0, (ХШ.ЗО)

24 Заказ 1379

369