Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

где к = 1, 2, ... п — 1. Эта система имеет сложный вид и решается метод:*

последовательных приближений.

Преобразуем выражение (XIII.30), сократив его на постоянный множи-

тель с

/яу

^к У к 1

125^) вт% ^ Я(ф)зтгМф + -^^- зт ф |

т йг|5 X

% \

^ Я(ф)зтфйф +1 ^ X

! / ]

С +1

^ 18111%+

81П1|)Ц (8111г|)

+8Ш

^-х)

Т Т

3111

Ярд. +81П фй-

Г йпгЫгь!

л^к

Т Т

| (зт^./г+х+

8П1 гр/г)

к+1

й+Х \ "

5 (ф)зшф $ |Х

Г 2(%

+х

—ф

) С08%

8111

Ч|З

й+1

+81пг|Э

~Г

(8111 я|3

+ 31П

^ "

Отсюда видно, что каждое уравнение (XIII.30) содержит три неизвестш.-!:

% И Я^х-

Введем обозначение

= Р (%_!, %

х).

Неизвестные можно представить в виде

$ь = Шо

—

к,

где (ф/,)

— приближенное значение *ф

Тогда

ФА-1 = ('ФЙ-ОО +

к-1

% = ("ФА)О -г

%+1 = (4^+1)0 +

к+1-

Разложим функцию (Ш"

/бф

в ряд и ограничимся первыми членами ра

• -

ложения

.370

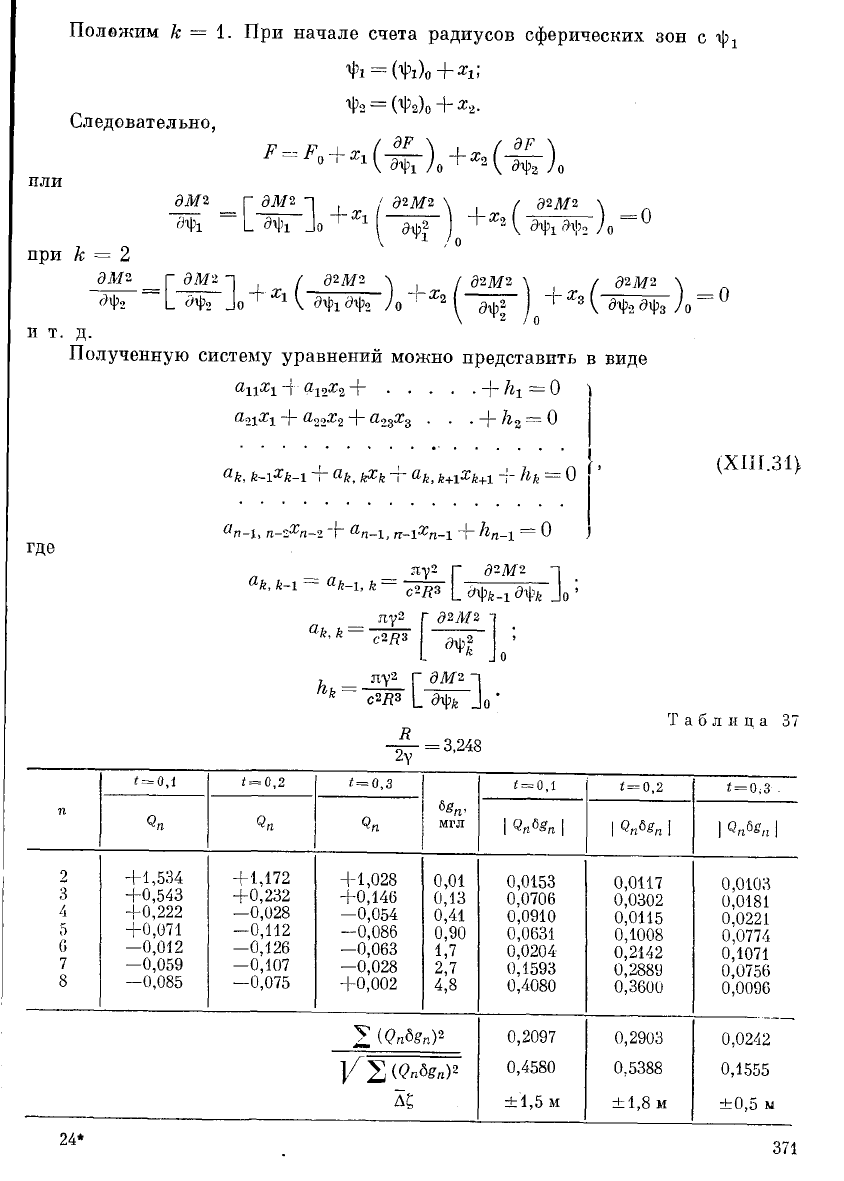
Полежим к = 1. При начале счета радиусов сферических зон с

Следовательно,

дМа _ Г дМ* П ( дШъ \ / 32Л/2 \

-Ьэ^! _|о () 1 )

ЭМ2 _

дМ2

/ Э2М2 \ /92М2 \ / 92Л?2 N

<*Ч>2 1_ Л(>2

"Г-

ЛЬ Л '

^"^ф

" ] I дфз Л

= 0

или

при к = 2

амг г

и т. д.

Полученную систему уравнений можно представить в виде

«11^1 4

+ + к

+ а

. . . -)- /г

— О

где

24*

й-1^-1 + я*, А -Г

к>

к+1

+ к

= 0 '

п-^п-1

п-1, +

^л-1

—

(XIII.31)

к,

к-

к-1,

Я.у2 Г дЗД/2

С2ДЗ [ д^Тд^

Яу2 Г 52Д/2

ь —

9Л/2

Пк

- С2ЛЗ _]

•

3,248

а б л и ц а

' = 0,1

( = 0,2

< = 0,3

< = 0,1

г = о,2

« = 0,3 .

ёп<

мгл

«А

1 <*п*в„ |

«А

+1,534

+0,543

+0,222

+0,071

—0,012

—0,059

—0,085

+1,172

+0,232

—0,028

-0,112

-0,126

-0,107

—0,075

+1,028

+0,146

—0,054

—0,086

—0,063

—0,028

+0,002

0,01

0,13

0,41

0,90

1,7

2.7

4.8

0,0153

0,0706

0,0910

0,0631

0,0204

0,1593

0,4080

0,0117

0,0302

0,0115

0,1008

0,2142

0,2889

0,3600

0,0103

0,0181

0,0221

0,0774

0,1071

0,0756

0,0096

2 «?пбе

0,2097

0,2903

0,0242

У 2 ш

Ьв

)

0,4580

0,5388

0,1555

ДБ

±1,5 м

±1,8 м

±0,5 ы

371

Решение системы (XIII.31) позволяет установить оптимальное распреде-

ление пунктов мировой гравиметрической съемки. Для ориентировочное

оценки ошибка определения влияния аномалий дальних зон на высоту квази-

геоида можно использовать формулу (XIII.14), заменив в ней порядков^

дисперсии аномалий силы тяжести §

порядковыми дисперсиями их ошибок 6 г

В табл. 37 в качестве примера приведены результаты соответствующих вычисл—

ний. Значения величин 8§

взяты по данным Гапошкина [12], а коэффициен-

тов ()„ — из табл. 31.

§ 81. ФОРМУЛЫ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

СИЛЫ ТЯЖЕСТИ

Первыми параметрами, определенными по гравиметрическим данных

были коэффициенты у

и (3 нормальной формулы, а следовательно, и сжатие -

Редкая и крайне неравномерно расположенная на поверхности Земл:

гравиметрическая съемка конца XIX и начала XX вв. не могла быть испол

зована для сколько-нибудь надежного определения других параметров.

Больше того, неоднократные определения у

и р (а значит и сжатия Земли

не отличались однозначностью, поскольку различные авторы использовал:

неодинаковый и в количественном и в качественном отношении исходный гравг

метрический материал.

Определение коэффициентов нормальной формулы производилось по сг

собу наименьших квадратов, при этом за наблюденную величину принимал}

так называемую силу тяжести, приведенную к уровню моря, т. е. величин

= $ + к

к, где

Ь,

— высота точки наблюдения над уровнем моря, а к —

вертикальный градиент нормальной силы тяжести.

Эта величина и вводилась вместо

"у

в нормальную формулу силы тяжвст»

которую представим

«Го

Уе

УгР

81п2

Ф — ?А

81П

Ф-

Замена величины у

величиной вносит в нормальную формулу

сил ^

тяжести ошибку, намного превосходящую возможную ошибку наблюден:'!

а именно — ошибку порядка аномалии силы тяжести §—у. Весь расчет

делал с =

на то, что при большом числе гравиметрических пунктов, покрывающих в>:

можно большую часть поверхности Земли, ошибки будут подчиняться закол

случайных ошибок так, что определенные по способу наименьших квадрат =

вероятнейшие значения коэффициентов у

и будут близки к истинным. I:

тий коэффициент нормальной формулы (З

обычно находился из теоретичесг!:

расчетов, поскольку по своей малости он не мог быть определен достаточ?

надежно по результатам гравиметрических наблюдений. Так, например, Гол •

мерт определял его по формуле типа (IV. 22), принимая определенную гипот-.

о распределении плотности внутри Земли. Можно его вычислить и по

форму

^.18). Поэтому при определении неизвестных у

и (3 коэффициент считал г

известным и включался в свободный член уравнений ошибок, которые и.м-..1

вид

где

< = — (ф<) + РЛ зт

2ф],

Ьг

= 81П

ф/.

372.

Покажем, как можно определить коэффициенты у

и р при сравнительно

небольшом числе пунктов.

За неизвестные, которые определяются по способу наименьших квадратов,

принимаются

, У

Ус$-

Отметим, что у имеет простой физический смысл, а именно:

У = У Р~Уе-

Уравнения погрешностей напишем в обычном виде

х +

= и

+ ъ

у + и = у о

х +

ЪпУ

= »п-

Нормальные уравнения в общем виде запишем как

[017]

О,

[Ьу]=0.

В данном случае можно уменьшить число нормальных уравнений до

одного, воспользовавшись тем обстоятельством, что коэффициенты при неизвест-

ном х в уравнениях погрешностей а = 1 и, следовательно, [у] = 0.

Получим вспомогательное уравнение, в котором все коэффициенты при

неизвестных и свободный член будут являться средним арифметическим из

всех п значений

га я

Теперь, вычитая из каждого уравнения погрешностей вспомогательное,

получим преобразованные уравнения погрешностей вида

у + В

= и

В«у-

]

г Ьо

-----

V*,

[Ь]

где В

—

В результате получим одно нормальное уравнение

[ВВ] у + [ВВ]

---

-О,

решением которого будет

[ВЬ]

' [вв] '

373.

После этого неизвестное х определяется из вспомогательного уравнения

Зная х и г/, легко определить р, поскольку, очевидно р = у]х. Сжатие а

находится по формуле (У.25).

Определение коэффициента д — со

а/у

не вызывает трудностей, поскольку

делений с высокой степенью точности и ее ошибкой в данном случае можно

пренебречь, а большая полуось эллипсоида а нужна с той же степенью точности,

что и сама величина д.

Это утверждение легко проверить. Логарифмируя, а затем дифференци-

руя выражение для д, получим

1п

д —

1п со

-)-

1п а

—

1п

Ад Аа Ау

Ч а у

~ а

Величина д, как и величина Р, имеет порядок сжатия Земли и опреде-

ляется с точностью до четырех значащих цифр. Значит, с такой же точностьк

необходимо знать и большую полуось а, т. е. с ошибкой На 1 км.

Из множества нормальных формул, полученных различными авторам*

в разное время, приведем прежде всего нормальную формулу Гельмерта 1901

—

1909 гг.; в настоящее время она принята в СССР для вычисления нормальной

силы тяжести

= 978,030(1 + 0,005302 зш

В-0,000007 зт

2Б), (ХШ.5-

где

= 978,030 гал,

р =0,005302,

р! = 0,000007.

Если нормальную формулу представить многочленами Лежандра (111.28 .

то получим другую форму записи формулы Гельмерта

= 979,75485 + 3,45440Р

(зт В) + 0,00626Р

(зтЯ). (ХШ.Ж-

Гельмерт получил свою формулу в результате обработки наблюдений

силы тяжести, произведенных на 1603 пунктах. Сжатие, соответствующе*

формуле Гельмерта (определенное по формуле (У.25) при р = 0,005302, оказа-

лось равным

а=

"298Т '

т. е. практически совпадающим со сжатием эллипсоида Ф. Н. Красовског-

В 1930 г. на съезде Международного геодезического союза в Стокгольме в ка-

честве международной формулы была рекомендована формула Кассиниса

= 978,0490 (1 + 0,0052884 зт

В - 0,0000059 зт

2В),

которая соответствует эллипсоиду Хейфорда со сжатием а = 1/297,0. Коэф-

фициенты Р и р

формулы Кассиниса вычислены для этого эллипсоида по фор-

мулам (У.25) и (У.18). Постоянная у

получена из измерений силы тяжестх.

374.

В настоящее время коэффициенты нормальной формулы силы тяжести

определяют в комплексе с другими фундаментальными геодезическими пара-

метрами, о чем будет сказано ниже (см. § 85). В заключение приведем нормаль-

ную формулу силы тяжести, соответствующую фундаментальным геодезическим

постоянным, принятым на XV Генеральной ассамблее Международного геоде-

зического и геофизического Союза в г. Москве в 1971 г.

= 978,0318 (1 + 0,0053024 зт

В - 0,0000059 зт

2В).

Новая формула отличается от формулы Кассиниса с учетом поправки

Потсдамской системы с 14 мгл на (—3,2 + 13,7 зт

В) мгл.

Переход той или иной страны к новой нормальной формуле силы тяжести

связан с перевычислением большого числа накопившихся ранее гравиметри-

ческих данных, с изменением гравиметрических карт и каталогов. Потому,

учитывая чисто служебный характер нормальной формулы, не следует прибе-

гать к частому изменению ее коэффициентов. В случае необходимости проще

вводить соответствующие поправки в конечные выводы.

§ 82. СВЯЗИ МЕЖДУ КОЭФФИЦИЕНТАМИ РАЗЛОЖЕНИЯ

ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ РАЗЛИЧНЫХ ХАРАКТЕРИСТИК

ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ

Выразим коэффициенты разложений в ряды по сферическим функциям:

возмущающего потенциала, высоты квазигеоида и составляющих уклонений

отвеса через коэффициенты разложения аномалии силы тяжести.

При этом будем предполагать, что нормальный потенциал выбран таким

образом, что разложение возмущающего потенциала в ряд, как и аномалий

силы тяжести, начинается с членов второго порядка, т. е. удовлетворяются

условия

ёср ~Уср

(XIII.34)

^(0,

А,)

= 0 )

В этом случае разложение для аномалий силы тяжести (VIII.28) прини-

мает вид

ё-У = 2епФ, Д (XIII.35)

п=2

где

ёп (0, Ц = 2 (Л

пк

соз кХ + В

пк

зт

к%)

пк

(0), (ХШ.36)

к=0

" = Т И С -

а» МР

(6')

йсо

(XIII.37)

375.

Представим разложения для возмущающего потенциала и высоты квази-

геоида в виде

Г = 2 2 (Д„*

С08

кк + Е

пк

(81П

кк) Р

пк

(9),

П=2Й=0

СО П

Й=0

(XIII.38)

(ХШ.39:

Для того чтобы выразить коэффициенты этих разложений через коэффи-

циенты А

пк

и В

пк

разложения аномалии силы тяжести, используем формулы

§ 79.

(0,

Х)

п—1

ие,

Тогда на основании (XIII.40) и (XIII.41) имеем

Я Я

пк

а-пк'-

п — 1

±пк

Я А

пк

РлА

п — 1

Я Впк

к>

(XIII.40

(XIII.41

(XIII.42'

(XIII.4о

у а — 1 ' гпг. у

—

Получим наконец, формулу для разложения составляющих уклонение

отвеса в ряды по сферическим функциям. Если в формулы (VI.8) вместо Т

подставить то в соответствии с (VI.

19)

получим формулы для составляющих

отвеса

Р оф

ЯСС ф

д\

(XIII.

р дк

Заменив в (ХШ.39) 6 через 90—<р и произведя дифференцирование ряд»

по широте и долготе, получим

со п

I = — зес

2 (

'пк

соз к к +

пк

зт кк) Р

пк

{

ф) -

п-2

к^а

со п

+ 2

2 (

'пк

соз кк 4 - 31П кк) Р

пк

(ф)

и»2 к:-0

со п

= — зес ф 2

2 (

'пк

соз кк -\ - р^' зт кк) Р

пк

(ф)

п=2 к= о

(ХШ.

где коэффициенты связаны следующими соотношениями с соответствующими

коэффициентами ряда (XIII.35):

_ л

(я+А+1)

(л + А+1)

пЬ ~

п+1,Ь Рпк — &п+1,к

уп

а-пк

а'пк

Яп

у (п — 1)

Як

Ч(п— 1)

•В

пк

; р

Яп

пк '

пк

у{п — 1)

—Як

<»—1)

пк

(XIII.:

Выражения (XIII.42), (ХШ.43) и (XIII.46) устанавливают связь между

коэффициентами разложения по сферическим функциям основных характери-

стик гравитационного поля Земли и позволяют через коэффициенты разложе-

ний аномалии силы тяжести получить коэффициенты других разложений путем

простого пересчета, не прибегая в каждом случае к интегральным формулам

(Ш.ЗО).

Выразим теперь коэффициенты различных разложений через коэффициенты

к И З

пк

Если возмущающий потенциал представлен в виде

оо п

т =^^^(с

пк

с08кХ +

8пк

зткХ)Р

пк

(В), (ХШ.47)

2 к=О

то, как показано в § 76,

оо п

Ы соз кХ + з

пк

зт кХ) Р

пк

(9). (XIII.48)

п=2

й." О

Сравнивая коэффициенты при соответствующих сферических функциях

в рядах (XIII.39) и (XIII.48), находим

пк

= Яс

пк

Получим теперь разложение в ряд по сферическим функциям аномалии

силы тяжести с коэффициентами с

пк

и з

пк

Сравнивая (VIII.18) и (XIII.47), находим, что между сферическими функ-

циями одного и того же порядка должно существовать соотношение (при

р = а = Я)

•

{Спк 008 кх + 8пк з1п Рпк

Й=о

Следовательно,

= ЩЯ

{Спк

соз

кХ

+ з

пк

ЯП

кХ) Р

пк

(9).

к= о

Подставим значение У

(0, Я) из (VIII.21). С учетом рИ/Я

= у, получим

ёп =

(п

—

{Сак СОЗ кХ

пк

31 п кХ) Р

пк

(0).

к=О

Теперь разложение аномалии силы тяжести (VI11.28) можно представить

со п

{8—У) = {8 —

У)ср

+ У 2(»-1) (с

пк

соз

кХ

+ з

пк

8шкХ)Р

пк

{В),

(XIII.50)

п-2 к=о

где у — среднее значение нормальной силы тяжести.

Сравнивая (УШ.28), (ХШ.36) с (ХШ.50), находим

пк

= у(п-1)с

пк

.к —

У(

—

пк I

(ХШ

01)

377

§ 83. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ

СИЛЫ ТЯЖЕСТИ ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ

Представим нормальную силу тяжести и аномалии силы тяжести в виде

известных разложений по сферическим функциям. Мы имели [см. (У.20) и

(XIII.35)]

То

0 (

С03 0

) +

* (

С08 0

) +

А0

О>

(

С08 0

со п

«•

—

7=2

(Апк соз кк + В

пк

зт кк) Р

пк

(9),

п=2 к'о

сложив эти выражения, перейдем к разложению силы тяжести

со п

Е + КК = у

+ 2 2 (

пк соз к а + В

пк

зт кк) Р

пк

(0), (XIII.52'

п=2 к-о

где под знаком двойной суммы должны отсутствовать полиномы Лежандр^

второй и четвертой степени, поскольку они вошли в выражение для у

В левой части (XIII.52) член к

к означает редукцию в свободном воздухе.

— вертикальный градиент нормальной силы тяжести, к — высота ТОЧКЕ

наблюдения над уровнем моря. Сила тяжести, наблюдаемая на физической

поверхности Земли, обнаруживает отчетливую зависимость от высоты Л.

поэтому прежде чем представлять ее рядом сферических функций необходимо,

вводя редукции к

к, освободить ее от этой зависимости.

Для определения коэффициентов А

пк

и В

пк

разложения (XIII.52) тре-

буется наличие мировой гравиметрической съемки. Плотность этой съемки

зависит как от степени п сферической функции, которой приходится ограничи-

вать разложение (XIII.52), так и от точности, с которой требуется выполнпт:-

разложение.

В качестве примера рассмотрим методику определения коэффициенте!

разложения аномалии силы тяжести в ряд по сферическим функциям, раз-

работанную И. Д. Жонголовичем.

И. Д. Жонголович принял специальную разбивку земной поверхности

на трапеции, строго эквивалентные друг другу по площади. Для этого специ-

ально подобранной системой параллелей поверхность Земли разделена на

зоны, а каждая зона отрезками равностоящих меридианов разделена на неко-

торое количество секторов, различное в каждой зоне.

Расчеты делались по формуле для сферы

па = 2л (зт ф

— зт ф

где ф

и ф

— широты южной и северной границ зоны; ст — площадь каждого

сектора, считая радиус шара равным единице; п — число секторов в зоне.

Сначала была произвольно задана величина а = 4я/410, что "соответствует

площади, приблизительно равной трапеции на экваторе со сторонами по 10

затем расчет велся от экватора и состоял в последовательном подборе таких

целых значений п для каждой зоны, чтобы широта ее северной параллели ф.

отличалась от широты южной ф

на угол, возможно более близкий к 10".

Каждая из таких «десятиградусных» трапеций делилась на 100 «одно-

градусных» при помощи соответствующих меридианов и параллелей. Вся

поверхность Земли, таким образом, была разделена на 41 000 одноградусны!

трапеций, каждая площадью около 1250 км

378.

Начальная стадия обработки всего материала состояла в получении про-

стых средних значений как аномалий силы тяжести, так и соответствующих

высот всех пунктов, расположенных в каждой «одноградусной» трапеции. При

этом получение гравиметрических характеристик для «десятиградусных» тра-

пеций проводилось двумя различными способами.

В первом способе средние значения аномалий в трапециях 10x10° вычис-

лялись как простое среднее из средних значений аномалий в «одноградусных»

трапециях

Во втором способе учитывалась зависимость аномалий силы тяжести от

высот гравиметрических пунктов (см. § 37).

В результате для каждой «десятиградусной» трапеции были вычислены

средние аномалии по формуле

для суши Д^

—

-\-Ък

ср

для моря А§' — я

+ Ъ'к'

ср

где к

ср

и к'

ср

— значения средних высот и глубин в каждой «десятиградусной»

трапеции.

Значения Д^ были получены для 151 трапеции, а — для 118.

Эти величины использовались далее для вычисления окончательных грави-

метрических характеристик «десятиградусных» трапеций по второму способу

Величины Д,д

были получены следующим образом: для чисто континен-

тальных трапеций (а = 1,00) Д^

принято непосредственно равным значению

А§, для чисто океанических трапеций (Р = 1,00) Д^

принято непосредственно

равным значению А§'; для трапеций смешанного типа, в пределах которых

имеется и суша, и море, применялась формула

Если в данной трапеции из имеющихся наблюдений была получена лишь

величина Д^ для суши, то окончательная гравиметрическая характеристика А§

вычислялась по формуле

Д^

= +

(Д? -

Ък

+ 19 +

Ъ'к")

= + р (19 -

Ък

+ Ъ'к').

Если в данной трапеции из наблюдений была получена только величина Ад'

для моря, то

Д^

= а (А

° - Ъ'к' -19 +

Ък)

+ рД^' = V - а (19 -

Ък

+ Ъ'к').

Систематическая разность а

— а

принята равной +19 мгл. В тех трапе-

циях, где местные значения

Ъ'

не определялись, брали их средние значения:

= +46 и Ъ' = -20.

Из 410 «десятиградусных» трапеций только 204 получили гравиметриче-

ские характеристики Д^ и Д^

Разложение аномалии силы тяжести Д^ и силы тяжести § И. Д. Шонго-

лович представил

(А

пк

соз кХ + В

пк

8111Щ Р

пк

(6), (XIII.53)

п=о к=о

$ = 979754,85 + 345440Р, (соз

+ 6,26Р

(соз 6) + А§. (ХШ.54)

379.