Шимбирев Б.П. Теория фигуры Земли
Подождите немного. Документ загружается.


В последнем интеграле взят знак минус по той причине, что внешняя нор-
маль п направлена на плоскости Оху в сторону отрицательных 2.
Поскольку потенциал точечной массы на поверхности сферы
т
, йт
1
Я '
получим
дТ , йт
дЯ ~~ ~ ' •
Если провести вспомогательную сферу Я = 1, то
6о = Я
2
(1(й,
где ш — часть поверхности вспомогательной сферы, соответствующая части
сферы а (Я), лежащей ниже плоскости 2 = 0. Тогда будем иметь
п (Н) о (й) а
При Я -*- ьо, со
-*•
2л, а интеграл по ограниченной части плоскости 2 = 0
переходит в интеграл по всей плоскости 2 = 0.
Таким образом,
+
СО
+оо
2| | йх йу. (XIV.
1
Если в точке С находится не точечная масса, а некоторое тело, то, сум-
мируя по всем элементам массы вт, тела и пользуясь свойством аддитивности
потенциала, найдем
+ 00 4-СЮ
2я/М
а
= | ^ ^Лхйу, (Х1У.2'
— оо -оо
где под Т следует понимать потенциал притяжения, создаваемый аномальное
массой М
а
. Поскольку, как мы условились, под аномалией силы тяжести пони-
мается вертикальная составляющая притяжения, то, очевидно, что
А ДТ
&
=
~дГ*
т. е. под интегралом в (XIV.2) стоит аномалия силы тяжести, создаваемая иско-
мым аномальным телом массы М
а
. Определим координаты центра инерция
тела (%
0
, г]
0
, ?„).
Рассмотрим интеграл
+ СО +ОЭ
— СО -СО
Поскольку на плоскости Оху потенциал Т точечной массы и его производ-
ная по
%
симметричны относительно проекции точки С на плоскость, то
+со 4-<х>
390.

откуда
-Ьоэ +со 4-со -рсо
* 1 $ 1 1 х^-йхйу.
— со —оо —00 -со
Учитывая (XIV.!), получим
+СО
-Г со
— со —со
Переходя от элемента массы йт к массе тела М
а
, находим
+ СО +СО
2Л/М
А
|
0
=| | Х^ЙХЙУ, (Х1У.З)
-оо -оо
так как на основании (11.29)
Аналогично получим
+
СО +СО
2я/М
а
т]
0
= ^ ^ У^йхйу, (Х1У.4)
-00 -00
Глубина залегания центра массы определяется по формуле Г. А. Гам-
бурцева, которую приводим без вывода,
+со +оо
6Л!М
А
1
Й
=\ ^ (Т + 2Т*^)ЙХДУ. (Х1У.5)
-со
—оо
При практическом применении формул (Х1У.2), (Х1У.З), (XIV.4) и (Х1У.5)
приходится ограничиваться интегрированием в некоторых конечных пределах.
Входящие в формулу (Х1У.5) величины Т и д^Т/дт?, как правило, непосред-
ственно не измеряют, а вычисляют через дТ/дг по интегральным формулам.
Применение столь сложных приемов определения при малой точности полу-
ченных результатов делается нецелесообразным. Для оценки глубины залега-
ния аномального тела может быть применен метод, идея которого была выска-
зана Ф. А. Слудским.
Так как направление вектора притяжения всегда проходит через притя-
гивающее тело, то вполне возможна пространственная засечка положения тела.
Правда, в общем случае направления векторов не пересекаются в одной точке,
но этот метод дает возможность ориентировочно оценить положение притяги-
вающего тела.
Для получения направления вектора притяжения следует вычислить
проекции этого вектора на координатные оси, учитывая, что дТ/дг = Ад.
дТ/дх и дТ/ду вычисляют по формулам для составляющих уклонений отвеса,
поскольку на основании (VI.7) имеет место зависимость
— = —?
дх ~
дТ
1Г—™
391.

Используя формулы для плоскости (IX.56) и (IX.57) и полагая в нп:
с1о = г (1г с1А, получим
оо 2 Я
дТ
дх
о о
5 ^-соаАйгбА,
о о
со 2Я
1 Г Г М.*ЪАЙГЙА.
ду 2д ^ ^ г
Для улучшения сходимости интегралов при малых г целесообразно Л.
уменьшить на постоянную величину Ад
0
, т. е. на значение аномалии в Т' :
точке, для которой вычисляются дТ /дх и дТ /ду. Получаем известные формул
-
:
Б. В. Нумерова
дТ
дх
ду -
дТ_ ^ | —А§-
0
о о
Дальнейшее построение засечки можно осуществлять графически п.~:
аналитически.
§ 88. ВТОРЫЕ ПРОИЗВОДНЫЕ ВОЗМУЩАЮЩЕГО ПОТЕНЦИАЛА
Эти производные, как и производные более высоких порядков от потек-
циала силы тяжести, играют важную роль при интерпретации, посколыг
они обладают гораздо большей чувствительностью по отношению к притяги-
вающим массам, нежели сами аномалии силы тяжести. Это объясняется те.",
что чем выше порядок производной, тем сильнее ее зависимость от расстояния
Так, например, если потенциал притягивающей точки У = / (т/г) есть функ-
ция, убывающая с расстоянием как 1 /г, то первая производная потенциала —
сила притяжения Р = йУ/Лг = —/
(т,/г
2
),
— убывает уже как 1 /г
2
, а вторе.-:
производная дРУ/йг
2
= 2/ (т/г
3
), как 1 /г
3
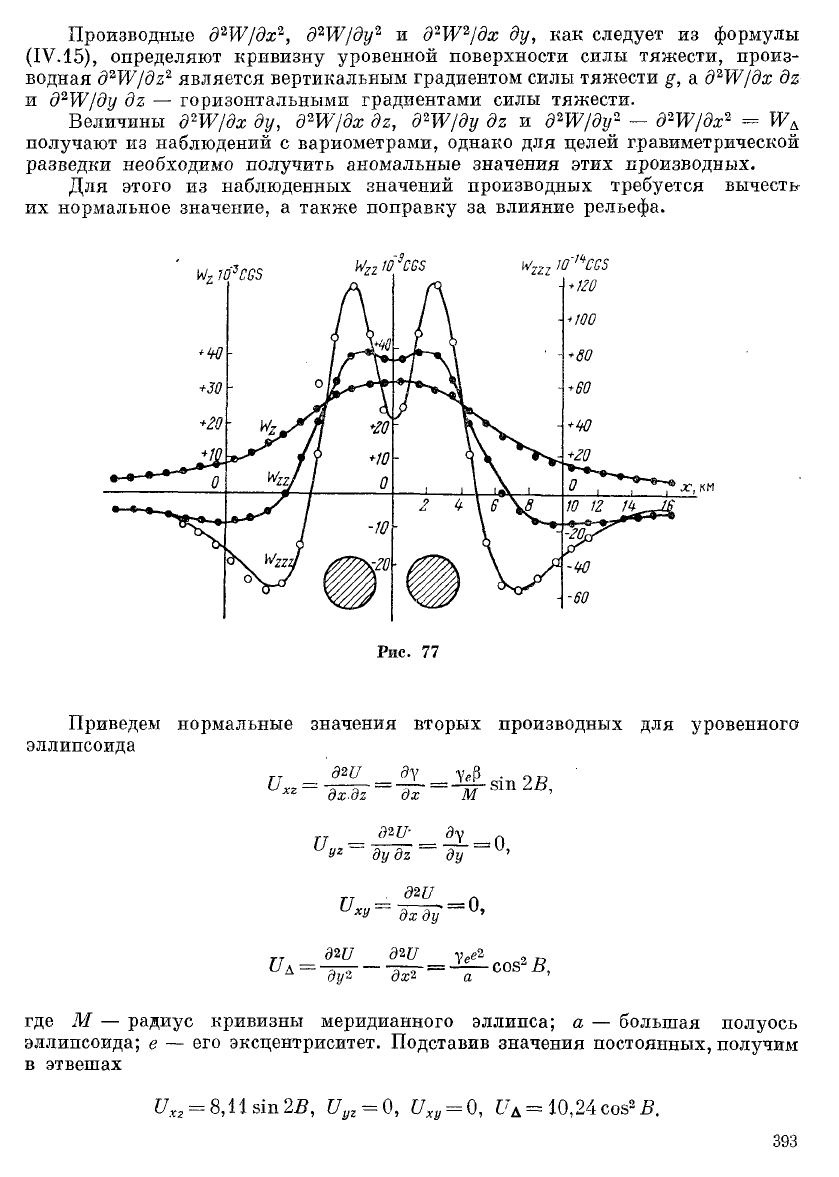
и т. д. На рис. 77 приведены г; -
фики изменения аномалии силы тяжести А§, ее вертикального градиент
д Ад/дг и второй вертикальной производной аномалии силы тяжести д
г
А§/о:-
от двух круговых цилиндров бесконечного протяжения. В приведенном примег
кривая Д^ не показывает наличия двух источников гравитационных аномалп;:
оно слабо проявляется и на поведении кривой д Ад/дг и только кривая д
2
ясно обнаруживает наличие двух аномальных масс.
Потенциальная функция силы тяжести УУ имеет шесть вторых производ-
ных, которые принято обозначать как
дх>±
Ухх
' ду2 д22
дхду дхдг
А
'
2
' ду д2 У
2
'
Эти производные потенциала имеют размерность 1/с
2
. Единицей изме;
ния является этвеш, составляющий 10"
9
(1/с
2
).
392
Производные д
2
УУ!дх
2
, д
2
1У/ду
2
и д
2
Ц>
г2
/дх ду, как следует из формулы
(1У.15), определяют кривизну уровенной поверхности силы тяжести, произ-
водная д
2
УУ/дг
2
является вертикальным градиентом силы тяжести а д
2
Ш/дх дг
и д
2
Ш/ду дг — горизонтальными градиентами силы тяжести.
Величины д
2
№/дх ду, д
2
Ц//дх дг, д
2
\У/ду дг и д
2
Ш/ду
2
— д
2
Ш/дх
2
=
получают из наблюдений с вариометрами, однако для целей гравиметрической
разведки необходимо получить аномальные значения этих производных.
Для этого из наблюденных значений производных требуется вычесть
их нормальное значение, а также поправку за влияние рельефа.
Приведем нормальные значения вторых производных для уровенного
эллипсоида
°
хг
- дх дг дх М
ау
и
У* дудг ду '
V =^ = 0
Х
У дх ду '
тт
дЮ дт
Уе
е2 ,
=
—^7,
=
СОЗ
2
В,
где М — радиус кривизны меридианного эллипса; а — большая полуось
эллипсоида; е — его эксцентриситет. Подставив значения постоянных, получим
в этвешах
V
хг
= 8,11 зт 2В, 11
уг
= 0,
Ь
Т
ху
= 0, П
А
= 10,24 соз
2
В.
393.

В табл. 43 приводятся нормальные значения производных.
Влияние рельефа учитывается при помощи формул, выведенных различ-
ными авторами (Этвеш, Швейдар, Никифоров, и др.), а также графическими
методами.
Аномальное значение второй
получается следующим образом:
производной, например величины IV
ху
где (\У
ху
)а — аномальное значение второй производной; \У
ху
— наблюден-
ное; Л
ху
— нормальное значение; {№
ху
)т — поправка за рельеф.
Однако в настоящее время вариометры в гравитационной разведке приме-
няются редко и их все в большей степени вытесняют высокоточные гравиметры.
Используя результаты наблюдений с гравиметрами, можно получить
горизонтальные градиенты аномалии силы тяжести: д Ад/дх и д А§/ду и вто-
рую вертикальную производную ано-
малии силы тяжести д
2
Ад/дг
2
.
Учитывая связь между аномалией
силы тяжести Д^ и возмущающим по-
тенциалом, можно написать
Таблица 43
в ил
и
ху
П
хг
•
и
Уг
0 10,2
0 0,0
0
10
9,9
0 2,8 0
20 9,0 0
5,2
0
30
7,7 0 7,7 0
40 6,0
0 8,0 0
50 4,2
0 8,0 0
60 2,6
0 7,0 0
70
1,2
0
5,2
0
80 0,3
0 2,8 0
90 0 0 0
0
дАе
д
дх дх
дАё
д
ду
ду
92
дг2
дг2
32 т
( дТ \ _ 83т ,
V дг а
2
з
—
"
По предложению М. У. Сагитова
[11] эти величины можно получить через
аномалии силы тяжести. Возьмем прямоугольную систему координат хОу
с началом в точке, где предполагается вычислить вторую вертикальную произ-
водную Т
ггг
; построим сеть квадратов со стороной 21. Координаты вершин
и центров полученных квадратов указаны на рис. 78. Поскольку горизонталь-
ные градиенты аномалий силы тяжести определяются как отношение разности
аномалий силы тяжести в двух соседних точках к расстоянию между нимп,
то для точек с координатами
будем иметь
(2' 2 )' ( 2' 2 )' ( 2 ' 2 )' ( 2' 2~)
1_ I \ _ А? (I, 1) + А
е
(I,
0)—Л^
(0, Р —
Ац (0,
0)
:
( 2 ' 2 )
21
_Ау(0.
Г)
+ А*(0, 0)—А^ (—I, 0)—А§ (—I, I)
Тхг
( 2 ' 2 ) 21
т
(1_ I \ А$ (I,
0)
+ А
е
(I, -0—А* (0, 0)—А*
(0,
-I)
Х2
\2' 2 ) ~ 21
«Ч 2 ' 2 )
А?(0, 0)+А^(0, -1)-А
ё
(~1, 0)—Д
?
(—г, -I)
21
(Х1У.6)
394.
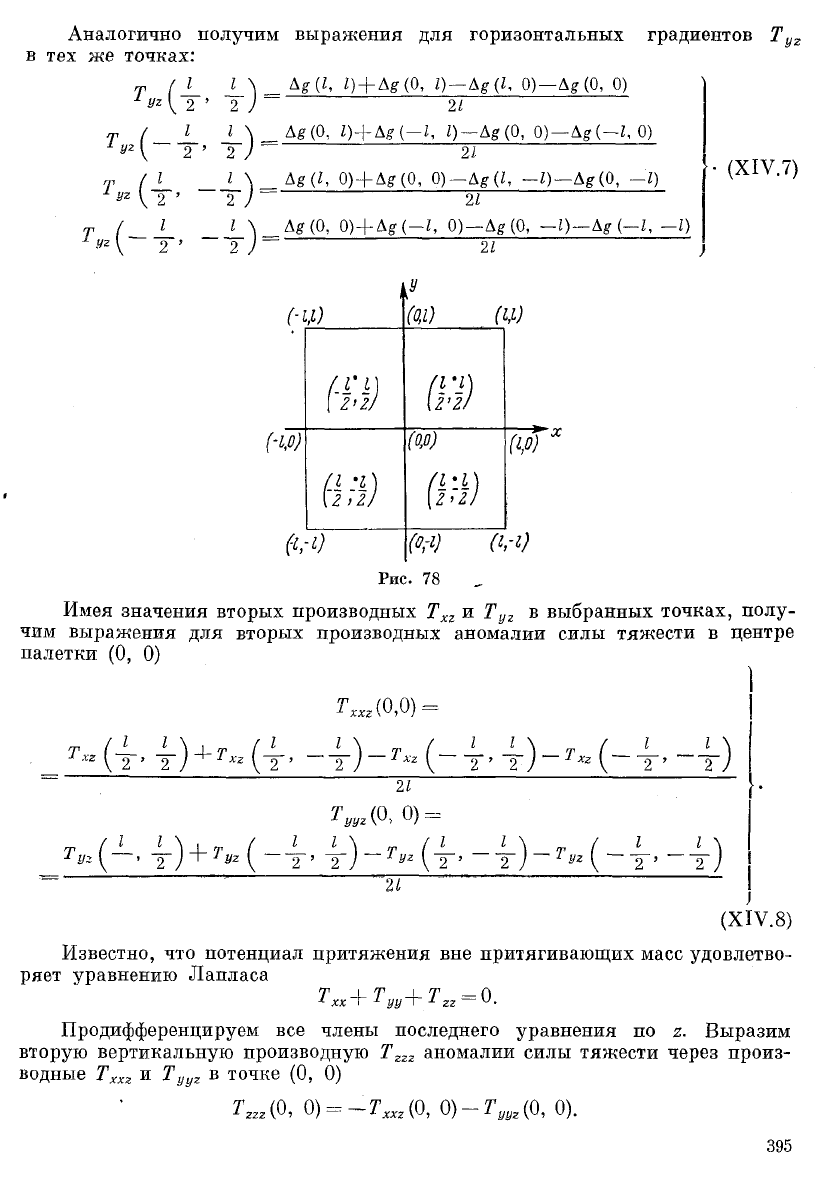
Аналогично получим выражения для горизонтальных градиентов Т
уг
в тех же точках:
АУ(*, 1) + А§ (0, 0)-ДУ(0, 0)
2/!
д*(0, г)+д*(-*, г>—а^г(о, о)-д
г
(-г, 0)
т
Уг (
г
г
2
Туг(
—
г
Т'
г •
г
2
, —
1 '
г
"2~
*
1
2
21
о)+д?(0, 0)— -о—Ду(о, -о
21
А*(0, <—Г, 0)—Д^(О, -Г)—Ду(-Г. -г)
г-^
(~2>г)
(П)
№
М
т)
до
(XIV. 7)
М 0,-1)
Рис. 78
Имея значения вторых производных Т
хг
и Т
уг
в выбранных точках, полу-
чим выражения для вторых производных аномалии силы тяжести в центре
палетки (0, 0)
Т
ххг
(
0,0)
=
т
Х
г (
т
,
+
(4-' —т)~
Тхг
(~Т' т)~
Тхг
(~~Т' ~т)
22
0) =
—• т)
+ Гг/2
( 2"' т)~
Туг
{т> ~т)~
туг
{~т> ~т)
>
(Х1У.8)
Известно, что потенциал притяжения вне притягивающих масс удовлетво-
ряет уравнению Лапласа
ТXX Т
уу
-С Т
22
= 0.
Продифференцируем все члены последнего уравнения по 2. Выразим
вторую вертикальную производную Т
ггг
аномалии силы тяжести через произ-
водные Т
ххг
и Т
ууг
в точке (0, 0)
7^(0, 0) = -Г
ххг
(0, 0)-Г
да
(0, 0).
395.

Принимая во внимание соотношения (Х1У.6), (XIV.7) и (XIV-8), в нос.
-
нем равенстве выразим Т
ххг
и Т
ууг
через аномалии силы тяжести Ад.
Т- (0 0)—О—А*
(Л
-0—Ау(-г. 1)-&
В
(-1, -I) (XIV-
Таким образом, вторая вертикальная производная Т
ггг
аномалии сг:
тяжести в некоторой точке (начале координат) с точностью до постоянна"
множителя (1/2) равна учетверенному значению аномалии силы тяжести в с
-
точке минус аномалии силы тяжести в вершинах квадратов.
§ 89. РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ
ГРАВИМЕТРИЧЕСКОЙ РАЗВЕДКИ
Как уже говорилось выше, нахождение путем вычислений значений ну
малий силы тяжести или значений вторых производных возмущающего пот» -
циала от находящегося в недрах Земли тела любой формы и с любым распре.
-
лением плотности в нем для точек, расположенных на земной поверхност
носит название прямой задачи гравиметрической разведки.
При этом поверхность Земли принимается за плоскость, а оси коордиг
принято располагать следующим образом: оси х и у помещаются в плоско!:
горизонта, а ось г направляется вертикально вниз.
Прямая задача, в противоположность обратной, всегда имеет однозначн'
решение, получение которого не связано с какими-либо принципиальны:
трудностями. Однако математические вычисления, которые необходимо п;
этом производить, отличаются большой сложностью. Сложность эта связг.
с тем, что всякое аномальное тело является трехмерным и потому при оп;
делении параметров гравитационного поля приходится выполнять трехкратн-
интегрирование, что и приводит при сложной форме тела к чрезвычайно громо;
ким выражениям. Вследствие этого в гравиметрической разведке нашли шп'
кое применение так называемые двухмерные тела, определение гравиметри-
ских характеристик которых значительно проще, чем трехмерных.
Под двухмерным телом понимается тело бесконечного простирания в однг
направлении. Форма двухмерных тел целиком определяется формой их пои
речного сечения. Двухмерное тело можно определить как цилиндрическ
полученное при движении обра&ующей по контуру поперечного сечек:
В том случае, если контур имеет форму многоугольника, мы получим прпг'
тическое двухмерное тело. Горизонтальный однородный круглый цилинд
притяжение которого равно притяжению эквивалентной массы, расположена
по оси цилиндра в форме материальной линии, является простейшим случг
-
двухмерных цилиндрических тел.
Погрешности, вызванные заменой трехмерных тел двухмерными, обыч>
невелики и для вытянутых по простиранию геологических тел, длина котор:
в 5 раз и более превосходит их поперечник, можно считать, что гравитационг-
поле над серединой их такое же, как если бы эти тела простирались в бесконе
-
ность.
Только для очень ограниченного числа тел, имеющих простейшую форм~
удается получить удобные для практического использования формулы. Конечк
подобные тела в природе встречаются очень редко. Обычно формулами для т-.
простой геометрической формы пользуются лишь для первоначальной прпбгг
зительной оценки основных параметров тела, после чего переходят к постеш
ному подбору таких параметров, которые наилучшим образом соответствов;
396.

бы данным, полученным из наблюдений. Этот подбор ведется при помощи
методов численного интегрирования.
Для расчета кривых аномалий силы тяжести, обусловленных простейшими
по своей форме телами, применяются формулы:
а) цилиндрическое кольцо
А^ - 2л/
Аб
[/1\ + Я* - \/+ 1Р 4-
1
к+1
- 1
к
],
что следует из (VI 1.12) при п = 1;
б) цилиндр
Аг = 2*/АбЯ(1-4-);
в) горизонтальный бесконечный слой
Д^ = 2я/Лб#;
г) конус
А^ = 2я/АбЯ(1 — зт I),
где угол I определяется как г = агс Н/а.
Во всех этих формулах под Аб понимается аномальная плотность Дб =
= б
2
— б-р где б
2
— плотность данного тела; б
х
— плотность окружающих
данное тело пород.
Чтобы решить прямую задачу для тел, имеющих простую геометрическую
форму, воспользуемся формулами для потенциала притяжения точки и его
производных.
Потенциал материальной точки с массой йт в соответствии с (1.15) будет
7 = (ХГОО)
где г определяется по формуле (1.5). Первые производные потенциала в соот-
ветствии (1.16) будут
• ^
=
= = Йт. (XIV. 11)
дх
1
г
3
с*у
1
гЗ да
1
/3 \ >
При вычислении вторых производных потенциала будем учитывать, что
дг х—с, дг у—дг 2—5
дх г ' ду г ' Зг г
Следовательно,
д^У д ( дУ \ х — | дг , , Дт (х—, Ат
I дУ \ х — I дг , , (1т „, (х—|)г ,
дх% дх \ дх } ' г
4
дх -г з '
1
г
я
92V д / дУ \
п
, у
—Г1
дг , , (1т „, (и—Г))2 , ,
(
1т
ду* ду \ ду ) ' г* ду ' г» гб ' гз
Получим
^ = ••= 3/ Л*. (Х1У.12)
397
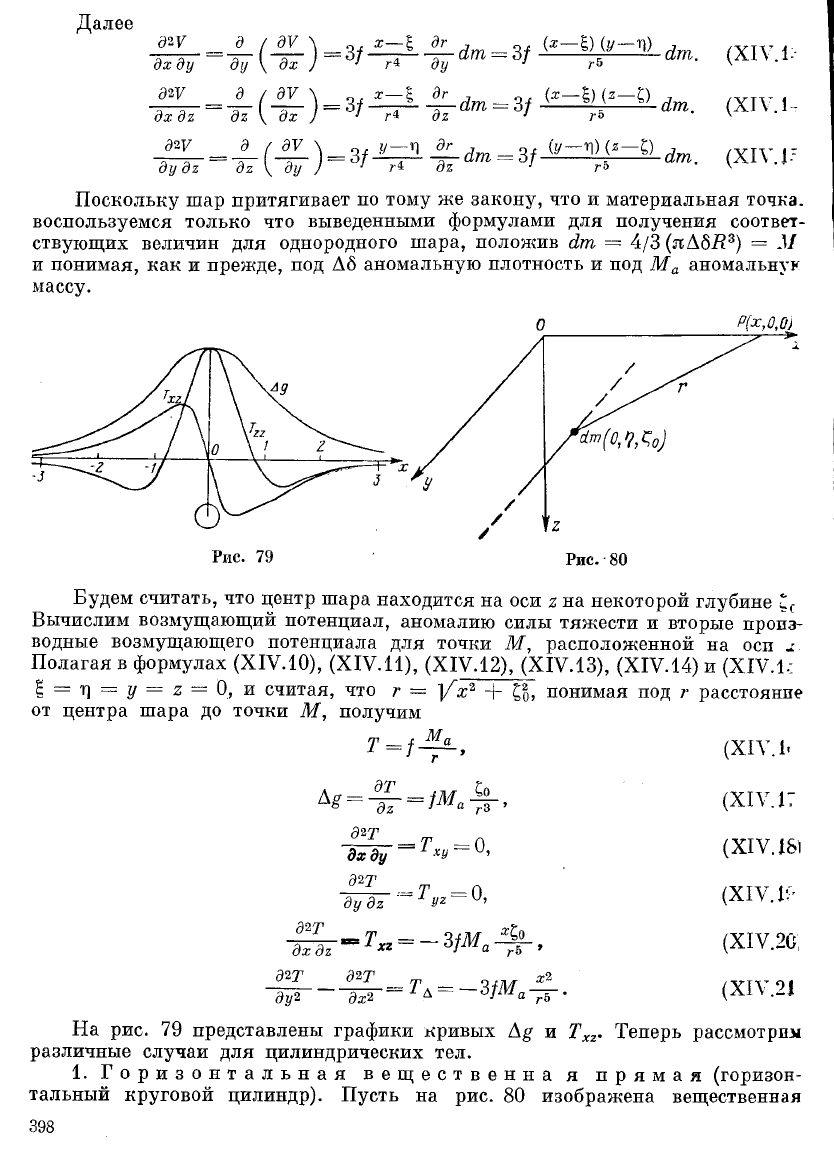
Далее
= (XIV,
1:
(XIV,-
Поскольку шар притягивает по тому же закону, что и материальная точка,
воспользуемся только что выведенными формулами для получения соответ-
ствующих величин для однородного шара, положив Лт = 4/3 (яАбД
3
) = М
и понимая, как и прежде, под Дб аномальную плотность и под М
а
аномальнук
массу.
О Р(х,0,0)
Будем считать, что центр шара находится на оси 2 на некоторой глубине
Вычислим возмущающий потенциал, аномалию силы тяжести и вторые произ-
водные возмущающего потенциала для точки М, расположенной на осп +
Полагая в формулах (ХГУ.10), (ХГУ.11), (Х1У.12), (Х1У.13), (ХГУ.14) и (XIV.!.:
^ = т] = г/ = 2 = 0, и считая, что г = ]/ж
2
+ понимая под г расстояние
от центра шара до точки М, получим
__ зт
дхду
д2 Т
ду дг.
, М
а
~
Т
Г '
(XIV.
1-
(XIV.
17
=
Т
ху = 0,
(XIV.
181
(XIV. V?
(Х1У.2С,
(Х1У.21
дх дг
х
дчт д*Т
ду2 дх*
На рис. 79 представлены графики кривых Д^ и Т
хг
. Теперь рассмотрим
различные случаи для цилиндрических тел.
1. Горизонтальная вещественна я прямая (горизон-
тальный круговой цилиндр). Пусть на рис. 80 изображена вещественная
398.

горизонтальная линия, лежащая в плоскости уг на глубине Обозначим
линейную плотность через Я, так что
с1т
= Я Расстояние от элементарной
массы йт до точки Р
г = Т/^ + л' +
^о
2
-
Используя формулу (XIV.И), получим
^ д
г
-/? ^^ /я: ?' ^
Обозначим постоянную величину х
2
+ ^о через с
2
. Представим последний:
интеграл в виде
Г
3 дз '
где
К = 1/У+с
2
.
Отсюда получаем =
-г|с?т]/Т/
г
г/
2
—|-
с
2
. Поскольку Я' = т1/1/т]
2
+ с
2
=
= "П/Д, имеем
ЯЯ' =
г|,
(XIV.22),
= Л' йт). (XIV. 23).
Дифференцируем (Х1У.22)
ЯйЯ' + Я' йЯ =
<1ц
ч
Отсюда с учетом соотношения (XIV.23) будем иметь
<1П' йт)
На основании равенства
учитывая (Х1У.22), получим
1-й'
2
Я
Я
2
— г\
2
= с
2
,
1 1—Я'
2
Д2
С
2
(XIV.25).
Таким образом,, подынтегральное выражение с учетом (XIV.24) и (XIV.2.5)?
можно представить как
ЛИ^ЛI
л»
_
д ' дг
в
С
2 •
Тогда
с ^
1
ин'~
я
'
п
О Я3
С
а
С
2 -
с2
|Л^)172 '
Таким образом,
399 >
