Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

— спутниковый геометрический, в котором ИСЗ рассматриваются как

подвижные пункты геодезического построения без привлечения какой-либо

теории движения спутника;

— спутниковый динамический, в котором используется теория движения

ИСЗ в гравитационном поле Земли;

— использование данных слежения далеких космических объектов (кос-

мических аппаратов и Луны).

Применение спутникового геометрического метода позволило за короткий

срок создать геодезические построения с расстояниями между пунктами в не-

сколько тысяч километров и установить связь между разными геодезическими

системами.

Спутниковый динамический метод позволяет определять параметры, харак-

теризующие внешнее гравитационное поле Земли, и создавать геодезические

построения в единой системе координат с началом в центре масс Земли.

Для геодезистов представляет большой интерес еще одна возможность

спутникового метода — прямое определение фигуры геоида па морях и океанах

путем измерения расстояния до поверхности воды с помощью альтиметра со

спутника, орбита которого известна [4]. Результаты слежения космических

аппаратов (КА) позволяют уточнить принятые геоцентрические координаты

станций слежения, положения полюсов и значение геоцентрической гравита-

ционной постоянной [5]. Космические методы дают возможность получить

представление о характере дрейфа континентов и вековых перемещений

полюсов Земли.

Развитие исследований Луны, Венеры, Марса и других планет с помощью

космических аппаратов привело к появлению новых ветвей геодезии, которые

иногда называют «селенодезией» и «планетодезией».

Все это позволяет утверждать, что геодезические науки в настоящее время

переживают подлинные революционные изменения, которые, несомненно,

в будущем повлияют как на постановку основных задач геодезии, так и на ме-

тоды их решения.

Глава I

ПОТЕНЦИАЛЫ ТЯГОТЕНИЯ

§ 1. СИЛОВОЕ ПОЛЕ ТЯГОТЕНИЯ

Полем некоторой величины называется область, каждой точке которой

отнесено определенное значение этой величины, причем обычно это значение

изменяется от точки к точке непрерывно. Поле может быть стационарным

(установившимся), если в каждой точке пространства оно не меняется с тече-

нием времени, или нестационарным (неустановившимся), если такое изменение

имеет место.

Поле может быть скалярным или векторным в зависимости от характера

исследуемой величины. В качестве примера скалярного поля можно привести

поле температур или поле плотностей. Характерными физическими примерами

векторных полей являются поле скоростей, поле электрической напряженности,

поле сил и т. д. В зависимости от характера действующей силы различают поля:

электростатические, магнитные, тяготения и др.

Знание свойств силового поля тяготения является необходимым для реше-

ния многих вопросов астрономии и геофизики, в частности для определения

формы космических тел.

Как известно, тяготение (или притяжение) является неотъемлемым свой-

ством материи. Закон взаимодействия между отдельными материальными части-

цами был установлен Ньютоном и получил наименование закона всемирного

тяготения. Этот закон обычно формулируется так: две «частицы» с массами т

н т' взаимно притягиваются с силой, пропорциональной произведению этих

масс и обратно пропорциональной квадрату расстояния между ними. Под

«частицей» здесь подразумеваются тела, размерами которых можно пренебречь

по сравнению с расстояниями между ними, т. е. так называемые материальные

точки. Если под г понимать расстояние между частицами с массами т и т',

а под Р — величину силы притяжения, то закон Ньютона может быть записан

в следующем виде:

Р = (1.1)

Коэффициент пропорциональности / называется гравитационной постоян-

ной, численная величина которой не зависит ни от физических, ни от хими-

ческих свойств масс т и т', ни от величины и направления скорости их дви-

жений (при условии, что величины скоростей не приближаются к скорости

света), ни от свойств и степени заполнения среды, разделяющей эти массы.

Значение этой постоянной определяется только выбранными единицами массы,

длины и времени.

В системе СС5 / = (6,673±0,003)

•

10"

дн-см

-г"

или

см

•

г"

•

сек"

, в Ме-

ждународной системе единиц / = (6,673 ±0,003)-Ю

-11

н-м

-кг~

или м

X кг

-1

•

сек"

. Наиболее точное значение гравитационной постоянной получено

из лабораторных измерений силы притяжения между двумя известными мас-

сами с помощью крутильных весов.

При вычислении орбит небесных тел (например, спутников) относительно

Земли используется геоцентрическая гравитационная постоянная, равная

произведению гравитационной постоянной на массу Земли (включая ее атмо-

сферу)

/М = (3,98603 ± 0,00003)

•

сек"

Это значение геоцентрической гравитационной постоянной соответствует

системе фундаментальных астрономических постоянных, принятой в 1964 г.

на съезде Международного астрономического союза.

Сила взаимного притяжения материальных частиц в соответствии с зако-

ном Ньютона (1.1) является функцией только координат взаимодействующих

частиц. Формула (1.1) включает в себя предположение о мгновенности рас-

пространения взаимодействий. Однако опыт показывает, что мгновенных вза-

имодействий в природе не существует. Поэтому и классическая механика,

исходящая из представлений о мгновенности распространения взаимодействий,

заключает в себе некоторую неточность.

Влияние конечности скорости распространения взаимодействий на дви-

жение учитывается релятивистской механикой, основанной на принципе отно-

сительности Эйнштейна.

Скорость распространения взаимодействий можно назвать универсальной

постоянной, являющейся одновременно скоростью распространения света

в пустоте. Ее численное значение равно С = 2,99793 -10

см/сек.

Однако на практике достаточно точной оказывается классическая меха-

ника. Скорости, с которыми приходится иметь дело в космической геодезии,

часто настолько малы по сравнению со скоростью света, что предположение

о бесконечности последней практически не влияет на точность результатов.

Поэтому в дальнейшем мы будем исходить из положения классической или

ньютоновской механики и не учитывать поправок, вытекающих из принципа

относительности Эйнштейна.

Определение силы взаимного притяжения двух тел, находящихся на рас-

стоянии, сравнимом с их размерами, является чрезвычайно трудной задачей.

Любые две точки, находящиеся внутри этих тел, притягивают друг друга со-

гласно закону Ньютона, но сила взаимного притяжения самих тел опреде-

ляется значительно более сложным образом. Величина этой силы и ее направле-

ние зависят как от строения притягивающих тел, так и от их внешней формы.

Силовое поле тяготения некоторой материальной массы определяется

ускорением в каждой точке пространства, т. е. силой, действующей на еди-

ничную массу, помещенную в эту точку. Поскольку сила в этом случае численно

равна ускорению, при дальнейшем изложении не будем различать эти

два понятия.

Следовательно, силовое поле будет известно в том случае, если в каждой

произвольной точке пространства можно найти ускорение Р (величина уско-

рения определяется формулой (1.1), положив в ней

тп'

= 1).

Ускорение Р является вектором, имеющим величину Р и напра-

вление.

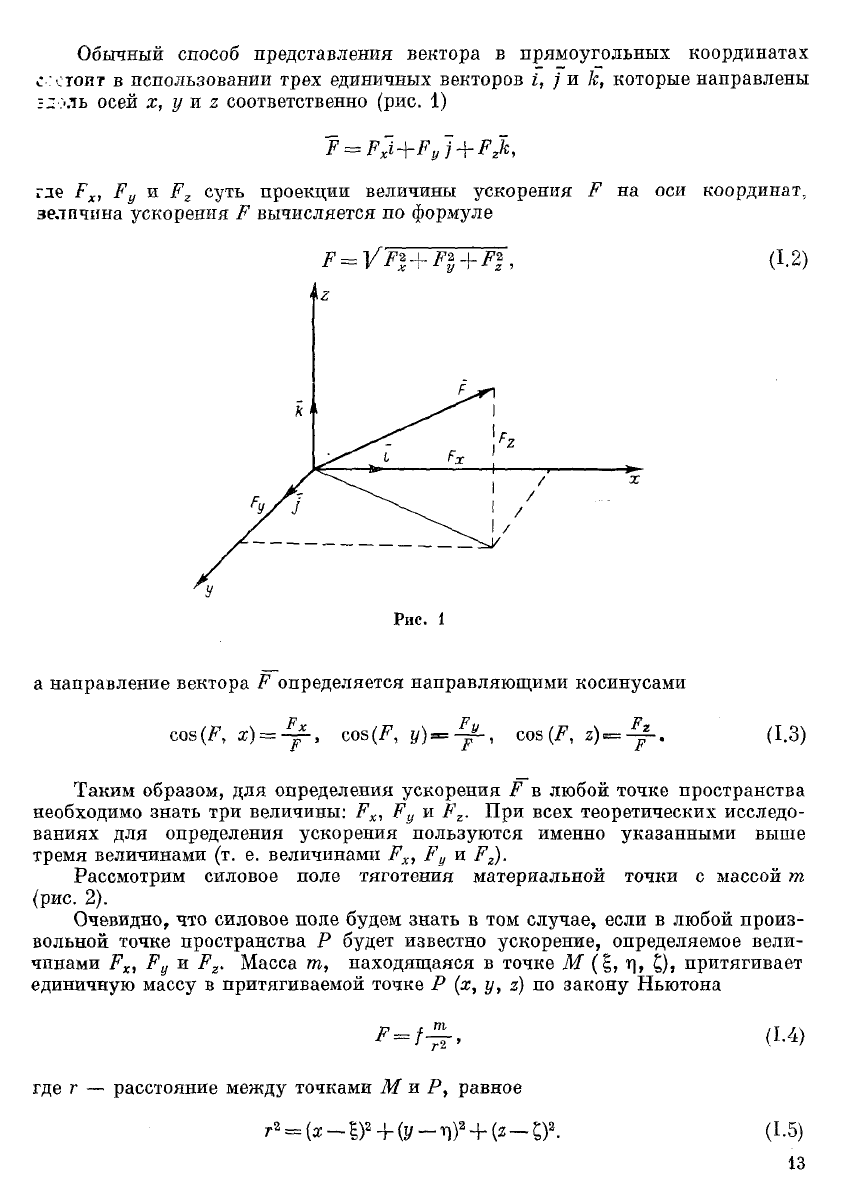
Обычный способ представления вектора в прямоугольных координатах

стоит в использовании трех единичных векторов г, ] и к, которые направлены

злоль осей х, у

г соответственно (рис. 1)

Р^Р~1+Р

] + Р

к,

где Р

, Р

и Р

суть проекции величины ускорения Р на оси координат,

зелпчина ускорения Р вычисляется по формуле

а направление вектора Р определяется направляющими косинусами

С08

(Р, я) = соВ(Р, 2/)=^,

СОВ

(Л

= ^-. (1.3)

Таким образом, для определения ускорения Р в любой точке пространства

необходимо знать три величины: Р

, Р

и Р

. При всех теоретических исследо-

ваниях для определения ускорения пользуются именно указанными выше

тремя величинами (т. е. величинами Р

, Р

и Р

Рассмотрим силовое поле тяготения материальной точки с массой т

(рис. 2).

Очевидно, что силовое поле будем знать в том случае, если в любой произ-

вольной точке пространства Р будет известно ускорение, определяемое вели-

чинами Р

, Р

и Р

. Масса т, находящаяся в точке М т], С), притягивает

единичную массу в притягиваемой точке Р (х, у, г) по закону Ньютона

*О Л)

где г — расстояние между точками М и Р, равное

=Ф - Е)

-НУ --п)

+ (

(1.5)

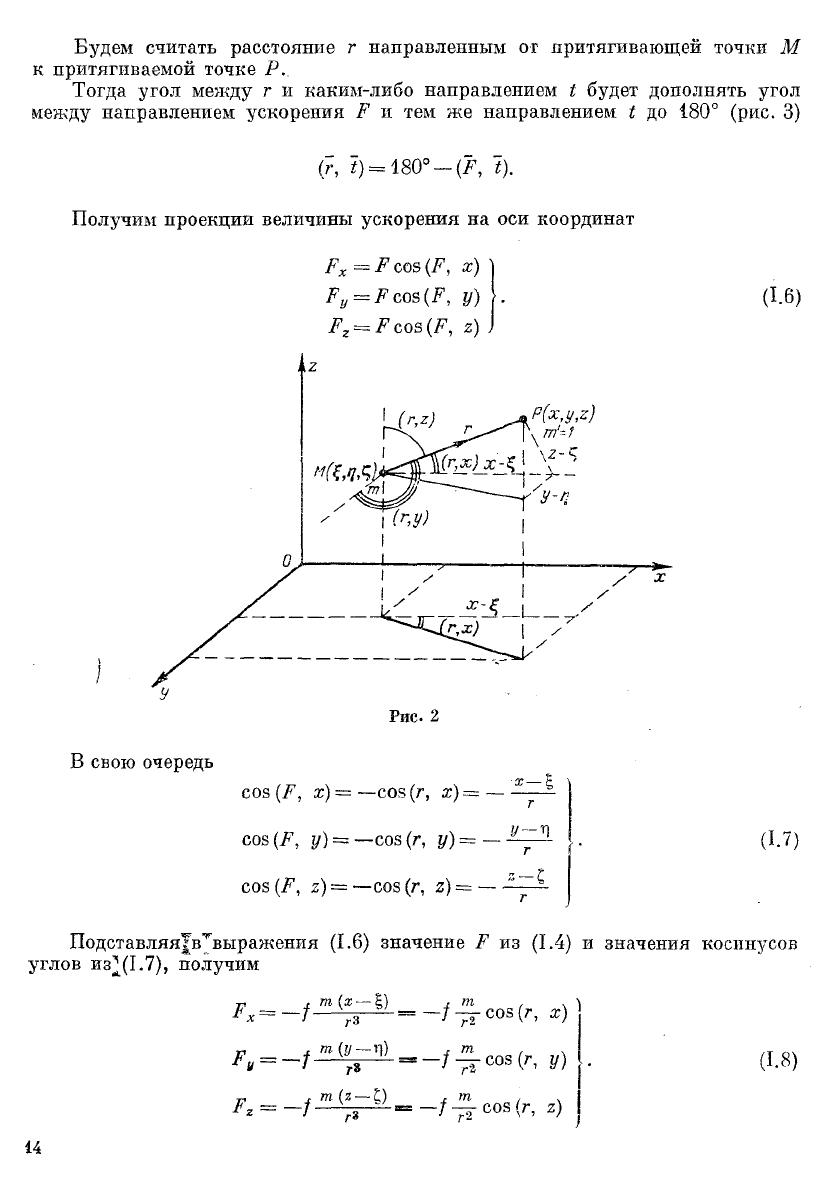
Будем считать расстояние г направленным от притягивающей точки М

к притягиваемой точке Р.

Тогда угол между г и каким-либо направлением I будет дополнять угол

между направлением ускорения Р и тем же направлением I до 180° (рис. 3)

(г, 0 = 180°-(Р, I).

Получим проекции величины ускорения на оси координат

=Рсо5(Р, х)

= Рсоа(Р, у)

= Рс08(Р, 2)

Р(х,у,г)

Рис. 2

В свою очередь

соз (Р, х) = —соз (г, х) = —

соз (Р, у) = —соз (г, у)= —

соз (Р, г) = —соз (г, г) = —

X— §

У — Т)

(1.6)

(1.7)

Под став ляяТв^выражения (1.6) значение Р из (1.4) и значения косинусов

углов из2(1.7), получим

т(х —

•1)

гЗ

р —

т(у~

•11)

г»

Рг =

т (г —

С)

Рг =

Г8

/т5-соз(г, х)

т.

75"

Та"

(1.8)

В случае силового поля нескольких отдельных точек, для каждой из них

могут быть написаны выражения (1.8). Компоненты ускорения по осям коорди-

нат СЛОЖИМ II ПОЛуЧИМ

к=1

Рг =

ти (у—

•Цк)

гЗ

(г-

-1к)

к-1

(1.9)

Рассмотрим теперь случай силового поля материального тела произвольной

формы. Обозначим через (1пг элементарную массу, которую будем рассматри-

вать как точечную. На основании выражений (1.8) компоненты элементарной

Рис. 3

силы, с которой элементарная масса дт притягивает точечную массу т! = 1,

будут равны

д,т

= — / 4?- соз (г, х),

гз

Г 2

йт

ар,. = — = — /-2.соз (г, г/),

= —/ ^—Апг = — / соз (г, г).

Г2

Интегрируя по объему тела т, получим составляющие силы притяжения Т

для материального тела

соз (г, г)

Г2

соз (г,

у)

/•2

соз (г,

(1.10)

Под г здесь понимается расстояние от любой текущей точки М (текущая

точка берется там, где имеются притягивающие массы: либо внутри данного

тела, либо на его поверхности) до притягиваемой точки Р и является перемен-

ной величиной. Интегрирование производится по объему т (по координатам

текущей точкп М — т) и координаты притягиваемой точки Р — х, у,

т,

рассматриваются как параметры.

Если известно направление, по которому данное тело притягивает точку Р,

то, естественно, в таком случае одну из координатных осей, например ось 2,

совместить с направлением действующей силы Р. Тогда проекции силы Р,

на оси х и у будут равны нулю, а

= (1.11)

В заключение рассмотрим силовое поле, создаваемое массами, распре-

деленными в виде бесконечно тонкого слоя на некоторой поверхности ст. Ана-

логично предыдущему можно доказать, что

'И

^- . (1.12)

Интегрирование здесь производится по поверхности ст, г — расстояние

от текущей точки М (находящейся на поверхности ст) до притягиваемой точки Р,

координаты которой х, у иг по-прежнему рассматриваются как параметры.

Если ось г совместить с направлением действующей силы, то, очевидно,

= Ру = 0, а

= Р = (1.13)

§ 2. ПОНЯТИЕ О ПОТЕНЦИАЛЕ. ОСНОВНЫЕ ВИДЫ

ПОТЕНЦИАЛОВ СИЛЫ ТЯГОТЕНИЯ

Формулы (1.8), (1.9) и (1.10), служащие для вычисления проекций силы

притяжения на оси координат, однотипны и могут быть получены как частные

производные одной скалярной функции, получившей название потенциала.

Введение этого понятия значительно облегчает изучение силовых полей тяго-

тения, так как вместо изучения трех функций независимых переменных х, у

и 2\ Р

, Ру, Р

можно ограничиться изучением только одной функции — по-

тенциала.

Потенциалом называется функция, частные производные которой по осям

координат равны проекциям действующей силы на соответствующие оси.

Если Р

, Ру и Р

— проекции силы тяготения на оси координат, то потен-

циал (потенциальная функция) этой силы, согласно определению, должен

удовлетворять следующим условиям:

-й--'. Я-'.. <'•">

Учитывая эти связи между потенциалом V и составляющими силы тяготе-

ния, можно сказать, что потенциал полностью характеризует силовое поле.

Найти же составляющие притяжения по формулам (1.14) значительно проще,

чем по формулам (1.10).

Определим потенциал V (х, у, г) силы тяготения для различных силовых

•олей.

Докажем, что потенциал точечной массы т (см. рис. 2) определяется фор-

мулой

У(Х, у, 2) = /-^. (1.15)

Доказательство заключается в проверке: будет ли удовлетворять данная

функция условиям (1.14). Возьмем частные производные от функции V (х, у, г)

по переменным х, у, г. Получим

дУ _ дУ дг _ т дг

дх дг дх * г2 дх

и аналогично по другим переменным у

г. Но из формулы (1.5) следует, что

дг х —

дг у— Г] дг %—^

Следовательно,

дх

' ду

дУ __ ,

дх '

ду '

дУ ,

дъ ~ '

(X-

г 3

(у-

•т))

(2-

дг

(1.16)

Сравнивая полученные формулы с формулами (1.8), убеждаемся в том, что

действительно функция V (х, у, г) = / (т/г) является согласно определению

потенциалом точечной массы т.

В том случае, когда силовое поле создается несколькими точечными мас-

сами т

т., . . ., т,. потенциал будет иметь вид

и*, у, г) = /2'

А-1

ти

Гк

(1.17)

В самом деле, если продифференцировать (1.17) по переменным х, у иг,

то получим выражения (1.9). Заметим, что выражение (1.17) теряет смысл, когда

точка Р сливается с одной из притягивающих точек (тогда 1/г -> оо).

Точечный потенциал есть конечная и непрерывная функция координат

притягиваемой точки Р, если только притягиваемая точка не совпадает ни

с одной из притягивающих масс; то же самое справедливо и для производных

от V (х, у, г) по координатам точки Р.

Формула (1.17) иллюстрирует одну важную особенность потенциала —

скалярностъ, т. е. потенциал равнодействующей силы равен арифметической

сумме потенциалов ее составляющих.

Пользуясь этой особенностью потенциала, при определении потенциала

силы тяготения материального тела поступим следующим образом. Разобьем

притягивающую массу на бесконечно большое число элементарных масс йт,

которые будем рассматривать как точечные массы. Положим, что масса Ит

занимает элементарный объем д,х = й^ацй^,. Воспользуемся понятием объемной

плотности

йт

(1.18)

ЙТ

2 Заказ 1379

595387

Чври!г!веька державна

••пасна

615Л10ТЕКА

> • в. Г. КОРРПЕНКА

понимая под объемной плотностью отношение бесконечно малой массы йт

к занимаемому ею объему й%. Очевидно, что

йт = 8йх. (1.19)

Потенциал элементарной массы в точке Р (х, у, г) будет

йУ(х, у, г) =

где г — расстояние между элементарной массой и точкой Р.

Проинтегрировав по объему т, занимаемому притягивающей массой, полу-

чим значение потенциала тела в точке Р

У(х, у, = (1.20)

Для проверки покажем, что производные от полученной функции V (х, у, г)

будут равны проекциям силы притяжения на оси координат. Поскольку ин-

тегрирование производится по переменным т], а величины х, у, г играют

роль параметров, будем иметь

-е-мН'ДД"*""*.

Но

(I)

1 дг 1 х —

1 .

- =— -5"

СОЗ (Г,

X).

Поэтому

дх /"2 дх г 2 г г-

дУ

дх

Ш *=Ш * №

и аналогично для производных по двум другим координатам. Таким образом,

убеждаемся, что и в данном случае удовлетворяются условия (1.14), т. е. что

функция V (х, у, г) действительно является потенциальной.

Для определения потенциала какого-либо тела требуется знать точную

форму поверхности, ограничивающей данное тело (поскольку пределы интег-

рирования зависят от формы притягивающего тела), и плотность в каждой точке

как внутри тела, так и на его поверхности.

Рассмотрим еще два вида потенциалов силы тяготения: потенциал про-

стого слоя и потенциал двойного слоя. Простым слоем называются массы, рас-

пределенные на некоторой поверхности а в виде бесконечно тонкого слоя,

иначе говоря, массы, сконденсированные на этой поверхности.

Понятие простого слоя имеет реальное значение в электростатике, где

заряды леяеат бесконечно тонким слоем на поверхности кондуктора, причем

на единицу поверхности приходится количество электричества (х.

Понятие двойного слоя обязано своим происхождением учению о магне-

тизме, поскольку элементарный магнит является не точечной массой, а так

называемым диполем, т. е. бесконечно малой иглой, на концах которой сосре-

доточены равные по величине положительное и отрицательное количества

магнетизма.

В теории фигуры Земли потенциал простого слоя, как и потенциал двой-

ного слоя, имеет важное значение, поскольку потенциал объемных масс вне

тела может быть представлен либо в виде одного из этих потенциалов, либо

в виде определенной комбинации потенциалов простого и двойного слоев,

распределенных на поверхности тела.

Эта замена приводит к значительным упрощениям, так как в этом случае

интегрирование будет производиться не по объему, а по поверхности.

Для вывода формулы потенциала простого слоя поступим следующим

образом. Допустим, что в объеме х, заключенном между двумя очень близкими

поверхностями о и а' (рис. 4), находятся притягивающие массы с объемной

плотностью б. Тогда потенциал объемных масс будет представлен формулой

X X

где интегрирование распространяется на весь объем т, а под г понимается рас-

стояние от текущей точки М г|, до притягиваемой точки Р (х, у, г).

Р(х,у,г)

т'-1

Рис. 4

Если к — расстояние по нормали между поверхностями а и а' достаточно

мало, то с точностью до малых высших порядков элементарный объем йх можно

представить как

йт —

йак,

где — элемент поверхности ст, а элементарную массу йт, как

йт = б

йа.

(1.22)

Тогда приближенно потенциал притягивающих масс можно представить

к виде

У(Х, у, =

где г — расстояние от элемента йа поверхности о до точки Р.

Будем неограниченно приближать поверхность о' к поверхности о, тогда

-*•

0, но при этом приближении будем оставлять неизменной массу йт внутри

каждого элементарного объема йх. Поставим условие, чтобы

Пт б/г =|л.

к-* О

(1.23)