Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

или, окончательно

(П.35)

Следовательно, функция V может быть найдена в любой точке Р внешнего

пространства по тем значениям, которые принимает на поверхности а линейная

комбинация аУ +

<1У/с1п.

Вся трудность задачи заключается в том, чтобы

построить для данной поверхности а функцию Е.

В заключение параграфа докажем, что внешняя задача Дирихле имеет

единственное решение. Предположим обратное, а именно, пусть имеются две

функции V и V, гармонические вне о, регулярные на бесконечности и при-

нимающие на поверхности о одинаковые значения. Тогда новая функция Т =

— у — у будет гармонической вне о и регулярной на бесконечности. При-

меним к ней (II. 7), положив II = У = Т

т о

Ио по условию во внешнем пространстве АТ = 0, а на поверхности Т — О,

поэтому получим

" Б {Т, Т)йт = 0.

Это равенство возможно лишь в том случае, когда в каждой точке внешнего

пространства

ОТ

дх

дТ

ду дг

Отсюда следует, что функция Т должна сохранять постоянное значение

во всем внешнем пространстве. Но на бесконечности функция Т должна обра-

щаться в нуль, следовательно, в каждой точке внешнего пространства функция

Т = 0. Таким образом доказано, что внешняя задача Дирихле имеет единствен-

ное решение. Аналогично доказывается единственность решения внешней

задачи Неймана.

§ 12. ЗАДАЧИ ДИРИХЛЕ ДЛЯ СФЕРЫ

И БЕСКОНЕЧНОЙ ПЛОСКОСТИ

Приведем решение внешней задачи Дирихле для поверхности сферы. Пусть

заданная поверхность а есть сфера радиуса В с центром в 0 (рис. 19). Определим

в произвольной точке внешнего простран-

ства Р (р, 0, А.) функцию У

, гармоническую

вне данной поверхности сферы а, регуляр-

ную на бесконечности и принимающую на

поверхности сг заданную совокупность зна-

чений Нт У

= / (0', %'). Здесь р, 0, X —

значение сферических координат точки (без

штрихов — во внешнем пространстве, со

штрихами — на поверхности сферы).

Определим функцию Грина для сферы.

Для этого на прямой ОР на расстоянии р'

отметим точку Р' под условием, чтобы

Рис. 19 рр' = В

. Точки Р и Р' называются сопря-

Р(РА*)

м(в\я')

женными. Возьмем во внешнем относительно сферы а пространстве перемен-

ную точку К и определим ее расстояния до сопряженных точек

= й

+ Р

—2йр созф

г'

= й

4-р'

— 2 йр' СОЗ

На поверхности сферы получаем очевидные соотношения

г! = В

+ р

— 2Вр соз

г|з

г'

= П* + р'

-2Кр' соз

(11.36)

(П.37)

гг, , Я*

1ак как р = то получим

= В

+- 2 С034 = ^ (Р

+ Я

- 2Вр соз Ф) = г?,

отсюда г'

= (В/р) г

Функция Грина С, входящая в формулу (И.33), для случая сферы имеет вид

(11.38)

г г р

1 1?

Действительно, функция [7 = — — — будет удовлетворять условию регу-

лярности на бесконечности и будет гармонической во всем внешнем простран-

етве, функция — будет регулярной на бесконечности и гармонической во всем

внешнем пространстве, кроме самой точки Р. Кроме того, на поверхности сферы:

1_ р 1 д

~~ Г

г'^Р г

Я г

р ~ •

Таким образом, функция С удовлетворяет всем условиям, которым должна

удовлетворять функция Грина.

Вычислим нормальную производную

йС 1 йг . Я 1 йг' ,ут оп\.

г2 йп т" р йге

•

^ • '

Здесь п — направление внешней нормали, совпадающее с направлением й

Дифференцируя выражения (11.36), получим

г —д, — р создЬ,

йп !

г' -^- = й-р'созаЬ.

йп

Подставляя эти значения в (11.39), получим

АС й — рсозг|) , Н й—•р'соз'ф

йп гЗ "т р

На самой сфере нормальная производная функции Грина принимает вид

Д2

г йв\ _ Д-рсо8т|> . Д —со

I ап )с г! р дз

После сокращения и приведения подобных, получим окончательно

р2

—Д2

(—) -

\ йп /о

я,! • (

°)

Подставив (11.40) в (11.33), получим решение внешней задачи Дирихле

в виде

= (И.41)

Эта формула называется интегралом Пуассона для внешнего пространства.

Аналогично можно доказать, что внутренняя задача Дирихле имеет ре-

шение

(р, 6, = 9', т. (11.42)

Получив интегралы Пуассона для точек внешнего и внутреннего про-

странства, необходимо доказать два положения: 1) определяемые функции У

и У

-, рассматриваемые как функции координат х, у, г, действительно удовлет-

воряют уравнению Лапласа, 2) при стремлении точки Р к любой точке сферы

определяемая гармоническая функция стремится именно к тому значению,

которое задано для этой точки сферы, т. е. что соблюдаются условия

НтУДр, 9, X) = Нт У

(р, 9, л) = /(0', X'). (11.43)

р->-н р->-Н

При доказательстве первого положения заметим, что функции У

и У,- будут

гармоническими функциями координат точки Р в том случае, если каждый

элемент интегралов (11.41) и (11.42) будет обладать этим свойством. Чтобы

убедиться в этом, необходимо доказать, что функция (Н

— р

)/г

, называемая

ядром интеграла Пуассона, будет гармонической функцией координат х, у, г.

Для этого представим ядро интеграла Пуассона в виде суммы двух гармони-

ческих функций.

Преобразование ядра интеграла проведем следующим образом.

Из соотношения (11.37) можно получить

—

— 2В

+ 2В р соз

г|з.

Следовательно,

р2 —Д2 1 2Д

Из формулы (11.37) следует

дг я — р С05 1]}

дя т

ж потому

р2 — Д2 1 2Д дг

з ~~

/-2 дЯ '

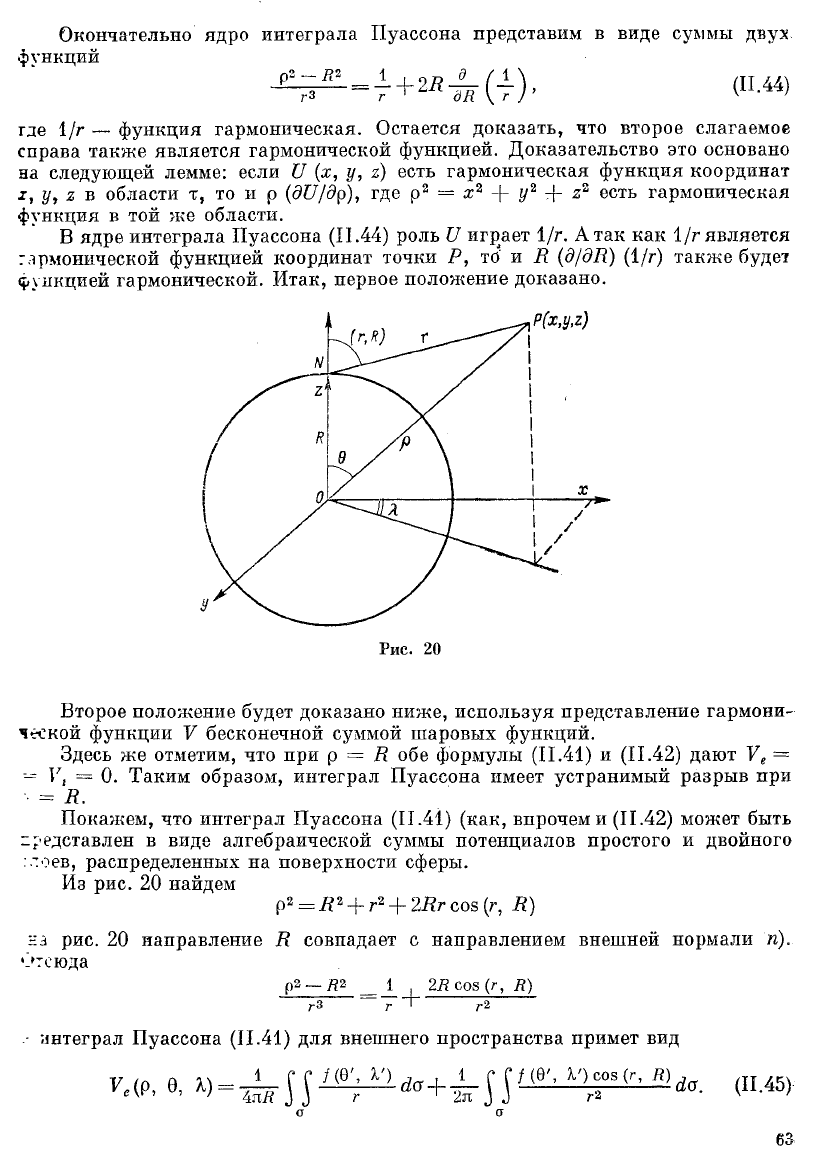
Окончательно ядро интеграла Пуассона представим в виде суммы двух

функций

-^-т+и-ягСт)- ("•«)

где 1/г — функция гармоническая. Остается доказать, что второе слагаемое

справа также является гармонической функцией. Доказательство это основано

на следующей лемме: если 11 (х, у, 2) есть гармоническая функция координат

I, у, г в области т, то и р (д(7/др), где р

= х

+ г/

+ г

есть гармоническая

функция в той же области.

В ядре интеграла Пуассона (11.44) роль II играет 1/г. Атак как 1/г является

гармонической функцией координат точки Р, тб и К (д/дВ) (1/г) также будет

функцией гармонической. Итак, первое положение доказано.

Второе положение будет доказано ниже, используя представление гармони-

ческой функции V бесконечной суммой шаровых функций.

Здесь же отметим, что при р = В обе формулы (11.41) и (11.42) дают У

— V, = 0. Таким образом, интеграл Пуассона имеет устранимый разрыв при

= В.

Покажем, что интеграл Пуассона (11.41) (как, впрочем и (11.42) может быть

представлен в виде алгебраической суммы потенциалов простого и двойного

:лоев, распределенных на поверхности сферы.

Из рис. 20 найдем

р8 = Дя + г

+ 2Дгсо8(г, В)

на рис. 20 направление К совпадает с направлением внешней нормали п).

Отсюда

р2 —Д2 __ 1 2Д С08 (г, Д)

—

г + 7-2

• интеграл Пуассона (11.41) для внешнего пространства примет вид

о о

Очевидно, что первый интеграл в (11.45) можно рассматривать в качестве

потенциала простого слоя, плотность которой

а второй интеграл является потенциалом двойного слоя плотности

Получим значение интеграла Пуассона для плоскости. Переход от сферы

к плоскости осуществляется при неограниченном возрастании радиуса сферы.

Положим в (11.41) В -»- сю. При этом Нт (р-\-В)/2В = 1. Обозначив разность

р — В через 2 (высота точки над плоскостью), получим

Здесь под о следует понимать бесконечную плоскость, а под до — элемент этой

плоскости.

(И.46)

Глава III

ШАРОВЫЕ И СФЕРИЧЕСКИЕ ФУНКЦИИ

§ 13. ОСНОВНЫЕ СВОЙСТВА ШАРОВЫХ

И СФЕРИЧЕСКИХ ФУНКЦИЙ

В теории потенциала широкое применение нашли так называемые шаровые

и сферические функции.

Шаровой функцией степени п называется целый однородный многочлен

степени п в переменных х, у, г, удовлетворяющий уравнению Лапласа. Обозна-

чим его через 8

(х, у, г). Докажем одно важное свойство однородных много-

членов: если гармоническую функцию возможно представить в виде ряда одно-

родных многочленов, то последние должны быть шаровыми функциями.

Предположим, гармоническая функция 7 представлена бесконечным рядом

однородных многочленов

оэ

^=2 $„(*, У, 2).

п=О

Так как функция V — гармоническая, то она должна удовлетворять урав-

нению Лапласа, поэтому

со

А7 = 2 &8

(х, У, 2) = 0.

п= О

Но каждый из многочленов А8

(х, у, г) представляет собой в свою оче-

редь однородный многочлен степени п — 2 (при п = 0 и п = 1 А8

(х, у, г)

тождественно равен нулю); поэтому в представленном выше ряде многочленов

никакие приведения членов между отдельными многочленами невозможны,

п потому еумма этого ряда может быть равной нулю, лишь если его члены

порознь равны нулю, откуда следует, что

Д8

(х, у, г) = О,

т. е. каждый однородный многочлен 8„ (х, у, %) должен удовлетворять уравне-

нию Лапласа, т. е. быть шаровой функцией. Впоследствии это важное свойство

однородных многочленов будет использовано для того, чтобы найти шаровые

и сферические функции в явном виде. Именно, если брать заведомо гармони-

ческую функцию и раскладывать ее в ряд однородных многочленов, то на осно-

вании доказанного выше свойства полученные однородные многочлены должны

быть шаровыми функциями.

5 Заказ 1379 65

В силу основного свойства однородных функций имеет место формул:

(х, у, г) = р?8

(±, 1-). (Ш.1

Пусть х, у, г — прямоугольные координаты внешней точки Р, а р, 9, X —

сферические координаты той же точки (см. рис. 20). Связь между прямоуголь-

ными и сферическими координатами дается формулами

р 8ХП0

соз

г/

= рзт9зтА, |> (111.1

г = рсоз9 /

где

= х

+ у

+ г

. (Ш.З

Переходя к сферическим координатам, получим

Чт 7' 7)

=у

' <

1П

Функция У

(9, X) будет однородной функцией степени п от зт 0 соз/..

31П 0 81П X и соз 9 и называется сферической функцией степени п.

Подставляя (Ш.4) в (Ш.1), получаем связь между шаровыми и сфери-

ческими функциями

(х, у, 2) = р«Г„(0, X).

Основное свойство сферических функций выражается так называемой теоремой

ортогональности. Для доказательства этой теоремы обратимся к формуле Грина

(11.18) для гармонических функций V и V, положив

17=8

(х, у, 2) = р"УД9\ X'),

У = 8

(х, у,

= р«У

(0', X').

Поверхность сг принимается за сферу, поэтому производные А8/Ап совпа-

дают с производными по направлению р

ли й8

йп йр

йУ ^ йЗ

йп йр

= пр

(9', Х%

•

шр

(9", X').

Подставляя полученные значения функций и их нормальных производных

в (11.18), получим

I ^ [р»р

тУ

(9', X') У

(0', X') - р

^пУ

(9', X') У

(0", X')] Аа = 0. (Ш.5)

На поверхности сферы сг имеем

л+т_1

= цп+т-1^

Выразим элемент поверхности Аа через элемент телесного угла

Аа>

Аа = Е

Аа>.

Очевидно Асо можно рассматривать как элемент поверхности на сфере

радиуса 1.

После сокращения в (II.5) на Е

п+т+1

получим

(т-п)^Г

(9\ Г)Г

(в% X') аа = 0. (Ш.6)

Отсюда вытекает, что, если т п, то

со

Это и есть свойство ортогональности сферических функций. Заметим,

что интеграл (9', к') йсо, который получается в левой части (Ш.6) при

со

•п

= п есть некоторая постоянная, отличная от нуля (все элементы интеграла

положительны).

§ 14. РАЗЛИЧНЫЕ ВИДЫ ШАРОВЫХ

И СФЕРИЧЕСКИХ ФУНКЦИЙ

Найдем шаровые и сферические функции в явном виде. Сначала рассмо-

трим один частный случай.

Пусть функция г является функцией только координат точки Р (см. рис. 20).

Тогда из треугольника ОЫР

2=Д2

+ р

2_2йр С08 9.

Представим функцию 1/г (гармоническую при г ф 0) в виде однородных

многочленов в переменных координатах точки Р. Очевидно, что

1 --

-1 — [Д

-Ьр

-гДрсоаЭ] 2 (III.7)

Раскладывая многочлен в ряд по степеням отношения Е/р, применительно

к "случаю, когда точка Р является внешней по отношению к сфере радиуса Е

(т. е. при р > Е), получим

пли в общем виде

1 X

А р

71=0

Р„(с°з

)- (III.8)

Аналогично, если точка Р заключена внутри сферы радиуса Е (р <5 Е), то

ПЛИ

СХ)

2-^гР„(сове). (Ш.9)

п=О

Заметим, что функции угла 0, стоящие множителями при степенях

В/р (или р/В), являются полиномами (или многочленами) Лежандра, обознача-

емыми в общем случае Р

(сов 0). В нашем случае первые из них

(

О3

= 1,

(С08 0) = СОЗ 0,

(СО8 0) = |-СО8

0 -^.

Последующие значения полиномов Лежандра можно получить при помощи

рекуррентной формулы. Приведем эту формулу без доказательства

п+1

(соз 0) = ^±1 соз 0Р„ (соз 0) - Р

_! (соз 0). (111.10)

Из формулы (111.10) заключаем, что Р

(соз 0) с четными индексами п

содержат только четные, а с нечетными индексами — только нечетные степени

переменной соз 0. Отсюда следует свойство полиномов Лежандра

(—соз 0) = (-1 )

(соз 0). (111.11)

Заметим еще, что поскольку основная переменная 0 изменяется в пределах

от 0 до л, соз 0 заключен в пределах —1 СОЗ 0=^+1. Этим определяется

в нашем случае область изменения полиномов Лежандра Р

(соз 0).

Рассмотрим произвольный член основного ряда (111.9)

(соз 0)

и докажем, что это выражение представляет собой целый однородный много-

член степени п в переменных х, у, %. В самом деле, как было замечено выше,

полином п-й степени Р

(соз 0) может заключать в себе только члены со степе-

нями (соз 0)", (соз0)"~

, (соз 0)"~

и т. д. В общем случае произвольный

член полинома Р

(соз 0) содержит переменную соз 0 в степени п — 2к, где

к = 0, 1, 2 ... п/2 при п четном 1

| I

/с = 0, 1, 2 ... —^— при п нечетном

Поэтому в (III.9) мы с точностью до постоянных множителей, являющихся

функцией только п и к, имеем дело с членами типа

р" (соз Щ

2к

= [р

2к

(соз 0)

ге

2й

]

•

2к

Но согласно (III.2) и (III.3) в прямоугольной системе координат

р соз 0 =

= а;

+г/

+ 2

Поэтому

Р"(С05 в)

= 2

-2

(х

+ у

+ 2

)

= 8

{х, у, 2),

так как это выражение при любом к может дать только члены вида х

у которых сумма показателей равна всегда п. Следовательно, выражение

(соз 0) является целым однородным многочленом степени п в перемен-

ных х, у, 2. Поскольку, кроме того, ряд (II 1.9) однородных многочленов

(соз 0) представляет собой гармоническую функцию 1/г, то, согласно дока-

занному выше, все эти многочлены должны являться шаровыми функциями.

Итак, мы установили, что р

(соз 0) есть частный вид шаровой функции

степени п, а Р

(соз 0) — полином Лежандра — частный вид сферической

функции степени п.

Шаровые функции, ряд которых представляет гармоническую функцию 1/г

(Ш.8) вне сферы, имеют отрицательный порядок

<7 , (г и -V -

п(оозв)

У, 2)

Рассмотрим частный случай, когда 0=0. Тогда при р 5> Я г = р — В,

(III. 12)

(111.13)

Сравнивая эти разложения с (Ш.8) и (III.9), приходим к выводу, что при

0 = 0 (соз 0 = +1) все многочлены Лежандра равны 1, т. е.

( 1) = 1, (111.14)

п имея в виду, что Р

(соз 0) содержит либо одни четные, либо одни нечетные

степени сое 0

Рп{—1) — (—!)"• (111.15)

Далее положим, что функция г является не только функцией координат точки

Р (р, 0, А), но и функцией координат точки М (0', А'), находящейся на сфере

радиуса В (рис. 21). В этом случае

-^-=[Д

+ р

—2Ярсозф]

. (111.16)

Значение соз ф определяется из сферического треугольника МИР

(рис. 21), образованного дугами больших кругов,

соз

г|э

= соз

соз 0' + зт

зт 0' соз (Я' —

А)

= соз 0 соз 0' + зт 0 зт 0' X

X соз

соз X' + зт 0 зт 0' зт

зт А/. (Ш. 17)

1 _ 1

г р — Н

априр К г — В — р

1 _ 1

г ' П—р

•(•-т)

0-8-)'

со

71=0

СО

•2-

Д"

П™+1

дп+г-