Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Формула (111.16) аналогична формуле (III.7), разница лишь в замене

соз 0 на соз ф. Поэтому, повторив сделанные ранее выводы, получим

п=0

Д"

рП+1

Р„(созф)(р>Д),

(111.18)

п=О

Дп+1

Л(созф)(

<я).

(III.19)

Р(х,у, г)

Выше было доказано, что р

Р (соз 0) — целый однородный гармонический

многочлен в переменных х, у, г; это же свойство должно принадлежать

и р

(соз г(;), так как эта функция

легко получается из р

(соз 0) путем

простого преобразования координат точ-

ки М, которое сводится лишь к пово-

роту осей, а это не может повлиять

на алгебраические свойства многочлена

относительно координат х, у, г точ-

ки Р.

Таким образом р

(соз ф) можно

рассматривать как шаровую функцию сте-

пени п в переменных х, у, г, а Р

(соз ф) — как сферическую функцию

координат 0 и Я. Выражение Р

(соз ф)/р"

будет являться шаровой функцией сте-

пени —п — 1.

Определим теперь явный вид шаро-

вых и сферических функций в общем

случае. Возьмем произвольную гармо-

ническую функцию У

(р, 0, К) внутри

сферы радиуса В и разложим ее в бес-

конечный ряд шаровых функций. Для этого, используя соотношение (11.44),

представим интеграл Пуассона (11.42) в виде

Разложим ядро интеграла по степеням р. Для этого используем выраже-

ние (111.19)

П+1

( С081])).

Дифференцируя его по В, получим

Следовательно,

00 СО

п=О п=О

СО

п=О

Подставляя полученное значение ядра интеграла в (III.20) и интегрируя

почленно, найдем

Мр, е, =

п= о а

Введя элемент поверхности сферы единичного радиуса йсо = и обо-

значив

Упф, = Я,') Л, (соз ф) Л», (111.21)

получим

оэ

VI (Р, е, я) = ^Л

' (

П1

-22)

п=0

Функцию У

(0, А) можно рассматривать как произвольную сферическую

функцию степени п, так как Р

(соз ф) является сферической функцией коорди-

нат 0 и Я и это свойство не может измениться при интегрировании ее по пере-

менным 0' и Я'. Поэтому члены ряда (111.22) —р

(0, к) будут являться

шаровыми функциями степени п.

Решим аналогичную задачу для гармонической функции У

(р, 0, к) вне

сферы радиуса В. Для этого в интеграл Пуассона (11.41) подставим значение

его ядра, используя (11.44),

Мы имели (111.18)

п= О

после дифференцирования получим

-йг(ТЬ2

^»<

сов

*>'

п=О

следовательно,

с»

п=0

Подставляя это выражение в (111.23) и почленно интегрируя, найдем

со

УДР, 0, = А,')Л,(С081>)ДГ,

п=О ст

вводя опять элемент поверхности сферы единичного радиуса и используя соот-

ношение (111.21), получим

оо

0П+1

(111.24)

п=О

Каждая шаровая функция этого ряда имеет отрицательную степень

(х, у, г) = .

Пределы рядов (111.22) и (111.24) при р -V Я должны быть равны значению

заданной на сфере функции

ПшУДр, 0, А) = /(0, X),

р->-В

ПтУДр, 0, А)=/(0, я).

р-*-В

В то же время, полагая (111.22) и (111.24) р Я, получим

Нт V, (р, 0, X) = V, (Я, 0, X) = 2 Уп (9- *•)

Р-УВ п=О

ПтУДр, 0,

Х)

= У

(Я, 0,

= 2 У„(в, Я).

Р-+К П=1

Следовательно, разрыв, который имеют интегралы Пуассона (11.41) и (11.42)

при р = Я, устраняется в рядах (111.22) и (111.24). На поверхности сферы о

оба ряда (111.22) и (111.24) дают

/(9, А) = 2 У

(0, Л). (111.25)

п=О

§ 15. РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНОЙ ФУНКЦИИ В РЯД

ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ

Полученную в предыдущем разделе формулу (111.25) можно рассматривать

как разложение произвольной функции / (0, X) в ряд по сферическим функ-

циям У (называемым игреками Лапласа).

Условия, которым должна удовлетворять функция / (0, X) для того, чтобы

разложение ее в бесконечный ряд сферических функций было возможно, для

всех функций, с которыми приходится иметь дело на практике, обычно выпол-

няются. Поэтому полученный результат (111.25) можно сформулировать так:

непрерывная функция двух переменных, заданная для всех точек сферы, может

быть единственным образом разложена в соответствующий ей ряд сферических

функций.

Выразим функцию У

(0, А) в явном виде. Для этого следует сферическую

функцию Р„ (соз ф), входящую в выражение (111.21), представить как функцию

координат 0 и А,

(соз ф) = Р

(соз 0) Р

(соз 0') + 2

(га

— к)

(п+к) !

[соз кХ соз кХ' + 31 п &Азт

кХ"]

к=1

хР„Д0) РпЛП

(III.26)

Доказательства этого соотношения мы не приводим. Формула (111.26)

показывает, что сферическая функция степени п может быть представлена

в виде линейной комбинации основных функций

Функции вида

Рп (СОЗ 0), Рпк Ф) СОЗ кх и! Р

пк

(0) 81П кХ.

пк

(В)созкХ и Р

пк

ф)ёткХ

называются присоединенными сферическими функциями. Функция Р

пк

(0) назы-

вается присоединенной функцией Лежандра и вычисляется по формуле

Рпк

(9) =

8111*

п (С

^ .

(йсозб )

(Ш.27)

При к = 0 присоединенная функция превращается в полином Лежандра

по

(0) = Р„(созО), (111.28)

который называют главной сферической функцией.

Главная сферическая функция является функцией лишь одной перемен-

ной — полярного расстояния 0 (или широты <р). Поскольку 0 = 90 —- ф, то

(соз 0) = Р

(81П

ф).

Присоединенные сферические функции есть функции двух переменных:

0 (или ф) и X. Таким образом, на основании (111.26) можно сделать вывод, что

сферическая функция степени п содержит одну главную сферическую функ-

цию — полином Лежандра Р

(соз 0) и 2п присоединенных сферических функ-

ций. Подставляя (111.26) в (111.21), найдем явное выражение для произвольной

сферической функции У

(0, X), как функции координат 0 и А

где

Упф, а,) = 2 {А

пк

со8кХ + В

пк

8ткХ)Рпк(Щ,

В,

к=о

А„

2ге +

4я

Д/(0', А') Р

(соз0')Ло

= 0

пк '-

2ге+1

(п — к) !

2я (га + А)!

X") соз кХ'Рпкф') (1а

пк

2п+1 (га — к) !

2я {п + к)

{-^/(0', Х')зткХ'Р

кФ')с1а

(111.29)

(III. 30)

Подставив (111.29) в (111.25), найдем разложение заданной на поверхности

сферы функции в бесконечный ряд сферических функций

1,0

0,5

/(0, Я) = 2 2 (А

пк

совкХ + В

пк

зткХ)Р

пк

ф).

п=о к-О

§ 16. КЛАССИФИКАЦИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ

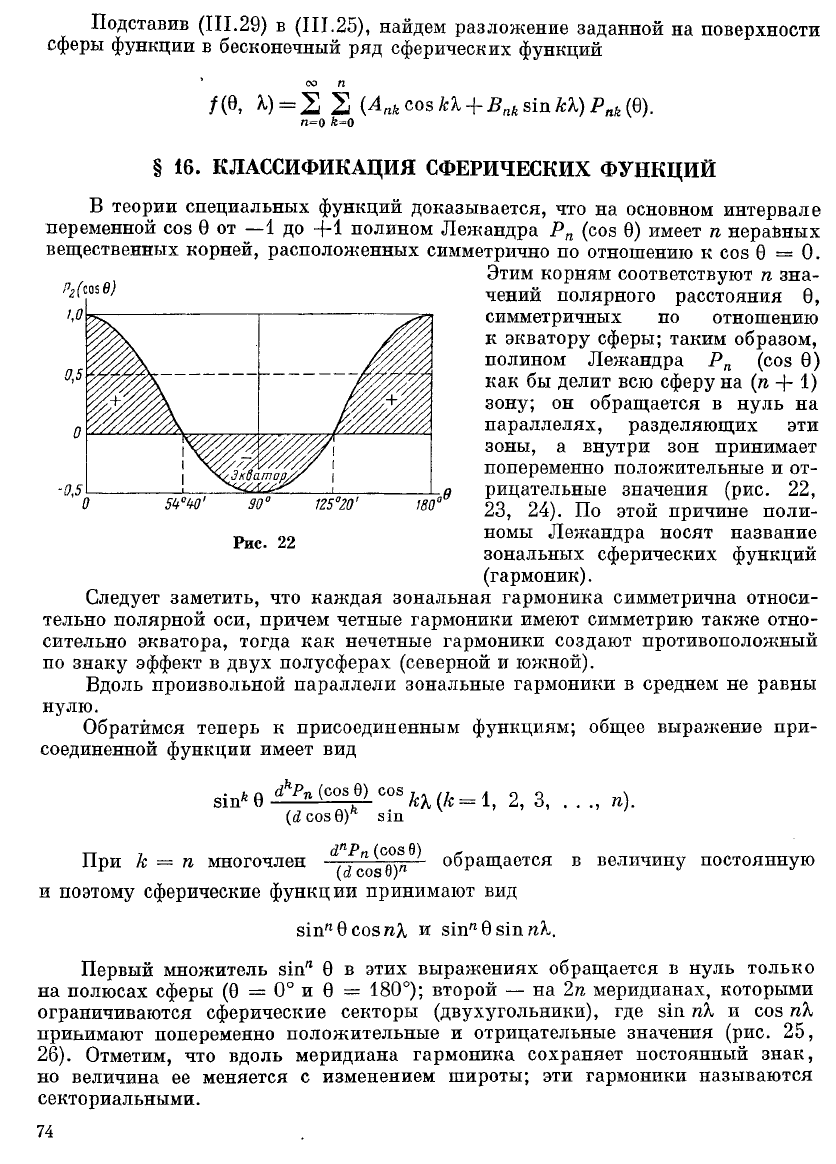
В теории специальных функций доказывается, что на основном интервале

переменной соз 0 от —1 до +1 полином Лежандра Р

(соз 0) имеет п неравных

вещественных корней, расположенных симметрично по отношению к соз 0 = 0.

Этим корням соответствуют п зна-

г(

жв

) чений полярного расстояния 0,

симметричных по отношению

к экватору сферы; таким образом,

полином Лежандра Р

(соз 0)

как бы делит всю сферу на (п + 1)

зону; он обращается в нуль на

параллелях, разделяющих эти

зоны, а внутри зон принимает

попеременно положительные и от-

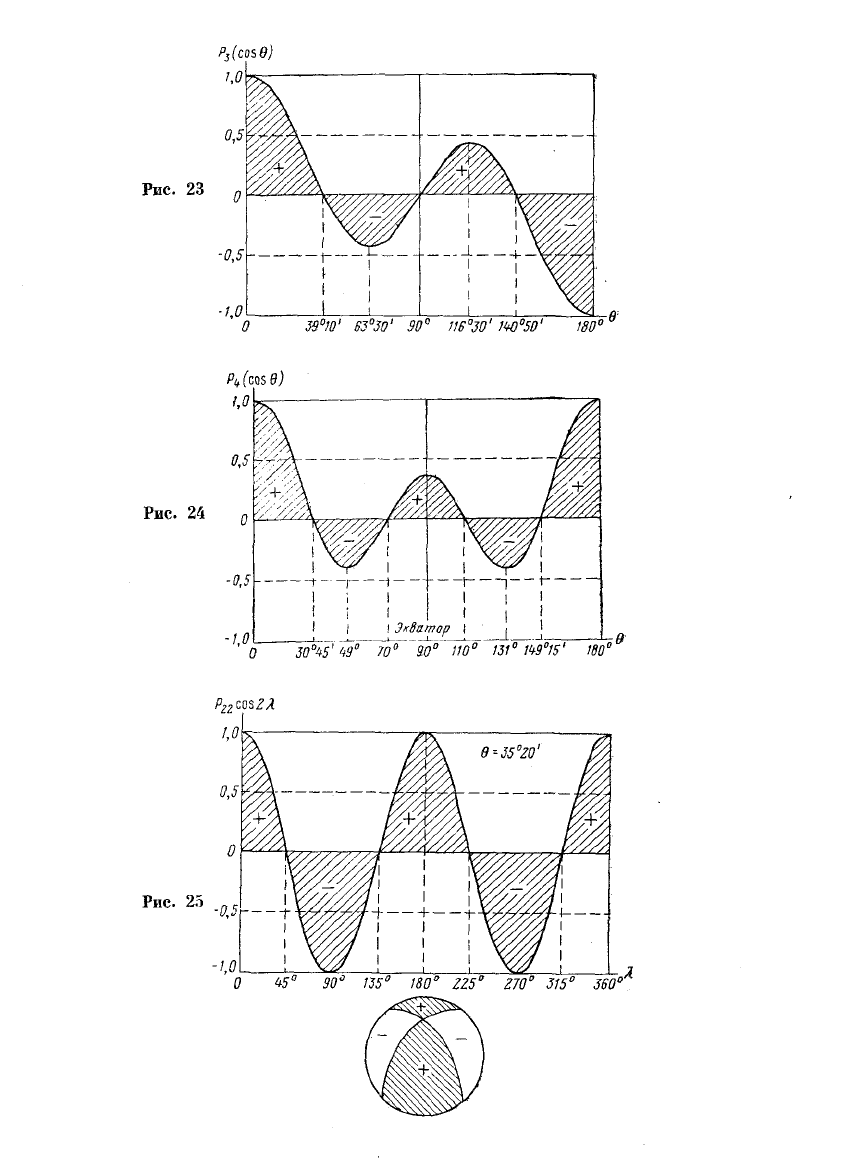
рицательные значения (рис. 22,

23, 24). По этой причине поли-

номы Лежандра носят название

зональных сферических функций

(гармоник).

Следует заметить, что каждая зональная гармоника симметрична относи-

тельно полярной оси, причем четные гармоники имеют симметрию также отно-

сительно экватора, тогда как нечетные гармоники создают противоположный

по знаку эффект в двух полусферах (северной и южной).

Вдоль произвольной параллели зональные гармоники в среднем не равны

нулю.

Обратимся теперь к присоединенным функциям; общее выражение при-

соединенной функции имеет вид

Рп (соз 6) соз

(Д

1 2, 3, ..., п).

(й соз 0) зт

-0,5

•Г"

ш/\

торА/ |

90°

Рис. 22

125''го'

(соз 9)

(ЙСО8 0)

и поэтому сферические функции принимают вид

При к — п многочлен

обращается в величину постоянную

зт"©созпХ и 8т"0зтгаА,.

Первый множитель зт" 0 в этих выражениях обращается в нуль только

на полюсах сферы (0 = 0° и 0 = 180°); второй — на 2п меридианах, которыми

ограничиваются сферические секторы (двухугольники), где зт пХ и соз пХ

принимают попеременно положительные и отрицательные значения (рис. 25,

26). Отметим, что вдоль меридиана гармоника сохраняет постоянный знак,

но величина ее меняется с изменением широты; эти гармоники называются

секториальными.

Ри(СОЗ 0)

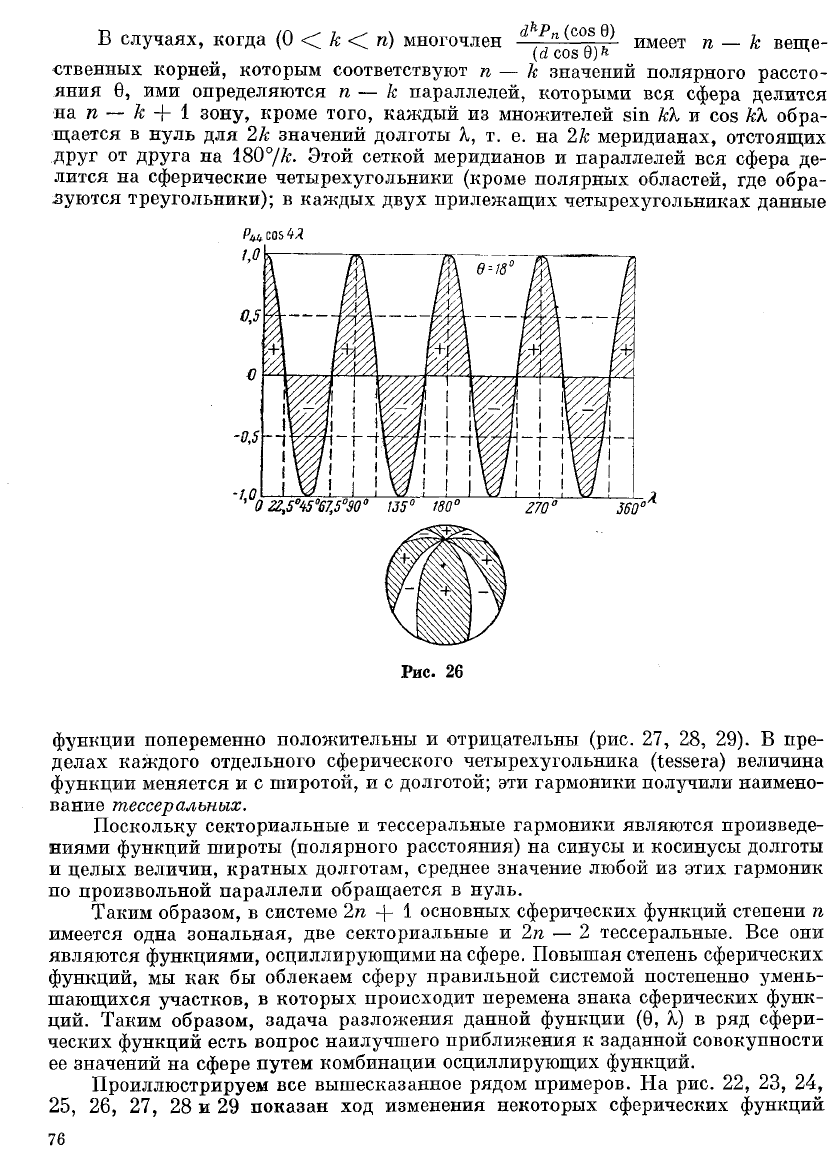
В случаях, когда (0 < к < га) многочлен

(с0

,^ имеет п — к веще-

ственных корней, которым соответствуют п — к значений полярного рассто-

яния 0, ими определяются га — к параллелей, которыми вся сфера делится

на га — к + 1 зону, кроме того, каждый из множителей вш кХ и соз кХ обра-

щается в нуль для 2к значений долготы X, т. е. на 2к меридианах, отстоящих

друг от друга на 180°/к. Этой сеткой меридианов и параллелей вся сфера де-

лится на сферические четырехугольники (кроме полярных областей, где обра-

зуются треугольники); в каждых двух прилежащих четырехугольниках данные

Р/,4 005 М

функции попеременно положительны и отрицательны (рис. 27, 28, 29). В пре-

делах каждого отдельного сферического четырехугольника (1еззега) величина

функции меняется и с широтой, и с долготой; эти гармоники получили наимено-

вание тессералъных.

Поскольку секториальные и тессеральные гармоники являются произведе-

ниями функций широты (полярного расстояния) на синусы и косинусы долготы

и целых величин, кратных долготам, среднее значение любой из этих гармоник

по произвольной параллели обращается в нуль.

Таким образом, в системе 2га + 1 основных сферических функций степени га

имеется одна зональная, две секториальные и 2га — 2 тессеральные. Все они

являются функциями, осциллирующими на сфере. Повышая степень сферических

функций, мы как бы облекаем сферу правильной системой постепенно умень-

шающихся участков, в которых происходит перемена знака сферических функ-

ций. Таким образом, задача разложения данной функции (0, X) в ряд сфери-

ческих функций есть вопрос наилучшего приближения к заданной совокупности

ее значений на сфере путем комбинации осциллирующих функций.

Проиллюстрируем все вышесказанное рядом примеров. На рис. 22, 23, 24,

25, 26, 27, 28 и 29 показан ход изменения некоторых сферических функций

Рис. 28 -5"

115"

и области, на которые делится ими сфера, с указанием того знака, который эти

функции принимают в пределах каждой области. Так, например, на рис. 22

мы видим, что зональная гармоника второй степени — Р

(соз 0) на северном

и южном полюсах принимает максимальные значения [Р

(сов 0) = +1],

а на экваторе имеет минимум [Р

(соз 0) = —

]. Всю поверхность сферы

эта гармоника делит на три области: первая область — от северного полюса

до широты ф^- = 35° 20', в которой функция положительная, вторая область —

от широты ф

= 35° 20' до широты ф

= 35° 20', где гармоника отрицательна,

и третья область — от широты ф

= 35° 20' до южного полюса, в которой

гармоника вновь имеет положительные значения.

Следует обратить внимание, что третья зональная гармоника (см. рис. 23),

как и любая зональная гармоника нечетной степени, производит противополож-

ный эффект в северном и южном полушариях сферы, тогда как зональные гар-

моники четной степени (см. рис. 22 и 24) симметричны относительно экватора.

Секториальные гармоники Р

соз 2Х (см. рис. 25) и Р

соз 4Х (см. рис. 26)

делят всю поверхность сферы на сферические секторы, в которых знаки по-

очередно меняются, первая функция делит сферу на четыре сектора, а вторая —

на восемь.

Наконец, тессеральная гармоника Р

соз X (см. рис. 27) делит сферу на

два сектора и четыре зоны, функция Р

соз 2Х на четыре сектора и три зоны

(см. рис. 28) и, наконец, функция Р

соз ЗА — на шесть секторов и две зоны

(см. рис. 29).

Приведем несколько примеров на вычисление сферических функций.

Прежде всего, имея значения полиномов Лежандра первой и второй степени,

вычислим полиномы Лежандра третьей и четвертой степени. Для этого вос-

пользуемся рекуррентной формулой (111.10).

Полагая п = 2, получим

(СОЗ

0) =

СОЗ

вР

(СОЗ

0)— уРх (соз 0) =

соз 0 (-| соз

0 - -

— соз 0 = у соз

0 — соз 6,

при п — 3 будем иметь

(соз 0) = ^ соз 0Р

(соз 0) -

(соз 0) = 1 соз 0 (у соз

0 — соз в) —

-т(Т

соз20

-У)=-Х

соз40

-Х

820

+4-

Продолжая этот процесс далее, можно получить полином Лежандра любой

степени п.

Для образования системы присоединенных функций вычисляют присоеди-

ненные функции Лежандра в следующем порядке:

от многочлена Лежандра берут ряд последовательных производных по

аргументу соз 0;

Таблица 1

п0

пк

пп

0 1

СОЗ 0 —

3111

С032 0

3 81П0СО8 0 3 ЗЩ2 0

-Ц- С08

0 — СОЗ 0

-|-81П0(5СО82 0 —1)

15 81П

2 15 зт2 0 С08 0

—- СОЗ

Э_^СО320+А

-|-ЗШ0(7 СОЗ® 0—3 соз 9)

4^-81112 0 (7С032 9 — 1)

105 зш

0 соз 0

105 81114 0

^ ^СО8

0 —

а ,

гЛ

— СО8

0 + "2^- СОЗ 0 )

УЯПЕ ^СОЗ4 0-|--СО32 0+^-)

31П2 0 ^ СОЗ

•

СОЗ 0 ^

В1П

ЗЕ ^00820—1.)

945

81Ц4

0 соз 0

945 зт5 0