Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Подставляя значения

= Х — х

; а

= У—у

; а

= 2—2

_ д\У

_ дШ _ _т_

ёх—

дх

; 8у—

ду

; ёг

получим уравнение касательной плоскости

Так как первые производные потенциала всюду непрерывны, то и наклон

этих плоскостей меняется непрерывно.

Уравнение уровенных поверхностей потенциала силы тяжести имеет вид

ТУ (х, у, Г) = СОПБ1.

Давая различные значения постоянной, будем получать различные уровен-

ные поверхности. Уровенная поверхность потенциала силы тяжести, совпада-

ющая в открытом океане с невозмущенной поверхностью воды, называется

геоидом.

Ввиду однозначности потенциала уровенные поверхности не могут пере-

секаться. Расстояние между двумя бесконечно близкими поверхностями, как

видно из (IV.9), обратно пропорционально величине силы. Но сила тяжести

на уровенной поверхности не является постоянной ни по величине, ни по на-

правлению, а поэтому расстояние между двумя уровенными поверхностями

в различных местах различно. Известно, что сила тяжести на полюсах больше,

чем на экваторе, и, следовательно, на полюсах уровенные поверхности рас-

полагаются ближе друг к другу, чем на экваторе.

Из непрерывности потенциала силы тяжести вытекает, что все уровенные

поверхности непрерывны и, как мы уже видели, наклон касательной плоскости

также меняется непрерывно. Однако кривизна уровенной поверхности опре-

деляется вторыми производными потенциала и потому кривизна уровенных

поверхностей (в том числе и геоида), пересекающих слои различной плотности,

изменяется скачком там, где меняется скачком плотность.

Определим кривизну нормального сечения уровенной поверхности. Если

уравнение поверхности задано в форме

2=1{х, у),

то кривизна нормального сечения, образующего угол А с осью х, определяется

формулой

4 = гсо8

Л + $8т2Л + г8т

.4, (IV. 14)

где р — радиус кривизны нормального сечения, а

~~дхЪ'

~ дх ду '

~~ду*'

согласно обозначений Монжа.

Уравнение уровенной поверхности имеет вид И

(х, у, г) = сопз1, где ТУ —

функция координат х, у, г, не разрешенная относительно г. Образовав вторые

100

производные от И

, считая, что г является неявной функцией переменных х

и у и направлена по вертикали вниз, получим

_ 1 дт 1 ЗУ _ 1 дт

~ 8 дх* ' е дхду'

~ в ду* •

Подставив эти значения в (IV. 14), получим формулу для определения

кривизны уровенной поверхности

д2

М' * 2

, •

О Л

I • 2

/ПТЧСЧ

-~д±г

008

8Ш А

1у

Кривизна геоида, как и всякой уровенной поверхности, в местах, где он

зересекает материковые массы, изменяется скачком и поэтому всякое продол-

жение аналитическими методами поверхности геоида внутрь притягивающих

«асс не будет соответствовать действительному положению геоида. Потенциал

•гвлы тяжести вне масс и внутри масс выражается разными аналитическими

функциями, а потому и уравнение геоида не может быть выражено одной ана-

литической функцией

Выясним физический смысл вторых производных потенциала IV. Возьмем

Ъвчало прямоугольных координат в точке М земной поверхности. Направим

*ь гпо отвесной линии внутрь Земли, а оси хм у — на север и на восток соот-

ветственно.

В таком случае

_ т

дг '

Представим вторую производную как

дт д / дш

_ де

дт.

V дг )

~~ дт,

показывает, как изменяется сила тяжести в направлении вертикали и по-

тому называется вертикальным градиентом силы тяжести.

Представив аналогичным образом производные

дт ^ д /

д1У \

_ дв

дхдя дх \ дг ) дх '

^ _

(

\ ^

ду да

—

ду \ ) ~ ду '

7^еждаемся, что они характеризуют изменение силы тяжести в горизонтальной

носкости: первая в направлении меридиана, а вторая в направлении первого

вертикала; эти производные называются горизонтальными градиентами силы

тяжести.

Полным горизонтальным градиентом называется геометрическая сумма

лекторов д$/дх и д$/ду, т. е. вектор д§/дв, указывающий направление, в кото-

ром сила тяжести возрастает (или убывает) быстрее всего. Величина его равна

—

1/7ЖУТ7ЖТ

_ т/(у

(^ у

дз V \ дх ) \ ду ) г

дх дг ) "г ^

ду дг

) '

101'

а угол с осью х, т. е. азимут, определяется формулой

де дт

ду дх дг

дё дт

дх ду дг

Вторые производные д

]Ф/дх, д

\У/дхду, д

\У/ду

, как мы видели (IV. 15).

характеризуют кривизну нормального сечения уровенной поверхности.

Если в (IV. 15) положить А = 0, получим кривизну меридионального

8 л /о

сечения = —если А =

л/2,

— кривизну сечения уровенной по-

верхности плоскостью первого вертикала

дт _

~ Р у '

Выведем формулу для вертикального градиента силы тяжести. Для этого

напишем выражение (1У.6) в развернутом виде

дт , дт , дт ... .

0 2

/пт-^

и, подставив в него значения производных д

\У/дх

и д

Ш/ду

, получим

— формула показывает зависимость вертикального градиента силы тяжести от

плотности. Из нее следует, что редуцирование силы тяжести внутри притягива-

ющих масс точно выполнить невозможно без детального знания закона распре-

деления плотностей.

Напротив, во внешнем пространстве, где притягивающие массы отсут-

ствуют, редуцирование силы тяжести может быть выполнено без привлечения

данных о строении земной коры. Формулой (1У.17) удобно пользоваться в слу-

чае, если кривизны нормальных сечений уровенных поверхностей в перпен-

дикулярных направлениях известны,

§ 21. РАЗЛОЖЕНИЕ ПОТЕНЦИАЛА СИЛЫ ТЯГОТЕНИЯ

В РЯД ПО ШАРОВЫМ ФУНКЦИЯМ.

ПРИБЛИЖЕННОЕ ЗНАЧЕНИЕ ПОТЕНЦИАЛА ЗЕМЛИ

Если представить потенциал силы тяготения в виде бесконечного ряда,

то задача определения потенциала сводится к последовательному суммирова-

нию отдельных членов этого ряда. Ограничиваясь заданным членом разложе-

ния, мы, естественно, получим приближенное значение потенциала, но степень

приближения при этом в принципе может быть безграничной, если брать не-

ограниченно большое число членов. Число членов разложения определяется

требованиями необходимой точности вычислений, а также наличием необхо-

димого материала, полученного из наблюдений.

Итак, рассмотрим вопрос о разложении потенциала силы тяготения в ряд

по шаровым функциям. Пусть дано некоторое тело с массой М.

102'

Потенциал силы тяготения тела в любой точке, определяемой сфериче-

скими координатами р, 0, X, имеет вид (1.20)

У(р, 0, (IV. 18)

Если через р', 0', X' обозначить сферические координаты текущей точки,

по которым ведется интегрирование, то элемент объема можно представить

в виде

Определим потенциал тяготения вне сферы, окружающей тело (рис. 31).

Поскольку р ]> р', функция — может быть представлена сходящимся рядом

(111.18), в котором В заменен на р'

1 о

/п

"7= (С081|;),

(1У.19)

п=0

Р(Р,9,Л)

Рис. 31

а соз

я|>

определяется формулой (111.17). Подставим в (ГУ.18) вместо у ряд

(1У.19) и после почленного интегрирования получим

со

у (р. 0. я) = / 2 фг ЭД ( 6р

,пр

п (сов ф) йх. (IV.20}

71=0

Введем далее обозначение

(0, X) =

Щ бр

,п

(соз

я|>)

(1У.21)

=одставив сюда значение Р

(соз

<ф)

из (III.26), получим функцию 2

(0, X)

в явном виде

(9, X) = Р

(соз в) / Щ бр'

(соз 0') ах +

+ 2

2 [

со8

кк

•* Щ

ви со8

(

к=1 и т

+ 8Ш кх

•

/ Ц^ бр'

31П

кХ'Рпк (В') ах| Р

пк

(0).

103

Объемные интегралы, являющиеся коэффициентами полученного 7ряда,

представляют собой стоксовы постоянные (§ 10), поскольку произведение

,п

(соз 0'), р'* соз кХ'Р

пк

(0') и р

/>г

зт к%'Р

пк

(0') являются гармониче-

скими функциями во всем объеме т.

Обозначим эти постоянные

по

=/Щар'

Л,(сове)йт

= 2 / И'

6р'

соз кХ'Р

пЬ

(0') йх

(п +

к)!

"к = 2 / Щ бр'" зт кХ'Р

пЬ

(0')

йх

(1У.22

тогда представим сферическую функцию степени п в виде

(в, I) = Д

л0

(соз 0) + 2 соз

ЛЯ,

+ Е

пк

зт

&Я)

(в). (1У.23'

к-1

Таким образом, внешний потенциал силы тяготения может быть представ-

лен в виде бесконечного ряда шаровых функций

V (Р, 0, Я) = 2 Т^Г 2

(

пк 008 к% + Епк 81п кХ) р,гк (0)

71=0 1_ь=о

(IV.24'

Рассмотрим сферические функции первых степеней. Положив в (ГУ.23.

п = 0, получим сферическую функцию нулевой степени

(0, Я) = п

= / бР

(соз

VI)) Ах

= № (1У.25;

которая является величиной, пропорциональной массе тела.

При п — 1 получим сферическую функцию первой степени

(0>

Я)

СОЗ 0

+ О

СОЗ Я 31П 0

+ Е

81П Я

31П 0,

где

1о

= /Щбр'СО8 0'ЙТ

= / Щ бр' соз я' зт 0' йх

бр'

31П

я' зт 0' йх.

Введем прямоугольные координаты, используя формулы связи между

системами координат (III.2)

Р'СО8 0' = ^

р' соз

Я'

зт

= I

р"

31П я® ЗШ 0*

= Г),

104'

получим

Поскольку координаты центра массы тела вычисляются по формулам

III ^

XXX

° м '

Уо

~ м

; 2

° ~ м '

можно выразить постоянные /)

, Б

и Е

г1

через эти координаты

/М2

/Мж

= /Му

Следовательно, сферическую функцию первой степени можно представить

в виде

(е, Я) = /М[2

соз6 + ;

Го

со8А,з1п0 + у

8тЯзт0]. (1У.26)

Сферическая функция второй степени содержит пять постоянных:

(9,

= /)

(Л (соз 0) + (/>

2Х

соз х +

#21

ап X) Р

(0)

+ (Д

соз 2Х + Е

зт 2х) Р

(0).

Используя значения сферических функций второй степени, приведенные

в табл. 1, представим стоксовы постоянные

=4"

бр

23 008 6

81п 008

•-

бр"

ЗсО3 0'

8111

0' ЗШЯ'ЙТ

= ±. ^

бр'

3 зт

0' соз IX' йх

= ^ 0 $ бр"

81П

2х' йх

В прямоугольной системе координат

4 Р'

соз

0' —^ = {(2^

Ъ*

- ц*) =

=| (V +

+ ^ - -

2г

(IV. 27)

105

поэтому постоянную Л

можно представить в таком виде

Ого

= У

<Ч"

С") •Лх

+ { Щ б (I

Ах

-/ Щ б (Р + п

) йт.

Т X х

Это позволяет выразить постоянную /)

через моменты инерции тела

относительно координатных осей х, у, г, которые вычисляют по формулам

А = Щб(т|» + &

)Л

X '

с = щ 6(|

+г1

)йт.

Получим

#20(IV. 28)

Выразим в прямоугольной системе координат и другие постоянные

= Е

= 1^ЬЪцАх, Я

= /Щб|г]йт. (1У.29)

XXX

Интегралы, стоящие в правых частях полученных равенств, представляют

собой произведения инерции и определяют направление главных осей инерцип

тела. Они обращаются в нуль, если оси координат совместить с главными

осями инерции.

Представим постоянную /)

следующим образом:

=1Щ бр"

8Ш

0' (СОЗ

Г -

81П

Г) Ах =

[

2 81п2

0083

2 81п2 9

з1п2

йт

переходя к прямоугольным координатам, получим

Огг = Т И!

6 (5>

~ ^

{В

Л)

(1У

30)

Таким образом, все стоксовы постоянные второго порядка имеют простой

механический смысл: они определяют разности моментов инерции и произведе-

ния инерции данного тела.

Каждый член разложения потенциала в той или иной степени характери-

зует фигуру уровенной поверхности данного тела. Так, если бы тело имело

строго сферическую форму, то в разложении (1У.24) был бы один единственный

член нулевого порядка и потенциал имел бы вид

^(р, е, •

106'

Все последующие члены разложения учитывают уклонение формы притя-

гивающего тела от сферической.

Постоянная 0

2(>

обусловлена сжатием тела около полярной оси (для шара,

очевидно, А = В = С и />

обращается в нуль, чем сильнее вытянуто тело

вдоль экватора, тем больше будет отличие экваториальных моментов инерции

от полярного) и член разложения (соз 0), изменяющийся только в зави-

симости от широты, характеризует степень полярного сжатия.

Остальные четыре функции второй степени, зависящие от долготы, характе-

ризуют вариации потенциала по долготе, и в случае, если тело по своей форме

близко к телу вращения (как, например, Земля), то влияние их весьма мало.

Отметим, что одна из них, а именно член с /)

, характеризует экваториальное

сжатие тела, поскольку значение постоянной /)

зависит от разности эквато-

риальных моментов инерции.

Окончательно потенциал тяготения во внешнем пространстве может быть

представлен рядом

У(р, 0, = + (2

соз0 + х

созХ8т0 + у

8тЯ,зт

Р Р

+-рг [/

(^Ч^- -

)

сов2 0

т)+

со81

в1п

0 со5 9

+ 3 |я

зт

2Л

+ / соз 2я) зт

0] + 2 • (1У.31)

п-3

ЭТО разложение справедливо при любом произвольном выборе начала

и осей координат. Если начало координат считать совмещенным с центром

массы тела, а координатные оси — с главными осями инерции, то ряд (1У.31)

будет иметь более простой вид

г,* е,

Х[(^-с)(1соз'9-±)

ОО

+1 (В - А) соз 2А зш

0] + 2 ^фА. (1У.32)

п-З

Чаще разложению потенциала в ряд по сферическим функциям придают

иной вид.

Заметим, что коэффициенты при сферических функциях в разложениях

(1У.31) и (IV.32) имеют различную размерность. Так, если у постоянной И

размерность Щ, то у членов Б

, Е

гг

размерность /М X см, члены вто-

рого порядка имеют размерность Щ X см

и т. д. Удобнее иметь при сфери-

ческих функциях безразмерные коэффициенты. Для этого вынесем в разложе-

нии (IV.24) за скобки общий множитель Тогда получим

У<р. е. = ^

со п 1

2 2 7м^

{

пк со8 кх+Епк 81п кК) Рпк (0);

п=1 к=0 ^

107'

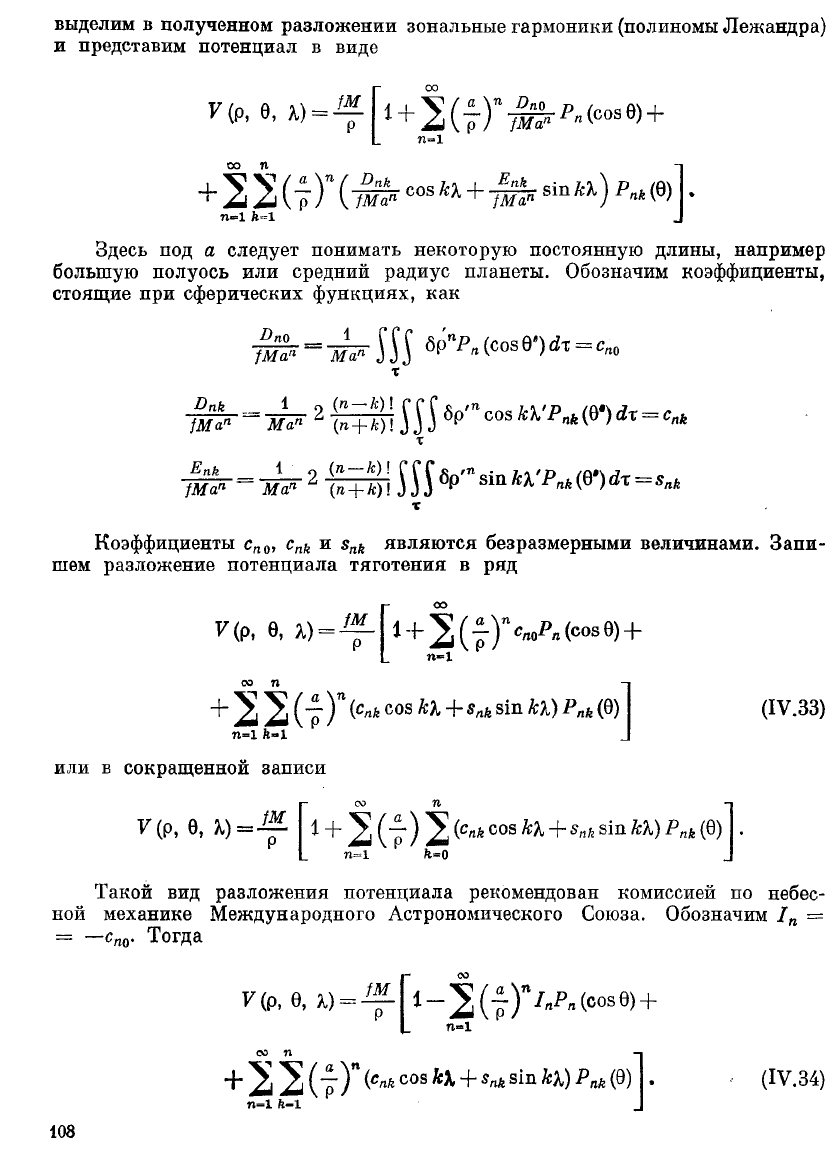
выделим в полученном разложении зональные гармоники (полиномы Лежандра)

и представим потенциал в виде

г<р, в,

п-1

^ 2 2 Ш/^

003

^ +

з1п кК

)

* ®

п=1 к=1

Здесь под а следует понимать некоторую постоянную длины, например

большую полуось или средний радиус планеты. Обозначим коэффициенты,

стоящие при сферических функциях, как

Рпо

/Ма

Ма

Щ бр

Р„(СО8 0')ЙТ =

Опк

/Ма

Ма

ётШ Ш

вр,в со3

кХ

Рпк

(0,) ах=

Епк

{Ма

Ма

(га + А)

Коэффициенты с„

, с„& и $

л6

являются безразмерными величинами. Запи-

шем разложение потенциала тяготения в ряд

У(р, е, х)=^[1 + 2(7)"

*о

С03

СО П -1

+ 22(7)" (

Спк 008 кК+$пк 31п Рпк

п=1 й-1

(1У.ЗЗ)

или в сокращенной записи

, 0,

со /с

1 + 2(7)2 (°

пк 003 +8пк 31п Рпк

п=1 к=о

Такой вид разложения потенциала рекомендован комиссией по небес-

ной механике Международного Астрономического Союза. Обозначим 1

= — с

п0

. Тогда

п-1

(005 0) +

оо п -|

+ 22(7)

003 + 31П

?Пк (9)

(1У,34)

п=1 й-1

108'

Если планета по своей форме является телом вращения, тогда в разложе-

нии потенциала останутся только зональные гармоники

Используя полученное разложение потенциала тяготения для любого тела

в ряд шаровых функций, определим приближенное значение потенциала Земли.

Пусть под телом с массой М понимается Земля. Тогда, сохраняя в (IV.32)

полином Лежандра второй степени, получим формулу для вычисления прибли-

женного потенциала силы тяготения Земли

г<р, е,

где А

= средний экваториальный момент инерции Земли.

Поскольку на основании (III.2)

+ у

р2

81п

2е

потенциал центробежной силы можно представить в виде

Приближенный потенциал IV' силы тяжести получается как сумма потен-

циалов V' и ^

РГ(Р, е, X) = Щ- +

/ (Л

(-|

соз

-1) + р

зш

8. (1У.35)

§ 22. ПРОБЛЕМА ОПРЕДЕЛЕНИЯ ВНЕШНЕГО

ГРАВИТАЦИОННОГО ПОЛЯ И ФИГУРЫ ЗЕМЛИ

При изучении фигуры Земли (и других планет) приходится иметь дело

исключительно с внешним потенциалом.

Первым ученым, которому удалось доказать принципиальную возмож-

ность определения внешнего потенциала независимо от плотности, был Стоке

(1849 г.).

В основе теоретических исследований Стокса лежит его знаменитая тео-

рема, которая может быть сформулирована следующим образом: если известны

и форма внешней уровенной поверхности а целиком охватывающей все притя-

гивающие массы, то потенциал силы тяжести IV и сама сила тяжести § опре-

деляются однозначно как во всем внешнем пространстве, так и на самой уровен-

ной поверхности а. Очевидно, теорема Стокса будет доказана, если показать,

что потенциал силы тяжести не изменится при перераспределении масс внутри

поверхности а, при условии, что сама поверхность о продолжает оставаться

внешней уровенной поверхностью и при новом распределении масс.

Предположим, что имеется два распределения масс: первому соответствует

потенциал притяжения V', а второму V". Потенциал центробежной силы, как

независящий от притягивающих масс, будет в обоих случаях один и тот же.

109'