Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Эта величина крайне мала. При А а — 100 м она составляет 1,5 X 10~

чему соответствует изменение знаменателя сжатия на 0,014 единицы.

Из теоремы Клеро

I а 5 17

а + М-у?—д-? а

следует, что нормальные формулы, соответствующие этим эллипсоидам, будут

содержать один и тот же коэффициент (3, а различием в коэффициентах (5,

можно пренебречь (изменение у

, обусловленное изменением р

никогда не

превосходит 0,001 мгл).

Если при принятой точности задачи можно пренебречь такими измене-

ниями "у

(а следовательно, и аномалий силы тяжести), то можно считать, что

полуось уровенного эллипсоида такова, что потенциал на его поверхности

равен потенциалу Земли на уровне моря. Полуось такого эллипсоида а + Да

остается неизвестной. Ее можно определить, например, из градусных измере-

ний. Как только она будет известна, параметр Ш

можно вычислить.

Глава VI

ВОЗМУЩАЮЩИЙ ПОТЕНЦИАЛ

§ 29. СВОЙСТВА ВОЗМУЩАЮЩЕГО ПОТЕНЦИАЛА

Возмущающим потенциалом Т Земли принято называть разность между

действительным И

и нормальным II потенциалами Земли

—

]У

—

II. (VI. 1)

Представим потенциал силы тяжести Земли IV как сумму потенциала II

силы притяжения и потенциала центробежной силы

= 7 +

Аналогично нормальный потенциал может быть представлен в виде

где II

— потенциал притяжения уровенного эллипсоида, & — потенциал

его центробежной силы.

Поскольку выше было установлено, что различием центробежных потен-

циалов Земли и уровенного эллипсоида можно пренебречь, найдем, что Т пред-

ставляет разность потенциалов тяготения Земли и уровенного эллипсоида

Т = У—Ущ. (У1.2)

Возмущающий потенциал Т обладает всеми свойствами потенциалов тяго-

тения; его первые производные непрерывны во всем пространстве, во всем

внешнем пространстве возмущающий потенциал удовлетворяет уравнению Лап-

ласа

ДГ = 0,

и на бесконечности является функцией регулярной.

Эти свойства возмущающего потенциала Земли позволяют для его опре-

деления во внешнем пространстве использовать метод краевых задач с тем

или иным краевым условием, заданным на земной поверхности. Однако необхо-

димо отметить одно принципиальное затруднение, возникающее при решении,

этой задачи, а именно, поверхность, на которой задается граничное условие,

должна быть известной. В нашем случае граничное условие удовлетворяется

на поверхности Земли, которая сама подлежит определению. Поэтому прихо-

дится граничное условие, которому возмущающий потенциал Т удовлетворяет

131

в точках физической поверхности Земли, относить к той или иной известной

поверхности и задачу решать методом приближений.

Получим разложение возмущающего потенциала Т в ряд по шаровым

функциям. Для V

согласно (1У.31) получим

(

р, 9, + |

, (У1.3)

п=2

где М

— масса уровенного эллипсоида; Р°

— коэффициенты при полиномах

Лежандра Р

(соз 0).

Ряд (VI.3) не содержит присоединенных сферических функций потому,

что эллипсоид является телом вращения и его потенциал не зависит от долготы.

Поскольку центр масс эллипсоида совмещен с его геометрическим центром,

в разложении (VI.3) будет также отсутствовать сферическая функция первой

степени.

Согласно (VI.2), вычитая почленно (VI.3) из (IV.31), получим для возму-

щающего потенциала

Т(Р, 8,

^_[

2оС08

(

а:оС

о5Х + у

зшЯ)8ш9] +

, у 2„(8, Ь)-ПРп(соз 9) ГпФ, Я)

П=2 ^ 71=0

Если же потенциал тяготения Земли представить в форме (1У.ЗЗ), то разло-

жение потенциала V

будет

у°{р, е, 1)=^[1+ё

(-^-)

(созе)-!-7

(-^)

(созе)+...]

и соответственно

оо п

Т{

Р, 6,

я)=

/<*-*.)

Ж ^(А^со,их + 5ШЩР

пк

(9), (У1.4*)

п=1 к=О

где с

п0

= с

п0

—с

п0

, с

пк

= с

пк

и во всех членах кроме первого положено М =

= М

Если нормальный потенциал задан в форме

уэ

Мо. ["

2о

(Ау р

(соз е)

- у р

(С08 е)

] + «р.

в1п

» 9,

(VI.4**)

т. е. потенциал V

представлен с учетом сферической функции нулевого по-

рядка и зональных гармоник второго и четвертого порядка, то уровенная

поверхность нормального потенциала при р = а не будет являться эллипсоидом

вращения. Это будет поверхность, близкая к сфере, которую принято называть

сфероидом. Сфероид может быть определен как простейшая из поверхностей,

отклонение которой от сферы характеризуется зональной гармоникой второго

порядка. В этом случае при вычислении возмущающего потенциала по фор-

муле (У1.4*) следует положить с

= с

—с

, с

= с

—с

, с

п0

= с

п0

(при

п > 4), с

пк

= с

пк

(при любых значениях п).

132

Если бы некоторые стоксовы постоянные Земли были бы достаточно точно

известны, то при выборе нормального потенциала можно было бы поставить

условие, чтобы соответствующие стоксовы постоянные Земли и эллипсоида,

стоящие в качестве коэффициентов при сферических функциях 2%, (0, X) и 7,п (9),

были бы в точности равны. Например, можно было бы поставить условие,

чтобы масса эллипсоида равнялась массе Земли (М

= М), чтобы центр эллип-

соида совпадал с центром масс Земли (х

= у

= г

= 0) и т. д. Тогда в раз-

ложении (VI.4) соответствующие сферические функции отсутствовали бы.

В общем случае возмущающий потенциал содержит сферические функции

всех степеней.

§ 30. СВЯЗЬ МЕЖДУ ВОЗМУЩАЮЩИМ ПОТЕНЦИАЛОМ

И СОСТАВЛЯЮЩИМИ УКЛОНЕНИЯ ОТВЕСА

Вследствие отличия действительного гравитационного поля Земли от

нормального, обусловленного сложностью ее внутреннего строения и фигуры,

направление вектора действитель-

ной силы тяжести § (отвесной

линии) в точках физической по-

верхности Земли не совпадает

с направлением вектора нормаль-

ной силы тяжести у. По этой

причине астрономические коор-

динаты точек земной поверхности

отличаются от геодезических.

Установим зависимость между

этими координатами.

Проведем в точке М земной

поверхности три направления

векторов; действительной силы

тяжести д, нормальной силы

тяжести у и нормали к эллипсои-

ду п. Пересечение этих напра-

влений с небесной сферой опре-

делит положение астрономического зенита 2

, точки Х

и геодезического

зенита (рис. 34). Отметим на сфере положение полюса Р.

Из рисунка видно:

^ 2

Р = 90 -

;

уу2

Р = 90 — В;

А. 2

Р2

— АХ,

где ф — астрономическая широта точки М\ В — геодезическая широта точки

М: АХ — угол между астрономическим и геодезическим меридианами точки М.

Так как астрономические и геодезические долготы отсчитываются от одного

начального меридиана, то

АХ^Х — Ь.

90-В

133'

Угол (п, у) между направлением нормали к эллипсоиду п и направлением

нормальной силы тяжести у равен разности между нормальной и геодезической

широтой и согласно (У.47)

(п, у) = В

-В= зш2В.

' " " Я 81111

На сфере он измеряется дугой 2

= ДВ.

Угол (у, §) между направлением нормальной силы тяжести у и направле-

нием отвесной линии в точке М {$) называется уклонением отвесной линии.

На сфере он измеряется дугой 2

= и. Для полной характеристики уклоне-

ния отвеса необходимо знать, кроме его абсолютной величины и, азимут плос-

кости, в которой расположен этот угол. Однако удобнее уклонение отвесь

определять его проекциями на плоскости меридиана и первого вертикал г

^ нормального поля. Проведем из точки 2

;

дугу 2

, перпендикулярную к геодезическому

меридиану Р2

. Введем обозначения: ^ 2^2^ = с

(проекция уклонения отвеса на плоскость мерп-

"/Т диана), ^ 2

= т] (проекция уклонения отвеса

на плоскость первого вертикала). Из сфериче-

ского прямоугольного треугольника 2^2

1> по-

лучим

сов (X

- Ь) = 1

с1в (В + АВ +1);

31П

Г]

81П

(X — Ь) С08 ф.

Раскладывая зт (Х—Ь), соз (А.—Ь) и зт г

в ряды и пренебрегая по малости величинами

(Х—ЬУ, г)

и более высокого порядка, получим

= ф —Б —ДБ ,

(VI.5|

Рис. 35

т) =

(А.

— Ь) созф

Определим зависимость между возмущающим потенциалом и составля-

ющими уклонения отвеса. Примем точку М за начало прямоугольной системы

координат, ось г совместим с направлением нормальной силы тяжести у, ось

направим по касательной к меридиану на север, а ось у — на восток (рис. 35).

Спроектируем угол между направлениями § и у на плоскости меридиана и пер-

вого вертикала. В соответствии с формулами (VI.5) установим правило знаков

для составляющих ^ и т]; если астрономический зенит отклоняется от геодези-

ческого на северо-восток, то составляющие уклонения отвеса считаются поло-

жительными, если на юго-запад, то — отрицательными.

На рис. 35 астрономический зенит отклоняется к юго-западу, а потому

6 = --?-; п = (У1-61

62 62

где ввиду малости углов | и г] тангенсы заменены самими углами. Составля-

ющие силы тяжести связаны с потенциалом Ш соотношениями

«.-ТГ-Я-С+П

ду

134'

Поскольку плоскость ху перпендикулярна к направлению нормальной

силы тяжести, проекции нормальной силы тяжести на эти оси будут, очевидно,

равны нулю

дИ

Ух

дх

Вследствие этого

ди

Уу

~ ду

дТ

и формулы (У 1.6) принимают вид

дх

_ дТ

ду

1 дТ

У дх

1 дТ

У ду

(VI.7)

Здесь с пренебрегаемой погрешностью составляющая §

заменена через у.

Считая, что М + Н ^ N + Н К + Я = р, получим дифференциалы дуг

меридиана и параллели

йх~р йВ

йу —

р соз

В йЬ.

Введя эти значения в (VI.7)

1 =

1 дТ

' ур дВ

1 дТ

•ур

соз В дЬ

(У1.8)

получим окончательные формулы, связывающие возмущающий потенциал

Земли и составляющие уклонения отвеса.

§ 31. НОРМАЛЬНЫЕ ВЫСОТЫ, АНОМАЛИИ ВЫСОТ.

СВЯЗЬ МЕЖДУ ВОЗМУЩАЮЩИМ ПОТЕНЦИАЛОМ

И АНОМАЛИЕЙ ВЫСОТЫ

Геодезическая высота точки М земной поверхности может быть определена

через разность нормальных потенциалов 11

—й

(У.43). Однако в результате

измерений определяется разность действительных потенциалов между значе-

нием потенциала силы тяжести в исходном пункте нивелирования Ш

и значе-

нием потенциала силы тяжести в точке М—И

- величина —\Ум 1Ф°Р~

мула (1У.10)].

Если бы гравитационное поле Земли совпадало с нормальным (в этом

случае возмущающий потенциал всюду был бы равен нулю), то для каждой

точки поверхности Земли соблюдалось бы равенство

135'

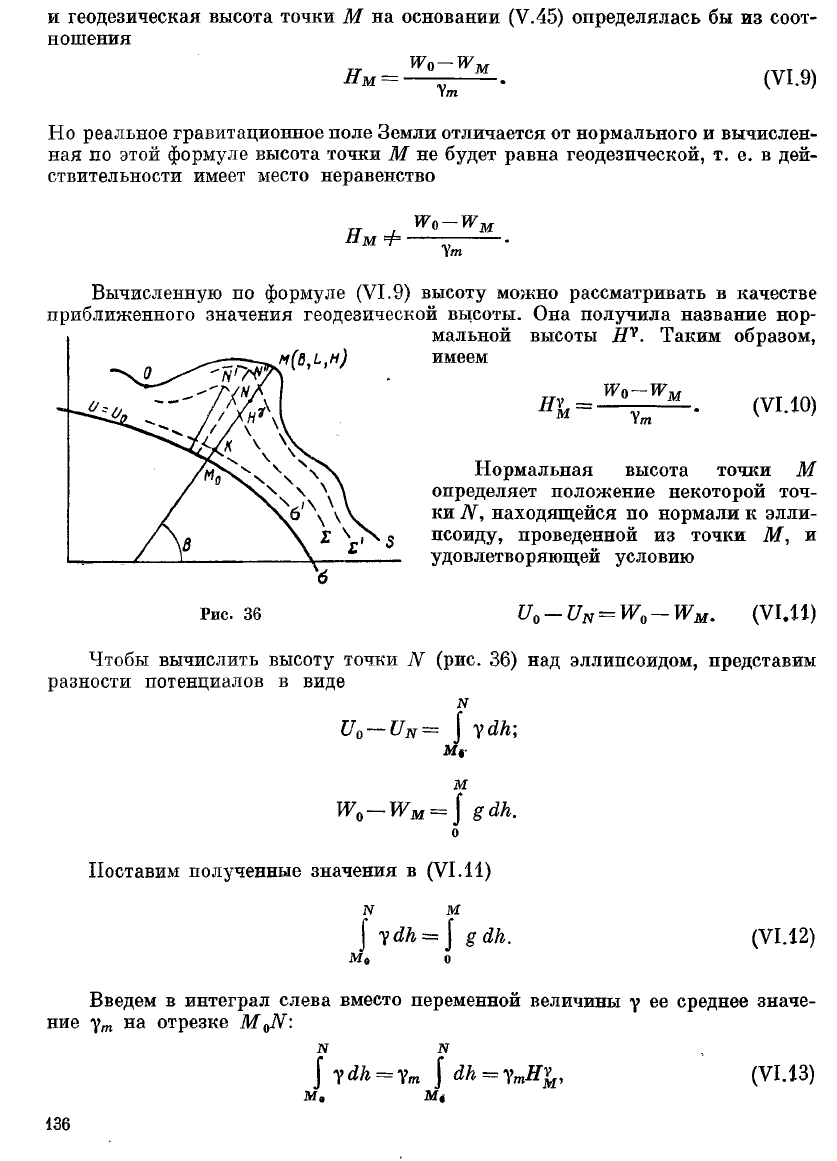
и геодезическая высота точки М на основании (У.45) определялась бы из соот-

ношения

Н-

Ут

(У1.9)

Но реальное гравитационное поле Земли отличается от нормального и вычислен-

ная по этой формуле высота точки М не будет равна геодезической, т. е. в дей-

ствительности имеет место неравенство

Нм Ф

Ут

Вычисленную по формуле (VI.9) высоту можно рассматривать в качестве

приближенного значения геодезической высоты. Она получила название нор-

мальной высоты Н

. Таким образом,

имеем

ну

IV о —№

Ут

(VI. 10)

Нормальная высота точки М

определяет положение некоторой точ-

ки И, находящейся по нормали к элли-

псоиду, проведенной из точки М, и

удовлетворяющей условию

Рис. 36

м-

(VI.!!)

Чтобы вычислить высоту точки N (рис. 36) над эллипсоидом, представим

разности потенциалов в виде

—

ум-,

М,-

Поставим полученные значения в (VI.И)

N М

| уд,к = \ §йк.

Мл о

(VI. 12)

Введем в интеграл слева вместо переменной величины 7 ее среднее значе-

ние у

на отрезке М

N N

йк = у

| йк = у

НУ

, (VI. 13)

м, м*

136'

поскольку сумма элементарных превышений от М

до N дает отрезок нормали

ЛГ(Д, т. е. величину Подставив (VI.

13)

в (VI.12), получим

(уи4)

Среднее значение нормальной силы тяжести у

на отрезке М входя-

щее в (VI. 14), в соответствии с (У.44) вычисляется по формуле

V* = V. (1

зт

т*

2+ (У1.15)

Поскольку зависимость Н\

от

Ут весьма слабая, то при вычислении у

со-

гласно (VI.

15)

можно с пренебрегаемой погрешностью геодезическую широту

заменить астрономической, а вместо нормальной высоты взять ее приближен-

ное значение. Формула (VI.

14)

неудобна для практического применения.

Обычно ее преобразуют, выделяя главную часть и ряд небольших поправок.

Представим (VI.

14)

в виде

(VI. 16)

где ДН

— небольшая поправка за влияние гравитационного поля Земли,

учитывающее неравенство § у

Выделенная, таким образом, главная

часть нормальной высоты имеет простой геометрический смысл: | йк — сумма

измеренных превышений — величина, получаемая непосредственно в про-

цессе нивелирования. Введем обозначение

\ д,к = Н*$

, (VI. 17)

понимая под Нм" — измеренную высоту точки М. Следовательно, формулу

•VI. 16)

можно переписать

= Н^+АН

. (VI. 18)

Таким образом, полученная в результате измерений, производимых на

•физической поверхности Земли, разность потенциалов Ш

—Ц

позволяет

определить только составляющую геодезической высоты точки М, а именно —

нормальную высоту, очень близкую к сумме измеренных превышений.

Разность между геодезической высотой Н

точки М и ее нормальной

РЫСОТОЙ Нм, т. е. величина

'См = #м—

называется аномалией высоты и равна отрезку нормали N111, проведенной

к эллипсоиду в точке М (см. рис. 36). Ее можно рассматривать в качестве

второй составляющей геодезической высоты. Очевидно, что аномалии высот,

как и уклонения отвеса, характеризуют отступления гравитационного поля

Земли от нормального. Приведем вывод формулы, устанавливающей связь

между аномалией высоты и возмущающим потенциалом.

О способах вычисления этой поправки си. § 53 и 54.

ну

= \ АН

137'

В соответствии с (VI.

представим возмущающий потенциал Тм в точке М

физической поверхности Земли в виде

Т (В, Ь, Н) = №(В, Ь, Щ-И (В, Н).

Для получения нормального потенциала 17

в точке М воспользуемся

разложением в ряд

= ЩВ, Н)

— 11

(В, + . . •

Тогда

Т{В, ь, Н) = Ж{В, ь, Н)~и(в,

Полагая

| дЦ(В, НУ)

= — Уя

найдем

или

| дН т

эп(в, н?)

Лр

_. &*о(в, 0) ^ .

дВ ~дНУ~^дВ~

Т(В, Ь, Н) =

1У

(В, Ь, Н) —17 (В, +

Т (В, Ь, Н) = Ш

-\ —17 (В, +

Из условия, которое ставится при определении нормальной высоты, выте-

кает, что

-} = Н

) — V(В, 0) = #(#, Я

)-г/

Следовательно,

Т(В, Ь, = +

или

Тм = №

-1/

+ у^

Отсюда

= + (VI. 19)

УИ У&

где

V* = V. (1 +

Фм - р! зхп

фм

) + НУ

. (У1.20)

Формула (VI.19) устанавливает зависимость между аномалией высоты I

и возмущающим потенциалом в точке М.

Если параметры уровенного эллипсоида выбраны под условием соблюде-

ния равенства \У

= 17

, то выражение для аномалии высоты принимает более

простой вид

(VI.21)

Аномалии высот и нормальные высоты находятся в строгом соответствии

друг с другом: их сумма дает значение геодезической высоты точки М. На осно-

вании вышеизложенного получим

= + и = + {Тм + II

- ид. (VI.22)

138'

§ 32. КВАЗИГЕОИД

Рассмотрим вспомогательную поверхность, введенную М. С. Молоденским,

которая получила название квазигеоида. Представим себе, что от точки М

с координатами В, Ь, Н = 0, по направлению нормали к эллипсоиду отложена

величина аномалии высоты определенная в точке М. Тогда мы получим не-

которую точку К, координаты которой В, Ь и ^ (см. рис. 36). Если этот процесс

продолжить для каждой точки физической поверхности Земли, то в результате

получим множество точек К, совокупность которых и образует поверхность о',

названную Молоденским квазигеоидом. Высоты квазигеоида над эллипсоидом

будут равны аномалиям высот, определенным в точках физической поверх-

ности Земли. Высоты точек М над поверхностью а' квазигеоида совпадают

с нормальными высотами.

Следовательно, нормальную высоту можно определить как высоту точки

физической поверхности Земли над поверхностью квазигеоида.

На океанах нормальные высоты равны нулю и потому геодезическая вы-

сота Н точки М, находящейся на поверхности океана, равна высоте квази-

геоида Отсюда следует, что на океанах квазигеоид совпадает с уровенной

поверхностью потенциала силы тяжести (геоидом) = \У

. На материках

эти две поверхности незначительно отличаются друг от друга. Так, по исследо-

ваниям В. Ф. Еремеева, в равнинных районах отступления квазигеоида от

геоида по высоте составляют величину нескольких сантиметров и только в горах

могут достигать величины около 2 м. Поэтому практически поверхность квази-

геоида может рассматриваться в качестве «уровня моря», относительно которой

даются высоты на топографических картах.

Поверхность квазигеоида имеет сложную форму, отражающую сложный

характер гравитационного поля Земли. Поскольку высоты квазигеоида

'С,

могут

быть как положительными, так и отрицательными, поверхность квазигеоида

может и подниматься, и опускаться относительно уровенного эллипсоида, т. е.

эта поверхность образует волны различной протяженности и амплитуды.

Чтобы убедиться в этом, представим величину I, в виде разложения по

шаровым функциям. Подставив (VI.4) в (VI.21), получим

(VI.23)

Таким образом, величину поднятия или опускания квазигеоида в произ-

вольной точке можно представить суммой бесконечного числа гармоник.

Но каждая гармоника имеет свою амплитуду колебаний и отражает коле-

бательные процессы лишь в соответствии с заданной для нее функциональной

зависимостью от координат 0 и Я. Поэтому характер волн, представляемых

различными гармониками, неодинаков. Так, например, зональные гармоники

четной степени дают волны, расположенные симметрично относительно эква-

тора (см. рис. 22, 24), тогда как зональные гармоники нечетной степени (см.

гнс. 23) характеризуют противоположный эффект в северном и южном полу-

шариях сферы. В свою очередь, секториальные (см. рис. 25, 26) и тессеральные

см. рис. 27, 28, 29) гармоники представляют колебания, являющиеся функ-

циями не только широты, но и долготы.

Естественно, что сумма различных гармоник в (VI.23) дает очень сложный

закон, которому подчиняются изменения величины I,.

(9, X)

139'