Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Высота квазигеоида

связана с возмущающим потенциалом, определяемом

в точках физической поверхности Земли (VI.19). Так как возмущающий потен-

циал является непрерывной и однозначной функцией, то этими же свойствами

обладает и высота квазигеоида. Следовательно, поверхность квазигеоида

является непрерывной и определяется однозначно. Однако возмущающий

потенциал Т связан с поверхностью, на которой он определяется, поэтому

естественно предположить, что если его определять пе на физической поверх-

ности Земли, а на какой-то иной поверхности, то этой, иной поверхности будет

соответствовать свой квазигеоид. Ведь в принципе возмущающий потенциал

является функцией высоты точки над поверхностью эллипсоида и если его

определять в точках, лежащих на разных высотах, но на одной отвесной линии,

то для каждой из них будет существовать своя аномалия высоты и, следова-

тельно, разные высоты квазигеоида. Но во всех этих случаях квазигеоиды не

имеют физической интерпретации.

Рис. 37

Возможен, однако, реальный случай, когда необходимо рассматривать

два квазигеоида, например, при геодезических работах, проводимых в шахтах

и туннелях. Высота квазигеоида для точки М физической поверхности Земли

вычисляется по формуле (VI. 19)

м ^ Ц

~УУр

а высота квазигеоида для точки Ь, находящейся в шахте,

г -

?ь

<>-

ЬЬ у "Т у •

Поскольку Т

Ф заключаем, что См Ф Геодезические высоты

точек М и Ь с высотами квазигеоида связаны соотношениями

#3и

поэтому

МЬ = Н

-Н

= Щ, — Я* +

(См

- Ы-

Но См Ф

Ъъ

и поэтому Н

-Н1Ф МЬ.

Таким образом, если из нивелирования определить нормальные высоты

точек М и Ь, то их разность не будет равна глубине точки Ь относительно

физической поверхности Земли.

140'

В этом случае В. Ф. Еремеев предлагает определять геодезические высоты

точек, находящихся внутри Земли, через высоты соответствующих точек земной

поверхности. Так, например, для точки Ь (рис. 37) можно использовать соотно-

шение

Яь-ДЪ + С*--^-.

~г8 Т. пгт

где §

ср

= ^ среднее значение силы тяжести на отрезке МЬ.

Разность потенциалов — IУм можно определить с помощью геометри-

ческого нивелирования, сопровождаемого измерениями силы тяжести в точках

нивелирного хода.

§ 33. ВОЗМУЩАЮЩИЙ ПОТЕНЦИАЛ И ФИГУРА ЗЕМЛИ

Проблема изучения фигуры Земли непосредственно связана с задачей

определения возмущающего потенциала, поскольку составляющие уклонения

отвеса и аномалии высот, вычисленные через возмущающий потенциал (фор-

мулы (VI.8) и (VI.19), позволяют получить точные геодезические координаты В,

Ь и Я всех пунктов триангуляции относительно принятого уровенного эллипсо-

ида V = Цо. _

Если В и Ь первоначально установленные геодезические координаты пунк-

тов триангуляции, то после определения составляющих уклонения отвеса | и

по формулам (VI.8) можно получить точные значения координат ВаЬ путем

введения соответствующих поправок б В и 8Ь.

Геодезические координаты и составляющие уклонения отвеса на основании

формул (VI.5) связаны между собой соотношениями

Д = Ф—| — АВ)

г , • (У1.24)

Ь =

— 11созф )

Следовательно, в исходном пункте триангуляции первоначальные коорди-

наты были получены по формулам

^о =

Фо

— &

о'>

~Ё-о

Хо

— 'Позесфо,

где |

и т]

— составляющие уклонений отвеса в исходном пункте триангуля-

ции, полученные из градусных измерений. После того, как будут вычислены

через возмущающий потенциал [по формулам (VI .8)] точные значения соста-

вляющих уклонений отвеса | и т), можно получить в исходном пункте и точные

геодезические координаты В

и Ь

= В

+ 8В

;

= Ь

+ б Ь

;

бВ

= — 2

;

141'

Затем могут быть вычислены поправки бВ

и бЬ

в координаты каждого

1-го пункта триангуляции. В том случае, если координаты пунктов триангуля-

ции даны в какой-либо другой (местной) системе, то при вычислении попра-

вок ЬВ и ЬЬ необходимо учитывать не только изменение координат исходного

пункта, но и изменение параметров эллипсоида (большого полуоси и сжатия).

Подробнее этот вопрос излагается в § 77.

Таким образом, можно получить в единой системе точные значения коорди-

нат В и Ь всех пунктов сетей триангуляции.

В том случае, когда точка М земной поверхности не является пунктом

триангуляции, ее координаты В и Ь можно вычислить через астрономические

координаты ф и X по формулам

А дТ й

= Фм + - А^рг

ЗШ

2В

, (У1.25)

Ьм = Хм+

уД соз2 в 8

п1

. ~~. (У 1.26)

Геодезическая высота Н

при этом находится по формуле (VI.22).

Глава VII

АНОМАЛИИ СИЛЫ ТЯЖЕСТИ И ИХ

ИСПОЛЬЗОВАНИЕ В ГЕОДЕЗИИ И ГЕОФИЗИКЕ

§ 34. ПОНЯТИЕ ОБ АНОМАЛИЯХ СИЛЫ ТЯЖЕСТИ.

АНОМАЛИЯ В СВОБОДНОМ ВОЗДУХЕ

Аномалией силы тяжести называют разность между действительной силой

тяжести (полученной из наблюдений) и ее нормальным (теоретическим) значе-

нием. Аномалия силы тяжести называется «чистой» в том случае, если значения

действительной силы тяжести и нормальной отнесены к одной и той же точке,

если же эти значения относятся к разным точкам пространства, аномалия назы-

вается «смешанной».

Поскольку, как правило, имеет место последняя ситуация, возникает

необходимость при вычислении аномалий силы тяжести, либо в значение изме-

ренной силы тяжести, либо — нормальной, вводить поправки, называемые

редукциями.

В зависимости от того, какие поправки (редукции) вводятся, различают

разные виды аномалий.

Аномалией в свободном воздухе (^ — у)

св

называют разность

(*—?)«. в. = ем = (То + А?), (VII. 1)

где §м — значение измеренной силы тяжести в точке М; у^ — значение нор-

мальной силы тяжести в точке N (см. рис. 36); у

— значение нормальной силы

тяжести на уровенном эллипсоиде в точке М

; Ау — поправка за высоту.

На основании формул (У.32), (У.34) и (У.39) имеем

Ау — — 0,30855 (1 + 0,00071 соз 2 В) № + 0,0723 (В*)*-10"

. (УИ.2)

Если нормальная высота задана в метрах, поправка Ау согласно (VII.2)

определяется в миллигалах.

Таким образом, при вычислении аномалий в свободном воздухе в измерен-

ное значение силы тяжести § поправки не вводятся.

Вычисленная по формулам (VII.1) и (VII.2) аномалия в свободном воздухе

будет «смешанной».

Поправка Ау за высоту, вводимая в нормальное значение силы тяжести,

называется редукцией в свободном воздухе. Это название связано с тем, что

приведение силы тяжести в нормальном поле по формуле (У.32) предполагает

отсутствие вне эллипсоида притягивающих масс (первоначально притяжением

воздуха просто пренебрегали). В этом смысле редукцию в свободном воздухе

было бы лучше назвать редукцией в пустоте.

143'

Аномалия в свободном воздухе может быть и «чистой» аномалией. В этом

случае вместо нормальной высоты Н

при вычислении редукции Ду [формула

(VII.2)] следует взять геодезическую высоту Н. Однако до последнего времени

«чистые» аномалии в свободном воздухе при исследованиях фигуры Земли

не применялись.

В условиях дискретной гравиметрической съемки для определения ано-

малий в промежуточных пунктах, где наблюдений силы тяжести не производи-

лось, появляется необходимость в интерполировании аномалии.

Аномалии в свободном воздухе существенно зависят от рельефа местности

и потому линейное интерполирование этих аномалий приводит к неудовлетво-

рительным результатам. Поэтому обычно применяется так называемое косвен-

ное интерполирование аномалии в свободном воздухе, используя при этом

другие виды аномалий.

Основной причиной, вызывающей сложный, неправильный характер изме-

нения аномалий в свободном воздухе, является действие притягивающих масс,

находящихся между физической поверхностью Земли и уровнем моря

(назы-

ваемых топографическими массами). Если из аномалий силы тяжести исключить

влияние топографических масс, то линейное интерполирование полученных

таким образом аномалий дает более удовлетворительные результаты. С необ-

ходимостью устранения возмущающего эффекта топографических масс из

результатов наблюдений силы тяжести приходится встречаться и при решении

различных геологических проблем, в частности при разведке полезных иско-

паемых, а также при изучении внутреннего строения Земли. Гравитационные

аномалии можно считать обусловленными действием наружных топографи-

ческих масс и аномальных масс, находящихся внутри Земли. Для геологи-

ческой интерпретации результатов гравиметрических определений разделение

этих двух влияний имеет важное значение. Аномалия должна быть обусловлена

притяжением только тех масс, которые представляют интерес при решении

данной проблемы и, следовательно, все другие влияния должны быть исклю-

чены.

Поправку за влияние притягивающих масс, заключенных между уровнем

моря и физической поверхностью Земли, будем называть топографической

поправкой (редукцией) или, иначе, поправкой (редукцией) за топографию.

Топографическая поправка представляет собой вертикальную составляющую

притяжения топографических масс и в соответствии с формулой (1.11) опре-

деляется из соотношения

где г — радиус-вектор от притягивающей точки до текущей элементарной

массы дт\ (г, г) — угол между радиус-вектором и положительным направле-

нием оси г в притягиваемой точке (обычно ось 2 совмещается с направлением

отвесной линии); х — полный объем топографических масс.

Уровнем моря здесь и везде далее будем считать поверхность квазигеоида. Под высо-

той точки земной поверхности над уровнем моря будем понимать ее нормальную высоту Н

но в дальнейшем изложении для упрощения обозначений индекс у будет опущен.

§ 35. ТОПОГРАФИЧЕСКИЕ РЕДУКЦИИ

(УИ.З)

144'

Под топографическими массами будем понимать все массы, расположенные

выше уровня моря, имеющие, как правило, переменную плотность б, дополни-

тельные массы в континентальных депрессиях ниже уровня моря, имеющие

плотность, равную средней плотности земной коры б

= 2,67 г-ему"

, и до-

полнительные океанические массы, имеющие плотность б" = 8' — б

, где б' =

= 1,03 г-см""

— плотность морской воды.

Следует заметить, что на море топографические редукции при использова-

нии аномалий силы тяжести в геодезических целях для улучшения интерполя-

ции малоэффективны, поскольку неровности дна удалены от гравиметрического

пункта, расположенного на поверхности моря и обычно малоизвестны. Для

решения геодезических задач достаточно удалить топографические массы,

расположенные лишь выше уровня моря. Топографическая редукция может

включать эффект всех топографических масс Земли и тогда она называется

полной топографической редукцией. При вычислениях полной топографической

редукции влияние дальних зон может быть вычислено с помощью ЭВМ, с ис-

пользованием средних высот по стандартной сетке или разложения высот по

сферическим функциям. Как правило, однако, влияние топографических масс

учитывается только до определенного расстояния от точки наблюдения и в этом

случае поправка называется неполной топографической редукцией. Выбор

расстояния, в пределах которого должно быть учтено влияние топографических

масс, зависит от многих обстоятельств: высоты точки наблюдения над уров-

нем моря, общей формы местности, величины эффекта удаленных масс и,

наконец, специфики решаемой задачи.

При вычислении топографических редукций вводятся некоторые

упрощения. Вместо эллипсоида рассматривается сферическая модель

Земли, а при небольших радиусах учитываемого района — даже плоская

модель.

Вся поверхность земного шара делится концентрическими окружностями,

проведенными вокруг точки наблюдения, на зоны, которые в свою очередь

радиальными лучами делятся на секторы, в которых средняя высота местности

(или глубина морского дна) должна быть известна. Действительная форма

топографических масс, таким образом, представляется системой призмати-

ческих тел. Ближайшие к наблюдаемой точке зоны могут рассматриваться как

плоские, влияние остальных зон должно производиться с учетом сферичности

Земли. Примером подобного разделения поверхности Земли может служить

способ деления на зоны и секторы, предложенный американским геодезистом

Хейфордом. Хейфорд разбил всю поверхность Земли на 15 плоских зон, обозна-

ченных латинскими буквами от А до О (внешний радиус последней плоской

зоны 0

принят равным 166,7 км) и на 18 сферических, которые обозначены

номерами от 18 до 1 (1 зона — самая отдаленная). Границы каждой сферической

зоны установлены таким образом, чтобы редукция при заданной высоте к в пре-

делах сектора равнялась 0,1 мгл. Внешний радиус последней плоскости зоны

равен внутреннему радиусу сферической 18-й зоны. Таким образом, вся Земля

без пробелов покрыта 33 зонами. Внешние радиусы зон и число секторов в каж-

дой зоне даны в табл. 4.

Предложенное Хейфордом деление поверхности Земли на зоны и секторы

до сих пор используют при вычислениях редукций, для чего составлены спе-

циальные таблицы, при помощи которых определяют влияние топографических

масс всей Земли на величину силы тяжести в данной точке.

Для вычисления топографической редукции определяют притяжение топо-

графических масс, расположенных в каждом секторе всех зон как плоских,

50 Заказ 1379

145

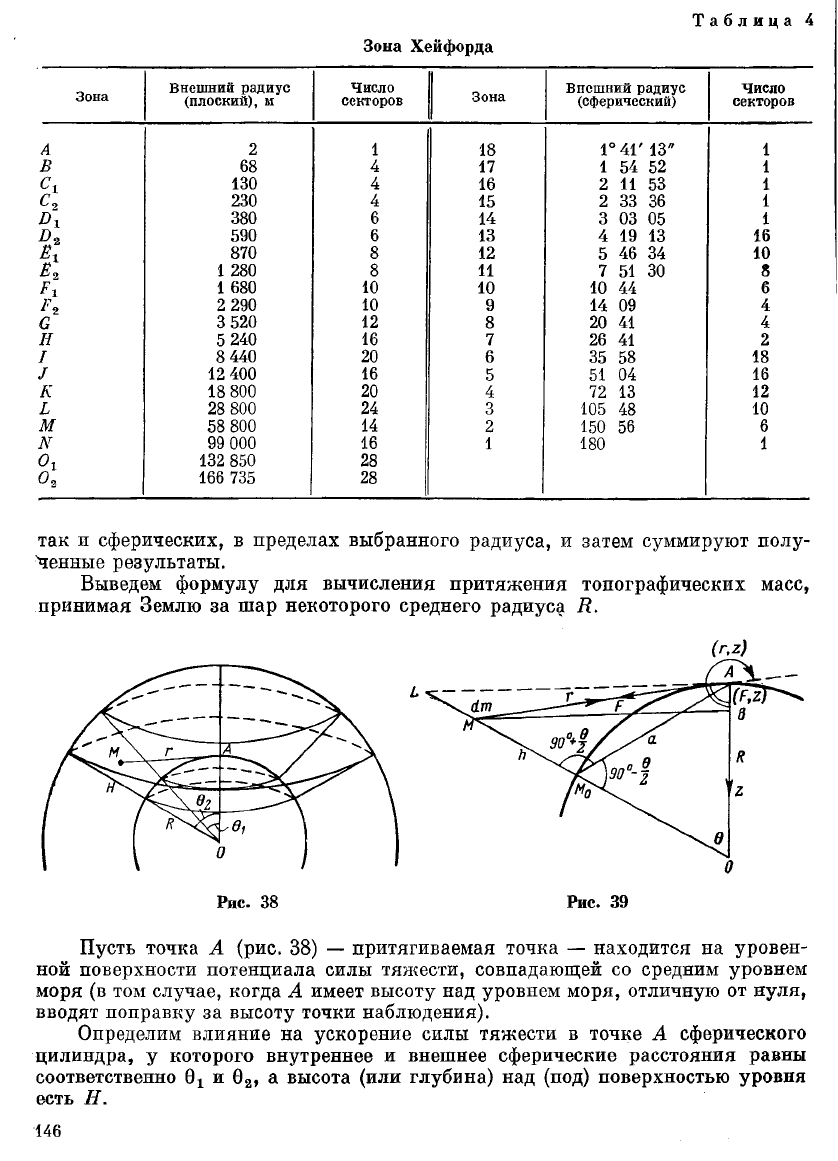
Таблица 4

Зона Хейфорда

Зона

Внешний радиус

(плоский), м

Число

секторов

Зона

Впешний радиус

(сферический)

Число

секторов

А 2

1° 41' 13" 1

1 54 52 1

Сх

130 4

2 11 53 1

С,

230

2 33 36

Ох

380 6 14

3 03 05 1

590 6 13

4 19 13

Ёг

870 8 12

5 46 34

1 280 8 11

7 51 30

Рг

1 680 10

10 10 44

Г*

2 290 10 9

14 09

3 520

8 20 41

и 5 240 16 7 26 41 2

8 440

20 6

35 58

12 400 16

5 51 04

к 18 800 20

4 72 13

28 800

24 3

105 48 10

58 800

150 56

N 99 000 16

180

Ог

132 850

О 2

166 735

так и сферических, в пределах выбранного радиуса, и затем суммируют полу-

денные результаты.

Выведем формулу для вычисления притяжения топографических масс,

принимая Землю за шар некоторого среднего радиуса Е.

(г.*)

Пусть точка А (рис. 38) — притягиваемая точка — находится на уровен-

ной поверхности потенциала силы тяжести, совпадающей со средним уровнем

моря (в том случае, когда А имеет высоту над уровнем моря, отличную от нуля,

вводят поправку за высоту точки наблюдения).

Определим влияние на ускорение силы тяжести в точке А сферического

цилиндра, у которого внутреннее и внешнее сферические расстояния равны

соответственно 9

и 0

, а высота (или глубина) над (под) поверхностью уровня

есть Н.

146'

Считая объемную плотность б постоянной и выражая элемент объема в сфе-

рических координатах

Ах

= (К ± к)

зт

Э Й0 АХ

Ак,

в соответствии с формулой (VII.3) получим

Н 0

2Я

= —/6^ С

008г)

(Д±&)

зш9<*9ДД.аЛ.

о 91 о

где г — расстояние текущей точки М от притягиваемой точки А; к — высота

точки М над сферической поверхностью уровня; 0 и А, — сферические коорди-

наты точки М.

Совместим ось г с направлением отвесной линии в точке А (рис. 39). Учи-

тывая, что направление силы Р, с которой элементарная масса Ат, находящаяся

в точке М, притягивает точку А, противоположно направлению вектора г,

получим

— соз (г, г) = соз (Р, г). (VII.4)

Из треугольников МАВ и ММ

А находим

соз (Р,

г)

= — = ,

Обозначив

г* =

+ к

+2ак зт-|-.

• к

соз 0

С0Я(Л«)_ 2Л = Е (к, 0),

(а2 + й2+2а/г 81П-|")

получим

02 2Я

А^ = /6 | | \ Е (к, 0) (.К ± ку зт 0

<26 АХ

Ак. (УИ.5)

01 О

Найдем среднее значение функции Е (к, 0) для данного цилиндра

Ё = Е

ср

(к, 0).

Тогда

н е

2я

О 01 О

или после интегрирования

А^ = 2к/бЕ*Н + (соз0

соз0

)Е.

Отбрасывая из-за малости поправочные члены, найдем окончательно фор-

мулу для вычисления вертикальной составляющей притяжения сферического

цилиндра (топографическую редукцию, обусловленную притягивающими мас-

сами, заключенными внутри данного цилиндра) в наблюдаемой точке А

Ад = 2я/бНт (соз 0

—соз

)

Ё. (УН.6)

10* 147

Вычисление среднего значения функции Е (к, Э) величин Е представляет

значительные трудности, поэтому поступают иначе. Сохраняя малые второго

порядка, представим функцию Е (к, 0) в виде

д2

•

ксоз0

27/7 пч 2Я " /1 к

\/. . 2к . 0 V

"Ч

18Ш

т)

7 2

3 к . в

-СОЗ У т ГТГ-81П

2аЛ «з ~ 2 аЩ 2

Образуем произведение Е зт 0, заменив а через 2Е

З1п

2 кГ 8 0 9 "1

Е(к, 0)зт0--2д2 -^[гсоз-^ + с^-^-соа^

я подставив это значение в (VII.5), после интегрирования по 0 и к найдем

= 2я/бя(зтА_зт (3 зт созес

- 3 зт - созес (УП.7)

Формула (VII.7) более удобна для вычисления влияния далеких притяги-

вающих масс, имеющих форму цилиндрического пояса, на величину силы тя-

жести в точке А, чем (VII.6). Для вычисления топографической редукции за

притяжение топографических масс, расположенных в пределах одного сектора

данной зоны, следует использовать формулу

Д 2я/6Я I . 09 . 01 \ я/б ГГ2 / о - 01 , 01

А* = —г— (зт -- - зт - Н* (3 зт созес -

— Ззт-^- — созес -у-)» (УН.8)

где п — число секторов в данной зоне.

При расстояниях от притягиваемой точки порядка до 200 км можно пре-

небречь кривизной Земли и рассматривать земную поверхность как плоскость.

В этом случае формулы для вычисления топографической редукции значительно

упрощаются.

На основании формулы (VI 1.3) и соотношения (VI

1.4)

получим

2Я

ООО

где а — радиус района, Я — высота точек земной поверхности над уровнем

моря. В общем случае Я = / (I, а) — будет переменной величиной.

Выберем цилиндрическую систему координат (рис. 40). Начало координат

совместим с точкой А

, за ось

т.

примем направление отвесной линии в точке А.

Тогда координатами текущей точки М, где находится элементарная масса дт,

будут: I — радиус-вектор, а — полярный угол иг — высота точки М над

уровнем моря. Выразим элемент объема йх в выбранной системе координат

йх =

1й1

йа йг.

448'

Из треугольника ЬАМ находим

сов

(Р, г)

•

отсюда

С08 (Р, 2) к

-{-Н—-я

,•2

2Я

а Н

(йр

+ Я - г)

[г2+(А

+ я-

)2]

г/г

ООО

В результате интегрирования по г получим

2Я а

г г

]/'

г2+

(й

+Я)2

д,Ыа. (VII.9)

Чтобы выполнить дальнейшее интегрирование, необходимо знать вид

функции Н = / (I, а) по всей учитываемой поверхности. Вид этой функции

определяется при помощи топографической карты. Вся местность, подлежащая

учету, разбивается по тому или иному закону на отдельные ячейки.

Рве. 41

Уровень

моря

Рис. 40

Можно, например, для этого воспользоваться системой концентрических

окружностей и радиально расходящихся лучей (рис. 41). Размеры радиусов

кольцевых зон, а также число ячеек в каждой зоне определяются условиями

местности. Очевидно, что в пределах каждой отдельно взятой ячейки найти

вид функции Н = / (I, а) при помощи топографической карты значительно

проще, чем для всего учитываемого района. Размеры ячеек следует выбирать

настолько малыми, чтобы внутри каждой отдельной ячейки высоту Н можно

было считать постоянной, равной средней высоте. Влияние такой ячейки с номе-

ром I на величину силы тяжести в точке А согласно (VI 1.9) будет

1+1

= /8

С Г Г .

}йЫа, (VII. 10)

149'