Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Если в подынтегральной функции (1.20) вместо г подставить г

га1п

или г„

(рис. 13), то, очевидно, будут иметь место следующие неравенства:

шах

Н'К'Ш'

йт

Но г

тах

и г

т!п

, как постоянные величины, могут быть вынесены из-под

знака интеграла, а интеграл

где М — масса тела.

В результате получаются неравенства

' тах ' тт

которые после умножения на г принимают вид

и^

<гУ(Р)<

1т..

тах ' т!п

При удалении точки Р в бесконечность

Нш ——=Нш ——= 1.

тах г щ1п

Отсюда получаем, что

НтгУ = /М. (1.74)

г->-со

Аналогично можно доказать, что

дУ

Нт

г-> оэ

дг

--1М.

Функция, удовлетворяющая полученным трем условиям (1.73), (1.74)

и (1.75), называется регулярной на бесконечности. Потенциал объемных масс

регулярен на бесконечности.

Потенциал простого слоя

Аналогично тому, как это было доказано для потенциала объемных масс,

можно доказать, что потенциал простого слоя непрерывен и конечен во всем

пространстве, вне притягивающих масс удовлетворяет уравнению Лапласа

и имеет непрерывные производные всех порядков, на бесконечности является

функцией регулярной.

Производная потенциала V по произвольному направлению I

ТГ-'И (1.76,

а а

является проекцией силы притяжения простого слоя на направление I. В том

случае, когда притягиваемая точка пересекает поверхность простого слоя,

первые производные потенциала терпят разрыв. Мы уже убедились в этом при

рассмотрении частного случая простого слоя — бесконечно тонкого однород-

ного сферического слоя (см. § 4). Теперь покажем, что это имеет место и в более

общем случае.

Обозначим внешнюю точку относительно слоя через А, внутреннюю —

через В, а точку на самой поверхности слоя — через С (рис. 14). Пусть точки А

В неограниченно приближаются к точке С, в этом случае производные потен-

циала У по произвольному напра-

иметь различные

влению I будут

пределы.

Будем называть внешней произ-

водной потенциала простого слоя

в точке С величину

Н46

А1

Нт

А-уС

ау

А1

= —Нт / СС

А-УС «>

[ХС08(Г

, I)

йа (1.77)

Рис. 14

внутренней производной потенциала простого слоя в точке С величину

аУс

= Нт

в-+с

6У

А1

-Нт / СС

(х

соз (г

, I)

йа.

(1.78)

Следовательно, внешнюю и внутреннюю производные можно определить

как пределы, к которым стремится составляющая силы притяжения простого

слоя по направлению I при неограниченном приближении притягиваемой точки

к слою с внешней и внутренней сторон поверхности а.

Прямое значение производной —йУ^/й/ определим, как составляющую

силы притяжения в самой точке слоя. йУ^'/й/ определяется без предельных

переходов непосредственно в точке С, расположенной на слое

АУ$

6,1

-'И

Р СОВ

(Г

йа.

(1.79)

Для того чтобы показать, что при приближении текущей точки М к точ-

кам С, А и В (а точки А и В неограниченно приближаются к точке С), т. е.

когда г будет стремиться к нулю, интегралы в (1.77) (1.78) и (1.79) сохранят

конечное значение, поступим следующим образом. Выделим вокруг точки С

бесконечно малый круг а

с постоянной плотностью рс- Тогда все три произ-

водные можно будет представить в виде сумм

ЛУе

<11

АУУ

- Нт

А-+С

/П

с-СГо

= — Нт / СГ

В-+С ^ ^

О-Оо

|ЛС03(Г

, I)

(X СОЗ

(Г

)

'в

соз (г

)

йа- Нт

А-^-С

цсоз(г

, I)

йа,

йа — Нт /ГС

Г р,С08(г

, I)

йа-

•'Н

йа,

Ов

ЦС08(г

, г)

йа.

(1.80)

(1.81)

(1.82)

Первые слагаемые в формулах (1.80), (1.81) и (1.82) всегда ограничены,

так как в области о — сг

г нигде не обращается в нуль.

При совпадении точек А и В с точкой С будут иметь место равенства

Нт

А^-С

о-а.

цсо8(г

, I)

йа = Нт

в^с

о-о„

ЦС08(/-

, I)

-йа

[.1С08(г

, I)

йа. (1.83'

Вторые слагаемые в (1.80), (1.81) и (1.82) можно рассматривать как соста-

вляющие притяжения плоского круга сг

по направлению I.

Значения этих составляющих определяются по формулам (1.63), следует

только заменить в них направление оси

т,

направлением внешней нормали п

к поверхности а в точке С. Подставляя (1.63) в (1.80), (1.81) и (1.82) и считая,

что круг а

стремится к нулю, в пределе получим

4У^

^ цсоз(г

, I)

си

йУк

А\

-'И

ЦС08(г

, I)

(Д,С08(/'

, I)

йа — 2я/р

соз (п, I)

йа-|-2я/р

соз (п. I)

йа

(1.84)

или опуская индексы С,

4У

ау о

йУ{

4У(1

•2я/рсоз (п, I)

-р2я/рсоз (п, I)

Отсюда получим

41 41

4У

1 V 4У

. 4У1

1 Г4У

4УГ1

2 [_ 41 ' 41 _Г

(1.85)

(1.86)

Эта формула называется формулой Плёмели. Пользуясь формулой Плёмели,

мояшо получить прямое значение производной на слое йУ

/й1 через предельные

значения.

Вычитая из первого соотношения в (1.85) второе, получим формулу Пуас-

сона

4У

АУ,

41 41

-4я/рсоз(и, I).

(1.87)

Формула Пуассона позволяет вычислить величину скачка производной

потенциала простого слоя при пересечении притягиваемой точкой поверх-

ности слоя.

Если производную потенциала брать по направлению внешней нормали

к поверхности слоя, то соз (п, I) = +1 и получим

4У

4УI

4п

—4я/р.

(1.88)

Итак, первые производные потенциала силы притяжения простого слоя терпят

разрыв при пересечении слоя. Поэтому па простом слое всегда следует раз-

личать три значения производных потенциала: два предельных и одно прямое.

Потенциал двойного слоя

Потенциал двойного слоя можно представить как сумму производных

иенциалов простых слоев (1.33). В самом деле, интегралы, стоящие справа

1.33), являются потенциалами простых слоев с плотностями —V сов (п, х),

-V соз (п, у) и —V соз (п, г).

Во внешнем пространстве производные потенциала простого слоя непре-

^вны, удовлетворяют уравнению Лапласа (1.70) и регулярны на бесконеч-

:сти. Следовательно, во внешнем пространстве этими свойствами будет обла-

сть и потенциал двойного слоя.

Однако при пересечении притягиваемой точкой поверхности слоя первые

:оизводные потенциала простого слоя терпят разрыв, поэтому и потенциал

ЕОЙНОГО слоя также будет терпеть разрыв. Так же, как и для первых произ-

лных потенциала простого слоя, следует различать два предельных 1У

и И

олно прямое значение Ш

потенциала двойного слоя. Величина разрыва

: генциала двойного слоя в точках самого слоя определяется из соотношений

1У

= 1У

+ 2я/у

(1.89)

§ 6. УГОЛ ВИДИМОСТИ И ИНТЕГРАЛЫ ГАУССА

Если двойной слой имеет постоянную плотность /V = 1, то его потенциал

:>значим через Й. В этом случае формула (1.30) примет вид

„ .

Г Г

соз (г, п)

Я (г, =

• йа.

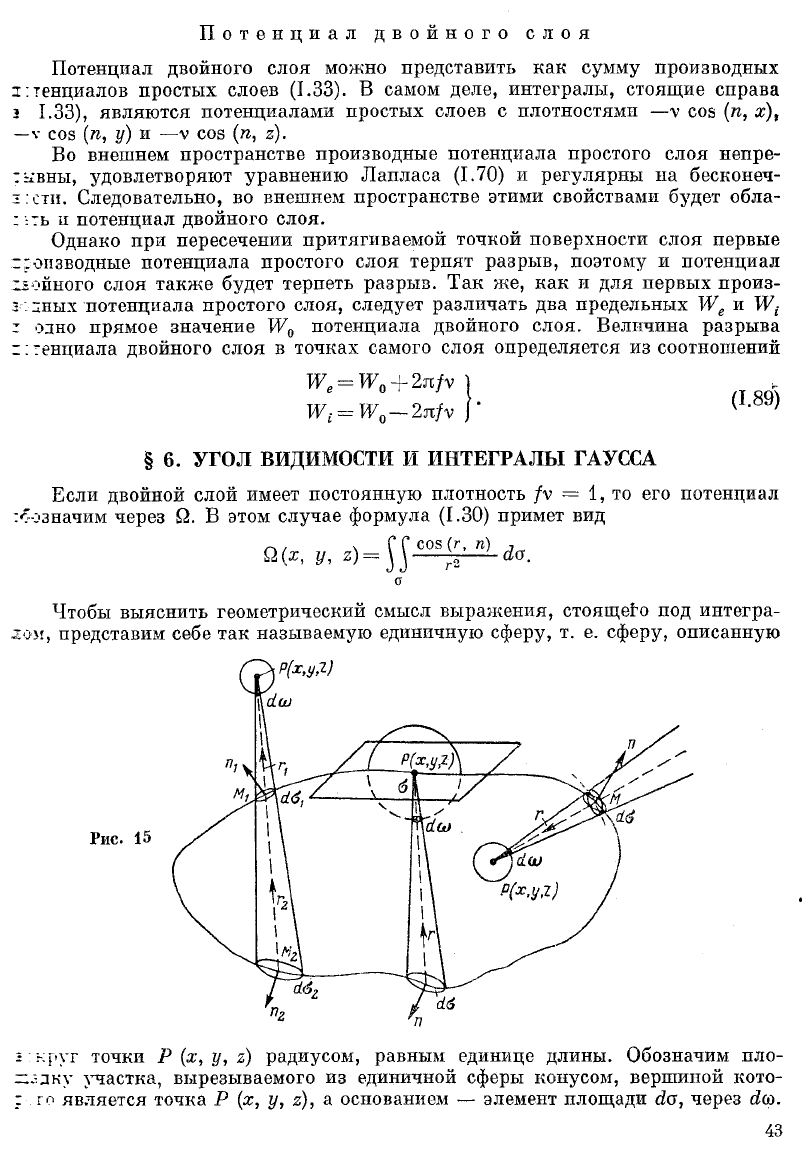
Чтобы выяснить геометрический смысл выражения, стоящего под интегра-

ом, представим себе так называемую единичную сферу, т. е. сферу, описанную

Рис. 15

круг точки Р (х, у, 2.) радиусом, равным единице длины. Обозначим пло-

.^дку участка, вырезываемого из единичной сферы конусом, вершиной кото-

го является точка Р (х, у, г), а основанием — элемент площади йа, через й<л.

Величина йа называется элементарным телесным углом или же углом види-

мости, под которым элемент йа виден из точки Р. Для вычисления йен необхо-

димо элемент йа поверхности а в точке М (рис. 15) спроектировать на сферу

с центром в точке Р и радиусом г, что даст йа соз (г, п), и поделить на г

, так что

Ла

соз (г, п)

= —^—>-.

При этом йа нужно брать с положительным или отрицательным знаком,

смотря по тому, образует ли вектор г острый или тупой угол с направлением

внешней нормали п к поверхности а.

Вычислим значение потенциала & в трех точках: внутренней относительно

замкнутой поверхности а, внешней и на самой поверхности а.

На основании предыдущего можно написать

(ж,

у, = а.

сг

Если потенциал вычисляется внутри поверхности а, то соз (г, п) во всех

точках поверхности сг будет отрицательным (см. рис. 15) и потому

с/0 соз (/•, п)

Г 2

—йа.

Сумма углов видимости, под которыми площадки йа усматриваются из

точки Р, равна 4л и, следовательно,

й(ж, у, г) = — 4я.

Если потенциал вычисляется во внешней относительно поверхности а

точке Р (х, у, т), то каждый элементарный конус, вершиной которого является

точка Р, вырезает на этой поверхности два элемента: йа

и йа

(см. рис. 15),

причем угол между вектором г и внешней нормалью п будет острым в точке М

и тупым в точке М

. Следовательно, проекции элементов йа

, йа

на единичную

сферу будут равными по величине, но противоположными по знаку. Поэтому

-^р-соз^!, т^) -(- соз (гс

, г

) =

йсо

— йа = О,

где г

= М

Р, г

= М

Р (см. рис. 15).

Таким образом, для внешней точки получаем

Й(ж, у, 2) = 0.

При вычислении потенциала в точке Р, находящейся на самой поверх-

ности а, будем иметь (см. рис. 15)

с!а соз (г, п) ,

—= — йа,

а сумма элементарных углов видимости будет равна 2л, т. е. углу, под которым

из точки Р просматривается полусфера, лежащая по одну сторону от каса-

тельной к поверхности сг в точке Р.

Следовательно,

О (х, у, г) = —2я.

Полученные интегралы, определяющие значение потенциала двойного слоя

О (х, у, г) в различных точках, называются интегралами Гаусса. Как видно из

предыдущего, интеграл Гаусса О (х, у, г) испытывает скачок, равный -)- 4л, при

перемещении точки Р (х, у, г) изнутри наружу любой замкнутой поверхности а.

Глава II

КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ ПОТЕНЦИАЛА

§ 7. ФОРМУЛЫ ГРИНА

Прямая задача теории потенциала заключается в определении потенциала

тяготения V, если известны строение тела и его форма.

Для целей геодезии необходимо решить обратную задачу, состоящую

в определении формы притягивающего тела через его потенциал.

При этом важно исключить плотность б тела, поскольку в настоящее время

строение Земли, как и других тел солнечной системы, точно неизвестно. Можно

ли в принципе определить потенциал V, не зная закона распределения плот-

ностей внутри тела? Чтобы ответить на поставленный вопрос, необходимо

рассмотреть зависимость между потенциалом V и плотностью б.

В прямой задаче теории потенциала эта зависимость определяется фор-

мулой (1.20). Эта формула не позволяет дать положительный ответ на поста-

вленный вопрос.

Но рассмотрим обратную задачу: выразим плотность через потенциал.

Эта задача может быть решена с помощью уравнения Пуассона

ДУ = — 4я/6.

Левую часть этого уравнения всегда можно вычислить, если потенциал V

известен, и тем самым будет определена плотность в любой точке тела.

Поскольку уравнение Пуассона справедливо только внутри тела, следует

заключить, что плотность может быть выражена только через потенциал, задан-

ный внутри притягивающих масс.

А можно ли определить плотность тела в случае, если потенциал известен

только во внешнем пространстве? Если бы внешний потенциал можно было бы

аналитически продолжить внутрь притягивающих масс, то тогда плотность

тела была бы определена. Однако эта операция невозможна, потому что вну-

тренний и внешний потенциалы выражаются разными аналитическими функ-

циями. Можно найти бесчисленное множество различных распределений плот-

ности внутри тела при одинаковом внешнем потенциале.

Рассмотрим в качестве примера однородный шар. Как видно из формулы

(1.54), его внешний потенциал определяется массой М и, следовательно, при

любых значениях плотности б и радиуса Я, при условии, что общая масса

остается неизменной, внешний потенциал V будет иметь одинаковые значения.

Потенциал вне притягивающих масс удовлетворяет уравнению Лапласа,

которое не содержит плотности. Для его решения необходимо знать область,

в которой потенциал удовлетворяет уравнению Лапласа.

Таким образом, задача определения фигуры притягивающего тела непо-

средственно связана с определением внешнего потенциала, который может быть

найден независимо от плотности в результате интегрирования дифференциаль-

ного уравнения Лапласа.

В основе современных методов решения уравнения Лапласа лежат фор-

мулы преобразования некоторых объемных интегралов в интегралы по поверх-

ности, полученные Грином. Дадим их вывод.

Пусть имеются непрерывные функции Т]

(х, у, г) и (х, у, г), имеющие

ограниченные вторые производные во всех точках области т, заключенной

внутри поверхности а.

Рассмотрим тождество

(

дУ

\_дЦ

дУ

д*У[

дх \ 'дх у дх дх '

дх%

Проинтегрировав по переменной х, получим

Х\ XI Я1

Интегрируя по двум другим переменным, будем иметь

Уг г

7/2 г

г,

111 И о.^

XI г/1 21 У1 21 XI Ж1 1/1 21

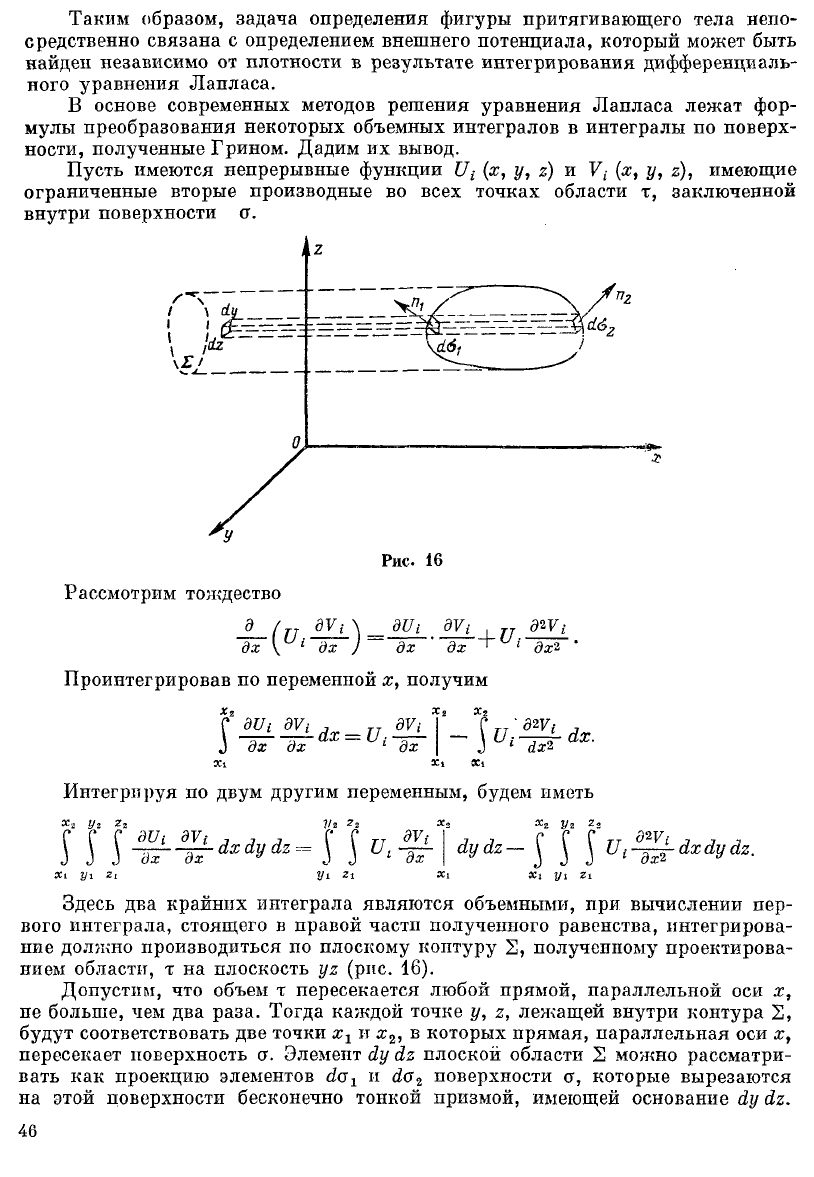
Здесь два крайних интеграла являются объемными, при вычислении пер-

вого интеграла, стоящего в правой части полученного равенства, интегрирова-

ние должно производиться по плоскому коптуру 2, полученному проектирова-

нием области, т на плоскость уг (рис. 16).

Допустим, что объем т пересекается любой прямой, параллельной оси х,

пе больше, чем два раза. Тогда каждой точке у, г, лежащей внутри контура 2,

будут соответствовать две точки х

и х

, в которых прямая, параллельная оси х,

пересекает поверхность а. Элемент йу

йг.

плоской области 2 можно рассматри-

вать как проекцию элементов йа

и йо

поверхности о, которые вырезаются

на этой поверхности бесконечно тонкой призмой, имеющей основание йу йг.

В этом случае йу йг = —Й0

соз (п

, ж) = йа>

соз (га

> Угол (га

, ж) —

>тйл между внешней нормалью п

к элементу (1а

и осью х всегда будет тупым,

а угол (п

, х) — всегда острым.

Используя полученные соотношения, можно интегрирование по контуру 2

=>?сти

к интегрированию по поверхности сг

У1 21

•

соз (п, х)йа.

VI 21

Таким образом,

тт

д2

У1

Напишем еще две аналогичные формулы, заменяя в них х на у и на г

и все три формулы сложим:

ас/г дУ{ , 91/; дУI , дцI

97/ •

ЗУ/

дх дх

д*У1

азV, , 927/

91/2

322

йт =

На основании (1.34)

ЛУ{ дУ

{

ду

ЗУ/

СОЗ

(п, у)-{--~С08(п, 2)

ЗУ/

^-соз(п,

ж)

+ соз (и, у) + -

-г-сов(п, г),

поэтому

дУг ЗУ/

дх дх

дХ]

ду

(

, ди

{

ду

ду ду

Зг Зг

йп

йо.

Обозначим

3[7/ ЗУ/ . 3^7/ ЗУ; , 9(7/ ЗУ/

дх дх ду ду Зг 9г

Из этого определения следует

так как перестановка функций и У,- сводится здесь к перестановке сомножи-

телей в трех слагаемых. При [/;= сонзЪ или У/= сопзЪ Б (?7/, У;) = 0. Также

очевидно, что

щи»

оба эти выражения представляют собой сумму квадратов первых производных

от и У,-.

Далее, сумму вторых производных от У

по х, у, г обозначим по-прежнему

через ДУ,-, так что

С)2 VI д*Ус д*У1 д.

дх* ' ду2 "Т" I-

Тогда первая или, как говорят иногда, предварительная формула Грина

будет иметь вид

х х а

Отметим, что в последнем интеграле производная берется по направлению

внешней нормали к поверхности о, восстановленной на элементе йсг.

Полученная формула Грина позволяет от объемных интегралов перейти

к интегралу по поверхности. Это очень важное обстоятельство, ибо в тех слу-

чаях, когда определить поведение тех или иных функций внутри тела мы не

можем, для нас очень важно уметь перейти от функций, заданных внутри тела,

к функциям, заданным на поверхности.

Положим теперь в (II.1) 17

= У,-, это дает

XX о

Второй интеграл слева имеет важное значение в теории потенциала; он

носит название интеграла Дирихле. Обозначим его через 1

йх.

Все элементы I, а следовательно, интеграл в целом, суть величины суще-

ственно положительные, / может быть равен нулю, в случае, если каждый

из его элементов обратится в нуль, но это возможно только при 17

{

= сопзЪ

во всех точках области т.

Таким образом, / ^ О, причем знак равенства относится только к случаю,

когда

171

= сонзЪ. Вследствие этого для всякой функции 17

имеет место не-

равенство

1 X

Положив в (11.1) 27,- = сопзЪ, найдем, сократив на 17

X а

Наконец, поменяем в (II.1) функции 17

{

и У,- местами, получим

+ ЩЪ-Цу^Аа. (П.5)

Т Т <у

Вычтем из (11.1) (II.5)

11 $ Ш~* = $ $ О(П.6)

т. о

Полученная формула называется второй формулой Грина.

Выведем теперь формулы Грина для функций II

и V

, непрерывных вне

поверхности сг, имеющих вне этой поверхности ограниченные вторые произ-

водные. Кроме того, для функций V

и У

ставится дополнительное (и обяза-

тельное) условие: они должны быть регулярны на бесконечности, т. е. удовлет-

ворять условиям (1.73), (1.74) и (1.75). Проведем радиусом В сферу 2 так, чтобы

поверхность а была бы целиком заключена внутри сферы 2 (рис. 17), и к об-

ласти т, ограниченной двумя поверхностями сг и 2, применим формулу (II.1)

х о 2

Элемент поверхности сферы й2 = В

зт 0Й0ЙА, и потому подынтегральное

выражение во втором интеграле правой части можно представить в виде

^е Ф- У=чд* 4тг

З1п

е ю ак,

йп ал

так как направление внешней нормали к поверхности 2 совпадает с направле-

нием радиуса сферы В. При В на основании свойства регулярности на

бесконечности, имеем

сШ

= сопз!, а Нт V'

Следовательно, при В, стремящемся к беско-

нечности, предел интеграла ^ равен ну-

лю. Поэтому

( И.7) Рис. 17

Отрицательный знак перед интегралом в правой части поставлен потому,

что за положительное направление нормали по-прежнему будем считать напра-

вление во внешнее пространство (внутрь т). Меняем Л

и У

местами

х а

Вычитая из (II.7) (II.8), получим

йп

йУ

•V.

йЦ

йп

Ло.

(".8)

(П.9)

Получим формулы Грина для функции

= 1/г, понимая под г расстояние

между текущей точкой М и данной точкой Р. В этом случае формула (11.6)

примет вид

йп

Для точки Р, лежащей вне объема т,

х о а

4 Заказ 1379

(П.Ю)