Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

гравиметрической съемки в области и Фаг — Ф

рав (2), получаемой мет

дом линейной интерполяции.

Вообще говоря можно было бы вычислить интерполированные уклонен!

отвеса вдоль звена триангуляции А В сколь угодно часто, а превышения кваг:

геоида между ними получить по формулам астрономического нивелированв,

(IX.42) и (IX.43). Однако, во-первых, при применении этого метода проис! •

дило бы значительное накопление ошибок, а во-вторых, потребовалась бы бо.~'

;

шая затрата труда на вычисления, ибо приходилось бы выбирать необходима

•

точки настолько часто, чтобы не оставалось сомнений в том, что уклоненг

отвеса между ними изменяются по линейное

закону.

I М. С. Молоденский разработал метод, п-

х зволяющий получить превышение квазигеои:

между точками, в которых известны астроном

геодезические уклонения отвеса без промеж;

точного интерполирования уклонений отвес

Разработанный им метод получил назваш'-

астрономо-гравиметрического нивелирование

У) В качестве исходных данных для оиределенп

превышения квазигеоида этим методом меж~

Рис

пунктами триангуляции А и В необходш:

иметь значения {А), г)

АГ

(А),

(В

Лаг (В) и гравиметрическую съемку некоторой области 2, внутри котг

рой находится данное звено триангуляции АВ.

Подставим значение составляющей Фдг уклонения отвеса (IX.35) в фот-

мулу (IX.42)

В В В

-(&•-&•)=$ о (2) <И+ + I [*(2') + Ав]<И. (1Х.4,

А А А

Первые два члена правой части соотношения (1Х.44) при наличии гравимет-

рической съемки в области 2 можно легко вычислить. Введем обозначен!?-

тогда

х> п

- № (2)- С

(2)] = У 0(2)Я + У (1Х.4Г

А А

-(&аг-?АГ) =-[^(2)-^

(2)] + У [Ф(2') + ДФ]йг. (IX.4»

Последний член формулы (1Х.46) вычисляют следующим образом. Спроек-

тируем астрономические пункты А и В на поверхность референц-эллипсоида.

принимаемую за плоскость. Введем прямоугольную систему координат с осью

совпадающей с направлением АВ, и началом координат в середине отрезка АВ.

Расстояние АВ обозначим через 21, а проекцию на референц-эллипеовд

текущей точки через Ь (рис. 58). В § 55 было показано, что при надлежаще**

выборе размеров зоны 2 можно добиться, чтобы функция, состоящая под ин-

тегралом в (IX.46), на отрезке АВ изменялась по линейному закону. Следова-

тельно, можно положить

Ф(2') +

АФ

Ьх.

(IX. 47

270'

В этом случае

В +1

| [д(2') + ДО]й2 = | (а + Ъх)0х = 2а1.

Для определения коэффициента а воспользуемся обстоятельством, что

в пунктах А и В значения суммы О (2') + ДО известны. Имеем:

в пункте А

х = —1, 0(2', Л) + М(Л) = 0

г(Л)-0(2, А) =

—

Ь1,

в пункте В

0(2', В) + АЪ(В) = Ъ

ат

(В)-Ъ(2, В) =

+ Ы.

Отсюда

_ ^аг^ + ^АГС-

) 0(3, Л)4-^(3, В)

~ 2 2

Следовательно,

[О

(2') +

ДО] й1

= [0

АГ

И) +

^АГ

(5)]

[О

(2, А) +

(2, В)} I.

После этого формула (IX.46) примет вид

- - = ^г

(Л)

+ 0

АГ

- (2) - & (2)] +

+ [0(2, Л)+ 0(2, Б)]/}. (IX.48)

Формула (1Х.48) для астрономо-гравиметрического нивелирования высот

квазигеоида была впервые получена М. С. Молоденским в 1937 г.

Выражение в фигурных скобках называется гравиметрической поправкой

в результат астрономического нивелирования, учитывающей нелинейность

изменения астрономо-геодезических уклонений отвеса между астрономическими

пунктами. Для вычисления этой поправки вполне достаточно одной лишь мест-

ной гравиметрической съемки в пределах области 2. Обычно границей этой

области принимают окружность некоторого радиуса В.

Формуле (IX.48) можно придать более простой вид

С2г - ^г = - ^аг

(Л)

+ ^АГ (*)]

+ ^ъ • (IX .49)

где

ЛЬ = Б

(2)-Е

(2)-*[0(2, Л) + ^(2, Я)]. (IX.50)

— гравиметрическая поправка.

Учитывая соотношение (IX.33), получим выражение для вычисления гра-

виметрической поправки

Д^ = ^(2)-^(2)-гШ

^4)

+1(2, В)] соз А +

[г]

(2, А) +

г]

(2, 5)] 81 п А). (IX.51)

Здесь I (2, А), I (2. Щ, Л (2> А) и г) (2, В) — гравиметрические уклоне-

ния отвеса в пунктах А и В, обусловленные влиянием аномалий силы тяжести

области 2; (2)

(2) — высоты квазигеоида в пунктах А

В, обусловлен-

ные влиянием той же области 2; 2 — область учитываемых аномалий, радиус

которой принимается равным В^

(В — радиус Земли, г)5

— угловое расстоя-

ние от астрономического пункта до границы области), который должен быть

в полтора — два раза больше расстояния (2/) между астропунктами.

271'

Значения высот квазигеоида и гравиметрических уклонений отвеса, ос

условленных влиянием аномалий круговой области 2, обычно вычисли?

по формулам Стокса (VIII.53) и Венинг-Мейнеса (VIII.59)

•фо 2Я

И (1Х.51

о о

1|>о 2Л

= (IX.5*

о о

1|>о 2Л

^""ггИ (IX.5^

о о

В условиях равнинной) района (когда к = ЮЦ < 0,01) можно польз':

ваться формулами Стокса и Венинг-Мейнеса для плоскости, которые опреде-

ляются из соответствующих формул для сферы (VII 1.57) и (IX.52) при В

-*•

ос.

Обозначив через г — линейное расстояние от исследуемой точки до текущей

и учитывая, что

, Ас

Я _]н->-со Г

ИтГ ^ 1 = - —

иш

1_ п*

получим

6(2) = —^-0-^оовАЛт, (1Х.56-

Превышения квазигеоида могут быть получены двумя способами.

Первый способ, получивший широкое применение до 1969 г., состоит

в непосредственном вычислении величины Д^ по аномалиям силы тяжести,

без вычисления высот квазигеоида и уклонений отвеса в пунктах А и В.

Гравиметрической поправке можно придать вид

ЛЬ-^ИС*-?)^)**,

(2)

где в соответствии с обозначениями рис. 58.

В А I-

А ^

Для вычисления величины М. С. Молоденский предложил использо-

вать новую систему координат — софокусных эллипсов и гипербол с фокусами

272'

в точках А

В, координатные линии в которой образуют ортогональную систему;

положение текущей точки характеризуется значениями а и

полуосей эллипса

н гиперболы, проходящих через эту точку.

Гравиметрическая поправка в этой системе примет вид [9]

= Ь)8с8с1,

(2)

где 11 2

(

{(а-ь^ (а + 6)3 | аЬ

Интеграл по площади 2 вычисляют методами численного интегрирования-

Затруднение возникает лишь для двух точек — фокусов координатных линий А

и В, где М обращается в бесконечность.

Однако это затруднение отпадает, если на площади околофокальных сек-

торов аномалию силы тяжести выразить через горизонтальные градиенты.

Рабочую формулу для вычисления превышений квазигеоида (первым

способом) получим, разделив обе части равенства (1Х.49) на 2/зш 1":

1шпЬ — Т {Л) + *лг (5)1" + ^г. (IX.58)

Левая часть полученного выражения представляет собой средний наклон

квазигеоида относительно референц-эллипсоида на участке АВ, выраженный

в секундах дуги.

В настоящее время принят способ вычисления превышений квазигеоида,

основанный на раздельном вычислении каждого из членов, входящих в (IX.50),

по гравиметрическим данным. Такой способ, предложенный О. М. Остачем,

оказался наиболее целесообразным при использовании ЭВМ, он значительно

сокращает объем вычислений и дает более реальную оценку точности астроно-

мо-гравиметрического нивелирования. Применение этого способа не требует,

чтобы область интегрирования при вычислении I, (2) и О (2) для пунктов А

п В была одинаковой, что необходимо при вычислении гравиметрической по-

правки другими методами. В этом случае вместо I, (2), вычисляемой по

формуле (IX.52), следует вычислять Д^ (2) по формуле

•Фо 2Я

41Л ^ (е-тНЯДО-Я^оИвтфАМ,

о о

где 8 (ф

) — значение функции Стокса при <р = г|)

. Радиус зоны интегриро-

вания я|э

принимается равным примерно 2—3°.

Формулу (1Х.49) удобнее представить в виде

^АГ

- = - №

}

АГ (А)-Ъ (2, А)] + [0

АГ

(В)

-0(2, Я)]}г + Д^(2)-Д^(2). (IX.59)

Рабочая формула для вычисления высот квазигеоида (в метрах) имеет вид

?аг ~ ^аг = -0.00449 [(ДЕ

+ ДЫ ДЯ + (АЛа + АЛВ) соз В

ДЦ +

+ Д^(2)-Д^(2), (IX. 60)

18 Заказ 1379

273;

где А В = В

— В

, АЬ = Ь

— ЬА — соответственно разности широт и дол-

гот пунктов, выраженные в минутах дуги; В

= 1/2 (В

+ В

) — средняя

широта пунктов; А%,А, ААт]а, АУ]В — разности слагающих астрономо-гео-

дезических и гравиметрических уклонений отвеса в меридиане и в первом вер-

тикале для астропунктов А и В.

§ 57. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ОБЛАСТИ

ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ, НЕОБХОДИМОЙ

ДЛЯ АСТРОНОМО-ГРАВИМЕТРИЧЕСКОГО НИВЕЛИРОВАНИЯ

Определение области 2 — основной вопрос, возникающий при астроно-

яо-гравиметрическом нивелировании. При решении задачи М. С. Молоденский

исходил из условия, чтобы влияние аномалий в той части поверхности Земли

2', по которой интегрирование не производится, на величину гравиметриче-

ской поправки было бы менее задаваемой точности астрономо-гравиметриче-

ского нивелирования. При этом М. С. Молоденский не учитывал погрешности,

обусловленные нелинейностью изменения угла АФ.

Область 2 учитываемых аномалий рассматривается как круг радиуса В

с центром в начале координат.

Поскольку

0(2) = -^.

выражение для гравиметрической поправки имеет вид

А^з = (2) - (2) -1 .

Гравиметрическая поправка, обусловленная влиянием неучитываемых

аномалий области 2', определяется аналогично

А^г» = (2') - (2')

•-1

+ • (IX.61)

Величина А^' является той остаточной ошибкой, которая обусловлена

всеми неучитываемыми аномалиями области 2'.

Следовательно, задача состоит в определении радиуса области 2, по кото-

рой производится интегрирование, таким образом, чтобы величина Абыла

в допустимых пределах.

Поскольку линия АВ целиком расположена в области 2, каждый из членов

правой части (IX.61) можно представить в виде ряда:

ь —

НзГ—да—+з"! Лз—^

ТА (У\ ТО 1У'\ 1 [

12 13

) ь ) —

Н-Т! Ш 51 Ш 1-

•

2! ОЯ 3! 01%

, _ гс°(3') [ ,«а

е°(Д') |

01 01 "I дП "Г'2! 013

1 д$

(Г) , 01? (Г) I»

01 01 012 "г" 2! д1*

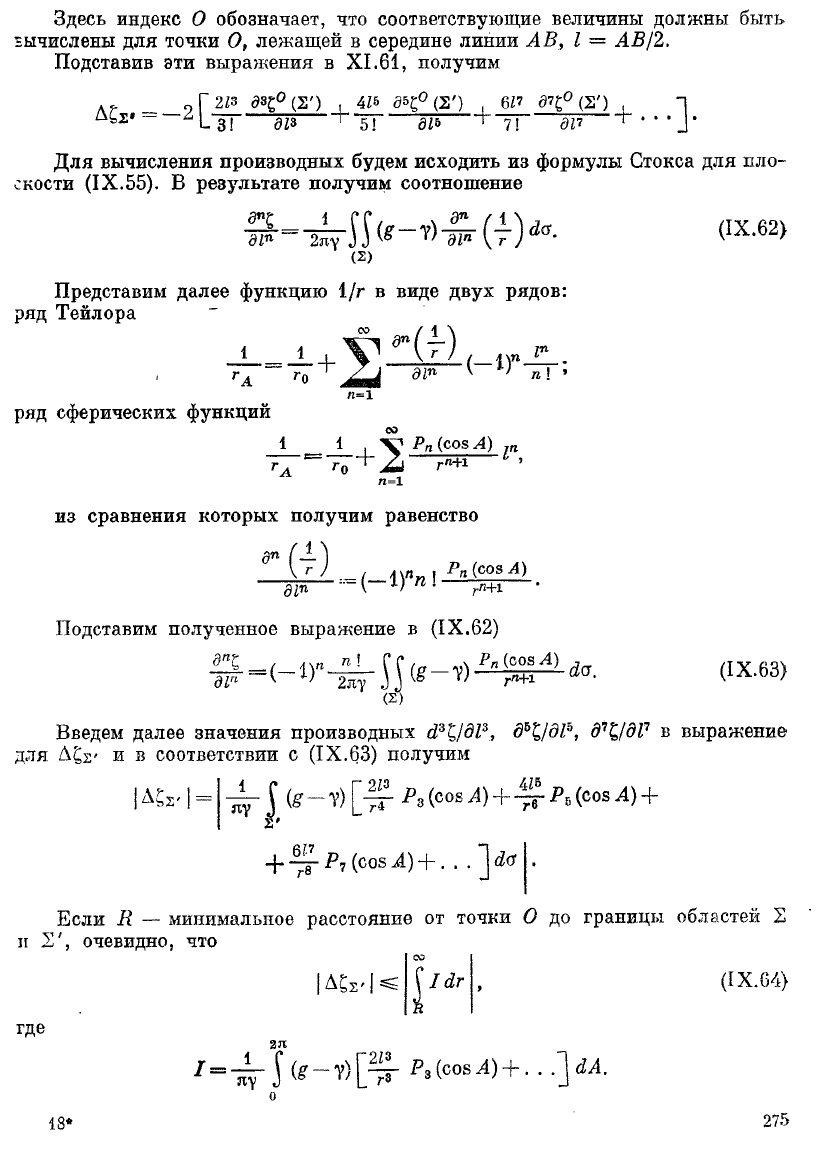
Здесь индекс О обозначает, что соответствующие величины должны быть

вычислены для точки О, лежащей в середине линии АВ, I — АВ/2.

Подставив эти выражения в Х1.61, получим

кг _ оГзгз азс°(Г) , ы* дь^(ц') , ег? , 1

Щз ^-51 он Ш г •••_]•

Для вычисления производных будем исходить из формулы Стокса для пло-

скости (IX.55). В результате получим соотношение

З-^-Яс-!»^)*- <

1Х

(2)

Представим далее функцию 1 /г в виде двух рядов:

ряд Тейлора

'(г)

+ ^

Я1П ( п I '

д1п л!

ряд сферических функций

1 1 , Р„(созЛ)

г"+1 ''

п=1

из сравнения которых получим равенство

в»

/ _ / лчп„

-Р«(созЛ)

_ (—а; п .

Подставим полученное выражение в (IX.62)

(2")

а*» -(-«"-Й-И^-^-

(1Х

63)

Введем далее значения производных д

Уд1

, д^/дР в выражение

для и в соответствии с (IX.63) получим

[

От - у) [тг (соз

Л)

+ Р

(СОЗ

4) +

Если Я — минимальное расстояние от точки О до границы областей Б

и 2', очевидно, что

/А-

где

2Я

=1 <*'-

^3 (соз л) + . . .] а А.

(IX. 64)

17* 275

Поскольку модуль суммы меньше или равен сумме модулей

2Э1

Применим к каждому члену последнего выражения неравенство Шварг

ф1|5 йсг

"^ф

ЙСТ

Го|5

.2 2

йа

где ф и гр — две функции действительного переменного, заданные в области

На основании неравенства Шварца

|яу/|<

2Л -|«/«

Г2Л

Р${созА)с1А

о -I 1-о

• 4/5

~Г

'2Я

Обозначим

!-0

(IX,-

2Л

Очевидно, что это есть среднеинтегральное значение величины — у,

на окружности некоторого радиуса г. Таким образом,

2Я

§ (2-А =2я(е-у)1.

Поскольку

РI (соз А) = ("I соз

А -1

соз

А)

= ^-С08

А-^- соз

А + соз

А,

то

2Л

Подставим всюду в (IX.65) Р| (соз 4) вместо Р\ (соз А), Р* (соз А), .

•

имея в виду, что

2 Л 2Я 2 Л

получим

или

| Р1 (соз А) а А > | (соз Л) > ^ Р

(соз А)д,А>

о о

3 I

—Т)т I 223 415

V ,

276'

Неравенство (IX.64) в результате примет вид

В этом неравенстве под (^ — у)

следует понимать среднее квадратическое

значение аномалии на окружности радиуса В (с центром в О), а не максималь-

ное ее значение в области 2' по той причине, что интеграл убывает чрезвычайно

быстро и его величина определяется почти исключительно аномалиями вблизи

нижнего предела, т. е. вблизи границы областей 2

2'-

После интегрирования по г и подстановки пределов получим

Поскольку сумма членов бесконечно убывающей прогрессии равна

ц.

да—га '

разделив числитель и знаменатель дроби на I

и обозначив

получим

Д2 —22

2_1 •

Неравенство (IX.66), таким образом, принимает вид

1А

17 (8 — у)т.

•

р2 —1

Разделив обе части этого неравенства на величину 21 и выразив — у)

в миллигалах, а угловые величины в секундах дуги, получим

ет-И'

'^ <

1х

Формула (IX.67) служит для подсчета случайной части ошибки гравимет-

рической поправки для отдельного звена, обусловленной ограничением области

интегрирования расстоянием В = I р от середины звена.

При 21 = 70 км, р = 3, В = 105 км, и (§ — у)

== 15 мгл

Л&Х'

21 8111 1"

<0,2",

что соответствует ошибке в превышении квазигеоида порядка 0,1 м. Такая

точность определения превышений является для практических целей вполне

достаточной.

В конкретных условиях значения величины (§ — у)

на контуре 2 берут

с гравиметрической карты. Соответствующая предельная ошибка, определя-

емая формулой (IX.67), в равнинных районах близка к ±0,2 — ±0,3". Расчеты

показывают, что в равнинных районах вполне можно вместо р = 3 принять

р = 2.

277'

Последнее утверждение можно доказать, рассчитав верхний предел накопле-

ния систематических ошибок в гравиметрических поправках при астрономо-гра-

виметрическом нивелировании.

М. С. Молоденский дает формулу для определения верхнего предела на-

копления систематических ошибок в превышениях квазигеоида на конце ходо-

вой линии нивелирования за счет ограничения области интегрирования

на каждом звене радиусом Е = р1

Из приведенного примера видно, что даже при значении р = 2 не проис-

ходит чрезвычайного накопления ошибок.

Отсюда можно сделать вывод, что при выполнении астрономо-гравиметри-

ческого нивелирования аномалии силы тяжести достаточно знать в полосе ши-

риной от 41 до 6/.

Увеличение ширины полосы не дает существенного повышения точности;

гораздо важнее увеличение плотности гравиметрических пунктов вокруг

каждого из астропунктов.

Рассмотрим влияние ошибок на результаты астрономо-гравиметрического

нивелирования и меры, обеспечивающие получение результатов с требуемой

точностью.

Поскольку при астрономо-гравиметрическом нивелировании астрономо-гео-

дезические данные используются совместно с результатами гравиметрической

съемки, конечные результаты нивелирования будут зависеть от ошибок опре-

деления геодезических, астрономических координат и ошибок гравиметриче-

ской съемки.

Для оценки влияния различных ошибок на вывод превышений квазигеоида

над принятым референц-эллипсоидом будем исходить из формулы (IX.48),

которую перепишем в виде

Основная часть ошибки, накапливающаяся от звена к звену, определяется

первыми двумя членами. Поэтому при ориентировочном подсчете суммарных

ошибок третьим членом можно пренебречь и, кроме того, вместо величин укло-

нений отвеса, вычисленных отдельно для точек А и В, можно принять средние

величины для данного звена. Полагая

(IX.68)

При (§• — у) = 50 мгл, I = 100 км, и р = 2 получим

!8^|<0,5 м.

§ 58. ИСТОЧНИКИ ОШИБОК

АСТРОНОМО-ГРАВИМЕТРИЧЕСКОГО НИВЕЛИРОВАНИЯ

И ПУТИ ОСЛАБЛЕНИЯ ИХ ВЛИЯНИЯ

получим

0(2, А) = 0(2,

АСаг=-2/0

Г + 2№

278'

Таким образом, ошибка определения превышения квазигеоида включает

ошибки геодезических, астрономических и гравиметрических измерений.

Если влияние ошибок геодезических измерений на величину ошибки опре-

деления превышения квазигеоида определять отдельно, то ошибка определе-

ния превышения квазигеоида, обусловленная только погрешностями астроно-

мических определений широт и долгот и погрешностями гравиметрических

данных будет так называемой «ошибкой собственно астрономо-гравиметриче-

ского нивелирования».

Обозначив через т$

среднее квадратическое влияние ошибок астрономи-

ческих определений на астрономо-геодезическое уклонение отвеса, а через

— среднюю квадратическую ошибку гравиметрического уклонения отвеса,

получим для отдельного звена

= -^-21, (IX.69)

^ = (IX.70)

где р" = 206265".

Ошибка определения превышения квазигеоида на отдельном звене триан-

гуляции при расстоянии между астрономическими пунктами, равном 21, опре-

деляется по формуле

™<1=%гУт1

+ т1

. (1Х.71)

Обозначив

ГПъ

получим

т^-^-21. (IX.72)

Ошибка передачи превышений квазигеоида вдоль линии нивелирования

длиной Ь в случае звеньев с равной длиной будет вычисляться по формуле

т*

^21 Уп УШ, (IX.73)

Р" ' р"

где п = Ь/21.

В этом случае ошибка определения приращения высоты квазигеоида опре-

деляется по формуле, предложенной Л. П. Пеллиненом,

т.

•уц

"Г-7-1/Т2 М С08 Р,-, ,

1, (IX.74)

где яI — длина г-й стороны нивелирования; р,-, ,-

— угол между I и I + 1

сторонами.

Формулу (IX.73) обычно представляют в виде

;

=ц

УТ, (IX. 75)

где р,; — ошибка на 1 км хода нивелирования, равная

^(юо-^/й) см. (IX.76)

279'