Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Если в < к, то метод Аронова — Бьерхаммара выгодно применять липп

для выделения регионального влияния. При этом понадобится меньше при-

ближений, если в качестве исходных аномалий принять не точечные, а средние

аномалии по квадратам размером й X й (расстояние д, больше расстояния

и отвечает условию й^>к).

После выделения регионального влияния вычисления должны выполняться

в поле остаточных аномалий. Чтобы использовать электронную машину, вы-

годно задать аномалии и соответствующие им высоты в узлах более густой

квадратной сетки, стороны которой меньше среднего расстояния между грави-

метрическими пунктами.

§ 51. ИСПОЛЬЗОВАНИЕ «ЧИСТЫХ» АНОМАЛИЙ

В настоящее время спутниковые методы позволяют определять высоть.

квазигеоида с ошибкой порядка нескольких метров. Таким образом появляется

возможность вычислять чистые аномалии силы тяжести.

Связь между чистой и смешанной аномалией на основании (VIII.4) уста-

навливается в виде

(ём ~

Ум)

= (ём -

Ум)

- (-^г)

или

(ем — Ум )мгл = (ём — Ум)мг

— 0,30862;

Переходя к средним квадратическим ошибкам, получим

Ьм~Ум) =

»(«м-Т№) +

095т

Принимая ошибку т% определения высоты квазигеоида по спутниковым

данным порядка 10 м, получим

Ьм~Ум)

= т

Ьм~Ун) + (

Следовательно, чистая аномалия получается несколько грубее смешанной,

однако при учете влияния дальних зон в областях разреженной гравиметри-

ческой съемки, где приходится прибегать к интерполированию аномалий,

применение чистых аномалий вместо смешанных дает определенные преиму-

щества. Имея в виду, что расчеты, связанные с использованием чистых ано-

малий, носят приближенный характер, дадим вывод формул для возмущающег'

потенциала и составляющих уклонений отвеса в стоксовом приближении.

Граничное условие для возмущающего потенциала в точках физической

поверхности Земли дается формулой (VIII.2). Отнесем это условие к поверх-

ности сг сферы радиуса В

дт . .

(ём Тм).

др

[Г+В

Задача определения возмущающего потенциала в такой постановке сво-

дится к внешней сферической задаче Неймана. Для ее решения воспользуемся

интегралом Пуассона (11.41) и применим его к функции р (дТ/др) (эта функция,

так же как и Т, будет гармонической на основании леммы, приведенной в § 12:

Будем иметь

(

дт

СГ ~ ЭТ р

—Л

, с

240'

Но на поверхности а сферы р = Е, дТ/др = —— Ум), поэтому

ии. так как при интегрировании по сфере р будет величиной постоянной

Интегрируя это выражение по р, в пределах от р до оо

и замечая, что*

Т — 0, получим

ргз

со

гр

рг»

л 2

Из соотношения (11.37) легко получить формулу, аналогичную (11.44)

ргЗ

гр ^ др V г )'

Таким образом,

Поскольку

г'Лучаем

1 , №

—

Дрс051|)+

Иг

Л р

Но при р оо, г

-*•

оо, Нш = 1, и потому

—

ДрсоягЬЧ-йг ..

11П1 * - =Е(1 — С08

'Следовательно,

О рг»

г н рп (1 — 0081)3)

оо

Окончательно получим

г. ^ - V,,) [4 - -1гг;

Эта формула дает возможность вычислить возмущающий потенциал во-

».-г:;шем пространстве по заданным чистым аномалиям на сфере. Можно вос-

а- --.ьзоваться ею для вычисления Т на поверхности о сферы; в этом случае-

слглует положить р = Е, г = 2Е зт-^-'

I'-' 3»иая 1379 244

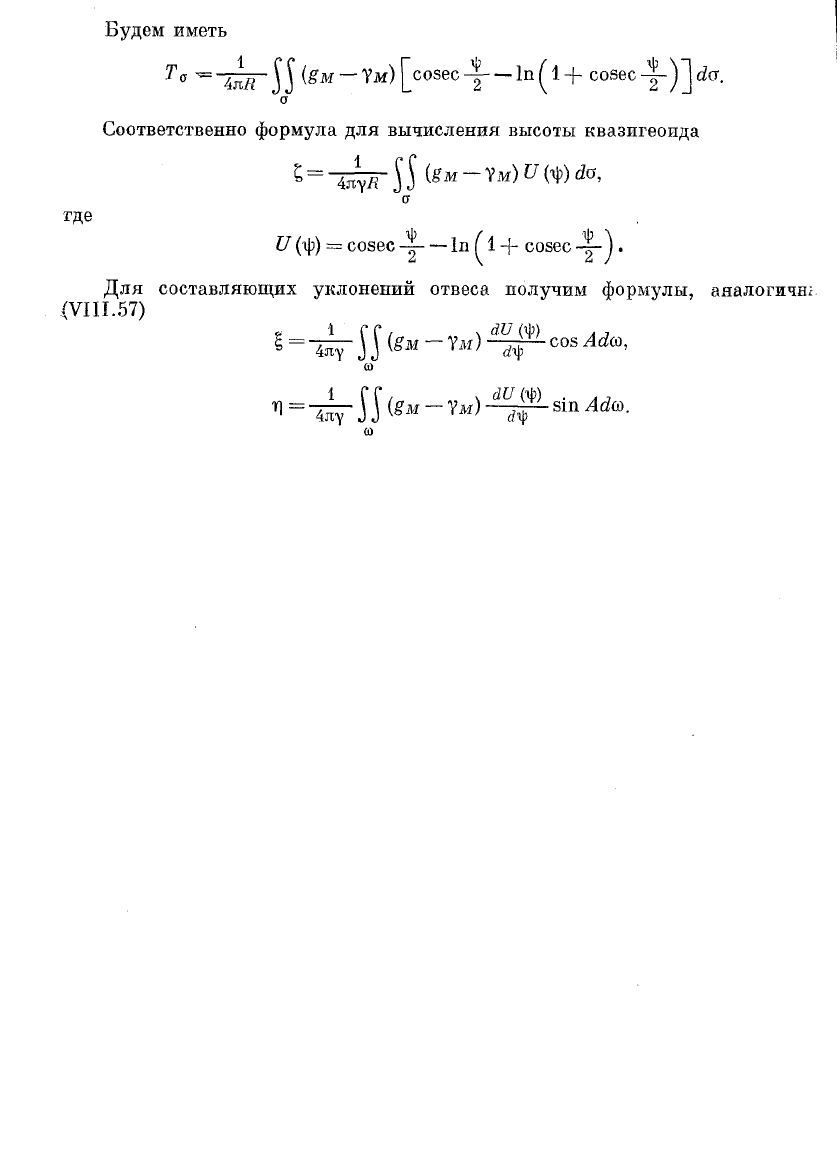
Будем иметь

Та — [созес— 1п(Ч+ собес

Соответственно формула для вычисления высоты квазигеоида

где

II (яр)

= созес

1п ^ 1

+ созес

Для составляющих уклонений отвеса получим формулы, аналогична

/VIII. 57)

1 =

{ём

Ум) 008 М(

^ =

Ум)

81п

Глава IX

ИСПОЛЬЗОВАНИЕ МЕСТНОЙ ГРАВИМЕТРИЧЕСКОЙ

СЪЕМКИ В ГЕОДЕЗИИ

§ 52. НАЗНАЧЕНИЕ МЕСТНОЙ ГРАВИМЕТРИЧЕСКОМ СЪЕМКИ

В предыдущей главе были подробно рассмотрены способы определения

возмущающего потенциала Земли Т, а также величин | и т] в произвольных

точках земной поверхности.

Выведенные в этой главе формулы дают возможность вычислить геодези-

ческие координаты В, Ь и Н точек земной поверхности относительно принятого

общего земного эллипсоида, т. е. в конечном счете определить фигуру Земли

в целом.

Важной отличительной особенностью полученных в предыдущей главе

формул является необходимость интегрирования аномалий силы тяжести по

всей поверхности Земли.

В настоящее время при обработке геодезических измерений и решения

практических задач геодезии в пределах одного или нескольких государств,

расположенных на одном континенте, в качестве координатной поверхности

принимают поверхность референц-эллипсоида.

Референц-эллипсоидом называется эллипсоид определенных размеров,

ориентированный в теле Земли так, что геодезические координаты какого-либо

одного пункта поверхности Земли (выбираемого в качестве исходного) при-

нимаются равными некоторым заданным величинам.

Можно, например, положить, что геодезические координаты В

и Ь

исход-

ного пункта в точности равны астрономическим ср

и к

. Однако практически

оказывается, что геодезические координаты: широта В

, долгота Ь

, азимут А

и высота Н

исходного пункта несколько отличаются от астрономических <р

, а

и нормальной высоты Щ на некоторые малые величины (Б

— ср

(Ь

— Я

), (А

— а

) и (Н

— Щ). В этом случае возникает задача их точного

определения.

Задача подбора геодезических координат В

, Ь

, А

и Н

, в исходном

пункте триангуляции, а также сжатия а и большой полуоси а референц-эллип-

соида называется установлением исходных геодезических дат. Она может быть

решена различными методами, подробно рассматриваемыми в курсе высшей

геодезии.

Поскольку геодезические координаты в исходном пункте земной поверх-

ности считаются известными, задача определения геодезических координат

относительно референц-эллипсоида в других пунктах фактически сводится

к определению лишь приращений координат.

16* 243-

Для определения приращений геодезических координат вся территорг

подлежащая изучению, покрывается триангуляционными, трилатерационнк«

или полигонометрическими сетями, а также нивелирными полигонами.

Геодезические координаты любого пункта, соединенного с исходна

в системе референц-эллипсоида, вычисляют по формулам

В = В

+ АВ \

1 = Ь

+ АЬ ,

Я = Я

+ДЯ

АГ

]

где В

, Ь

, Я

— геодезические координаты исходного пункта триангулянг"

А В и А Ь — приращения широты и долготы, получаемые в результате решег

прямой геодезической задачи на эллипсоиде; АЯаг — приращение геоде

ческой высоты над референц-эллипсоидом

Геодезическая высота Я имеет двоякое значение: во-первых, является одб

из пространственных координат и потому должна определяться не менее точно, ч

другие координаты, во-вторых, необходима для получения плановых коордпг

методом проектирования. Приращение геодезической высоты АЯ

г может б;

получено без использования результатов гравиметрической съемки нето~

тригонометрического нивелирования. Например, формула М. С. Молоденск

позволяет вычислять АЯдг

используя измеренные зенитные расстояния

А#аг = -у- (соз2!.2 — соз2

+ (/У

—А^ + АЯ

АГ

) зш

-|-,

где 5 — расстояние между точками 1

2; г

— зенитное расстояние направо

ния из первой точки на вторую; г

ал

— обратное зенитное расстояние; .

и N2 — радиусы кривизны первого вертикала эллипсоида в точках 1 и 2; V

угол между координатными линиями Н

и Н

Однако необходимо учитывать, что на точность измеренных зенитш

расстояний большое влияние оказывает вертикальная рефракция. Вследст;

этого метод тригонометрического нивелирования при высокоточном опред(."

нии геодезических высот не применяется.

Для точного определения приращений Д#аг приходится раздельно оп;

делять приращения нормальных высот АН

и высот квазигеоида Д^

дг

от:

сительно референц-эллипсоида, после чего из соотношения

АЯ

АГ

==ДЛ

+ АСАГ, (IX.

полученного из (VI.22), находят АЯдг- Д

ЛЯ

вычисления приращений А.

и А^аг требуется местная (региональная) гравиметрическая съемка, выполг

емая в определенной ограниченной области.

Прежде чем определять приращения геодезических координат А В и

методами сфероидической геодезии, необходимо линейные и угловые измеренг

производимые на физической поверхности Земли, редуцировать на пове[

ность референц-эллипсоида. Для этого требуется знать так называемое аст;

номо-геодезическое уклонение отвеса и и геодезическую высоту Я над пове;

ностью референц-эллипсоида. Астрономо-геодезическим уклонением отв1

называется угол (п, §) (см. рис. 34) в точке наблюдения, образованный отвесн

Здось и далее все величины, вычисляемые относительно референц-эллипсоида СУ

жены подстрочным индексом — АГ, означающим астрономо-геодезическую величину.

244'

шией и нормалью к поверхности референц-эллипсоида. Составляющие этого

•да в плоскостях меридиана и первого вертикала получают по разностям

трономических и геодезических координат

| Угол (у, §) (см. рис. 34) в дальнейшем будем называть гравиметрическим

уклонением отвеса, поскольку он определяется через аномалии силы тяжести.

Как видно из сопоставления выражений (VI.5) и (IX.2), составляющая 1аг

•строномо-геодезического уклонения отвеса в плоскости меридиана отличается

•т составляющей % гравиметрического уклонения отвеса в той же плоскости

ва величину поправки А В — поправки за кривизну силовой линии нормальной

сшлы тяжести

Что касается возможности вычисления составляющих уклонений отвеса |аг

• Чаг по формуле (IX.2), то следует иметь в виду, что астрономические коорди-

•аты ф и X могут определяться не на каждом пункте триангуляции. При по-

строении государственной геодезической сети в СССР предусмотрено размеще-

пе на обоих концах выходных сторон триангуляции 1 класса, находящихся

шл расстоянии 200—250 км друг от друга, так называемых пунктов Лапласа,

• которых определяются ср, X и а, а в середине звеньев (примерно через 70—

1100 км) — промежуточных астрономических пунктов, в которых определяются

лшшь ф и X. Поэтому составляющие уклонений отвеса могут быть вычислены

шо формуле (IX.2) только в тех пунктах триангуляции, где измерены астроно-

мические широты и долготы. Во всех остальных пунктах составляющие укло-

нений отвеса получают путем интерполирования с использованием гравиметри-

ческих уклонений отвеса.

Таким же путем можно получить геодезические координаты пунктов, на

которых выполнены одни лишь астрономические определения.

Следовательно, местная гравиметрическая съемка используется для реше-

кая следующих задач:

1) получения поправок в измеренные превышения при вычислении раз-

«остей нормальных высот АН

;

• 2) определения приращений высот квазигеоида А^

лг

;

3) вычисления интерполированных уклонений отвеса в пунктах триангу-

дяппп;

| 4) получения геодезических координат астрономических пунктов, не явля-

Задача точного определения высот пунктов, расположенных на физической

•оверхности Земли над принятым референц-эллипсоидом, достаточно сложна.

Высоты вследствие сложной формы земной поверхности подвержены резким

|колебаниям и не могут быть получены непосредственно из измерений. Обычно

|кх принято делить на две части: наиболее резко меняющуюся (так называемую

пшсометрическую), отражающую всю сложность физической поверхности

При условии, если за уровенный эллипсоид принят референц-эллипсоид. В против-

аом случае должна быть учтена поправка за несовпадение нормалей к уровенному эллип-

свкху и к референц-эллипсоиду.

(1Х.2)

юшпхся пунктами триангуляции.

§ 53. СИСТЕМЫ ВЫСОТ

245'

Земли, и более спокойную, меняющуюся плавно на довольно значителы-

расстояниях. Назовем ее условно геоидальной частью.

Выделение из геодезической высоты гипсометрической части имеет ва;г ^

значение и вызвано многовековой практикой человечества, связанной с ре;:

нием различных практических задач. Гипсометрическая часть геодезичес:- -

высоты получила название высоты над уровнем моря. Геоидальную ча,:

высоты можно рассматривать как высоту уровня моря над поверхностью ре

ренц-эллипсоида.

Рассмотрим способы определения гипсометрической части высоты. По*.

жем, что гипсометрическая часть высоты не может быть получена лишь в резул.

тате чисто геометрического процесса нивелирования.

Поверхность Земди

Получаемая в процессе нивелирования разность отсчетов к.

— к

= ^

по рейкам называется измеренным превышением. Это превышение равно отрез?

отвесной линии между уровенными поверхностями, которые пересекают физ;

ческую поверхность Земли в точках стояния нивелирных реек.

При выполнении нивелирования между значительно удаленными др;

от друга точками возникает необходимость вставлять промежуточные точь

и нивелировать линию по частям. В результате суммирования нивелирнк

превышений вдоль линии нивелирования от уровня моря (начальной точк:

до определяемой точки В получается измеренная высота (рис. 53)

изм

= 2дл.

Если считать перемещения вдоль линии нивелирования и сами величины

бесконечно малыми, то

Измеренные превышения А к (йк) в разных местах между одними и теми ^

уровенными поверхностями будут различными вследствие непараллельное:,

уровенных поверхностей и потому измеренная высота, получаемая как сумм

измеренных превышений, зависит от направления ходовой линии.

246'

В этом легко убедиться. Положим, что нивелирование совершается по

двум направлениям (см. рис. 53): 1) от уровня моря (точка О) до точки И, затем

вдоль уровенной поверхности до точки В и 2) от точки О вдоль уровня моря

до точки С, а затем до точки В. В первом случае 2 &к=00, а во втором —

олв

2 Ай = СВ, т. е. измеренная высота точки, полученная по ходам ОВВ

осв

и ОСВ, имеет неодинаковое значение. Следовательно, поскольку измеренные

таким образом высоты не определяются однозначно, они непригодны для прак-

тического использования в геодезии.

Для определения гипсометрической части высоты рассмотрим две системы

высот: нормальную Н

и ортометрическую Н

Разумеется, что любая система определения гипсометрической части высоты

должна быть связана с задачей определения высот точек земной поверхности

над принятым эллипсоидом, для чего необходимо решить вопрос о соответ-

ствующем определении другой части геодезической высоты — геоидальной.

Система нормальных высот, введенная в СССР по предложению М. С. Мо-

лоденского, полностью соответствует теории определения фигуры Земли и за-

даче определения геодезических высот точек земной поверхности.

При разложении возмущающего потенциала в ряд Тейлора (§ 31) был

дЮ (В, О) „у „

опущен член ^ — Н

-АВ. Подсчитаем его значение.

Поскольку

дЦ(В, О)

-V.

дЮ'

то, используя (У.41), получим

дт(В, О) ду о • о

дНУдВ

~дВ

= 81П ф

а приняв зш 2ф = 1, р Узос» А В = 0,6'

д2П 0)

АВ = 10~

• V» •

<)НУдВ

Уе

Поскольку далее аномалия высоты ^ получается делением возмущающего

потенциала Т на значение нормальной силы тяжести у, то погрешность высоты,

обусловленная членом

дууд^ Н

АВ, будет порядка (Ю

-6

)/у ^ 10~

Таким образом, сумма высоты квазигеоида и нормальной высоты опре-

деляет высоту точки над отсчетной поверхностью даже при Н

= 10 км с ошиб-

кой менее 1 см, а при ВТ* = 1 км — с ошибкой менее 1 мм.

Следовательно, даже в первом приближении задача определения геодези-

ческих высот решается в теории М. С. Молоденского с точностью, вполне удо-

влетворяющей решение практических задач.

Ортометрической высотой называется расстояние между точкой физической

поверхности Земли и поверхностью геоида, отсчитываемое по отвесной линии,

проходящей через рассматриваемую точку. На рис. 53 отрезок СВ отвесной

линии — ортометрическая высота точки В.

Ортометрическая высота может быть получена через разность потенциалов

точек В и О. Поскольку точки О я С лежат на одной и той же уровенной поверх-

ности

247'

Считая, что на отрезке С В известно среднее значение силы тяжести

заменим переменное значение § ее средним значением, т. е. положим

лл х>

[

йк = е»\Ак.

Сумма элементарных превышений от С до В, очевидно, равна отрезку СБ.

т. е. ортометрической высоте точки В, которую обозначим И%. Таким образо«_

ёт^в = | Л

отсюда

ТТ& б

В = 5 = 5 . (IX.

8т 8т

Из (IX.3) видно, что ортометрические высоты определяются однозначн.

поскольку разность потенциалов между точками физической поверхности

Земли О и В не зависит от направления нивелирного хода.

В соответствии с ортометрической высотой должна быть определена и вто-

рая составляющая геодезической высоты, т. е. ее геоидальная часть.

В данном случае геоидальной частью высоты является отрезок В

С (см.

рис. 53), который называют высотой геоида над эллипсоидом (обозначим ег'

через П-

Если бы значение возмущающего потенциала в точке геоида С было бь

точно известно то величина % определялась бы согласно (VI.

19)

аналогично*

формулой

Г'-

с I Цр-Ко

V V '

где Тс — значение возмущающего потенциала в точке геоида С. Однако опре-

делить потенциал внутри притягивающих масс, не зная с достаточной точность:-

их плотность, не представляется возможным.

В свою очередь оказывается, что нельзя вычислить точное значение орто-

метрической высоты по формуле (IX.3) из-за невозможности точного определе-

ния величины

Остановимся на этом вопросе несколько подробнее. В принципе вели-

чина д

может быть найдена либо из наблюдений, либо — в результате вы-

числений.

Для того чтобы использовать первый путь, необходимо вдоль линии ВС

пробурить скважину и измерить силу тяжести на различных глубинах вплоть

до поверхности геоида. Тогда может быть выведена как среднее значени»

из всех измеренных величин. Очевидно, такой способ определения § нереален.

Другой метод определения §

состоит в вычислении значения §

с использо-

ванием редукции Прея. Этот метод был разработан швейцарским геодезистом

Нитхаммером в 1932 г.

Редукция Прея дает возможность получить действительное значение силы

тяжести внутри притягивающих масс, в данном случае в точке Б (средней

точке ортометрической высоты) (см. рис. 53).

Достигнуто это может быть следующим образом.

218'

Из измеренного значения силы тяжести в точке В — дв вычитается вли-

ввне внешних притягивающих масс, лежащих между точкой наблюдений В

• точкой Б. Точное значение этого влияния должно быть вычислено по формуле

1*11.3)

пе б — плотность в текущей точке внутри притягивающих масс и интегриро-

вание распространяется на всю учитываемую область. После введения этой

«оправки будет получено значение силы тяжести в точке В, которое было бы

жри отсутствии внешних притягивающих масс. Далее необходимо перенести

днзчение силы тяжести в точку Б при помощи редукции в свободном воздухе

л , д

ВС

В результате определено значение силы тяжести, которое было бы в точке Б

•рн отсутствии внешних притягивающих масс; дд/дп — вертикальный градиент

действительной силы тяжести.

Для получения значения силы тяжести в точке Б, которое бы наблюдалось

•ра наличии внешних притягивающих масс, следует ввести поправку Ад'

и влияние этих масс на значение силы тяжести в точке Б, вычисляемое по

+>рмуле (УП.З).

В общем случае Ад Ф Ад', поскольку вычисление влияния притягивающих

шее производится в разных точках (в первом случае — в точке В, во втором

случае — в точке Б). Окончательно будем иметь

. , . д

ВС

&> = 6п =

Яв

—Д*—А* + —2 '

Отсюда видно, что для получения значения величины д

необходимо знать

»лкон распределения плотностей внешних масс и вертикальный градиент дей-

ствительной силы тяжести. Поскольку ни то, ни другое точно неизвестно,

•риходится идти на упрощения. Так, при вычислении редукции Прея при-

вжмается дд/дп = ду/дп = 0,3086 мгл/м, а поправка за влияние внешних

кзитягивающих масс вычисляется как притяжение плоского однородного

ВС

кжлпндра, для которого Д^ = Ад' = 0,0418 б —.

В таком случае

ёв = §в + Ад

ВС вс

гзе Ад

= +0,3086 2 X 0,04186 -у. Эта величина называется редук-

сгей Прея.

Способ, предложенный Нитхаммером, испытан В. Ф. Еремеевым на раз-

лжчных моделях. Оказалось, что основную часть погрешности вносит исполь-

»эвание нормального градиента силы тяжести, так как при этом остается не-

учтенным влияние внутренних аномальных масс. Разумеется, что незнание

точного закона распределения плотностей во внешней массе также вносит допол-

нительные ошибки. Для трех моделей Еремеева общие погрешности способа,

предложенного Нитхаммером, составили заметную величину (0,5; 1,3; 0,1 м).

Таким образом, поскольку плотность внешних масс и аномалия вертикаль-

вого градиента силы тяжести, вызванная внутренними аномальными массами,

т;чно неизвестны, ортометрическая высота не может быть точно вычислена.

249'