Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

(ё — Т)ср — среднее из аномалий в соседних точках А и В; у

— сред,

значение нормальной силы тяжести.

Выражение (1Х.27) в точности совпадает с (IX.13).

Полученными формулами можно пользоваться и при сравнительно болы

расстояниях между реперами А и В, однако при этом должно быть изве<

расположение нивелирной линии, ее профиль, хотя бы приближенно сня: з

с карты вдоль нивелирной линии, и должна иметься детальная гравимет г

ческая карта.

Согласно Инструкции

величина у

принимается постоянной для в» *

территории страны и равной 980 ООО мгл. Значение Н

ср

определяется по даннь.»

предварительных вычислений и округляется до целых метров. Геодезичес:- -

широты реперов для определения у

определяют по топографической к..""

с точностью до 0,1'.

Для вычисления значения (§ — у)

ср

необходимо сначала определить ве-гт

чины {§ — у) на каждом репере. При этом возможны три случая:

1) имеются данные измерения силы тяжести § на каждом пункте ннь,-

лирования;

2) значения силы тяжести § на пунктах нивелирования не измеряли^.

но на район нивелирования имеются гравиметрические карты аномалий Б]

(как правило, на равнинные и всхолмленные районы);

3) на район нивелирования имеются лишь гравиметрические карты аг

малий в неполной топографической редукции (как правило, на горные и высо-

горные районы).

В первом случае величины § вычисляют по результатам гравиметрически:

определений, а у — вычисляют по формуле

<у

= у

+ Ду,

где Ау — поправка, определяемая формулой (VII.2).

Во втором случае применяется метод косвенной интерполяции с помощи

•

аномалий Буге и аномалия в свободном воздухе вычисляется по форму

•

(VI

1.25).

В третьем случае косвенная интерполяция выполняется с помощью аъ

малий в неполной топографической редукции и аномалия в свободном возду

определяется по формуле

(*-Т) = (*-Т)н.т.р + 2я/В#-Аг

Поправку за рельеф Д#

вычисляют при помощи палетки Лукавченг

и рассчитанных для нее критических таблиц.

Приведем пример вычисления разностей нормальных высот в случае, ког;

аномалии силы тяжести получены по гравиметрической карте аномалий в неп<:

ной топографической редукции (табл. 12). Пример заимствован из Инструкди

Когда нивелирный ход проходит вдоль полигона АБС ... N

имеет ЗЕ,

чительную протяженность, то разность высот между каждой парой репер*

находят по формуле (IX.27), а разность высот конечной и начальной точ-

хода по формуле

Н1-Н1

Д^изм

+ 2 м-С

) 2 <

1Х

•

А А А

«Инструкция по вычислению нивелировок», М., «Недра», 1971.

260'

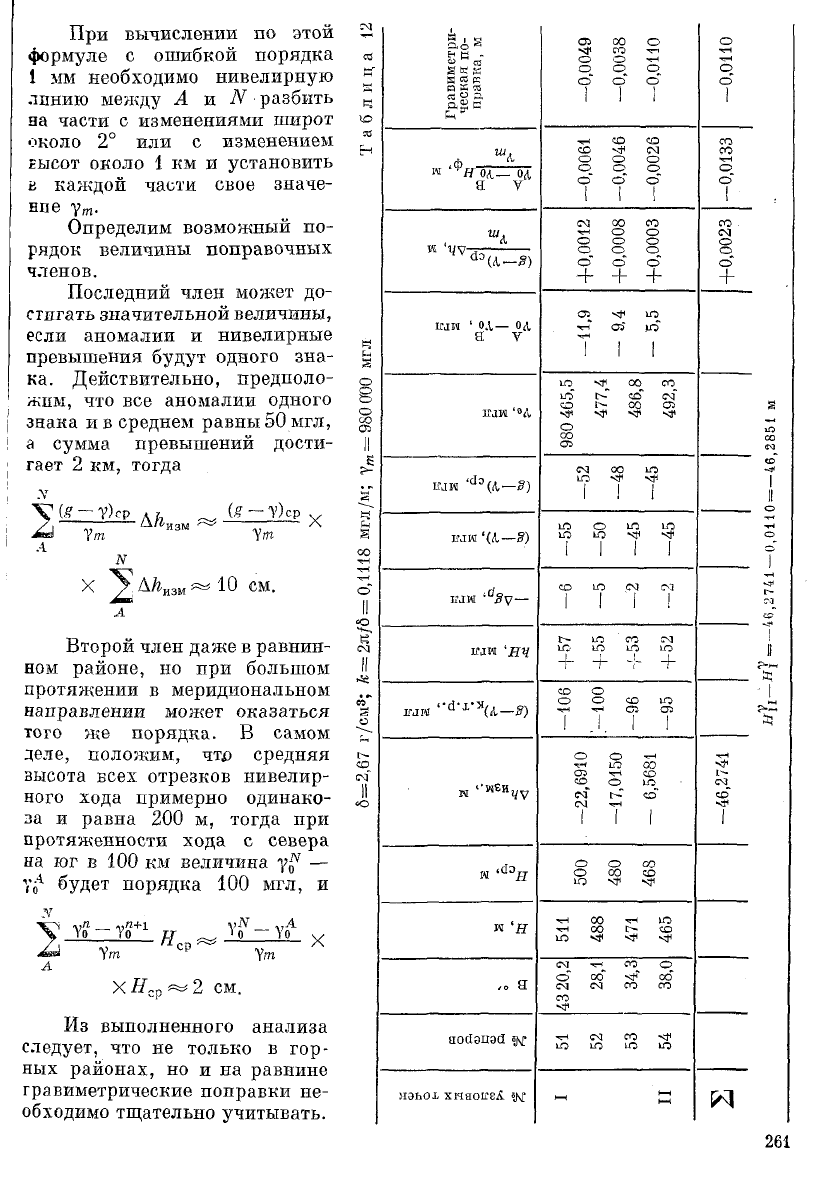
При вычислении

по

этой

формуле

ошибкой порядка

мм

необходимо нивелирную

линию между

А и

•

разбить

на части

изменениями широт

около

2°

или

изменением

высот около

км

установить

в каждой части свое значе-

ние

Определим возможный

по-

рядок величины поправочных

членов.

Последний член может

до-

стигать значительной величины,

если аномалии

нивелирные

превышения будут одного

зна-

ка. Действительно, предполо-

жим, что все аномалии одного

знака ив среднем равны50 мгл,

а сумма превышений дости-

гает

км, тогда

(8 —

у)ср

Ут

Д/г

АК

О? — У)ср

Ут

см.

Второй член даже в равнин-

ном районе,

но

при

большом

протяжении

меридиональном

направлении может оказаться

того

же

порядка.

самом

деле, положим,

что

средняя

высота всех отрезков нивелир-

ного хода примерно одинако-

ва

равна 200

м,

тогда

при

протяженности хода

севера

на

юг

100 км величина у{*

—

То

будет порядка

100

мгл,

Л'

ГС

•

го

Ут

хн

н,

•о

У0

ср

•

Ут

•2

см.

Из выполненного анализа

следует,

что не

только

гор-

ных районах,

но

на равнине

гравиметрические поправки не-

обходимо тщательно учитывать.

«о

Гравиметри-

ческая по-

правка,

—0,0049

-0,0038

—0,0110

-0,0110

И 01—

од,

—0,0061

-0,0046

—0,0026

—0,0133

К чч-;

+0,0012

+0,0008

+0,0003

+0,0023

щи '

ох—

ох

ОЗ

С5

1 1

каи '«Л,

980

465,5

477,4

486,8

492,3

щи '

°(Х—Я)

СМ

00 ю

1 1

1ШИ

—8)

о ю ю

ю ^

1 1 I

и»

—

СО

см

<м

I I !

иди 'нч

»•

Ю СО

см

1С-

ю о ю

+ + +

1ГЛМ

(Х—8)

со

о со ю

•чгн

тн

СЬ

.!. 1 1

и '"

иЕи

уV

-22,6910

-17,0150

6,5681

-46,2741

ОО

00 со

-СР

'Н

^ч

ОО

1>-

СО

ч!< ^

,»

4320,2

28,1

34,3

38,0

аойзпэй

со ^

ю ю ю

ЛЭЬОХ ХНЯ01ГЕА

«дт

1—1

261'

Если нивелирование выполняют вдоль замкнутого полигона АВСЬ

разность высот, вычисленная по формуле (IX.25), должна

быть

рави

и выражение для теоретической невязки имеет вид

М„™ =

ИЗМ И

Ут

А А

В этом случае формула (IX.28) принимает вид

о=2 +2 (уо - тг

)

•+

2 V

Отсюда следует, что теоретическая невязка нивелирования в замки

полигоне должна подчиняться условию

А А

Оценим величину возможных расхождений между поверхностями гес;

и квазигеоида. Расстояние между точками геоида и квазигеоида С и С'

рис. 53) можно подсчитать по формуле

СС' = 1-1'ш*±-{Тс-Т

), (IX

где Тс — значение возмущающего потенциала в точке геоида; Тв — значе-:

возмущающего потенциала в точке физической поверхности Земли В.

Если Тс = Тв, то С С' — 0 и поверхности квазигеоида и геоида совпада

:•

Это имеет место на поверхности океана.

Поскольку, как указывалось ранее, вычислить точное значение пог

циала на поверхности геоида невозможно, об отступлениях геоида от ква:

геоида можно судить лишь по разностям ортометрических и нормальных выс -

Согласно рис. 53 следует, что

СС' = Н

в—Н1.

Для определения этой разности напишем тождество

поделив все члены этого тождества на получим

н% = Ш. =нъ - ^А НЪ, (IX.:-.

8т 8т

отсюда

СС' НЪ.

8т

Положим, что средняя величина аномалии у

— д

достигает 500 у

высота Н

= 4 км. В этом случае

-8т М.

8т

262

При у

— д

= 50 мгл, Ю = 500 м этот член оказывается равным 2,5 см.

Таким образом, на океанах и всюду, где Тс = Тв — поверхности квази-

геоида и геоида совпадают. На равнинах расстояние между этими поверхно-

стями составляет всего несколько сантиметров и лишь в горах максимальное

отступление геоида от квазигеоида может достигать 2 м.

§ 55. ИНТЕРПОЛИРОВАНИЕ АСТРОНОМО-ГЕОДЕЗИЧЕСКИХ

УКЛОНЕНИЙ ОТВЕСА

Прежде чем рассматривать вопрос об интерполировании астрономо-геоде-

зпческих уклонений отвеса, установим различие между гравиметрическими

определяемыми через аномалии силы тяжести) и астрономо-геодезическими

уклонениями отвеса.

В общем случае уровенный элли-

псоид может отличаться от референц-

эллипсоида не только размерами и фор-

мой, но и ориентировкой в теле Земли.

Поэтбму при переходе от гравиметриче-

ских уклонений отвеса к астрономо-гео-

лезическим, или наоборот, приходится

учитывать составляющие углов между

нормалями к референц-эллипсоиду и к уро-

ненному эллипсоиду в плоскости мери-

диана А| и в плоскости первого верти-

кала Ат).

Эти составляющие находятся из со-

отношений

Тк

\ \

ль

у/П

Рис. 56

А| = ^АГ - ёгр.в - 0,17№зт 25;

Дг] ='Паг — т1

грав

Иногда необходимо знать составляющую уклонения отвеса Фаг в произ-

вольном азимуте. Спроектировав составляющие в меридиане и в первом вер-

тикале на данное направление, получим

•&АГ

= ^АГСОЗ Л + Г|

АГ

81ПЛ. (IX.33)

Составляющая в произвольном азимуте А угла между нормалями к рефе-

ренц-эллипсоиду и уровенному эллипсоиду определяется по формуле

АГ

-й

грав

•0,171'Я*эт 25 соз А.

(1Х.34)

М. С. Молоденский разработал оригинальный метод, позволяющий интер-

полировать астрономо-геодезические уклонения отвеса между пунктами, в кото-

рых они известны, используя местную гравиметрическую съемку.

Пусть астрономо-геодезические уклонения отвеса известны в нескольких

точках А, В, С, Б .. . некоторой небольшой области а (рис. 56). Требуется

получить астрономо-геодезическое уклонение отвеса в произвольной точке К

области о. На основании (IX.34) астрономо-геодезическое уклонение отвеса

можно представить как сумму гравиметрического уклонения отвеса и составля-

ющей угла между нормалями к референц-эллипсоиду и уровенному эллипсоиду

ФАг(#) = Фг

ав(Я) + ДФ(#).

263'

Если всю поверхность Земли разделить на две зоны: центральную зону_

в пределах которой имеется гравиметрическая съемка, и зону 2'>

кото*- г

относится вся остальная часть поверхности Земли, где аномалии силы тяже:

могут быть неизвестны, гравиметрическое уклонение отвеса можно представ*...

в виде

^грав(К) = г%

рав

(2, К)+Ъ грав (2', к),

где первое слагаемое определяется только аномалиями в области 2>

а ВТ0

зависит от аномалий в области 2'-

Следовательно,

•&АГ

(К) = -&

грав

(2, К) +

рав

(2', К) + М (К). (IX.

Первый член правой части известен и вычисляется по формуле (VIII.

методом численного интегрирования, причем пределы интегрирования оп:-

деляются пределами области 2- Д

ва

ДРУ

ГИХ

члена, стоящие в правой чаг

(IX.35), для произвольного пункта К неизвестны.

М. С. Молоденский предложил выбрать размеры зоны 2 таким образ*

чтобы сумма "&

рав (2') + ДФ внутри области <т менялась по линейному закону

В таком случае эту сумму можно линейно интерполировать между пунктам

в которых она известна. В каждом астрономо-геодезическом пункте области

(.А, В, С, В...) эта сумма известна, поскольку, например, для пункта А на! осг

вании (IX.35) имеем

<>ггав(2', 4)+ДвИ) = вАгМ)-#п,ав(2, А).

Таким образом, в способе Молоденского линейной интерполяции подлей*

не сами астрономо-геодезические уклонения отвеса, а лишь разности меж:"

астрономо-геодезическими и гравиметрическими уклонениями отвеса, обусл

вленными влиянием аномалий зоны 2.

Линейная интерполяция разности астрономо-геодезических и гравимет;

ческих уклонений отвеса обосновывается следующим образом. Угол ДФ межг

поверхностями эллипсоидов изменяется очень медленно и плавно, а влиянг

аномалий зоны 2' на уклонения отвеса в пунктах, находящихся в предел;

области а, можно свести к меняющимся по линейному закону, выбрав зону *

достаточно больших размеров по сравнению с областью ст.

Задача при этом заключается в том, чтобы при заданных размерах области

определить минимальные размеры зоны 2> обеспечивающие необходимую

точность интерполяции уклонений отвеса. Для решения задачи достаточн

оценить предельную ошибку результата в зависимости от радиуса области I

внутри которой аномалии силы тяжести известны.

Рассмотрим общий случай интерполирования по двум координатам. В»

берем начало О системы прямоугольных координат х, у в центральной част

области а (см. рис. 56). Граница областей 2

должна быть настолько у~

лена от границы сг, чтобы минимальное расстояние от точки О до внешней гр^

ницы 2 было больше максимального расстояния от той же точки О до границ;

области а (отношение этих расстояний должно быть В/1 ^ 2).

При этом условии значение Ф^ав (2 » Ю

произвольной точке К области

можно представить рядом

*П«(2\ *) = »грав (2', V . .

264'

в котором члены разложения являются линейными относительно координат.

В случае учета при линейной интерполяции только этих членов ошибка ин-

терполированного значения "&

грав

(2\ К) определится величиной последующих

членов, зависящих от вторых и высших степеней координат. Исследование

этих членов позволяет определить границу между областями 2 и 2'» Д° которой

необходимо учитывать аномалии силы тяжести.

Предельную величину этих нелинейных членов позволяет оценить формула,

полученная М. С. Молоденским

6< , (IX.36)

где р = В/1 (Е — радиус зоны 2> I ~ Р

зоны а); — у)

— среднее

квадратическое значение аномалий вблизи границы зон 2

2'-

Задаваясь величиной ошибки б линейного интерполирования б 0,3"

при (^ — у)

= 15 мгл, получим р = 3.

В конкретных условиях при оценке (§ — у)

нужно использовать грави-

метрическую карту. В частности, в равнинных районах среднее квадратическое

значение аномалий достаточно мало, поэтому можно ограничиться значением

р = 2.

При вычислении астрономо-геодезических уклонений отвеса по методу

М. С. Молоденского возможны два случая интерполяции: по площади и по пря-

мой линии.

При интерполировании по площади точек с известными астрономо-геоде-

зическими уклонениями отвеса должно быть не менее трех. Если точек больше,

появятся избыточные измерения, которые при обработке по способу наимень-

ших квадратов позволят снизить случайную часть ошибки результата. Для

интерполирования по прямой достаточно иметь две точки на концах отрезка.

Рассмотрим первый случай. Представим разности астрономо-геодезиче-

ских и гравиметрических уклонений отвеса как линейные функции координат

(ф и X) точки, лежащей внутри области а

БАГ" 1грвв(2)=«Ф + М +

1 /тлготч

(' (1Х.О/)

Лаг —

Пграв

Ш = «Ф + + У )

где а,

Ъ,

с, а, р, у — коэффициенты линейной зависимости.

Эти коэффициенты для данной области а при наличии более трех пунктов,

не лежащих на одной прямой, для которых известны и астрономо-геодезиче-

ские и гравиметрические уклонения отвеса, находят по способу наименьших

квадратов, поскольку каждый такой пункт (например, А) позволяет составить

два уравнения

т^г - ^

рав

(2) = Оф

+ р+у,

где верхним индексом А обозначены величины, вычисленные для этого пункта.

После того как коэффициенты а, Ь, с, а, Р, у для данной области определены,

можно вычислить интерполированное астрономо-геодезическое уклонение от-

веса в любой точке К области сг по формулам

5ннт(^) = ?грав(1, К)+а

+ЪХ

+С |

265'

Точность интерполированных уклонений отвеса зависит от ошибок ог

деления гравиметрических уклонений отвеса, обусловленных влиянием

малий в зоне 2» ошибок определения интерполяционных коэффициегг

а,

Ь,

с, а, р, у и координат пункта

и X, а также от заданной величины ошибк:

линейного интерполирования.

Рассмотрим случай, часто встречающийся в практике, когда иитерпог

рование уклонений отвеса производится по линии АВ (вдоль ряда триангу

ции). Итак, пусть А и В — астропункты, в которых известны Фаг (4), -

^грав (2» -4)

^грав (2, В). Требуется вычислить интерполированное уклонег

отвеса в пункте Ь.

Линейно интерполируя разности ^дг —

9'грав(2)

на

Участке АВ, полу

дг

(-4)

— "грав (2, А)] +

, РаГ (В) - а

рав (2. Д)] - [Од

И) - ^рав (2'

)

Н 21

где 21 — расстояние АВ между астрономическими пунктами А и В; з — р

стояние пункта Ь от начального астрономического пункта А.

После преобразований получим

+ [^АГ(5)-Ф

грав

(2, В)}^.

Определим ошибку интерполированного уклонения отвеса.

Считая, что ошибки гравиметрических уклонений отвеса в пунктах .

В и Ь имеют один порядок ти пренебрегая ошибками астрономо-геодезич-

ских уклонений отвеса, найдем

*Ч

пяТ

= т^ У2(1-к + к*),

где

В среднем можно считать [14], что ошибка интерполированного уклон-

ния отвеса

Ошибка гравиметрического уклонения отвеса зависит от размера облас-

интегрирования, плотности гравиметрической съемки, точности определенл

аномалий силы тяжести и высот гравиметрических пунктов.

Считая, что ошибка гравиметрического уклонения отвеса ?п^ = ±0..

получим по (IX.39) та^ = ±0,6".

В настоящее время гравиметрические уклонения отвеса можно получи:

с точностью ±0,1—0,2", однако точность интерполированных уклонена

отвеса пока что лимитируется точностью астрономических определений.

266'

§ 56. ВЫЧИСЛЕНИЕ ПРЕВЫШЕНИЙ КВАЗИГЕОИДА

ОТНОСИТЕЛЬНО РЕФЕРЕНЦ-ЭЛЛИПСОИДА

Установим зависимость между элементарным превышением точки земной

вверхности над референц-эллипсоидом

йНлт

и нивелирным превышением йк.

Пусть М (рис. 57) — точка земной поверхности, имеющая геодезическую

Шсоту Ядг! К — бесконечно близкая к М точка в направлении I, составля-

ющем с меридианом угол А. Геодезической высотой точки К в этом случае будет

1Гдг + (Шаг. Обозначим составляющую астрономо-геодезического укло-

нения отвеса в направлении I через Фаг- Тогда отрезок МС отвесной линии

•ежду уровенными поверхностями, проходящими через точки М и К, — ниве-

•мрное превышение йк, а отрезок МБ—

аиементарное превышение йН^т- Обо-

«ачим В К через й1.

Из рис. 57

МС = МЕ + ЕС,

МЕ = МП

сое

Фаг = ^Я

АГ

соз

Фаг,

ЕС — КЬ—й1 зтФ

АГ

МС = йк,

поэтому

йк —

йНхт

соз Фдг + яш Фаг-

По малости угла Ф

г можно положить соз ^аг = 1, зт гг

лг

= п

АГ

Окончательно

йН

А г

=йк— Ф

АГ

й1.

(I Х.40)

Величина йк в этом выражении определяется из геометрического нивелиро-

вания, а член Фдгй1 в результате так называемого астрономического нивели-

рования.

Из формулы (1Х.40) видно, что приращение высот точек физической по-

верхности Земли над референц-эллипсоидом равно нивелирному превышению

плюс поправочный член, учитывающий изменение направления отвесной линии

относительно референц-эллипсоида.

В настоящее время нет необходимости иметь геодезические высоты Н на каж-

дой станции геометрического нивелирования. Для целей высшей геодезии

необходимо знать геодезические высоты Н на пунктах триангуляции 1 класса,

в которых приращения нормальных высот надежно определены методом гео-

метрического нивелирования. Поэтому целесообразно получить формулу для

вычисления приращений высот квазигеоида над референц-эллипсоидом, или

формулу астрономического нивелирования высот квазигеоида.

Вычислив превышения квазигеоида Л^аг между пунктами триангуляции,

начиная от исходного пункта, где высота квазигеоида известна (в частности,

для Пулково принято Со

0), очевидно, можно получить значения самих вы-

сот квазигеоида и, следовательно, профиль его поверхности относительно по-

верхности референц-эллипсоида. При выводе формулы для вычисления элемен-

тарного превышения квазигеоида над референц-эллипсоидом введем местную

267'

систему прямоугольных координат х, у и Н, считая, что Н совпадает с нап:

влением нормали к референц-эллипсоиду. Тогда

Поскольку

д1 „

дх ~ ду ~~

Т1

Преобразуем 81!дН. Из (VI.21) получим

дГ, __ 1 дТ Т ду _ 1 / ОТ 1 ду

дН ~ у дН 72 дН ~~ у \ дН у дН ) '

В соответствии с краевым условием (VIII.5) при Ш

= 17

выражение, стояшл

в скобках, представляет собой аномалию силы тяжести (§ — у). Таким образом.

81 е~у

дН У '

Следовательно,

-ЙБ = I<1х + п йу + ^-Ш,

разделим и умножим сумму (Ых + г\йу) на й1, где

= йх

+ йу

Тогда

Поскольку

Ах л Ау • л

ЧГ

=С05А

> Ж=

5шА

получим

—йЪ

сов

А +

Т]

зт А)

й1

+ Ш.

Выражение, заключенное в скобки, представляет уклонение отвеса в азимуте А

[см. формулу (IX.33)3

Фаг = !

соз

4 +

т} 81П

А. '

Окончательно

= + . ^(1Х.41(

Проинтегрировав выражение (1Х.41) вдоль звена триангуляции между

астрономическими пунктами А и В, получим

в в

А А

Формула (IX.42) принципиально решает вопрос об определении превыше-

ний квазигеоида. Первый член правой части является главным, второй — ма-

лой поправкой за непараллельность уровенных поверхностей. Если при вы-

числении главного члена

Фаг^ использовать лишь астрономические опре-

268'

деления ср и Я в достаточно близких пунктах А и В, то нивелирование такого

рода будет называться астрономическим.

Для вычисления интеграла ] Фаг^ необходимо знать функциональную

зависимость между величиной Фаг и координатами текущей точки. При

астрономическом нивелировании делается предположение о линейном харак-

тере этой зависимости.

Так, если начало координат поместить в точке А (см. рис. 56), а расстоя-

ние текущей точки Ь от начальной А обозначить через х, то

(В) ~ ,

(А)

ФАГ (Ц = ФАГ (А) +

АГ

АТ

где 21 = АВ — расстояние между астропунктами.

Подставляя это значение Фдг в первый член правой части формулы

(IX.42), получим

г г' (В)

—•&

(А)

\ ФАГ 61 = ФАГ (А) \ 6х +

Ат(

' ^

ктК

^ х6х = I [Ф

АГ

{А) + Ъ

ат

(В)],

АО О

(1Х.43)

где

Если расстояние АВ между астрономическими пунктами порядка 70—

100 км (как это имеет место в триангуляции 1 класса СССР), то точность вычи-

сления ] Фаг^ по (IX.43) будет недостаточна. Для сравнительно надежного

вычисления превышений квазигеоида методом астрономического нивелирова-

ния необходимо, чтобы расстояния между астропунктами в горных районах

не превышали

—2 км, а в равнинных районах были не менее среднего расстоя-

ния между пунктами триангуляции.

Однако и при таких расстояниях между астропунктами нельзя быть уве-

ренным в линейном характере измерений уклонений отвеса.

Астрономическое нивелирование, вообще говоря, является достаточно

трудоемким процессом, поскольку при применении этого метода необходимо

часто производить астрономические наблюдения. Астрономическое нивелиро-

вание получило широкое распространение в странах Западной Европы и США.

Так, почти для всей территории Северной Америки превышения квазигеоида

определялись этим методом, а построенный по 35-й параллели северной широты

профиль высот геоида имеет протяженность 4000 км.

Методика определения интерполированных уклонений отвеса, разрабо-

танная Молоденским, обеспечивает необходимую точность при достаточно ред-

кой сети астрономических пунктов (при расстояниях между пунктами порядка

70—100 км).

При этом предполагается, что вдоль звена триангуляции по линейному

закону изменяются не сами уклонения отвеса (как это считается при астроно-

мическом нивелировании), а лишь разности Ф

г — Фграв (2)- Интерполиро-

ванное уклонение отвеса Фаг в любом промежуточном пункте звена А В

получается как сумма двух величин: Ф

гра

в (2), определяемой по результатам

269'