Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Координаты ВжЬ входят в неявном виде в функцию Стокса 8 (тр). Это

вытекает из формулы (111.17), заменив в которой 0 через 90° — В, получим

соз ар

= зт В

зхп

В' +

соз

В соз В' соз (Ь'

—

Ь).

Следовательно, можно написать

(VIII.54

Г\

= .

4яу

О Л

уь

1 ГГ/.. л ^ Зф

4лу

Цт-у)

йг|) сое В дЬ

(1(0.

Для определения частных производных, стоящих под интегралами, вос-

пользуемся формулами сферической астрономии, которые в соответствии

с рис. 21 представим в виде

81П яр

зт А =

соз

В' зт

{Ь"

— Е)

зт

1р соз

А зт В' соз В —

соз

В' зт В соз (Ь' — Ь)\'

(VIII.55)

где А —азимут направления на текущую точку с координатами (В', Ь'), из

данной точки (В, Ь).

Дифференцируя (VIII.54), по В и Ь, получим

—зт

гр

= зт В" соз В

— соз

В' зт В соз (Ь" — Ь),

-зтар^

= СОЗ

В'

СОЗ

81П

(Ь' — 1).

Принимая во внимание формулы (VI 11.55), будем иметь

^ л

ТТГ

= соз А

дБ

81И

(УШ.5б!

соз В

дЬ

Используя эти соотношения, представим | и г) в виде

4117

Ииг-т)

дурр)

а\р

соз А

(1(0

(VIII.57)

Эти формулы были получены Венинг-Мейнесом и носят его имя. Если

выражать составляющие уклонения отвеса в секундах дуги, то

о о

Я 2Я

-ч-и*-^®

4.ту 81П

о о

8^плр^ зт А

й\р <2А.

200'

Введем обозначение

() = ~

Л8 (ф)

2у

8111

1" |)

81П

(УШ.58)

:-та функция называется функцией Венинг-Мейнеса.

Окончательно получим

о о

я 2я

(УШ.59)

Дифференцируя функцию Стокса (VIII.38), найдем

г|)

рпе '

-5 81П

1|3

— 3 С08у+ 3 8тг|)1п (з1П 31П

—

1 СОЗ 1|3

СОВ

81П

СОЗ

-у)

Проведем алгебраические преобразования

й8

(Ч>)

ау

81П1|5 = С08

- созес

-у — 6

81П

+ 20

81П

-у +

+ 12зш

|-1

(зт|. + 8т

^)-

3 соз (1 + 2

81П

:реобразуем последний член, стоящий в скобке,

Зсозг|> (1 + 28Ш

3 б8

ш-1^1_8т-|- —2зш2-|-)

+ 8111-

+ ЗШ-|-

вйп|-(1-2йп4.)

81П

+ 8т^|-

+ 6

81П

-у

окончательно

81П — -СОЗ

± [созес -1 +

12 8Ш

±- 32 81П

+ ——-—^ —128ш

-у

1п

(зш|- + 8т

4-)]. (У1И.60)

201

Таким образом, функция Венинг-Мейнеса

V м = -^ТПГГ

соз2

1 [

созес

т + зт - 32 эт* ± +

+ Ц:

-12 8ш^1П (УШ.61)

1+8111-5-

Числовые значения функции (} (гр) приведены в табл. И.

Т аб лица 11

7 = 979,77 гал*

г|)°

Я Я

с\о

+0,22

130

-0,34

+12,35

+0,03

140 -0,24

+1,59

-0,15

150

—0,16

20 +1,02 90 -0,29

160 —0,08

30 +0,79 100 —0,38 170

—0,02

40 +0,61 110

—0,41

180

0,00

50 +0,43 120

-0,40

0,00

* Для V взято среднее значение нормальной силы тяжести по всей Земле, определяемое формулой

Гельмерта 1901 — 1909 гг.

Функция (гр) непрерывна во всей области 0° гр ^ 180°, кроме точки

гр = 0°. С увеличением значения функции () (гр) быстро убывают и при гр ^

70° (? (гр) = 0. Затем функция (} (гр) принимает отрицательные значения,

убывая до —0,41 при гр=110° и далее возрастает до 0 при гр = 180°. Эти осо-

бенности изменения функции () (гр) учитываются при вычислении | и

т]

мето-

дами численного интегрирования.

Формулы Стокса (VIII.53) и Венинг-Мейнеса (VIII.59) следует рассматри-

вать как первое приближение к определению высоты квазигеоида и составля-

ющих уклонения отвеса в точках физической поверхности Земли.

§ 46. ОПРЕДЕЛЕНИЕ ВОЗМУЩАЮЩЕГО ПОТЕНЦИАЛА ЗЕМЛИ

НА ЗЕМНОЙ ПОВЕРХНОСТИ (РЕШЕНИЕ МОЛОДЕНСКОГО)

Краевое условие для возмущающего потенциала, полученное М. С. Моло-

денским для поверхности 2 (VIII.8) с учетом (VIII.6), имеет вид

где индексы 2 и 8 означают, что соответствующие величины относятся либо

к поверхности Земли первого приближения 2, либо к физической поверх-

ности 8.

В качестве исходной уровенной поверхности нормального потенциала

берется сфера радиуса В и считается, что радиус-вектор точки на поверхности 2

равен

Рх = В+Н1.

202'

Проблема состоит в определении функции Т, которая на поверхности 2

удовлетворяет условию (VIII.62), вне Б является гармонической функцией

координат и на бесконечности регулярна. М. С. Молоденский предложил

рассматривать возмущающий потенциал во внешнем пространстве как потен-

циал простого слоя плотности ф, распределенного на поверхности 2,

-И*

<22.

(УШ.бЗ)

В таком случае задача сводится к определению функции ф. Внешнюю

производную потенциала (VIII.63) на слое 2 по направлению Н получим ана-

логично (VIII.41)

' (ЭТ.)

V дН )п->1Г<

СОв(г, НУ) IV

Ф , — 2яф

соз

а,

(VIII.64)

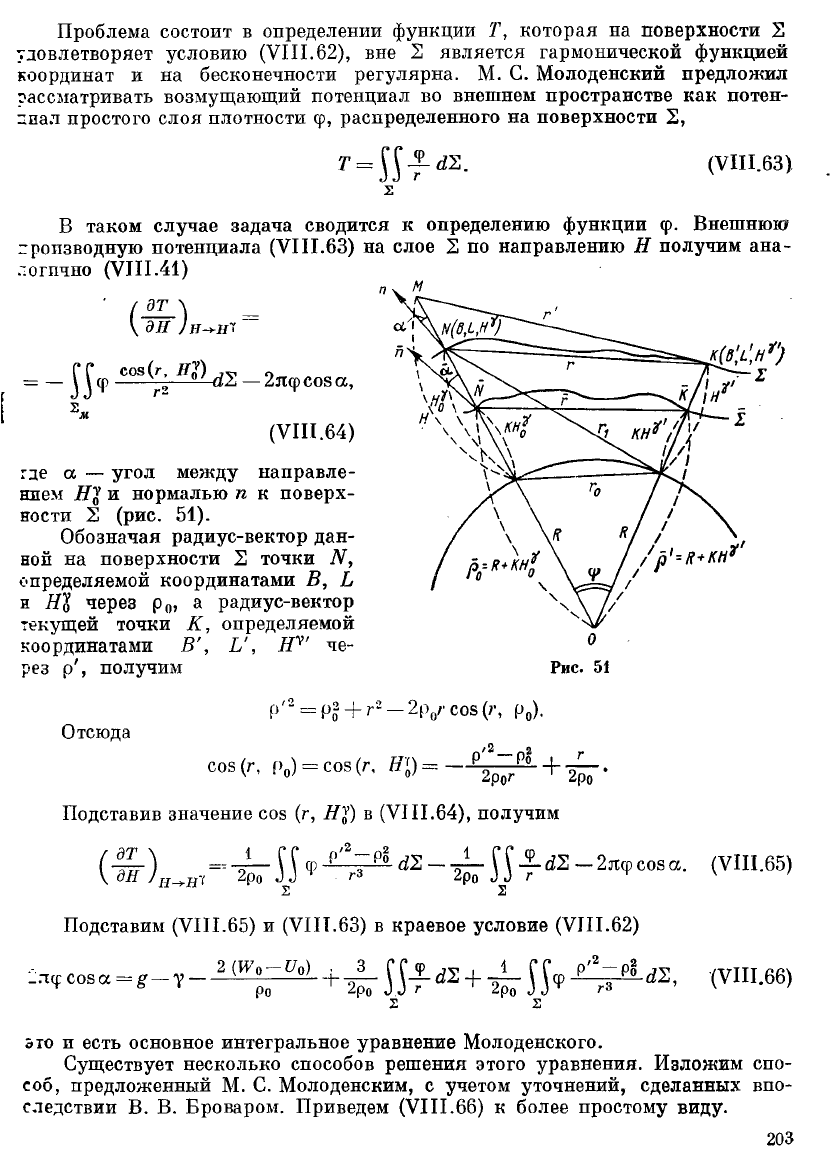
где а — угол между направле-

нием Щ и нормалью п к поверх-

ности 2 (рис. 51).

Обозначая радиус-вектор дан-

ной на поверхности 2 точки N,

определяемой координатами Б, Ь

н Н1 через р

, а радиус-вектор

текущей точки К, определяемой

координатами В', Ь', Я

' че-

рез р', получим

Отсюда

р'

+ г

-2р

лсоз(;\ р

соз (г, р

) = соз(/\ Щ) =

•Ро

2ро г

2ро

Подставив значение соз (г, Ну) в (VIII.64), получим

\дН )

Н^-Н'1

2ро

ф-

-Р8

гЗ

Й2 —у- Л^-й2-2лфсоза. (УШ.65)

2 2

Подставим (VIII.65) и (VIII.63) в краевое условие (VIII.62)

. з ("Сш ^ се п'

-п?

_лф

соз

а = д — у

•

Ро

2ро

это и есть основное интегральное уравнение Молоденского.

Существует несколько способов решения этого уравнения. Изложим спо-

соб, предложенный М. С. Молоденским, с учетом уточнений, сделанных впо-

следствии В. В. Броваром. Приведем (VIII.66) к более простому виду.

203'

Учитывая, что р' = В + № , р

= Д + Щ, а р' - р

= Н

- Щ.

выражение, стоящее в последнем члене уравнения (VIII.66), можно представить

как

р'

-р§ _ (я

'-Я

)(р'+Ро) 2ро(Я*'-Яг) + р'(Я

-ЯУ)-ро(Я*'-ЯУ)

2р о/"

2р

гЗ 2р

гЗ

—

_ Я^-ЯУ р'-ро) Я^-Я? , ^ТТТЙ-

—

г» "" 2^75 — Г " ^ '

Используя обозначение

перепишем уравнение (VIII.66) в более простом виде

(УШ.68,

Введем вместо плотности слоя <р вспомогательную функцию %, связанную

с ф соотношением,

__ Я»

—

соз

ос.

Элемент Й2 поверхности 2 заменим элементом телесного угла йо)

2 соз а

асо

= .

Р'

Элемент массы слоя будет равен

Ф <1'^ = П

%<1(о,

а интегральное уравнение (VIII.68) примет вид

2л% соз

ос

= 8§

+ ^

йсо

Ь> 0)

Выразим возмущающий потенциал Т через функцию %

(VIII.70)

М. С. Молоденский предложил следующий метод решения. Поверхность 2

преобразуется в поверхность 2 так, что угловые координаты в полярной си-

стеме координат сохраняют свое первоначальное значение, а радиус-вектор

(см. рис. 51) изменяется в соответствии с выражением

р = В + к(р~В) = В+Ш

, (VIII.71)

204'

где

р.

— радиус-вектор преобразованной поверхности 2; к — постоянный коэф-

4пцпент. Очевидно, что при к = 1 поверхности 2 и 2 совпадают, а при к = О

преобразованная поверхность 2 совпадает с поверхностью сферы. В общем

случае 0 ^ к 1.

При переходе от 2 к 2 элемент йсо не меняется и аномалии 8§

будем

считать отнесенными к новой поверхности 2. Возмущенный потенциал Т на

яовой поверхности 2 будет выражаться через функцию

формулой

Г = (VIII.72)

со

где г — расстояние ЫК между проекцией данной точки N с радиус-вектором

= В + Щ и проекцией текущей точки К с радиус-вектором р' = Е -+- Я

на поверхности 2.

Новая плотность % на поверхности 2 определится уравнением, аналогич-

ным (VIII. 69)

у„ соз

а = 6* + ДО I А» + Д»

ДО

* *» +

СО

+ (УШ.73)

со

где а — угол между нормалью к поверхности 2 и радиус-вектором р

в точке N.

Величины г и ос являются функциями к и могут быть представлены в виде

рядов по степеням к.

Для поверхности сферы (см. рис. 51) имеем

= 2Е зт у,

где — угол между р_о_и р'.

Для поверхности 2 можно написать

= р« + Р

- 2р

р' соз

41)

= (Е + кН1)

+ (В + кН

)

- 2 (В + кЩ) (В + кН

) соз

г}>.

После преобразований

+ к

я?

' +

+ к

{ВТ - Но)

г2

НУ

Если пренебречь малыми порядка —то

Я ' Я 2

ЧУ

г%

+ к

(Н

-НЪ)

г%

(1 + к

), (VIII.74)

где

н^'-Щ

и =

Го

Это упрощение вполне оправдано, так как само интегральное уравнение

(VIII.73) имеет относительную погрешность порядка сжатия Земли а вслед-

ствие того, что за отсчетную поверхность принята сфера.

205'

Наклон поверхности 2 изменяется пропорционально к, т. е. будет име*

место равенство

1,§а =

к%%<%,

откуда

соз

а = (1 + к

а)"

— 1 — к

1§

а + ... (VIII.:'

Величины Т, % также могут быть представлены в виде рядов по степеням

со

т = 2 к

т„, (VIII.?

п=0

Х = 2 Ъ

%п. (У1П.7-

71=0

Неизвестные функции Т

и %„ полностью определяют искомые на поверх

ности 2 величины Т и поскольку при к = 1 ряды (VIII.76) и (VIII.77) дак:

т =

71=0

со

ЗС

= 2 Ъп.

(УШ.7

(VIII.79

Чтобы определить функциональную зависимость между Т

и %

, подстави:

(VIII.76) и (VIII.77) в формулу (VIII.72), кроме того, функцию 1/г представим

в виде ряда по степеням к, использовав для этого соотношение (VIII.74)

4 = А- (! + =—('1—1 к

+ 4кЫ*-...). (VIII.80

'"'О о /

В результате

со

т = 2 Ъ

=В

. + к

+ к*

+...)

Пе»0

''о

йсо.

Множители при к" слева и справа должны быть равны, т. е.

г.-л'И-й-*»'

га

" /Л "

(УШ.81>

Следовательно, для определения возмущающего потенциала по формуле

(VIII.78) нужно знать %

. Подставим в интегральное уравнение (VIII.73) полу-

ченные ряды (VIII.75), (VIII.77) и (VIII.80)

2я

(Хо

+ Нх +

Хг

• • •)

(1 - к

а +...) =

206'

(й

•

55 (Хо+ кгх + /с

Ха

+...) &

(1-1 /с

+ . ..) Ао.

Перемножая ряды, найдем

2я%

+ 2лЛх1 + 2я/с

+ ... — 2я/с

Хо а +... =

зя

/СХ1 I

кг

''о '"о

+ Д'

'о

+т

, АЗхХг

•Ь •

27-0

3 АЗхЗхо

. . . ^ й© +

2 г1

№хо ,

кЯ

Ул |

го

. . . )й<в +

2 г

Приравнивая множители при к в одинаковых степенях, получим

(В

/Л Л1 О

-щг

АО I о .1.1

'о

пли в общем виде

• м 0) "

Хо Ло

+ 2я 1^

а Хо.

= (VIII.82)

где

2 (Шр-Цр)

Хо"

йсо,

- Т И Ь

+ 2я

Хо

а,

(VIII.83)

207'

Интегральное уравнение (УШ.82) подробно рассмотрено в § 44. Анало-

гично (VIII.44) и (VIII.45) напишем общие решения уравнений (УШ.82) в сле-

дующем виде:

Я"

СО со

(VIII.84»

(VIII.85!

Подставляя (VIII.85) в (VIII.81), получим уравнения для определения Т-

всех степеней

= 1г 11

^ -1

] йсо

со

Г.-^уо*™-!]*.

(ушад

/Л /Л ®

Главную часть возмущающего потенциала Т на земной поверхности дает

первое уравнение, соответствующее к = 0, и, следовательно, а = 0, р = В.

Подставляя значение из (VIII.83), получим

е>

что совпадает с формулой Стокса (VIII.47).

Во все последующие приближения также входит функция Стокса. Рельеф

учитывается со второго приближения, наклоны земной поверхности (углы а)

в явном виде появляются, начиная с третьего приближения (VIII.83).

Наибольшую поправку к решению Стокса дает возмущающий потенциал Т

Если ограничиться только двумя членами Т

и Т

, то

Т = 2 (Ш

~ И

) + Л ДО {§ - у + 6е

) [5

ДО

А» + АьМ..

(

.87)

Для вычисления поправочных членов 6^, . . . служат формулы

(VIII.83). Входящие в правые части этих формул подынтегральные выражения

убывают как 1/гВ или даже быстрее. Поэтому при вычислении . . .

нет необходимости интегрировать по всей поверхности Земли, а достаточно

ограничиться ближайшими окрестностями исследуемого пункта.

208'

Подставив значение Т (VIII.87) в (VI.19), получим формулу Молоденского.

лля вычисления аномалии высоты

4яу

а -

V •+

[8 <ф)

-1]

Ао

+ . (УШ.88)

Условием существования решения интегральных уравнений типа (VI 11.82)-

является требование, чтобы свободный член не содержал сферической функции

первой степени, т. е. применительно к формулам (VIII.87) и (VII

1.88)

аномалии

силы тяжести должны удовлетворять условию

Й +

с03

'фЖ» = 0.

(VIII. 89)

Подставив значение функции У

(6, %) из (VIII.48) в (VIII.88) и полагая

ввиду малости величин х

, у

, г

) }М/В

у, получим

^ _ И^о Цо_ ^

со8

соз

со8

}

81П

В] +

(УШ.ЭО)

Таким образом, для определения аномалии высоты, помимо аномалий:

силы тяжести, необходимо знать четыре постоянные величины

У о,

о»

Алу

Л (8 —Т + бй)Ао

§ 47. ОПРЕДЕЛЕНИЕ СОСТАВЛЯЮЩИХ УКЛОНЕНИЯ ОТВЕСА

НА ПОВЕРХНОСТИ ЗЕМЛИ

Для определения составляющих уклонения отвеса \ и т) в точках физи-

ческой поверхности Земли необходимо слагающие возмущающего потенци-

ала Т — величины Т

, Т

, Г

, . . . подставлять в формулу (VI.8).

Слагаемые в | и т), соответствующие потенциалам Т

, Т

, . . ., обозна-

чим соответственно через ^ |

•

•>

Ло»

1х> Лг»

•

• • Вычислим сначала,

величины

* 1 дТ

ро? дВ '

_ вес В дТ

110

Р^Г ЭЬ '

Дифференцируя формулу Стокса (VIII.47) по переменной В

получим

В д

4яр

'у

•^•ЭДог-т)-^)*»-

Д2р

у дВ

Будем считать

[«о

008

ВСО&1 + У о СОЗ В 81П Ь + 2

81П В\

ро-

14 Заказ 1379 209?