Шимбирев Б.П. Теория фигуры Земли

Подождите немного. Документ загружается.

Поскольку сферическая функция б^о не содержит членов первого порядка,

то по условию ортогональности сферических функций каждый интеграл в от-

дельности должен быть равен нулю. Таким образом, получаем три условия

Л бй, сов е'втв'= О

Лбйсо8Я'8т8'атв'йе'йЯ,' = 0 (VIII. 15)

со

Л 6#

вт Я,'8т0'8т0'й0'йГ = 0

0) )

На основании (VIII.И) будем иметь

Лв

гА(

е', «а.-ДО(,-,»«.(в-, «л-гаг^до ^

При п Ф 0

Л яде', А/)Л» =

(О

(УШ.16)

На этом основании условия (VIII.15) можно переписать в следующем виде:

Л (е—у)

со8

в' 81

б'

а'в'

ах'=о

Л (8 — у)созХ'8Ш0'зт0'й0'

с1\'

= 0 (VIII.17)

<о

Л (8 — У)

81П Я,' 81П

81П

6' й%' = 0

О)

Из (VIII.17) следует, что аномалии силы тяжести не могут быть заданы

на сфере произвольно. Если условия (VIII.17) не соблюдаются, то это свиде-

тельствует о наличии ошибок в измерениях аномалий.

Искомая гармоническая функция в соответствии с (VI.4) определяется

рядом

оо с»

Г(Р, е, = =

(УПШ)

п-0 п=О

где У

(6, X) неизвестная гармоническая функция. Требуется определить не-

известные функции У

(0, X) через известные §

(0, X), заданные на сфере.

Указанную задачу можно решить, используя граничное условие (УШ.Ю).

Продифференцируем функцию Т (VIII.18) по р и сложим полученное значение

с величиной 2Т/р. Затем получим предельное значение этой суммы при р Н

190'

в виде бесконечного ряда сферических функций У"„ (О, А,). Полученный ряд,

= также ряд (VIII.12) подставим в граничное условие (УШЛО). Получим

дТ

„

7»= О

со

2Г

2 у

«(

рЛ+2

71=0

Предельное значение суммы 2Т/р + дТ/др при р й будет

дТ . гт I Я)

др Р 1р->-В

УП (0. Я)

71=0 71=0

Следовательно, граничное условие можно представить

СО

В соответствии с теоремой о единственности разложения функции, заданной на

сфере, в ряд по сферическим функциям два таких ряда могут быть равны лишь

при условии, если коэффициенты при соответствующих сферических функциях

равны.

Приравнивая сферические функции одинаковых степеней, будем иметь

-*«(в, Я). (VIII.19)

Отсюда следует вывод, что сферическая функция первой степени в раз-

ложении аномалии силы тяжести в ряд (0, Я) должна равняться нулю. Дей-

ствительно, (VIII.19) при п ~ 1 дает

й(в, Ь) = 0. (VIII.20)

Следовательно, величину У

(0, X) нельзя определить по аномалиям силы

тяжести. Все остальные сферические функции определяются в виде

(0,

ВпФ

к)

. (VIII.21)

Это соотношение связывает коэффициенты разложения возмущающего

потенциала с коэффициентами разложения аномалии силы тяжести.

Подставив полученные значения функции У

(0, X) всех степеней, кроме

первой, в ряд (VIII.18), получим

(Р.

в, = + №-22)

П=0

191'

Выделим сферическую функцию нулевой степени

Г(Р, 0, *.) = -

дя

Х)

+ +в ,

(

уш.23

п~ 2

полученный ряд при р = В называется рядом Стокса.

Сравнивая (VIII.23) с (У1.4), получим

-7?^

(б,

Я)

= /(М-М

), (VIII.24'

подставив значение §

(0, К) из (VIII.14), найдем

/ (М —М

) = 2В (Ж

)

- ДО (

ём

- у

) Ло. (VIII.25)

О)

Это равенство при известной разности Ш

— 17

можно использовать для

определения массы Земли. Учитывая приведенные выше соотношения, пере-

пишем обобщенный ряд Стокса в виде

Т(р, 0, я)=р2Я(Ж

-г/о)—

со

2(тГ-^г-

(УП1

71=2

Если р = В, для возмущающего потенциала на поверхности сферы получим

со

Ух

(9. Л) , р\/

п= 2

(VIII.27)

Таким образом, решение краевой задачи получено в виде бесконечного

ряда. Ряд этот сходится медленно. Для определения возмущающего потенциала

Стоксом также получена интегральная формула, вывод которой приводится

в следующем параграфе.

Учитывая соотношения (VIII.11), (VIII.20) и (VIII.14), разложение

(VIII.

12)

можно представить в виде

0г-Т) = (г-Т)ср + 2*п(е, Ц, (VIII.28)

11=2

где в соответствии с (VIII.13) и (VIII.16)

Вп (0, X) = Ц (8-у) Рп (созЧ>) йсо. (У1Н.29)

со

Итак, в разложении аномалии силы тяжести в ряд (VIII.28) по сферическим

функциям не должно содержаться членов первой степени, а при соответству-

ющем выборе нормального потенциала не будет членов и нулевой степени.

192'

В этом случае разложение аномалии в ряд будет начинаться с членов второй

степени

со

От-г) = 2 Впф, Я

п-2

§ 44. ОПРЕДЕЛЕНИЕ ВОЗМУЩАЮЩЕГО ПОТЕНЦИАЛА

НА ПОВЕРХНОСТИ СФЕРЫ (РЕШЕНИЕ СТОКСА)

Представим ряд Стокса (VIII.26) в виде

г<р, в, м =

СО

со

п= 2 со

Заменив в последнем интеграле его значением из (VIII. 11), получим

гв,. е,

ОО

2(тГ-2г'-«-«г-

(УШ

30)

со "-п=2

Во втором и четвертом членах правой части равенства (VIII.30) под знаком

интеграла стоит смешанная аномалия в свободном воздухе. Введем обозначение

п=2

п получим так называемую обобщенную функцию Стокса. Просуммируем ряд

(VIII.31).

Обозначив В/р = х, ряд (111.18) представим в виде

оо

2 х

(соз

г|7).

1^1+3:2 —

23;

со вя|) Р

Отсюда

==- = У Х

(соз

1|5).

У 1+ж2

— 2ЖС08 1|)

п=о

пли

УТ — 2х со5

г|)

Л — X соз

= 2

(соз яр).

(УП1.32)

п=2

Умножим обе части этого равенства на йх/х

и проинтегрируем в пределах

от х -> 0 до х

оо

I [угтй^ -

- ^=(

со8

П=2

13 Заказ 1379 193

интеграл в левой части этого равенства представим суммой трех интеграл:

X X

X XX

Г 1 Ах ? йх Р С08я])йж

/1 + ж2_2гсозг|з

Первый интеграл вычисляется при помощи подстановки х = 1/у. Отеке

Г 1 Ах _ Г уАу

3 + 2хсо8г|э

ж2

] /ц-у2_2ус08г|) *

Последний интеграл является табличным. Известно, что

Г уАу __ УауЪ+Ьу+с Ь Г Ау (VIII 3"

3 Уау2+Ьу+с а 2а ] у

ау

+ Ьу + с

' К • "

(причем а > 0)

В нашем случае а — 1; Ь = —2 сое яр, с = 1. Поэтому

СОЗ 1)51п

(1/1 -\-у

—

2у

СОЗ

—

С08 Яр)].

После перехода к переменной х окончательно получим

Г - = -[/!+ 1-^^ + 003^ /1+1200^

]

л;21^1

+ ж

—2х

соз г|>

I. У < х* х * у ~г

х2 х

-\--

—соз ф^ = — ^ 1/1 +х

— 2х

соз яр

+ соз

яр 1п

(1/1 -(-ж

—

2ж

соз

яр 1

— х

соз

г]))^.

В свою очередь

Г Ах 1 Г созФйг . ,

)-±Г = -Т> ) 3

=008115

1п X.

Таким образом,

со

П-1 С \ г

г Р

(созяр) = ]—— созяр1па: у 14- х

—

2а;

соз

яр

—

— 1

I ^

П=2

—

СОЗ Яр

1п ^1+^

-2з:соз^ + 1-а:со8Т|;|

194'

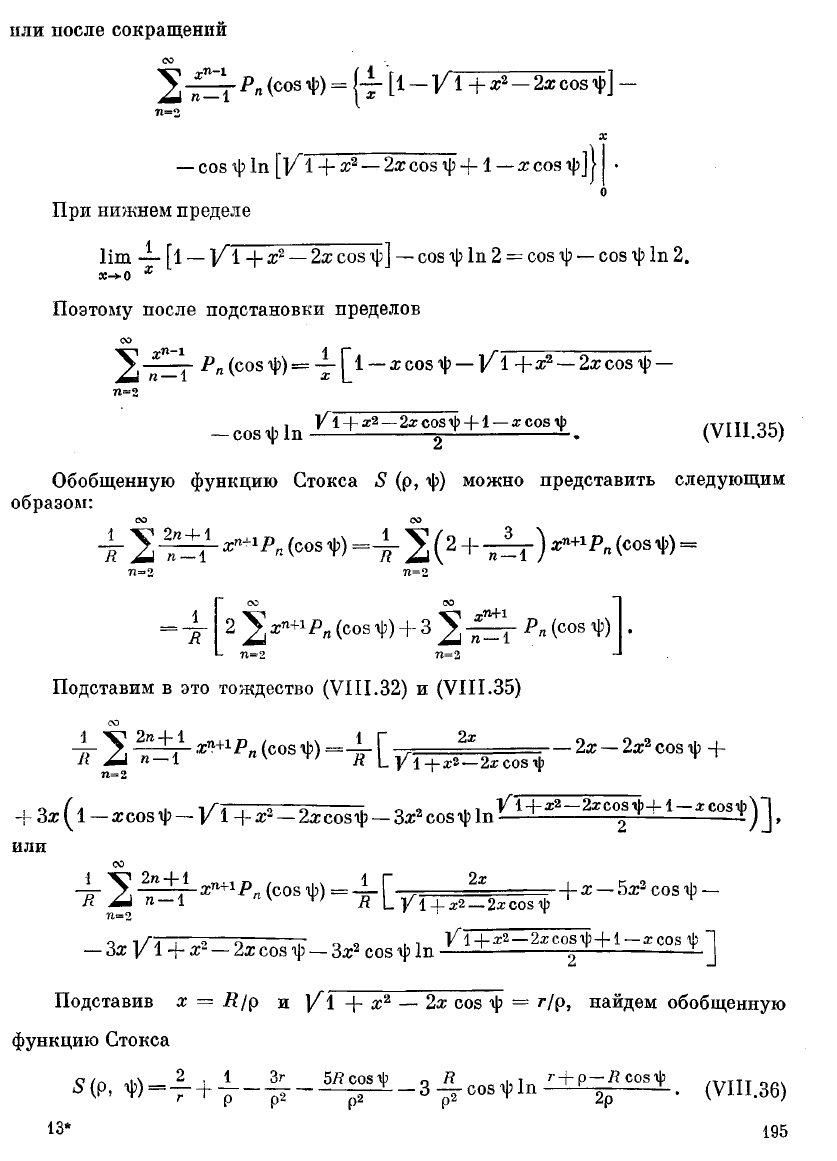
пли после сокращений

со

2т=Г

С08=

-2^005^] -

п=2

— соз

\|> 1п

[VI + х

— 2х

соз г|?

— х

соя 1|>]|

•

При нижнем пределе

1пп — [1 —1/4 + х

— 2х соз

г|?]

—

соз г|>1п

2 = соз

-ф

— соз

1|з 1п

«->•0

Поэтому после подстановки пределов

(соза|))

= -^[1 —жсоз!|5 —1/1 +х

— 2x00311) —

71=2

, .

У\.-\-хЪ—2гсо5оЬ

+ 1—хсозгЬ

—

сое

1п

(VIII.35)

Обобщенную функцию Стокса 5 (р, т|)) можно представить следующим

образом:

1Г 2 1П=Г

хМР

" <

со8

=4" 2 (

ХП+1Р

»<

со8 =

_1_

05 ^

2 ^ *

п+х

Рп (соз

1>)

+ 3 2 Рп (соз ф)

71=2

Подставим в это тождество (VIII.32) и (VIII.35)

2х

У \-\-х%—2х

С08Я|)

- 2х — 23?

СОЗ 1)5

+ 3^(1-^003^-1/1+^-2x003^-3^ соз^1п

/1+д2

2з:со

8,|,+ 1

а:со

^)]

или

2х

—

5х

соз

"ф

—

У1 +

— соз г|)

п„лГл I „•> г о , У1 — 2х соз

1|)

+1 — х соз г})

— Зх у 1 + х- — 2хсоз

г|)

—

Зж

соз 1п —

—

Подставив х = К/р и + х

— 2х соз

я|з

= г/р, найдем обобщенную

функцию Стокса

5(Р.

{уииб)

13*

195

Подставив полученное значение 5 (р, -ф) в (VIII.30), получим

Г(р, е, + |

№-у)[8<р, (У1П.ЗГ

Отсюда можно получить значение потенциала на поверхности сферь^.

положив в этой формуле р = В.

В этом случае г = 2В зт г|)/2 и

8(В, = Ц^--6зт-|-+1-5со8'ф-Зсозя|)1п(8т^--!-8т

-|-)" .

(УНШ

или, обозначив выражение в квадратных скобках через 8 (г|з),

8 (В, ^ =

Следовательно,

Т(В, 0, = + (УШ.ЗР

со

Функция

©э

п=2

называется функцией Стокса.

Мы получили интегральную формулу Стокса.

Если бы Земля была сферой, то формула Стокса точно определяла бы воз-

мущающий потенциал Земли. Но в силу отличия Земли от сферы, применение

формулы Стокса при определении возмущающего потенциала Земли приводит

к ошибочным результатам.

Вопрос о том, каковы будут эти ошибки по величине явился предметом

большой дискуссии.

Казалось очевидным, что поскольку Стоке в качестве поверхности интег-

рирования использовал сферу, а не эллипсоид (а отступления сферы от эллипсо-

ида являются величинами первого порядка малости), то и ошибки вычисления

возмущающего потенциала Земли — Т по формуле Стокса будут того же

порядка.

Однако в 1913 г. итальянский ученый Пицетти доказал, что ошибки, воз-

никающие при применении формулы Стокса будут иметь порядок Та. Поскольку

возмущающий потенциал Земли Т является величиной второго порядка малости,

а сжатие Земли а — первого порядка, то величина Та будет иметь третий поря-

док малости. Последующие исследования подтвердили вывод Пицетти.

Формулу Стокса (VIII.39) следует рассматривать, как приближенно опре-

деляющую возмущающий потенциал Земли.

Рассмотрим еще один возможный способ определения возмущающего

потенциала Земли.

Представим возмущающий потенциал во внешнем пространстве Т в виде

потенциала простого слоя плотности ц, распределенного на поверхности сферы о,

т. е.

(УШ.40)

196'

Тогда задача определения потенциала Т сведется к определению неизве-

стной плотности

В соответствии с (1.85) имеем

дТ

др

— —

С С

(ХС08(

;°-

р)

ав - 2яц (9, Я). (VIII.41)

р->"Н ^ г

Поскольку на сфере

соз(г

р) = -^-,

то

= Ч (VIII.42)

дТ

др

р^п

Подставим (VIII.40) и (VIII.42) в краевое условие (VIII.10)

после суммирования получим интегральное уравнение для определения плот-

ности и (0Д)

2Я|4

(0, = + (У1П.43)

Заменим плотность [х (0', К'), стоящую под интегралом, через величины,

заданные на сфере.

Прежде всего заметим, что интеграл

^ а»

а г о г

сг ю

равен значению потенциала Т (VIII.40) на сфере (р = В). Он уже определен через

смешанные аномалии, заданные на сфере (VIII.39)

Т (В, 6,

Я)

= Д

<&»

= 2

(ТГ„

-11

) +

Х)

(О

жли, учитывая (VIII.11)

Е2

а<й

=И

<*>

~ « + ' (

УШ

(О 6>

Подставив значение потенциала Т (В, 0, X) в (VIII.43) получим решение

интегрального уравнения в виде

Ив,

ь>

НЛП

ие, = ^ + + (*>-№. (VII 1.45)

(4я)2

(я

197'

С интегралами этого вида нам придется встречаться неоднократно; в нг

под знаком интеграла всегда стоит произведение двух функций. Первая —

в данном случае 8$

— есть некоторая непрерывная функция, заданная во вс<

точках сферы соответственно условиям данной конкретной задачи, она назг

вается обкладкой; второй множитель — в данном случае 5 (ф) — зависг

лишь от координат элемента йоа и координат 0 и X, называется он ядром инте:

рала.

Итак, формула Стокса (VIII.39) полностью решает поставленную проблему

т. е. определяет возмущающий потенциал Земли для случая, когда краев-:

условие (VIII.

10)

отнесено к сфере. Полученное решение справедливо липг-

в случае, если на сфере соблюдается условие

^8#

СО8яМ<О = 0, (УШ.4»

или иначе, справедливы соотношения (VIII.15).

Условие (VIII.46), или соответствующие ему (VIII.15), называется уел с

вием существования полученного решения.

Единственность решения обеспечивается в случае, если будут выполняться

определенные требования к нормальному потенциалу Земли. Остановимся н.

этом вопросе.

Перепишем формулу Стокса (VIII.39), выделив особо сферические функции

нулевой и первой степени

т(Н, е, +

«в

Для сферической функции первой степени находим

ф, X) = /М (г

сов 6 + сов X

81П

6 + г/

зт X вш 0), (VIII. 45

где х

, г/

, г

— координаты центра массы Земли.

Таким образом, возмущающий потенциал Земли определяется не тольк.:

аномалиями силы тяжести (§ — 7), но и зависит от постоянных величин

«о. У01

значения которых находятся в прямой зависимости от способа определения

нормального потенциала.

Так, в частном случае при определении нормального потенциала можно

поставить следующие условия.

1. Масса выбранного эллипсоида М

должна равняться массе Земли М.

что в соответствии с (VIII.25) тождественно требованию, чтобы сферическая

функция нулевой степени в (VIII.47) равнялась бы нулю

2 (ТР

- сд —ЭД (8 - у)

йсо

= 0. (VIII.49)

198'

2. Потенциал II

на поверхности эллипсоида должен равняться потен-

циалу И^о в начальной точке, т. е.

И'о-С/о-О,

и. следовательно, на основании (VIII.49) должно удовлетворяться условие

§§ (е-7)<Ьо = 0. ' (VIII.50)

3. Центры масс эллипсоида и Земли должны совпадать, т. е.

Хо

Уо

о = °- (VIII.51)

Поставленным требованиям удовлетворяет общий земной эллипсоид.

Таким образом, для общего земного эллипсоида формула Стокса при-

нимает более простой вид

Т(Н, 6, (VIII.52)

Если бы масса Земли М и значение потенциала в начальной точке

были известны, то большая полуось общего земного эллипсоида а и величина у

определялись бы из формул (У.26) и (У.27). Однако ни М, ни \У

с надлежащей

точностью неизвестны и для определения размеров общего земного эллипсоида

к элементов его ориентирования используют астрономо-геодезические и спут-

никовые методы (см. § 77).

§ 45. ФОРМУЛА СТОКСА ДЛЯ ВЫЧИСЛЕНИЯ ВЫСОТЫ

КВАЗИГЕОИДА И ФОРМУЛЫ ВЕНИНГ-МЕЙНЕСА

ДЛЯ СОСТАВЛЯЮЩИХ УКЛОНЕНИЯ ОТВЕСА ОТНОСИТЕЛЬНО

ОБЩЕГО ЗЕМНОГО ЭЛЛИПСОИДА

Используя соотношения (VI.19) и (VI.8) между возмущающим потен-

пвалом и элементами, характеризующими фигуру Земли, можно определить

гысоту квазигеоида ^ и составляющие уклонения отвеса \ и г). Так, на основа-

няп (VI.19) можно с учетом (VIII.52) получить

ТгК называемую формулу Стокса для высоты квазигеоида относительно общего

земного эллипсоида.

Для вычисления составляющих отвеса используем соотношения (VI.8),

5 которых положим р = В. Дифференцируя формулу Стокса (VIII.52) по пере-

*-гнным В и Ь, получим

(А

(О

199'