Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

Задача сводится к решению обыкновенного дифференциального

уравнения (14.109) при соблюдении граничных условий (14.110) и

(14.111).

Дифференциальное уравнение (14.109) совпадает с модифици

рованным дифференциальным уравнением Бесселя (П. 124), а

потому его решение выражается с помощью модифицированных

функций Бесселя нулевого порядка I и II рода — см. (П. 125):

A P (r ,s )= A lJ ^ r )+ B K 0( ^ r \

(14.112)

где А и В — постоянные и пока неизвестные величины.

Согласно известному свойству модифицированной функции

Бесселя/о f v r г I , ее величина неограниченно возрастает с ростом

^ / г 1

аргумента, т.е. / 0 v к г - » 00 при Поэтому, чтобы удов

летворить условию на бесконечности (14.111), в уравнении (14.112)

надо принять, что

А = 0. (14.113)

Подставив в уравнение (14.112) условие (14.110), определим

коэффициент В:

_ _ _ _ _ _ _ _ _

АР су

Г Ж у <14Л14>

sKo^ V k K cJ

Учитывая равенства (14.112)—(14.114), получим:

АР (r,s) = Ap

(14.115)

Для перехода от изображения АР (г, s), определяемого равен

ством (14.115), к оригиналу Ap(r,t), Ван Эвердинген и Херст [972]

использовали формулу обращения Мелина и в итоге нашли, что

2 Т и -е" )Y0(ur)-Y0(u )J0(ur)]

»<'•*> =

----------

■B>[/g(«) + Kj(«)J ~ dU-

(14.116)

Расход жидкости Q ( л О в момент / через боковую поверхность

цилиндра радиуса г, коаксиального скважине, определяется по

формуле Дюпюи так:

С (Л »>~2 <14117>

^ v |i dr

Количество (объем) жидкости V ( г, f ), которое до момента *

пройдет через боковую поверхность того же цилиндра, должно

быть равно

* k Я *

V(r,t) = [Q(r,t)dt = -2nrb--^jAp(r,t)dt. (14.118)

О ^ О

Подвергнем уравнение (14.118) преобразованию Лапласа:

V(r,s) = - 2 n r b - ~ L

№

Эг

jAp(r,t)dt

(14.119)

где V ( г, s ) — изображение функции V(r%t\L — символ преобра

зования Лапласа.

Из операционного исчисления известно, что если оригинал

подвергается интегрированию, то изображение оригинала должно

быть разделено на параметр Лапласа s. Изображение А Р ( г, s )

функции Ар ( г, О уже было найдено; оно определяется равенством

(14.115); разделив это изображение на s, подставим результат в

формулу (14.119):

я. . . к Э ApcyKol V k"г j

У(Г-Й}Ш- М > * 7 Ц ^

Выполняя дифференцирование модифицированной функции

Бесселя К с

согласно соотношению (П. 166), получим

iГг, Ч о __ь*АРсу ^ llV iT r

V(r,s) = 2nrb у -

V k * c

(14.121)

Чтобы перейти от изображения V(r,s), определяемого равен

ством (14.121), к оригиналу V(r,t), причем для случая, когда

г - Rc, Ван Эвердинген и Херст [972] вновь использовали формулу

обращения Мелина и нашли

3 Kt

V ( R c, t ) = V c ( t ) = * R 2 c b k h P c y I д р 2 6

Ju3[/g(u) + K§(u)] ’(14

12 2)

где V c(t) — объем накопленной скважиной добычи жидкости за

время f.

Интеграл, входящий в правую часть последней формулы, Ван

Эвердинген и Херст подсчитывали численным методом и в

цитированной выше статье составили подробную таблицу для

безразмерной величины Vn выражаемой таким равенством в

функции безразмерного параметра Фурье /0:

VciU)-

du,

(14.123)

где/о определяется соотношением (14.27).

Для использования ценной таблицы Ван Эвердингена и Херста

надо учитывать такую связь между размерной и безразмерной

величинами V c и Vc, которые выражаются с помощью равенств

(14.122) и (14.123):

V c = 2nRH

Vc = 2KR2cb$*APcyVc,

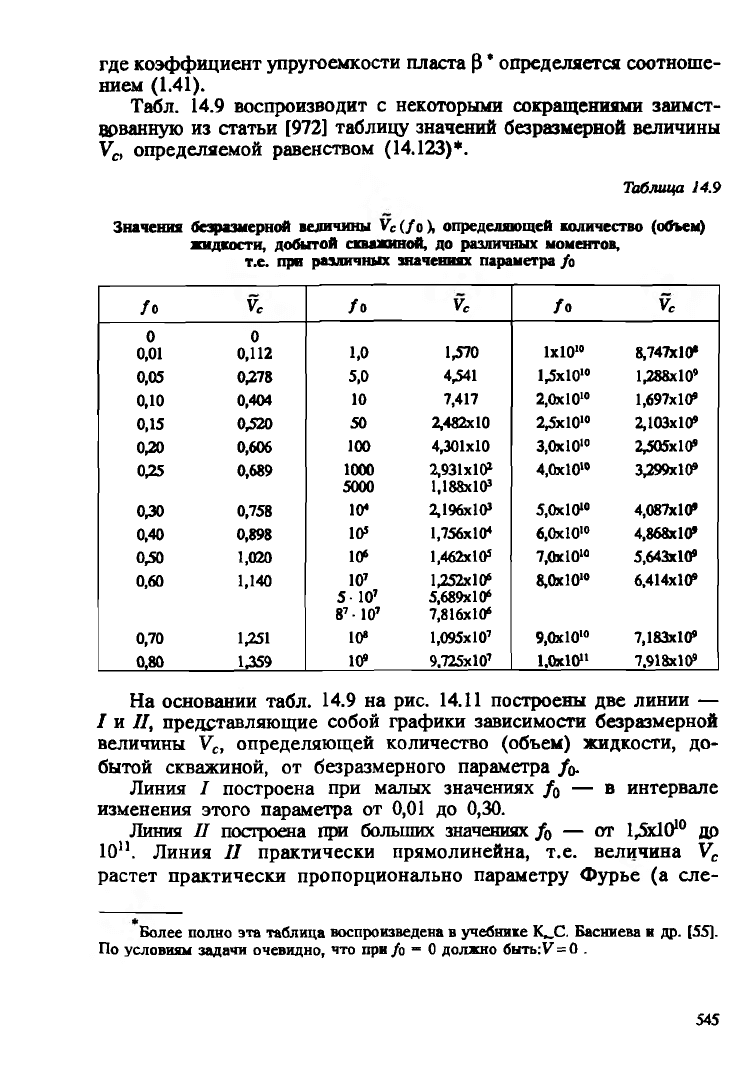
где коэффициент упругоемкости пласта Р * определяется соотноше

нием (1.41).

Табл. 14.9 воспроизводит с некоторыми сокращениями заимст-

врванную из статьи [972] таблицу значений безразмерной величины

Vct определяемой равенством (14.123)*.

Таблица 14.9

Значения безразмерной величины Vc (/о X определяющей количество (объем)

жидкости, добытой скважиной, до различных моментов,

т.е. при различных значениях параметра /о

/о

Vc /о Vc

/о

0 0

0,01

0,112 1,0

1,570

1х1010

8,747x10*

0,05

0,278

5,0

4Г541

UxlO10

1,288x10»

0,10

0,404

7,417

2,0x1010 1.697Х109

0,15

0,520

2,482x10 2^х1010 2,103x10®

0,20 0,606

100

4,301x10 3,0x1010 2Д05х10»

0,25 0,689

1000

2,931x10* 4,0х101в

3^99x10»

5000

1,188x10s

0,30 0,758

104

2,196x10*

5,0x10*° 4,087x10*

0,40 0,898

105

1,756x1с4 6,0хЮ10 4,868x10*

0,50

1,020

106

1,462x10* 7,0x1010 5,643x10»

0,60 1,140

107

1,252x106

8,0х1010 6,414x10»

5- 107

5,689x10е

87 ■ 107

7,816x10е

0,70 1,251

10*

1,095х107 9,0х1010 7,183x10»

0,80 1359

10е 9,725х107

1,0x10й 7,918x10»

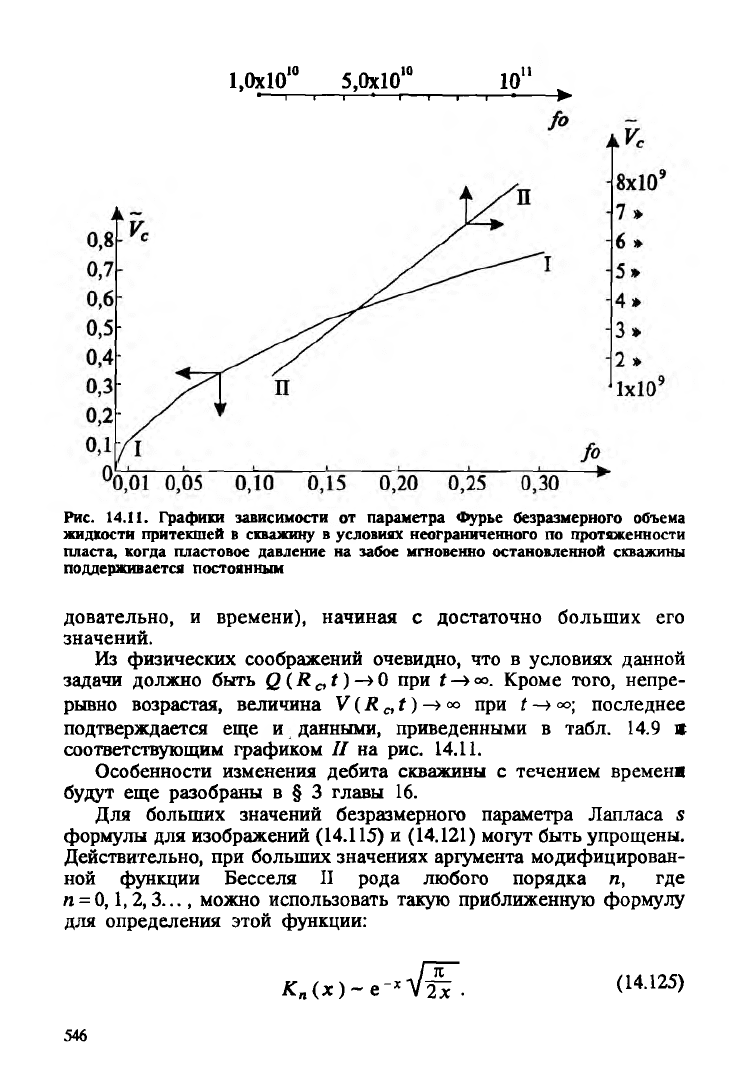
На основании табл. 14.9 на рис. 14.11 построены две линии —

/ и //, представляющие собой графики зависимости безразмерной

величины VCJ определяющей количество (объем) жидкости, до

бытой скважиной, от безразмерного параметра /о.

Линия / построена при малых значениях /0 — в интервале

изменения этого параметра от 0,01 до 0,30.

Линия II построена при больших значениях /0 — от 1,5x10ю др

1011. Линия II практически прямолинейна, т.е. величина Vc

растет практически пропорционально параметру Фурье (а сле-

Более полно эта таблица воспроизведена в учебнике К_С. Басниева и др. [55].

По условиям задачи очевидно, что при /о = 0 должно быть:У = 0 .

1,0x10*° 5,0x10’° 10п ^

----

•

----

------

►

Рис. 14.11. Графики зависимости от параметра Фурье безразмерного объема

жидкости притекшей в скважину в условиях неограниченного по протяженности

пласта, когда пластовое давление на забое мгновенно остановленной скважины

поддерживается постоянным

довательно, и времени), начиная с достаточно больших его

значений.

Из физических соображений очевидно, что в условиях данной

задачи должно быть Q (R at)-*0 при £—><». Кроме того, непре

рывно возрастая, величина V (R cyt)->c° при t —> <*>; последнее

подтверждается еще и данными, приведенными в табл. 14.9 ш

соответствующим графиком II на рис. 14.11.

Особенности изменения дебита скважины с течением времени

будут еще разобраны в § 3 главы 16.

Для больших значений безразмерного параметра Лапласа s

формулы для изображений (14.115) и (14.121) могут быть упрощены.

Действительно, при больших значениях аргумента модифицирован

ной функции Бесселя II рода любого порядка тг, где

/1 = 0,1,2,3..., можно использовать такую приближенную формулу

для определения этой функции:

На основании соотношения (14.125) вместо равенств (14.115) и

(14.121) получаются такие приближенные формулы для изобра

жений:

V(r,s)~2itrb

A P(r,s)~ i

(14.127)

(14.126)

Здесь необходимо сделать оговорку: вывод только что пол

ученных приближенных формул был сделан в предположении, что

достаточно велики величины аргументов модифицированных фун

кций Бесселя, входивших в формулы (14.115) и (14.121). Следова

тельно, надо считать, что достаточно большую величину имеет не

гр Лапласа s, но что велики величины произведений

Полученные приближенные выражения для изображений столь

просты, что позволяют легко найти по ним оригиналы функций.

Именно, используя типовые формулы перехода от изображений к

оригиналам — см., например, формулы № 50 и № 52 на стр. 585

[427] или формулу № 11 на стр. 483 [350], получим

Учитывая сделанную выше оговорку о возможности использо

вания приближенных формул (14.126) и (14.127), следует помнить,

что и приближенными формулами (14.128), (14.129) можно пользо

ваться при столь малых значениях времени t9 что и величины

к t K t

— 2 оказываются достаточно малыми.

v г у 2Vk7 ’ (14.128)

Положим г - Rg в двух последних формулах и учтем соотно

шения (П. 24) и (П. 35):

Ар (R at)~ Ар ру = const, (14.129а)

v ( * „ n . v , < o - i ^ p £ * V F . <М130>

Равенство (14.129а) подтверждает постоянство понижения дав

ления на стенке скважины (на контуре С), что соответствует

принятому в задаче граничному условию (14.4).

Формула (14.130), определяющая для малых значений времени

t объем добытой жидкости из скважины, совпадает с аналогичной

формулой для одностороннего прямолинейно-параллельного при

тока жидкости к прямолинейной галерее из полубесконечного

пласта Действительно, при одностороннем притоке жидкости к

прямолинейной галерее объем добытой из нее жидкости Vс (t) за

время t может быть определен по формуле (4.145а), которую, с

учетом сделанного к ней примечания, перепишем так:

ve(t) =

2 ok Ар

У5Гц7к

(14.131)

Примем, что длина участка прямолинейной галереи равна

периметру окружности кругового сечения стенки скважины радиуса^;

тогда площадь о стенки рассматриваемого участка прямолинейной

галереи определится так:

o = 2nRcb. (14.132)

Подставим величину о из равенства (14.132) в (14.131):

|x Vk

V c(t) = 4 'l* Rcbr * P cyJ i. (14ЛЗЗ)

Итак, формула (14.133) совпала с приближенной формулой,

т.е., действительно, при малых значениях времени приток

жидкости к скважине конечного радиуса происходит по такому же

закону как и к прямолинейной галерее.

Проверим степень погрешности формулы (14.130). Для этого

несколько преобразуем правую ее часть, учитывая соотношения

(1.41) и (14.27):

<14Л34)

Сравнивая правые части равенств (14.134) и (14.124), определим

используемую Ван Эвердингеном и Херстом [972] безразмерную

величину VCi которой можно пользоваться при малых

значениях /0:

^ - £ ^ « 1 , 1 2 8 ^ . <14Л35>

Бели обе части равенства (14.135) продифференцировать по

d V

параметру/о, то легко убедиться в том, что .. с = « при / о = 0,

“ / о _

т.е. кривая линия, соответствующая графику зависимости Vc от /0

касается оси ординат в начале координат, что отражено на

рис. 14.11. Начальный участок графика, судя по равенству (14.135),

представляет собой параболу. Полезно сопоставить похожие формы

таких же графиков на рис. 13.7а и 13.15.

Полагая в равенстве (14.135) /о ■ 0,01, получим, округляя

результат до трех значащих цифр, что

Vc ~ 0,113. (14.136)

Это найденное по приближенной формуле (14.135) значение

величины Vc отличается менее чем на 1% от приведенного в

табл. 14.9 значения 0,112 при той же величине/0.

При /о ” 0,5 погрешность подсчета по приближенной формуле

(14.135) составляет уже около 10%.

Ван Эвердинген и Херст сами оговорили, что они составили

свою табл. 14.9, начиная со значения/0 - 0,01 именно потому, что

при меньших значениях /0 можно обойтись без таблицы, используя

для подсчетов величины Vc с высокой степенью точности простую

приближенную формулу (14.135).

В § 3 главы 16 приводится табл. 16.8, которая существенно

дополняет табл. 14.9 тем, что в ней приведены итоги подсчета

изменяющегося со временем безразмерного дебита скважины,

пущенной при тех же условиях, какие были рассмотрены в данном

параграфе.

§ 7. Задание постоянного дебита скважины

в пласте бесконечной протяженности

Предполагается, что в начальный момент в бесконечном пласте

скважина конечного радиуса Rc пущена в эксплуатацию с посто

янным дебитом Qcу.

Следовательно, рассматриваемая задача, как и та, которая была

решена в предыдущем параграфе, так же относится к сформули

рованной в начале § 1 данной главы задаче III типа.

Задание конечного радиуса скважины делает задачу опять

неавтомодельной. Отличие рассматриваемой здесь задачи от той,

которая была решена в предыдущем параграфе, состоит только в

различии граничного условия на стенке скважины: в § 6 задавалось

постоянное понижение давления, а здесь задается постоянный

дебит, а следовательно, задается постоянная величина градиента

понижения давления на стенке скважины.

Итак, математическая постановка задачи такова: требуется

определить понижение давления Л р ( г, t ) в любой момент в любой

точке бесконечного пласта при соблюдении начального условия

(14.3), условия на бесконечности (14.108) и еще такого граничного

условия (на окружности С радиуса Rc) — см. рис. 14.1:

~ — 2nRcb

Э А р ^

дг

r = R c = Q c у = const.

(14.137)

при t>0.

При этих краевых условиях надо проинтегрировать дифферен

циальное уравнение пьезопроводности (14.1).

Будем решать задачу операционным методом. Подвергая пре

образованию Лапласа уравнение (14.1), учитывая начальное условие

(14.3), подвергая преобразованию равенства (14.137) и (14.108),

отражающие граничные условия, и обозначая через А Р ( г, s)

изображение понижения давления, получим:

d2AP 1 dAP 1

dr2 + г dr к ’ (14.138)

к. _ ,/ЭД/О Qcjr (14.139)

-~2%Rcb g ,

AP = 0 при Г = оо. (14.140)

Как уже было отмечено в предыдущем параграфе, общее

решение обыкновенного дифференциального уравнения (14.138)

должно быть таково:

A P(rts)=AI0 ( Щ +вк0 [ Щ

(14.141)

Чтобы удовлетворить на бесконечности условию (14.140), надо

положить А = 0, т.к. значение функции /0 стремится к бесконеч

ности.

Итак, считая А = 0 и подставив величину А Р из равенства

(14.141) в граничное условие 14.139, определим коэффициент В:

QcуЦУк

________

_______

[ t e y

В ~ткськ [ Л/5 D 1

(14.142)

Подставив найденное значение коэффициента В в равенство

(14.141), получаем такое выражение для изображения A P(r,s):

Для перехода к оригиналу Ар (г, t) от изображения, представ

ленного равенством (14.143), Ван Эвердинген и Херст [972]

использовали формулу обращения Мелина и получили