Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1
Подождите немного. Документ загружается.

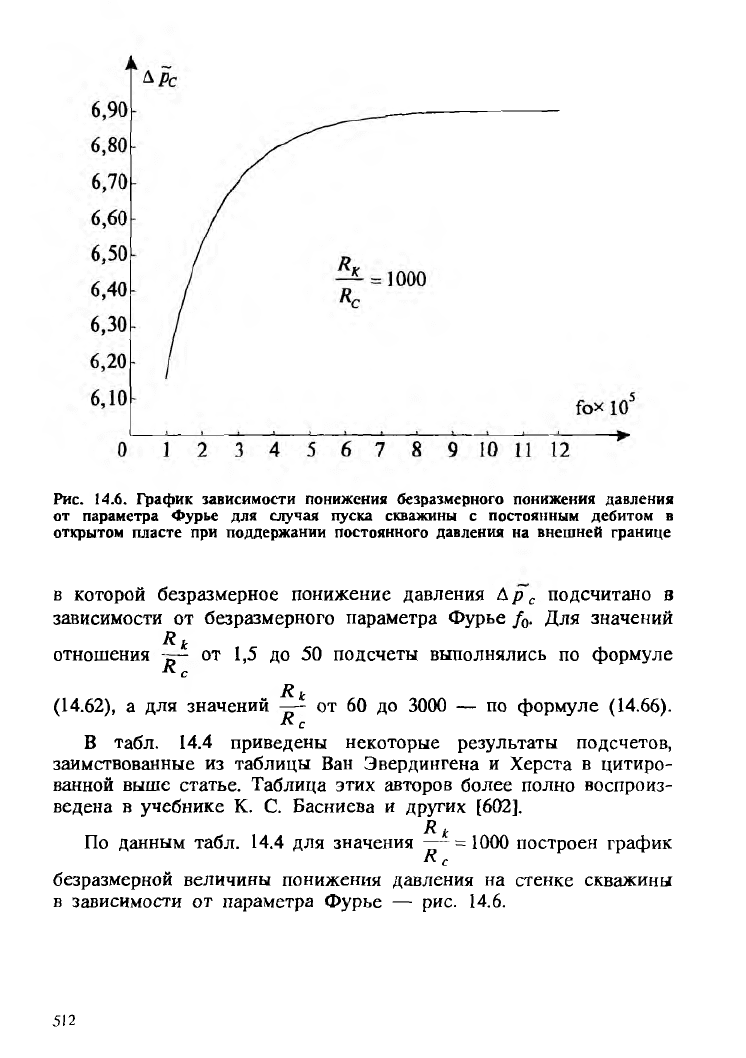
Рис. 14.6. График зависимости понижения безразмерного понижения давления
от параметра Фурье для случая пуска скважины с постоянным дебитом в
открытом пласте при поддержании постоянного давления на внешней границе
в которой безразмерное понижение давления А р с подсчитано в
зависимости от безразмерного параметра Фурье / 0. Для значений
Rk
отношения -д- от 1,5 до 50 подсчеты выполнялись по формуле
R с
Rk
(14.62), а для значений — от 60 до 3000 — по формуле (14.66).
R с
В табл. 14.4 приведены некоторые результаты подсчетов,
заимствованные из таблицы Ван Эвердингена и Херста в цитиро
ванной выше статье. Таблица этих авторов более полно воспроиз
ведена в учебнике К. С. Басниева и других [602].
Rk
По данным табл. 14.4 для значения — = 1000 построен график
R с
безразмерной величины понижения давления на стенке скважины
в зависимости от параметра Фурье — рис. 14.6.
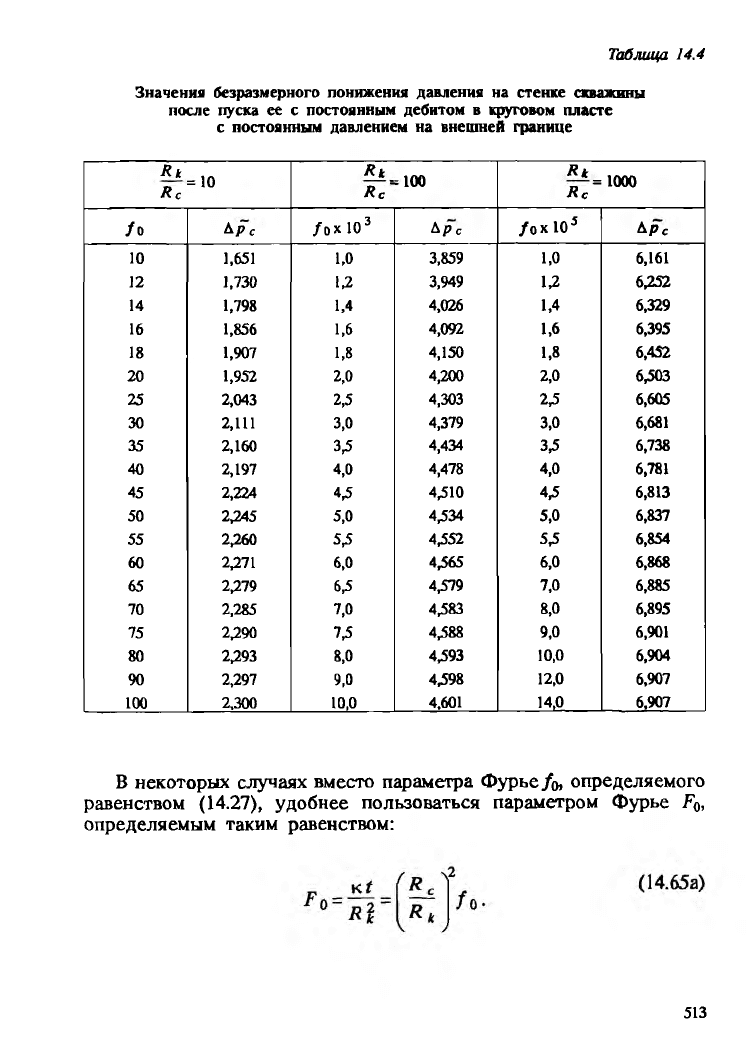
Значения безразмерного понижения давления на стенке скважины
после пуска ее с постоянным дебитом в круговом пласте
с постоянным давлением на внешней границе
Rk
R с
= 10
Rk
Rc'
= 100
Rk =
Rc
1000
/о
А рс
/о х Ю 3
А Рс
/о х 10 5
А рс
10
1,651
1,0
3,859
1,0 6,161
12
1,730
1,2
3,949
1,2
6,252
14
1,798
1,4
4,026
1,4
6,329
16
1,856
1,6
4,092
1,6
6,395
18
1,907
1,8
4,150
1,8
6,452
20 1,952
2,0
4,200
2,0
6,503
25
2,043
2,5
4,303
2,5 6,605
30
2,111
3,0
4,379
3,0
6,681
35
2,160
3,5
4,434
3,5 6,738
40
2,197
4,0
4,478
4,0
6,781
45 2,224
4,5
4,510 4,5
6,813
50
2,245
5,0
4,534 5,0
6,837
55 2,260
5,5
4,552 5,5
6,854
60
2,271
6,0
4,565 6,0
6,868
65 2,279
6,5
4,579 7,0
6,885
70 2,285 7,0
4,583
8,0
6,895
75
2,290
7,5
4,588
9,0
6,901
80
2,293
8,0
4,593
10,0
6,904
90
2,297
9,0
4,598 12,0 6,907
100
2,300
10,0
4,601
14,0
6,907
В некоторых случаях вместо параметра Фурье /о, определяемого
равенством (14.27), удобнее пользоваться параметром Фурье F0l
определяемым таким равенством:

Соответственно вместо корней xv уравнения (14.65) используют
корни х у уравнения
JQ(XV' ) = 0,
(14.656)
где
(14.65в)
В новых обозначениях формулы (14.63), (14.66) прини
мают такой вид, который встречается во многих статьях и
монографиях:
Р ^ 0 v &
1 п ^ -2 У V ,
r ^7iX'U2i (xvr
л К t
(14.63а)
г, 00 / о X у
ДРс(^о) = 1 п ^ -2 Х - #} -^ е
с v= 1 v 1 ' v '
(14.66a)
Следует помнить, что и эти формулы справедливы только при
Rk » R с; они гарантируют высокую степень точности подсчетов
при Rk>50Rc.
При проведении подсчетов по формулам данного параграфа, в
частности по формулам (14.63а), (14.66а), значения функций Бесселя
и их нули можно брать, например, из сборников таблиц [551],
[781], [428]. Во II части таблиц [428] приведены значения функций
для первых 40 корней x v' уравнения (14.656) и для
, г
Я*
значений величины изменяющейся в пределах от 0,01 до 1.
Rk
Значения функций J{(xv') для первых 40 корней уравнения
(14.656) указаны на стр. 298 сборника таблиц [781].

§ 4. Задание постоянного давления на стенке скважины при
непроницаемой внешней границе пласта
Решаемая в данном параграфе задача отличается от той, которая
была исследована в § 2 только тем, что пласт на внешней круговой
границе К — см. рис. 14.1 — предполагается закрытым. Следова
тельно, не может быть притока жидкости в пласт через его
непроницаемую внешнюю границу, что создает в пласте условия
замкнуто-упругого режима.
Математически задача ставится так: требуется найти решение
дифференциального уравнения пьезопроводности (14.1) при вы
полнении начального условия (14.3), граничного условия (14.4) на
внутреннем контуре С (на стенке скважины) и еще такого
граничного условия на внешнем контуре К:
при г ,>0. <14-67>
О г
Общее решение дифференциального уравнения (14.1) может
быть представлено формулой (14.8). При учете граничного условия
(14.4) получаем формулу (9),
Продифференцируем по г равенство (14.8), используя при
дифференцировании бесселевых функций соотношения (П. 163) и
(П. 164):
Э Ар ( r,t) D\ _ 1 -
Эг
' 1 v
+ BV'Y х
2 К t
е Rc
(14.68)
Подставим г = Rk в последнее равенство и учтем граничное
условие (14.67):
о D1 1 V
0=Т к~Т с^ х '
* cv = l
A'ji
Rk
Rc
\+Bv'Y,
2 К t
e"XvRl
(14.69)
Для выполнения равенства (14.69) в любой момент необходимо,
чтобы

А у / j х v R
\
( Rk]
+BV'Y X
^Vn
Rc)
= 0,
£>1=0.
(14.70)
(14.71)
Так как левая часть равенства (14.9) не должна зависеть от
времени, то этому же условию должна удовлетворять и правая его
часть; следовательно, учитывая еще равенство (14.71), получим
Ay'J0(Xy)+Bv'Y0(Xy) = 0, (14.72)
D 2 = Ар с у . (14.73)
Исключим величины A v' и Ву' из равенств (14.70) и (14.72):
Я,
Y0(xv)-J0(xv)Yl
= 0.
(14.74)
Итак, величины xv должны быть корнями трансцендентного
уравнения (14.74).
Выразим из равенства (14.70) коэффициент Bv' через Av‘ и
подставим это выражение в формулу (14.8), учитывая соотношения
(14.71) и (14.73):
Ap(r,t) = Apcy + YtAy'x
R.
I
/v=1 N f
х ^
VR,
-J
Rt
R c
Y0
v-
VR.
(14.75)
2 Kt
Yо
Введем в рассмотрение функцию Ww являющуюся линейной
комбинацией бесселевых функций и отличающуюся от функции
Uv, использованной в двух предыдущих параграфах:

w v
Г '
( г л
Rk)
*
/ \
I т
XvT c \
о
II
XvT c I
У\
Х'Г С
-J 1
х'Т е \
Уо
XvT c
\ )
\ )
V J
\ )
< / /
Полагая г = Rc в равенстве (14.76), получаем, учтивая урав
нение (14.76),
Wv(xv)=J0(xv)Yl
Rk'
Rk)
XvT c \
V J
-J 1
Xvirc
V /
Yq(xv) 0, (14.77)
т.е. величины xv оказываются корнями функции Wv(xv).
С помощью функции Wv можно переписать формулу (14.75)
так:
Д>(Л/) = ДРсу + £ '
Ау | .. г
V = 'Y о
\ _ 2 к t
е х'*1.
(14.78)
В формуле (14.78) неизвестными остались только коэффици
енты Л у . Для их определения надо учесть неиспользованное пока
начальное условие (14.3). Именно, полагая t * 0 в формуле (14.78)
и учитывая условие (14.3), получим
д р * = - Г
AJ
v-i У,
Wv
(14.79)
Воспользуемся теперь таким известным разложением в ряд
постоянной величины по функциям W у
г
h
оо Jq (X у ) J 1
V
/ \
V п
__
x v-~- — см. [434], [863]:
v=lJS(xv)-Jf

Сопоставляя равенства (14.79) и (14.80), определяем искомые
коэффициенты A v':
J o(Xv)J1
A v' = к А р
>
R k
/ \
R t
X v R~
с ,J
У
0
X v R~
J
(14.81)
су
J2o(Xv)-J2{
Ri
С у
Подставляя найденное выражение коэффициента A v' в равен
ство (14.78), получаем окончательную формулу для определения
понижения давления в любой точке пласта в любой момент:
Ар (г, t) = Ар су
/0(*v)/l
г \
Rk
XvT~
s
__
- cl- W
r R k V v
*v-^-
2 Kt
e Kc
(14.82)
Легко проверить, что формула (14.82) удовлетворяет граничному
условию (14.4) на стенке скважины. Действительно, полагая г = Rc
в формуле (14.82) и учитывая, что ( jc v ) = 0, согласно соотно
шению (14.77), приходим к равенству:
ЛР {R су О А/? с у ,
(14.82а)
которое и выражает собой упомянутое граничное условие.
Полагая г = Rk в равенстве (14.76) и учитывая соотношение
(П. 162а), получим
R,
(14.83)
nxvRk*
Чтобы определить понижение давления Ар (Rht) на закрытой
границе пласта К в любой момент t, надо положить г = Rk в
формуле (14.82) и учесть соотношение (14.83):

Полагая t— из формул (14.82) и (14.84) легко обнаружить,
что
Следовательно, при t = °o во всем пласте понижение давления
должно стать равным понижению давления в скпажине, что является
естественным следствием условия замкнуто-упругого режима. Фор
мулы (14.82) и (14.84) впервые были выведены Херстом [868], а
все последующие в данном параграфе — Маскетом [434].
Определим расход жидкости Q(r,t) через боковую поверхность
цилиндра радиуса г в любой момент. Пользуясь формулой (14.29),
выражающей закон Дарси, и дифференцируя по г равенство (14.82),
получим
Чтобы определить дебит скважины, надо в последней формуле
принять,что г = Rc. Тогда, учитывая еще уравнение (14.74) и
соотношение (П. 162а), дебит скважины Qc(t) как функцию времени
можно записать так:
[Лр(г,0]<=» = Арсу; [Ар(Ль#)]<=„ = Арсу. (14.85)
(14.86)
r jU \ R )
v=lJl(xv)-J2i x v-j£ (14.86а)

Если принять, что г = Rb то выражение, заключенное в
квадратных скобках в формуле (14.86), обращается в нуль; поэтому
оказывается, что
Qk(Rbt) = О,
(14.87)
как это и должно быть согласно граничному условию на внешней
границе.
Кроме того, полагая t~>oo в формулах (14.86) и (14.86а),
обнаруживаем, что
[Q(r,01Г— = 0Э lQ(Rc,t) h=~ = 0.
(14.88)
Эти результаты, опять-таки, согласуются с условиями замкну
то-упругого режима.
Чтобы подсчитать количество (объем) жидкости V (г, t), которая
за время t перетечет через боковую поверхность цилиндра радиуса г,
следует проинтегрировать равенство (14.86) по времени в пределах
от 0 до t:
V(r cyRc
[X к
v=b
JQ{xv)Ji
Rk
Х V D
I ,
х V
H(XV)-J\
f RA
XvTc]
v J
R>
R.
xv
Rt
-J i
Y A xv
(14.89)
2 Kt \
1 -e
Заметим, что входящую в формулу (14.89) величину — можно
\i к
заменить через коэффициент упругоемкости пласта р * — см.
равенство (1.41).
Формула (14.89), как и формулы (14.82), (14.86), громоздкая и
неудобная для подсчетов. В последующих главах будут приведены
более удобные приближенные формулы.
Полагая г = Rc в формуле (14.89), можно определить количе
ство V с ( t ) жидкости, которое будет добыто из скважины за время t.
Однако проще проинтегрировать не столь громоздкую формулу
(14.86а):

t
^ло=1е<г(о^=4лл2ьэ*Арсух
где для коэффициента упругоемкости р * использовано выше уже
упоминавшееся соотношение (1.41).
Полагая в последней формуле t = «>, определяем объем жидко
сти, который может быть добыт из скважины за все время в
рассматриваемых условиях замкнуто-упругого режима:
Из физических соображений очевидно, что в условиях замкну
то-упругого режима из скважины будет добыто количество жид
кости, равное ее упругому запасу V ^ во всем объеме ограниченного
пласта при снижении давления во всех его точках на величину
А р су (ведь выше было отмечено, что при t = <*> понижение давления
во всем пласте будет равно понижению давления в скважине):
Сопоставляя две последние формулы, обнаруживаем, что
должно быть справедливо следующее равенство:
Этим подтверждается уже упоминавшееся в предыдущих главах
утверждение Рэлея о возможности косвенным путем, достаточно
г
\
(14.896)
[Vc(01/—= я(Я|-Л?)ЬР*Арсу = Уяи. (14.90)
/ \
Rj-Rl (14.90а)
ZTH 4Rc
Rc
\
